基于機器學習的再生混凝土配合比設計方法

劉凱華 ，鄭佳凱 ，謝維力 ，董書雄 ，段珍華

（1.廣東工業大學 土木與交通工程學院，廣東 廣州 510006；2.同濟大學 土木工程學院，上海 200092）

再生骨料具有吸水率高、表觀密度低和壓碎指標值大等特點.殘余漿體的存在使得再生混凝土內部存在多重界面過渡區［1］，導致其耐久性能較普通混凝土有所降低［2］.再生混凝土材料耐久性能直接影響再生混凝土結構的長期服役性能［3］.一般認為，再生混凝土抗氯離子滲透性能［4-5］和抗碳化性能［6］較普通混凝土要低，且隨著再生骨料取代率的提高逐漸下降.已有學者基于試驗結果發展了再生混凝土耐久性的預測模型［7-8］，但此類“機理驅動”的半經驗半理論模型精度尚有較大提升空間.近年來人工智能發展迅速，機器學習等技術的快速發展為再生混凝土耐久性預測問題的建模提供了新的思路.不同于“機理驅動”的傳統建模方法，“數據驅動”的機器學習建模方法能夠充分挖掘試驗數據中輸入和輸出的映射關系，建立精確的預測模型［9］.國內外學者已嘗試將機器學習應用于混凝土材料的研究之中，針對其抗壓強度［10-11］、彈性模量［12］和早期收縮［13］等性能預測開展研究，均取得了較為滿意的預測效果.

目前針對再生混凝土的配合比設計主要從強度角度出發，對其耐久性能要求則是以控制強度等級、水灰比等指標進行概念設計.為實現再生混凝土的性能可控，發展耦合強度和耐久性的配合比設計方法具有重要的工程意義.基于此，本文將機器學習方法引入再生混凝土的耐久性能研究，建立再生混凝土抗氯離子侵蝕性能和抗碳化性能預測的機器學習模型.將提出的再生混凝土耐久性預測模型和生產成本作為目標函數，利用設計強度確定配合比約束條件，結合多目標優化算法發展再生混凝土配合比優化設計方法.

1 機器學習算法

機器學習算法可分為有監督學習和無監督學習兩大類.有監督學習是對具有標簽的訓練樣本進行學習，以盡可能對訓練樣本集外的數據進行分類和回歸；無監督學習則是對沒有標簽的訓練樣本進行學習，主要為數據聚類和數據降維.本文采用了4 種有監督機器學習方法，包括2種單一學習方法和2種集成學習方法.

1.1 單一學習模型

1）反向傳播神經網絡（Backpropagation Artificial neural Network，BPANN）.BPANN 是一類基于誤差反向傳播算法的多層前饋神經網絡［14］，包含輸入層、隱藏層和輸出層.輸入層、隱藏層和輸出層中神經元通過權重和偏差依次連接.權重和偏差最初是隨機分配的，然后根據訓練過程的結果進行不斷優化.

2）高斯過程回歸（Gaussian Progress Regression，GPR）.GRP 是對輸入變量與輸出變量間的概率分布進行推斷，即給定輸入變量后確定輸出變量的條件分布［15］.與其他機器學習模型相比，GPR 結合了統計學習和貝葉斯理論，可以有原則地量化預測不確定性，適用于處理高維度和強非線性問題.

1.2 集成學習模型

1）隨機森林（Random Forest，RF）模型.RF 模型由多棵獨立的決策樹組合而成，每棵決策樹都是通過隨機方法生成的［16］.模型預測通過投票或平均每個決策樹的結果來確定.對回歸問題，RF 模型輸出結果F（x）可表示為：

式中：fi（x）代表第i棵決策樹的預測結果；T代表決策樹的數量.

2）梯度提升樹（Gradient Boosting Decision Tree，GBDT）模型.GBDT 模型以單一決策樹模型作為基學習器，模型的訓練過程即是可導出目標函數的優化過程［17］.GBDT 模型采用平方誤差作為損失函數，利用損失函數的負梯度作為擬合的目標值.對回歸問題，GBDT算法的計算過程如下：式中：G0代表初始基學習器；Gr代表輸出的強學習器；L代表損失函數；hr代表弱學習器；?Loss 代表損失函數的負梯度.

2 再生混凝土耐久性預測模型

2.1 數據集及預處理

分別采用電通量和碳化深度作為再生混凝土抗氯離子滲透和抗碳化性能量化指標.模型輸入變量考慮再生混凝土配合比、再生骨料品質、養護條件和侵蝕環境等層面的影響確定.針對氯離子侵蝕環境，考慮到電通量法試驗環境一致，因此將水泥用量（ρc）、水用量（ρw）、砂用量（ρs）、粉煤灰用量（ρfa）、骨料取代率（R）、骨料吸水率（Rwa）和齡期（A）等作為輸入變量.針對碳化環境，選取水泥用量（ρc）、水用量（ρw）、骨料取代率（R）、骨料吸水率（Rwa）、齡期（A）、二氧化碳體積分數（φCO2）、環境溫度（T）、環境濕度（RH）和碳化時長（tc）等作為輸入變量.骨料吸水率以再生骨料和天然骨料的吸水率根據骨料質量取代率加權后計算得到.

收集了200 組再生混凝土氯離子侵蝕試驗樣本［18-26］和502 組碳化試驗樣本［27-37］.樣本中再生混凝土制備工藝均為傳統工藝，粉煤灰類別均為低鈣型Ⅰ級粉煤灰.模型變量的統計特征值見表1.為避免輸入變量潛在共線性造成信息重復，采用方差膨脹因子（Variance Inflation Factor，VIF）法進行多重共線性分析.VIF 是自變量回歸系數估計量的方差與假設各自變量之間線性無關時方差的比值.VIF 值越大，則代表該自變量與其他自變量之間共線性越明顯，一般以10 作為判斷邊界.本文利用SPSS 軟件計算得到各輸入變量的VIF 值.從表1 可知，各自變量VIF 值均小于10，排除多重共線性，數據集可用于機器學習模型訓練.

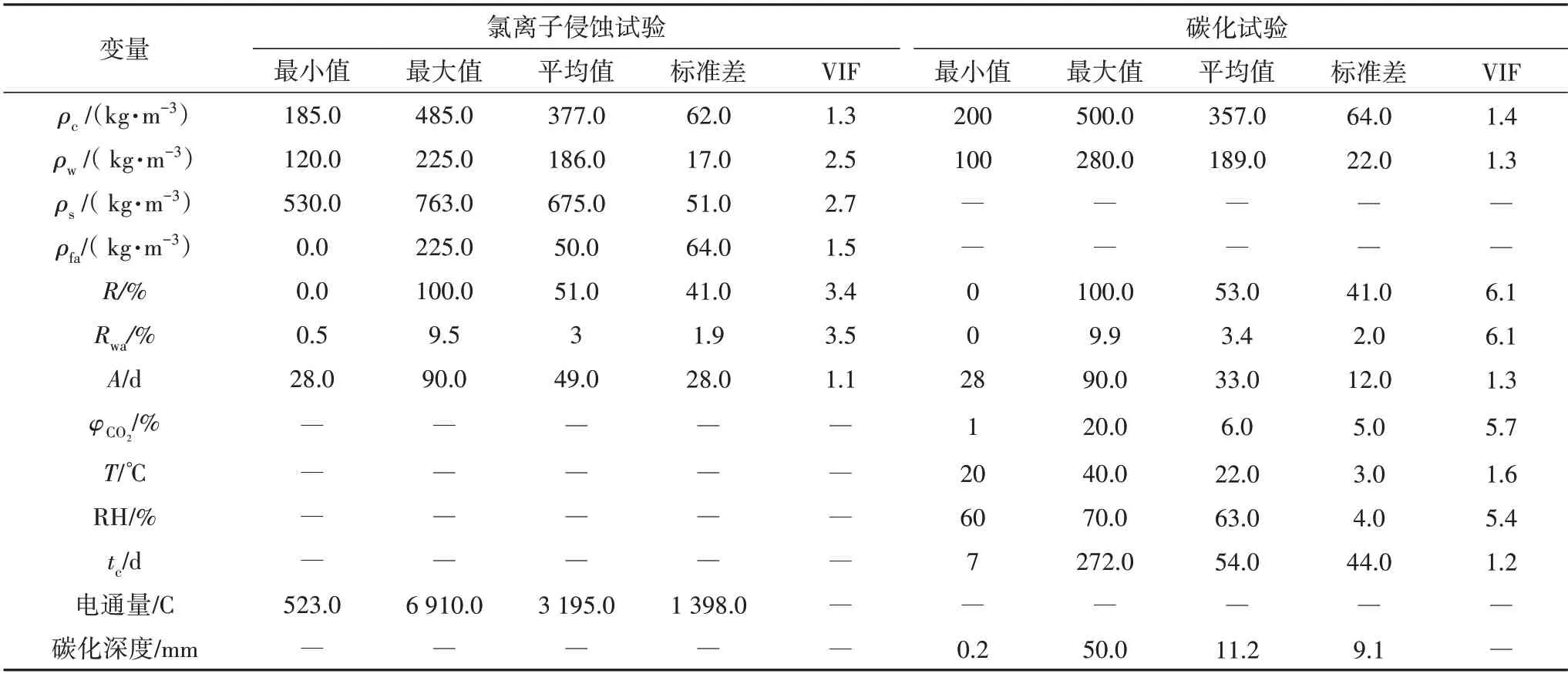
表1 模型變量的統計特征值Tab.1 Statistical indicators of model variables

2.2 模型訓練和超參數優化

將數據庫劃分為訓練集（80%）和測試集（20%），在MATLAB 平臺采用5 折交叉驗證訓練模型.訓練過程中需要針對模型超參數進行優化以提升模型性能.常見調參算法有網格搜索、隨機搜索和貝葉斯優化等［38］.網格搜索和隨機搜索不需要人力，但是優化效率低、耗時長.貝葉斯優化是基于目標函數過去評估結果建立概率模型，優化效率相對高，適用于參數維度不超過20 的機器學習模型.本文采用貝葉斯優化分別針對BPANN模型、GPR模型、RF模型和GBDT 模型的部分超參數進行優化，結果見表2.針對RF 和GBDT 模型，考慮到樣本特征數均在10 以內，因此將單個基學習器最大特征數和最大深度設置為自動獲取.

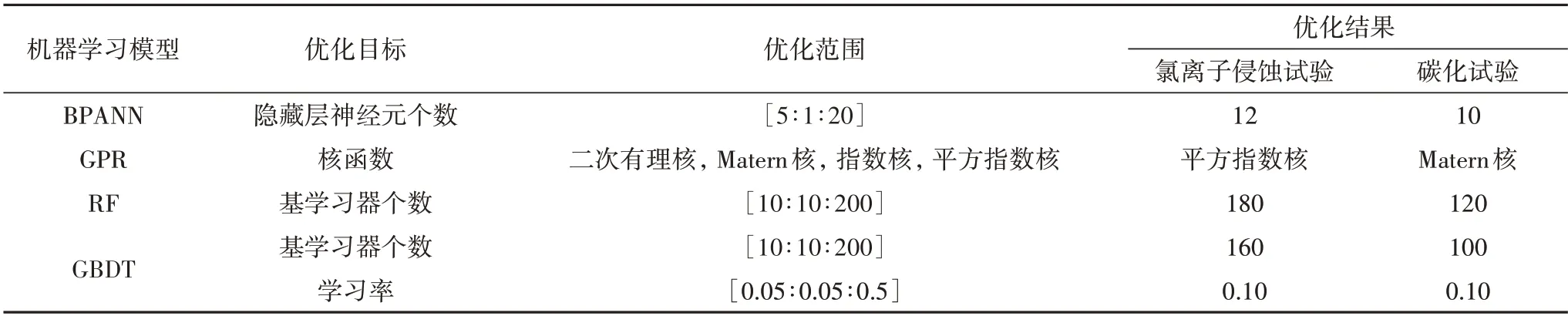
表2 機器學習模型超參數優化結果Tab.2 Optimization results of hyperparameters for machine learning models

2.3 模型性能評估

采用決定系數（R2）和均方根誤差（RMSE）評估機器學習模型的預測性能，計算公式如式（5）（6）：

式中：ft和fp分別代表試驗結果和預測結果和分別代表試驗結果平均值和預測結果平均值；N代表數據點的個數.

根據優化后的超參數可以分別建立再生混凝土電通量和碳化深度的機器學習預測模型.

圖1 給出了再生混凝土電通量預測值和試驗值的對比結果.從圖1（a）～（d）可看出，本文機器學習模型訓練集和測試集的R2都在0.95 以上、RMSE都在350 以下，表現出很高的預測精度.輸入變量各模型在測試集的表現較訓練集有所下降，但與試驗結果擬合良好，展現出良好的泛化能力.其中，GBDT 模型性能表現最好，R2在0.98 以上且RMSE在150 左右，其訓練集和測試集預測性能均高于其他模型；BPANN 模型和RF 模型性能比較接近，略低于GPR模型.為進一步驗證本文模型性能，根據陳正等［39］提出的電通量非線性回歸預測模型對數據集進行了預測.從圖1（e）可看出，非線性回歸模型精度相對偏低.其原因是一方面算法本身對數據特征的識別能力有區別，另一方面本文模型輸入變量除考慮配合比設計參數外，也考慮了再生骨料品質，提升了模型性能.

圖1 再生混凝土電通量預測值與試驗值的對比Fig.1 Comparison between the predicted and experimental electric flux of RAC

圖2 給出了各模型針對再生混凝土碳化深度預測值和試驗值的對比結果.圖2（a）～（d）表明，各機器學習模型在訓練集和測試集的R2都在0.93 以上、RMSE都在2.0 以下.其中，GPR 模型的預測性能最好，GBDT 模型次之但略高于RF 模型，BPANN 模型的預測性能則要低于其他模型.從圖2（e）可以看出，Zhang 等［7］提出的再生混凝土碳化深度預測模型在訓練集和測試集的R2分別為0.797和0.776，RMSE分別為3.9 和4.3，較本文采用的機器學習模型預測精度有所降低，進一步驗證了本文碳化深度機器學習預測模型的性能.

圖2 再生混凝土碳化深度預測值與試驗值的對比Fig.2 Comparison between the predicted and experimental carbonation depth of RAC

2.4 參數分析

在建立再生混凝土耐久性預測機器學習模型后，利用參數分析考察模型針對關鍵變量波動的變化趨勢，提高模型可解釋性.為獲得影響再生混凝土抗氯離子侵蝕和抗碳化性能關鍵參數，采用標準化回歸系數（Standardized Regression Coefficient，SRC）量化各輸入參數貢獻.SRC 是對輸入參數和輸出參數同時進行標準化處理后所得的回歸系數，其絕對值直接反映輸入參數對輸出參數的影響程度.圖3給出了各自變量SRC 計算結果.從圖3 可知，用水量是影響再生混凝土抗氯離子侵蝕的關鍵參數，其次是齡期；二氧化碳體積分數是影響再生混凝土抗碳化性能的最主要參數，其次為水泥用量.

圖3 SRC計算結果Fig.3 Calculation results of the SRC

以預測再生混凝土抗氯離子侵蝕和抗碳化性能表現最佳的GBDT 模型和GPR 模型開展關鍵參數分析.針對GBDT 模型，改變用水量和齡期，同時將其他變量取為數據集平均值；針對GPR模型，以水泥用量和二氧化碳體積分數為自變量，同時保持其他變量為數據集平均值，觀察模型輸出結果.從圖4（a）可以看出，隨著用水量增加，電通量逐漸增大，在用水量超過160 kg/m3后快速增加.用水量增加會增大再生混凝土水灰比，降低漿體密實度，對抗氯離子侵蝕不利.隨著齡期增加，電通量逐漸降低，在齡期超過70 d 后，電通量降幅很小，基本不變.齡期增加會使得水泥水化更加充分，增強再生混凝土密實性，提高抗氯離子滲透性［5］.當齡期達到一定時間后，水化過程已比較充分，此時繼續延長齡期帶來的性能提升也有所放緩.從圖4（b）可知，提高水泥用量可以降低碳化深度，當水泥用量超過400 kg/m3時，繼續增加水泥用量對再生混凝土抗碳化性能的提升效果已不再顯著.增加環境中二氧化碳體積分數則會逐漸增大再生混凝土的碳化深度，這與已有研究結果是一致的［6］.

圖4 參數分析結果Fig.4 Results of the parameter analysis

3 再生混凝土配合比優化設計方法

3.1 設計流程

本文將提出的再生混凝土耐久性預測模型作為目標函數，結合設計強度要求確定配合比各項因素約束條件，利用 NSGA-Ⅱ算法進行多目標尋優獲得Pareto最優解集合，然后對最優解集合進行綜合評價排序，獲得最佳配合比組合.

3.2 設計案例

以廣州市某高速鐵路建設項目再生混凝土配合比設計為例.本項目要求再生混凝土配置強度為35 MPa，標準養護28 d 試件電通量和28 d 碳化深度（依規范試驗方法［40］）分別不超過1 500 C 和5 mm，成本在500 元/m3以下.選用P.O 42.5 水泥（28 d 膠砂抗壓強度49.5 MPa），I 級粉煤灰（摻量10%），再生粗骨料吸水率5.0%，天然碎石吸水率0.5%，再生粗骨料取代率為50%.各原材料的選用符合規范要求［41］，各組分的表觀密度和價格見表3.

表3 材料信息Tab.3 Information of materials

本工程再生混凝土配合比優化設計過程如下：

1）確定目標函數.將建立的再生混凝土電通量預測模型和碳化深度預測模型及每立方米再生混凝土成本作為目標函數，設定各目標函數數值：

式中：x1、x2、x3、x4、x5分別為水泥用量、凈水用量、砂用量、再生粗骨料用量、天然粗骨料用量等變量；con1、con2分別為養護齡期、骨料吸水率；con3、con4、con5、con6分別代表標準加速碳化試驗參數中的二氧化碳體積分數、環境溫度、環境濕度和碳化時長等已知量.

2）構建約束條件.采用郭遠新等［42］提出的再生粗骨料混凝土抗壓強度計算公式，換算得到再生混凝土的設計水膠比rW/C不超過0.55.根據規范［41］要求并結合工程實際，將砂率控制在35%～40%，膠凝材料總量不低于300 kg/m3，各變量具體約束范圍如下：300 ≤x1≤450，0.35 ≤x2/()1.1x1≤0.55，1 000 ≤x4+x5≤1 300，0.35 ≤x3/()x3+x4+x5≤0.40，各材料體積之和為1 m3（含氣量設定為1%）.

3）尋找配合比最優解.在確定目標函數和約束條件后，采用NSGA-Ⅱ算法進行多目標尋優.NSGA-II 算法主要參數設置為：種群數量100，迭代次數500，交叉概率0.9，變異概率0.1.利用熵權法確定優化指標電通量、碳化深度和成本的權值系數依次為0.422、0.415 和0.162.采用優劣解距離法（Technique for Order Preference by Similarity to Ideal Solution，TOPSIS）作為綜合評價方法計算每個指標與理想解和負理想解的距離，對最優解集進行排序.再生混凝土電通量、碳化深度和成本等優化目標越小越好，其理想解和負理想解可表示為：

Pareto 解集中的每組解與理想解和負理想解之間的距離可采用歐氏距離進行計算：

每組解與相對理想解的接近程度可定義為：

式中：Ci為第i組解的相對接近度系數，其數值越大，表明該組解越優.

根據Ci對Pareto 解集進行排序確定本項目試配配合比：水185 kg/m3（凈用水和附加水之和［41］），水泥410 kg/m3，河砂600 kg/m3，再生粗骨料530 kg/m3，天然粗骨料585 kg/m3，粉煤灰40 kg/m3.

4）試驗驗證.經測定，該試配配合比制備的標準養護28 d再生混凝土試件棱柱體抗壓強度平均值為37.2 MPa，電通量和28 d 碳化深度分別為1 215 C 和3.7 mm，滿足設計要求且成本可控，可作為本工程項目的施工配合比.

4 結論

1）本文建立的機器學習模型可以較好地預測再生混凝土抗氯離子侵蝕和抗碳化性能.梯度提升樹模型在預測再生混凝土電通量時表現最好，模型決定系數0.989，均方根誤差147.3；高斯過程回歸模型對再生混凝土碳化深度預測性能要優于其他模型，模型決定系數0.987，均方根誤差1.0.

2）變量標準化回歸系數分析表明，用水量是影響再生混凝土抗氯離子侵蝕的關鍵參數，其次是齡期；二氧化碳體積分數則是影響再生混凝土抗碳化性能的最主要參數，其次為水泥用量.梯度提升樹模型和高斯過程回歸模型針對關鍵變量波動的變化趨勢與已有試驗結果是一致的，驗證了本文再生混凝土耐久性預測機器學習模型的魯棒性.

3）結合再生混凝土耐久性預測機器學習模型和NSGA-Ⅱ多目標優化算法提出了再生混凝土配合比優化設計方法.該設計方法優化結果符合工程實際要求，顯示出良好的工程應用潛力，可用于指導再生混凝土的施工配合比設計.