基于DDPM模型的高壓管匯沖蝕磨損數值模擬

黃華寶, 錢玉寶, 郭旭濤, 余米森, 曹新建

(長江大學機械工程學院, 荊州 434023)

近年來,隨著石油勘探難度的不斷提升,采用了大排量、大馬力、高壓的水力壓裂設備[1-2]。高壓管匯不僅在高內壓下工作,且固體顆粒混合在壓裂液中,在這些惡劣的工作條件下,高壓管匯很容易失效或降低壽命,如管道彎頭、管壁狹窄等都容易受到這種類型的沖蝕[3]。沖蝕磨損是高壓管匯失效的最重要因素之一,所以對其沖蝕規律進行研究十分必要。

計算流體力學的發展給了沖蝕磨損計算新的嘗試,Liu等[4]提出了一種基于計算流體動力學(computational fluid dynamics,CFD)的簡化方法來計算環形流動彎頭的沖蝕速率,這種方法克服了目前半經驗模型的缺點,但僅在較大曲率半徑的彎管時,預測和實驗結果才具有較好一致性;Zhang等[5]通過單向耦合離散相模型(discrete phase model,DPM)討論了在高應力下壓裂液速度、流動方向和彎頭角度對高壓管匯沖蝕磨損位置的影響,但是沒有考慮到顆粒流體的相互作用;莫麗等[6]用計算流體動力學-離散相(computational fluid dynamics-discrete phase model,CFD-DPM)方法對流速、粒徑和空間夾角對異面三通沖蝕磨損性能影響進行分析,得出異面三通交匯處是磨損主要位置的結論,其分析前提是忽略顆粒間碰撞、平移;祝效華等[7]在忽略固相顆粒之間的碰撞以及粒子運動對流場的影響的前提下,建立了Y形和岐型三通沖蝕磨損計算模型,分析了空間夾角、質量流量、粒徑和支撐劑密度對Y形和岐型三通沖蝕磨損的影響,得出主支管交匯處是磨損最嚴重區域的結論;馮志成等[8]研究了流速、粒徑、質量流量和黏度對不同結構下Y形三通在的沖蝕影響規律,但沒有考慮離散相和連續相的耦合作用;Messa等[9]以歐拉-歐拉法為前提,首次提出了混合顆粒流的方法,使用的是歐拉-歐拉-拉格朗日法,即稠密離散相(dense discrete phase model,DDPM)模型;文獻[10]已證實,四相耦合的DDPM模型在彎管沖蝕中模擬顆粒軌跡上要好于DPM模型,但是其結果是否適用于高壓管匯岐型三通仍有待進一步研究。

綜上所述,目前高壓管匯沖蝕磨損理論研究大多數都是CFD-DPM模型,忽視了顆粒間碰撞平移作用的影響,隨著目前中高滲透油井的不斷增多,對支撐劑性能要求更高,而優質性能的壓裂液固相顆粒占比也更多,其中瓜膠壓裂液攜砂性能好且其固相顆粒占比可達到20%,因此在高壓管匯沖蝕磨損機理的研究中,需要考慮顆粒間和流體間的相互作用的影響。

現以高壓管匯岐型三通為研究對象,通過DDPM模型,對不同工況、顆粒物理特性和不同空間夾角的岐型三通數值模擬,來預測高壓管匯沖蝕磨損對使用壽命影響,為高壓管匯結構優化和剩余服役壽命預測提供理論指導。

1 理論模型

1.1 DDPM模型

DDPM模型在固定的歐拉網格上建立連續相位,基于歐拉-拉格朗日方法來追蹤顆粒。該模型考慮了粒子的空隙比和碰撞,用碰撞計算代替軟球模型計算碰撞過程。粒子之間的碰撞由顆粒流力學理論描述,連續性方程和動量方程如下。

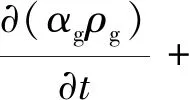
(1)

(2)

使用Realizablek-ε模型,在網格質量充足的情況下,具有更高的計算精度。湍流動能k和耗散率ε用微分方程[11]計算如下。

(3)

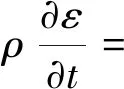
(4)

式中:γ為運動黏度系數;μt為湍流黏度系數;Xn為源項分量;C1ε、C2為湍流模型常系數;σk、σt為k方程和ε方程的湍流普朗特數,默認C1ε=1.44,C2=1.9,σk=1.0,σt=1.2;Sk和Sε為湍動能源項和湍流耗散源項;Gk為速度引起的湍流動能;Gb為浮力引起的湍流動能;γM為湍流脈動對總耗散率的影響;C3ε為影響浮力的不定常數;C1為方程修正系數。

質點運動軌跡由作用在質點上力的平衡方程來計算。質點在笛卡爾坐標系下的運動方程為

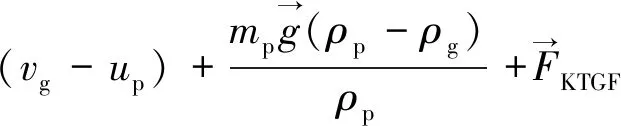
(5)

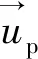
Rosin-Rammler分布函數長期以來一直被用來描述各種類型和大小的粒子的尺寸分布,更符合粒子運動情況。本文研究采用雙R分布,表達式為

(6)

式(6)中:Wp為保留質量分數,%;n為雙R分布偏態系數;D為實際粒徑;De為等效平均粒徑;本文中De∈[200,400] μm。

DDPM模型考慮四相耦合,在浮力、壓力梯度力、拖曳力同DPM耦合的基礎上,更考慮了顆粒流動力學理論,增加了顆粒間碰撞、平移等作用。

1.2 沖蝕計算模型

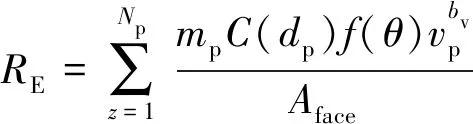
(7)

式(7)中:RE為沖蝕速率,kg/(m2·s);mp為質量流量,kg/s;C(dp)為顆徑函數,C(dp)=1.8×e-9;f(θ)為沖擊角函數,如表1所示;vp為顆粒流速,m/s;bv為顆粒速度方程,取bv=2.6;Aface為沖蝕區域面積,m2。

表1 沖擊角函數

壁面碰撞恢復方程[12]為

εn=0.993-0.030 7α+4.75×10-4α2-

2.61×10-6α3

(8)

ετ=0.988-0.029α+6.43×10-4α2-

3.56×10-6α3

(9)

式中:α為顆粒沖擊角;εn為法向壁面函數;ετ為切向壁面函數。

2 高壓管匯幾何模型

2.1 計算模型建立

在壓裂現場,高壓管匯主要包含Y形三通、歧型三通和U形彎管,其中歧型三通在整個高壓管匯中是承上啟下的作用,來自壓裂液的電化學腐蝕和固液兩相流的沖擊對高壓管匯壁面磨損非常嚴重,極易發生失效,現場高壓管匯沖蝕磨損,如圖1所示。

圖1 現場高壓管匯沖蝕磨損

選取高壓管匯內徑D=76 mm,為盡可能降低出入口端面效應的干涉,保證流域內流場穩定,選取流入段和流出段長度為均L=5D,高壓管匯幾何結構模型如圖2所示。

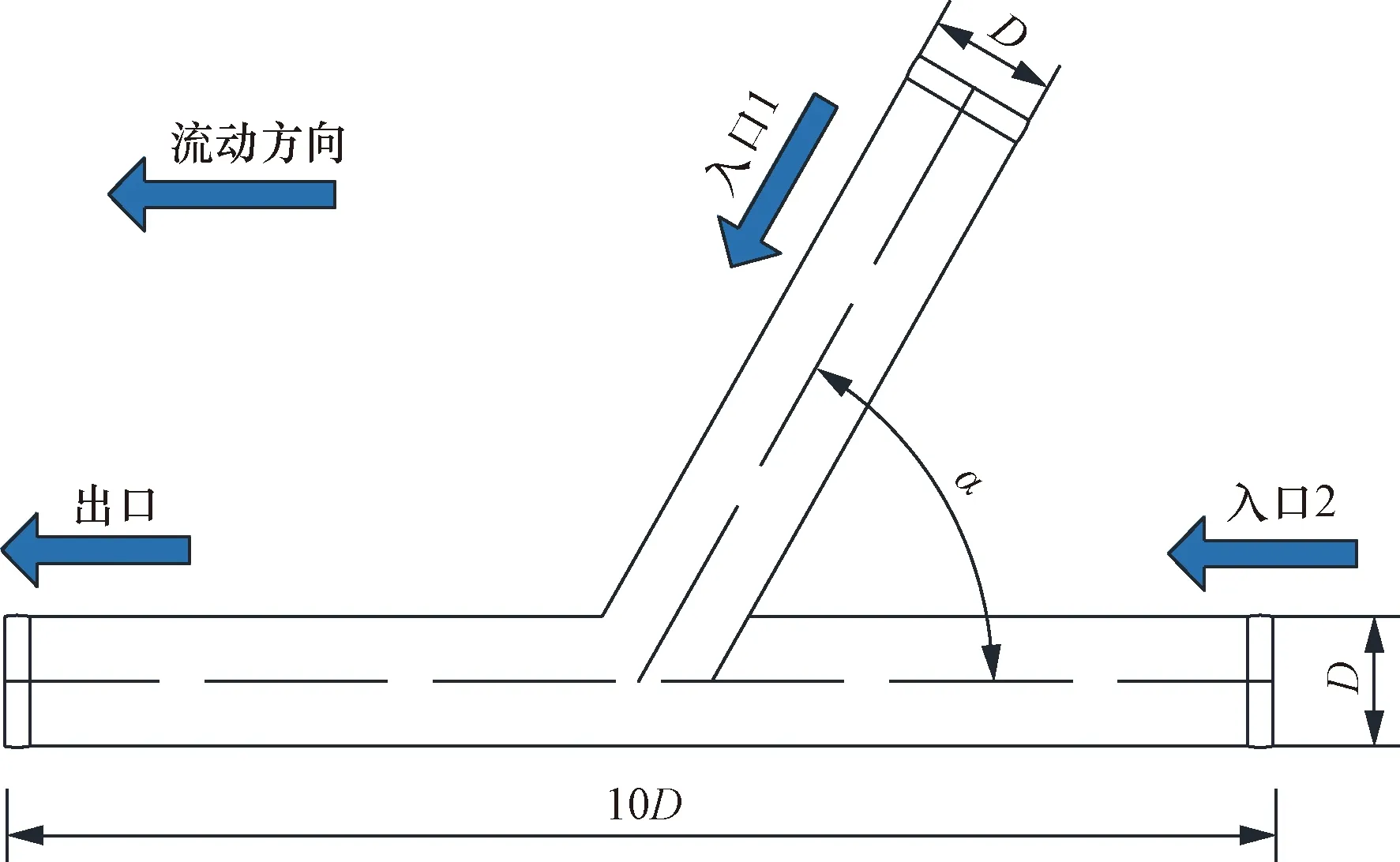
圖2 高壓管匯結構模型

2.2 網格劃分及邊界條件設定

根據岐型三通的結構參數,通過三維建模軟件分別建立岐型管匯幾何模型,導入Fluent中形成流域,在IECM中用O形剖切對流域進行結構化網格劃分,其中,高壓管匯岐型三通夾角α=60°時網格劃分如圖3所示,網格均采用結構化網格且通過無關性驗證。

圖3 網格劃分

在現場壓裂過程中,岐型三通支管和壓裂車連接,流體流動可近似為速度一定,參考現場壓裂參數指標,設定支撐劑密度為2 700 kg/m3,黏度為30 mPa·s,連續相為非牛頓流體且不具有壓縮性,仿真邊界設定岐型主支管入口均為速度入口,出口設定為壓力出口,壁面無滑移,離散相物理參數和流體參數設置等和岐型主管保持一致。

3 數值模擬結果與分析

3.1 DDPM模型對岐型三通數值模擬

結合現場工況參數,如表2所示,用DDPM模型對高壓管匯進行數值模擬,對岐型三管的空間夾角一共設置5組,分別是α=30°、45°、60°、75°、90°,研究不同結構參數對高壓管匯沖蝕速率和沖蝕區域的影響。

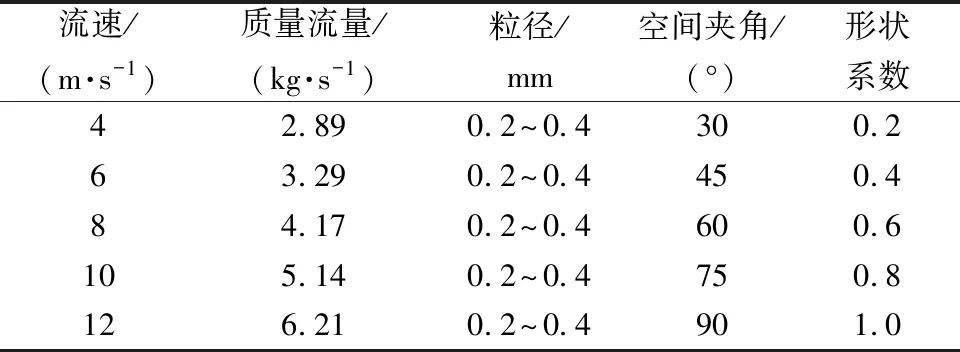
表2 工況條件參數

在工況流速為10 m/s,空間夾角α=60°下仿真結果如圖4所示;由圖4(a)和圖4(b)壓力速度云圖可知,在歧型三通主分管交匯區,可較明顯看出流動分層,結合流體力學可知,三通主分管交匯處流入段壓力小于流出段,形成一個二次流動閉環區域。

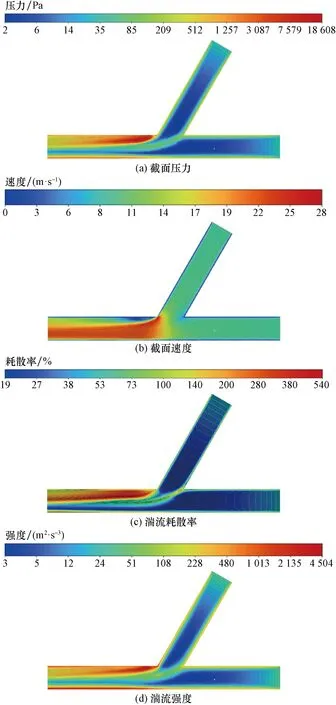
圖4 仿真云圖

由圖4(c)和圖4(d)可知,岐型三通交匯區域靠近出口內壁上部的湍動能和湍流耗散率呈現增大趨勢,側面體現了流體在流動過程中出現拐點,形成小范圍的二次流動。

3.2 工況參數對沖蝕的影響

通過DDPM和DPM模型,對岐型三通開展正交試驗,以研究工況參數對不同結構參數高壓管匯沖蝕速率的影響,其中包含5種工況和5種空間夾角,仿真得25組數值模擬結果,曲線圖如圖5所示。

圖5 DPM和DDPM模型下高壓岐型管匯沖蝕磨損數值模擬

通過對比分析可知,隨著工況變得劇烈,在兩種模型下高壓管匯沖蝕磨損均越來越嚴重。由圖5(a)可知:DPM模型中,隨著空間夾角的增大,沖蝕速率呈先增后減的趨勢,在空間夾角30°～45°和75°～90°時,不同工況參數下沖蝕速率相對較小,這可能是DPM模型計算主要圍繞流體運動軌跡,而隨著流體交匯處越來越充分,顆粒在接近壁面的區域不會出現大速度的匯聚產生沖擊,一定程度上反映出DPM模型忽略了顆粒間的相互作用。

由圖5(b)知:DDPM模型中隨著空間夾角的增大,沖蝕速率也是先增后減,但在30°～45°和75°～90°時的不同工況下沖蝕速率體現更明顯,這一定程度體現了DPM模型忽略了離散相間相互碰撞作用,尤其當顆粒體積分數較高時會有一定的偏差,而DDPM模型體現相對更完整更接近流體的實際流動。

3.3 空間夾角對沖蝕的影響

為繼續探究空間夾角對高壓管匯沖蝕磨損機理的影響,在流速和流量最大的工況下,對比分析高壓管匯沖蝕云圖,如圖6所示。

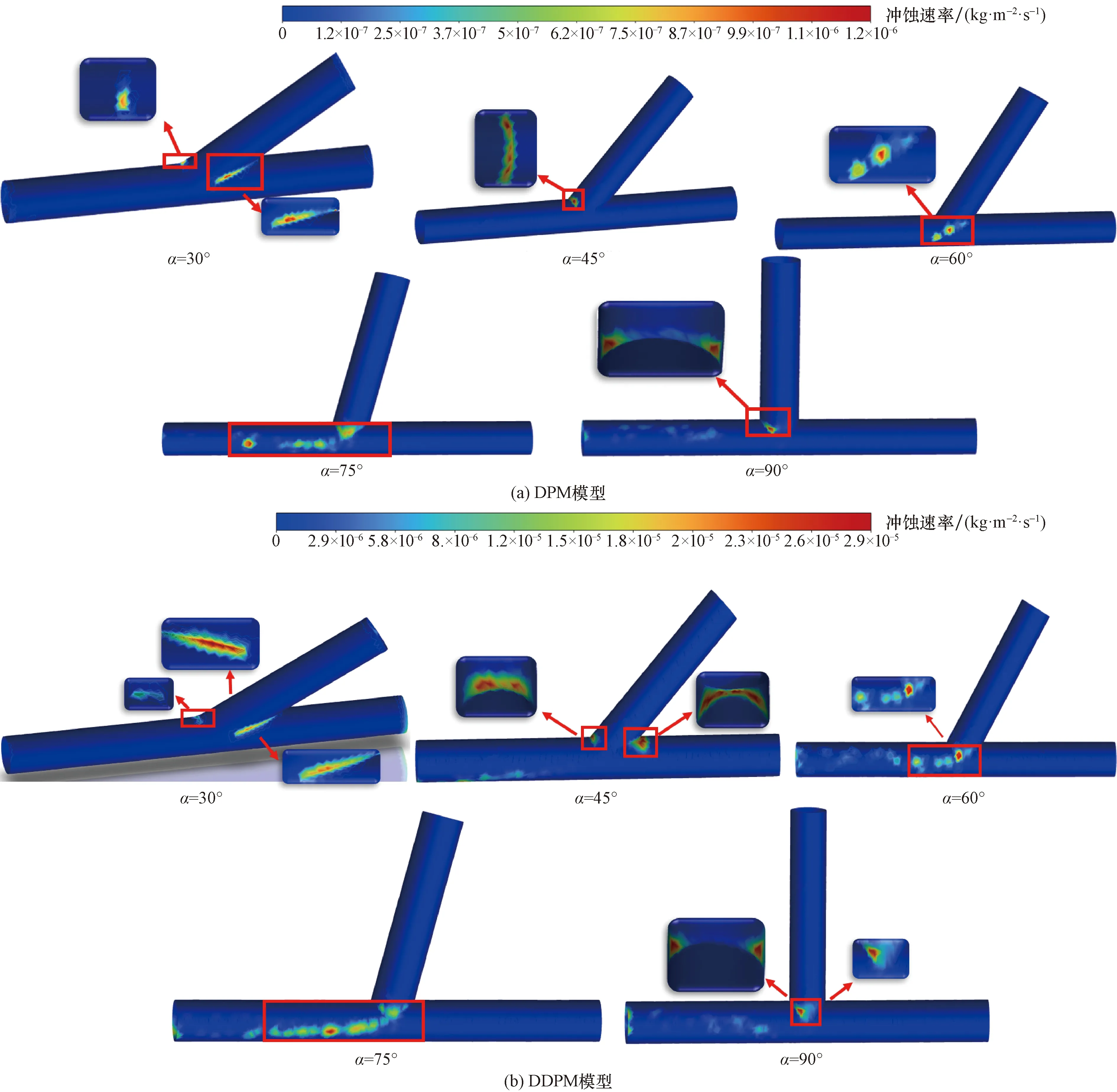
圖6 不同模型下沖蝕云圖對比

在DDPM和DPM兩種模型下,空間夾角為30°和45°時,沖蝕區域集中在岐型三通相貫線處,沖蝕面積較小,原因可能是空間夾角比較小時,因三通結構的改變,壓裂液經過流體交匯處,相間沖擊變大,更易沖蝕相貫線處壁面。空間夾角逐漸變大時,流體交匯處方向改變相對變大,產生的慣性更大,沖蝕磨損區域集中在相貫線及其兩側壁面,空間夾角增大為90°時,沖蝕區域相對變小,主要集中在岐型三通相貫線處。

DDPM模型考慮四相耦合,在浮力、壓力梯度力、拖曳力同DPM耦合的基礎上,更考慮了顆粒流動力學理論,增加了顆粒間碰撞、平移等作用。在相同結構參數下,DDPM模型沖蝕速率和沖蝕區域相對更明顯可能是顆粒較多的聚集,相互碰撞導致沖蝕磨損嚴重。

3.4 顆粒軌跡對沖蝕影響

在流速為8 m/s,質量流量為4.17 kg/s,不同結構參數的顆粒軌跡如圖7所示,容易形成沖蝕的區域主要為歧型三通相貫線和出口主管軸線側壁。

圖7 顆粒軌跡

由圖7可知,在高壓管匯歧型三通相貫線和出口處主管軸線側壁存在顆粒軌跡的交匯,原因可能是流體在相貫線交匯時存在局部水力損失,三通主分管交匯處流入段壓力小于流出段,靠近交匯處外壁內側形成流速較小范圍的二次流動,此時由于離心力影響,顆粒間相互碰撞概率變大,相貫線區域沖蝕壁面加劇。

3.5 顆粒形狀對沖蝕影響

為研究高壓管匯沖蝕磨損規律,引入顆粒物理特性進行分析,在不同流速下,取顆粒形狀系數分別為0.2、0.4、0.6、0.8和1來分析形狀系數對高壓管匯沖蝕速率的影響,結果如圖8所示。隨著形狀系數減小,管匯最大沖蝕速率變大,加重了沖蝕磨損。

圖8 形狀系數對沖蝕的影響

由圖8可知,隨著顆粒逐漸變得尖銳,最大沖蝕速率從3.875×10-5kg/(m2·s)增大到5.436×10-5kg/(m2·s),變大1.4倍,隨著流速從4 m/s增加到12 m/s,沖蝕速率逐漸增大,并在流速最大時達到峰值。圖8中可以發現,在流速6～8 m/s和10～12 m/s時,沖蝕速率上升幅度較小,可能是此時主管和支管顆粒速度和流體速度變化不大,形狀系數小但是曳力系數大,顆粒流體相互作用更溫和,離散相和連續相跟隨性較好,從而降低碰撞壁面的概率,減緩了沖蝕。

4 結論

(1)歧型三通結構參數α=60°～90°時,最大沖蝕集中在三通相貫線和相貫線兩側面;在α=30°～45°,沖蝕集中在三通相貫線處,結果同現場高壓管匯沖蝕磨損區域相對應,佐證仿真結果合理性,可為今后高壓管匯結構優化提供借鑒意義。

(2)歧型三通沖蝕磨損危險區主要集中在相貫線處,可選擇最大沖蝕速率的一半作為確定該危險區域的標準,隨著范圍的縮小,現場監測時,可更好地對該區域厚度檢查。

(3)現場工況下,岐型三通主支管交匯區會存在顆粒匯聚,體積分數甚至超過15%,DDPM模型在DPM模型基礎上增加了顆粒間相互作用力,顆粒軌跡更符合實際流體流動,因此,在用CFD方法對高壓管匯進行沖蝕磨損數值模擬時,必須考慮顆粒間相互作用力和連續相和離散相間作用力。