活躍在2023年高考卷中的“爪形”三角形
安徽省蕪湖市第一中學(241000) 劉海濤 張大偉
《普通高中數學課程標準(2017 年版2020 年修訂)》(下稱《課程標準》)指出[1]:“通過高中數學課程的學習,學生能獲得進一步學習以及未來發展所必需的數學基礎知識、基本技能、基本思想、基本活動經驗(簡稱‘四基’);提高從數學角度發現和提出問題的能力、分析和解決問題的能力(簡稱‘四能’).”梳理2023 年高考數學卷, 有這樣一類解三角形問題,連接已知三角的一個頂點與其對邊的任一點,構成“爪形”結構的圖形,求解該類三角形的邊、角、面積等. 這類問題能有效考查學生的直觀想象、邏輯推理、數學運算、數據分析等數學核心素養,既有對解三角形基本知識、基本思想方法的考查,也有融合向量、解析幾何等知識的考查,體現了高考的基礎性、綜合性、創新性的考查要求,具體如下表1. 由于解三角形知識的本身特性,近五年的高考中尚未考查其應用性.
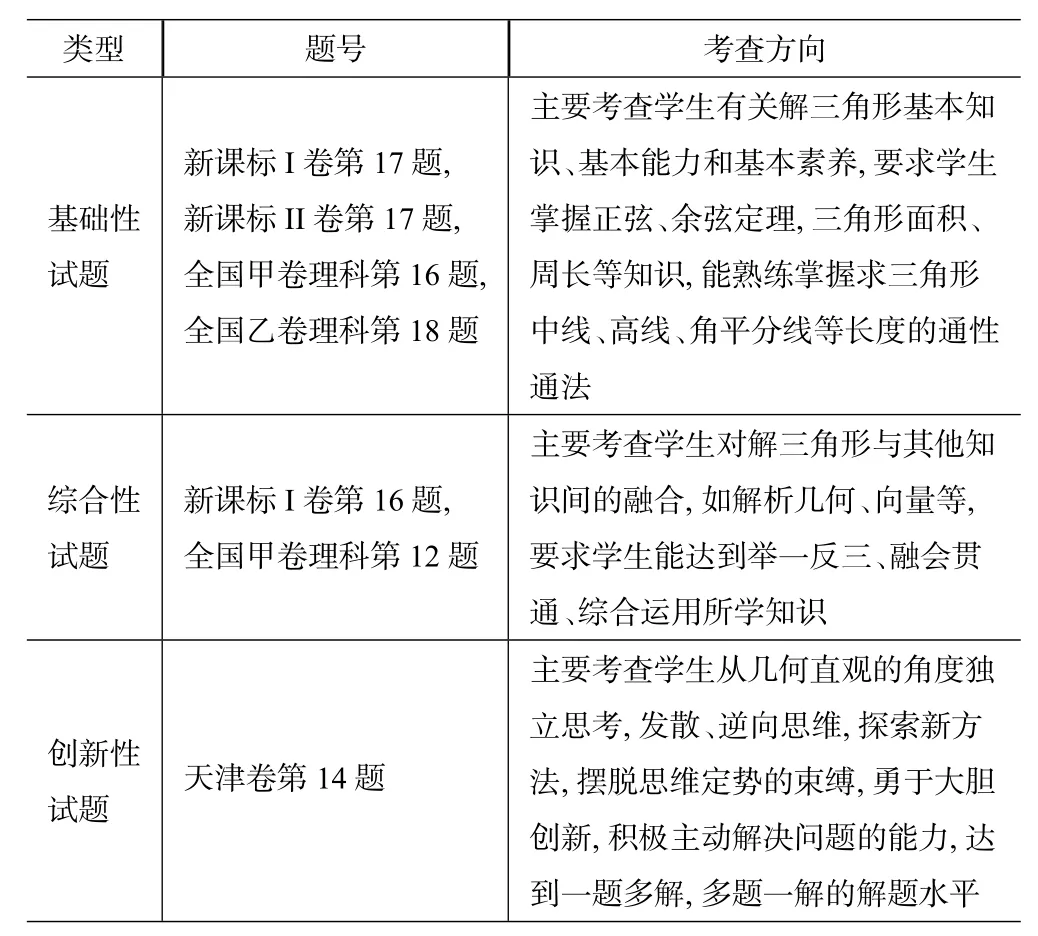
表1: 2023 年高考“爪形”三角形試題分類
1 有關“爪形”三角形的性質
如圖1 所示, 在?ABC中, 角A,B,C的對邊分別為a,b,c,D為BC上一點. 則有如下性質:
性質1
性質2(張角定理)
證明由S?ABD+S?CBD=S?ABC,得
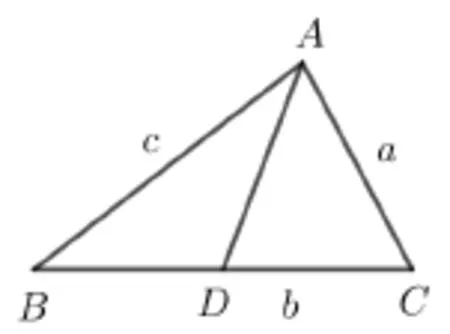
圖1
性質3(斯特瓦爾特定理)
證法1在?ABD和?CBD中, 由余弦定理, 得c2=AD2+BD2-2AD·BD·cos ∠ADB,a2=CD2+BD2-2CD·BD·cos ∠CDB,注意到∠ADB+∠CDB=π,則
特別地, 當BD為中線時, 有則
當BD為∠ABC的角平分線時, 有得a·AD=c·CD,則
2 部分試題分析
2.1 立足基礎,考查通性通法
《中國高考評價體系》指出:高考圍繞學科主干內容,加強對基本概念、基本思想的考查,杜絕偏難怪題和繁難試題,引動教學重視教材,夯實學生學習基礎,給學生提供深度學習和思考的空間[2]. 2023 年高考“爪形”三角形試題,主要考查學生有關解三角形基本知識、基本思想方法,要求學生掌握正弦、余弦定理,三角形面積、周長等知識,如新課標I 卷第17 題,新課標II 卷17 題,全國甲卷理科第16 題,全國乙卷理科第18 題等,這四道試題均來源于教材的例、習題的改編,只要學生基礎扎實,熟練掌握求三角形中線、高線、角平分線等長度的通性通法,考場中便可輕松解題.
例1(新課標全國Ⅱ卷)記?ABC的內角A,B,C的對邊分別為a,b,c,已知?ABC的面積為D為BC中點,且AD=1.
(2)若b2+c2=8,求b,c.
解析(1) 的解法1 在?ADC中,得a= 4. 在?ABD中,由余弦定理, 得cos ∠ADB= 7, 則又因為B為銳角, 所以tanB=
(1) 的解法2 同法1, 得a= 4, 由余弦定理, 得b2=CD2+AD2-2CD·AD·cos ∠ADC=3,得注意到AC2+AD2=DC2,得如√圖2 所示,過A作AE⊥BC于點E,于√是則
(2) 在?ABC中, 由D為BC中點, 且AD= 1, 得由即∠ADC=于是得b=c=2.
評注該題屬于中等難度試題,解題的關鍵在于熟練運用余弦定理、三角形面積公式等處理三角形中的邊角關系,對于“爪形”三角形中的中線,能夠熟記公式并運用,該題有效考查了學生的直觀想象、邏輯推理、數學運算等數學核心素養.
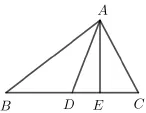
圖2
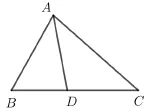
圖3
例2(甲卷理科第16 題)在?ABC中,∠BAC= 60?,的角平分線交BC于D, 則AD=____.
解法1如圖3 所示, 由余弦定理, 得AB2+AC2-由張角定理,得則AD=2.
解法2同法1, 得AC= 1 +3. 由正弦定理,得則在?ABD中,∠ADB=75?,所以AD=AB=2.
評注該題作為填空壓軸題,有一定難度,對于“爪形”三角形的角平分線問題,既可以利用三角形的面積公式解決角平分線問題,也可以用角平分定義結合正弦定理、余弦定理求解.
2.2 注重綜合,考查知識的融會貫通
《中國高考評價體系》指出:素質教育是內涵豐富的全面發展教育. 高考要求學生能夠觸類旁通、融會貫通,既包括同一層面、橫向的交互融合,也包括不同層面之間、縱向的融會貫通[2]. 2023 年的高考數學卷中,新課標I 卷第16 題和全國甲卷理科第12 題分別以雙曲線和橢圓為背景考查“爪形”三角形,考查了圓錐曲線的基本幾何性質、解三角形等相關知識,需要考生能夠將解析幾何與三角形等知識融會貫通起來,屬于難度較大的綜合性試題.
例3(新課標I 卷第16 題)已知雙曲線C:1(a,b>0)的左、右焦點分別為F1,F2. 點A在C上,點B在y軸上,則C的離心率為____.
解法1如圖4 所示,設B(0,m),由得
則m2= 4c2. 由點A在C上, 得結合b2=c2-a2整理得25c4-50a2c2+9a4=0,得5c2=9a2或5c2=a2(舍),所以
解法2設|BF1|=|BF2|=x, 則即得
評注該題是一道解析幾何與解三角形的綜合性問題, 關鍵在于構造出關于a與c的齊次方程式, 注意到|F1F2|= 2c, 且F2為?F1AB邊AB上的一定比分點, 故根據題意用a表示?F1AB的各邊長, 再利用便可輕松解題.
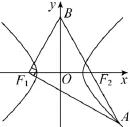
圖4
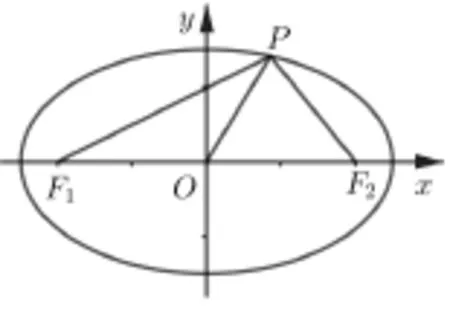
圖5
例4 (甲卷理科第12 題) 已設O為坐標原點,F1,F2為橢圓C:的兩個焦點, 點P在C上,
解法1如圖5 所示, 設P(x0,y0), ∠F1PF2= 2θ. 由所以故選B.
解法2在?PF1F2中,由余弦定理,得
結合2|PF1||PF2|= (|PF1|+|PF2|)2-|PF1|2-|PF2|2,由O為F1F2中點, 得|OP|2=故選B.
評注該題是壓軸選擇題,具有一定的綜合性,屬于中等偏難試題. 該題根據求解的目標可以選擇利用橢圓中的二級結論焦點三角形的面積公式快速解出,也可以常規利用定義結合余弦定理,再直接利用“爪形”三角形中線長公式解決.
2.3 強調創新,考查思維的靈活性
《中國高考評價體系》指出: 素質教育中的智育和以往教育理念中的智育最大的不同,在于其對創新性的強調[2].通過命題創新,創設新穎的試題情境、新穎的題目條件、新穎的設問方式,考查考生學生思維的靈活性與創造性. 2023 年高考的天津卷第14 題,雖是“爪形”三角形問題,卻沒有設問解三角形,而是將問題設置為求向量數量積的最大值,需要考生借助向量來“翻譯”題中的各個“爪形”三角形,最終將問題轉化為函數的最大值問題,有效考查學生思維的靈活性與創新性.
例5(天津卷第14 題)在?ABC中,∠A= 60?,BC=1, 點D為AB的中點, 點E為CD的中點,若設可用a,b表示為____;若則的最大值為____.
解析如圖6 所示, 由題知
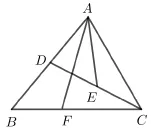
圖6
設|a|=p,|b|=q, 則在?ABC中, 由余弦定理, 得AB2+AC2-BC2=2AB·AC·cosA,即p2+q2=1+pq.由p2+q2≥2pq,得pq≤1(當且僅當p=q= 1 時取等號).由
于是當p=q=1 時取最大值,為
評注該題中共蘊含了三個“爪形”三角形,但題目并未設問求相關長度問題,而是以一個不定三角形為背景,以向量的形式來考查學生對三角形、向量、不等式、函數等知識,屬于一道創新性試題,能夠有效考查學生的思維的靈活性與創新性.
3 高考備考
高考試題是命題者在《課程標準》和《中國高考評價體系》的指導下, 經過反復醞釀、打磨、斟酌而成, 對高考的備考具有導向性與啟示性[3]. 因此,作為一線教師,應該善于從“四層”“四翼”的角度對高考真題予以分類整理,歸納總結出一類試題的通性通法, 使得學生跳出“題海”, 高效備考.2023 年高考一共有九套試卷(全國甲、乙卷的文、理卷,新高考的I、Ⅱ卷,北京卷、上海卷和天津卷),筆者梳理解三角形問題,發現共有7 道試題以“爪形”三角形為背景考查解三角形知識,而通過深入分析這7 道試題,基于“四翼”的角度可以將其歸納為三類,基礎性試題、綜合性試題、創新性試題,文中分別選取典型試題予以分析,以幫助讀者掌握三類試題的解法,提高數學核心素養和解題能力.

