“數(shù)形結(jié)合”思想在判定函數(shù)零點個數(shù)上的應(yīng)用

尤長盤

【摘 ?要】 “數(shù)形結(jié)合”思想是高中數(shù)學(xué)中一個重要的解題思想，在求解代數(shù)問題時，借助圖形的生動性和直觀性，來表明數(shù)之間的聯(lián)系.一方面可以簡化解題的過程，另一方面對問題有更全面直觀的把握.根據(jù)函數(shù)圖象的交點判定函數(shù)零點個數(shù)是“數(shù)形結(jié)合”思想的一個重要運用，在計算零點個數(shù)時，結(jié)合圖象可以使得思維更嚴(yán)密，分析更充分，避免錯算、漏算.本文列舉兩道運用“數(shù)形結(jié)合”思想來判定函數(shù)零點個數(shù)的例題，詳述這種問題的解題思路，并對解題核心點做出歸納總結(jié)，破解其思維過程.希望可以幫助學(xué)生在遇到判定函數(shù)零點個數(shù)問題時提高解題效率和正確率.

【關(guān)鍵詞】 ?高中數(shù)學(xué)；數(shù)形結(jié)合；函數(shù)零點

在歷年的高考數(shù)學(xué)中，對函數(shù)零點個數(shù)的考查幾乎是一個必考問題，每年都會出現(xiàn)在一些省份的考卷之中.這一知識點主要考查了學(xué)生對函數(shù)基本概念的應(yīng)用，以及數(shù)形結(jié)合思想的運用，要求學(xué)生對函數(shù)零點個數(shù)的判斷方法有較深的掌握.

例題已知函數(shù)，根據(jù)的不同取值，請判斷的零點個數(shù)：

（1）若，請問有幾個零點？

（2）若，請問有幾個零點？

（3）若，請問有幾個零點？

分析這是一道典型的運用圖象法求零點個數(shù)的問題，的圖象難以直接畫出，令，利用拆分的兩個函數(shù)圖象交點的個數(shù)來判斷零點個數(shù).因此這道題的解答需要先將函數(shù)拆成兩個函數(shù)和的差，而且恰好這兩個函數(shù)的圖象容易畫出，根據(jù)（即），從而通過函數(shù)和函數(shù)的圖象交點個數(shù)，來判斷函數(shù)的零點個數(shù).

解 ?令函數(shù)，

可得，

設(shè)，

根據(jù)圖象法判斷函數(shù)零點個數(shù)知：函數(shù)得零點個數(shù)即為函數(shù)和圖象的交點個數(shù).

（1）當(dāng)時，則有

畫出函數(shù)和的圖象，如圖1所示

函數(shù)與函數(shù)的圖象有兩個交點，即當(dāng)時，函數(shù)有兩個零點

（2）當(dāng)時，函數(shù)與函數(shù)的圖象存在相切的情況，因此可分為3種情況.

設(shè)時，函數(shù)的圖象與的圖象相切

①當(dāng)時，如圖2所示，與的圖象，有三個交點，即函數(shù)有三個零點

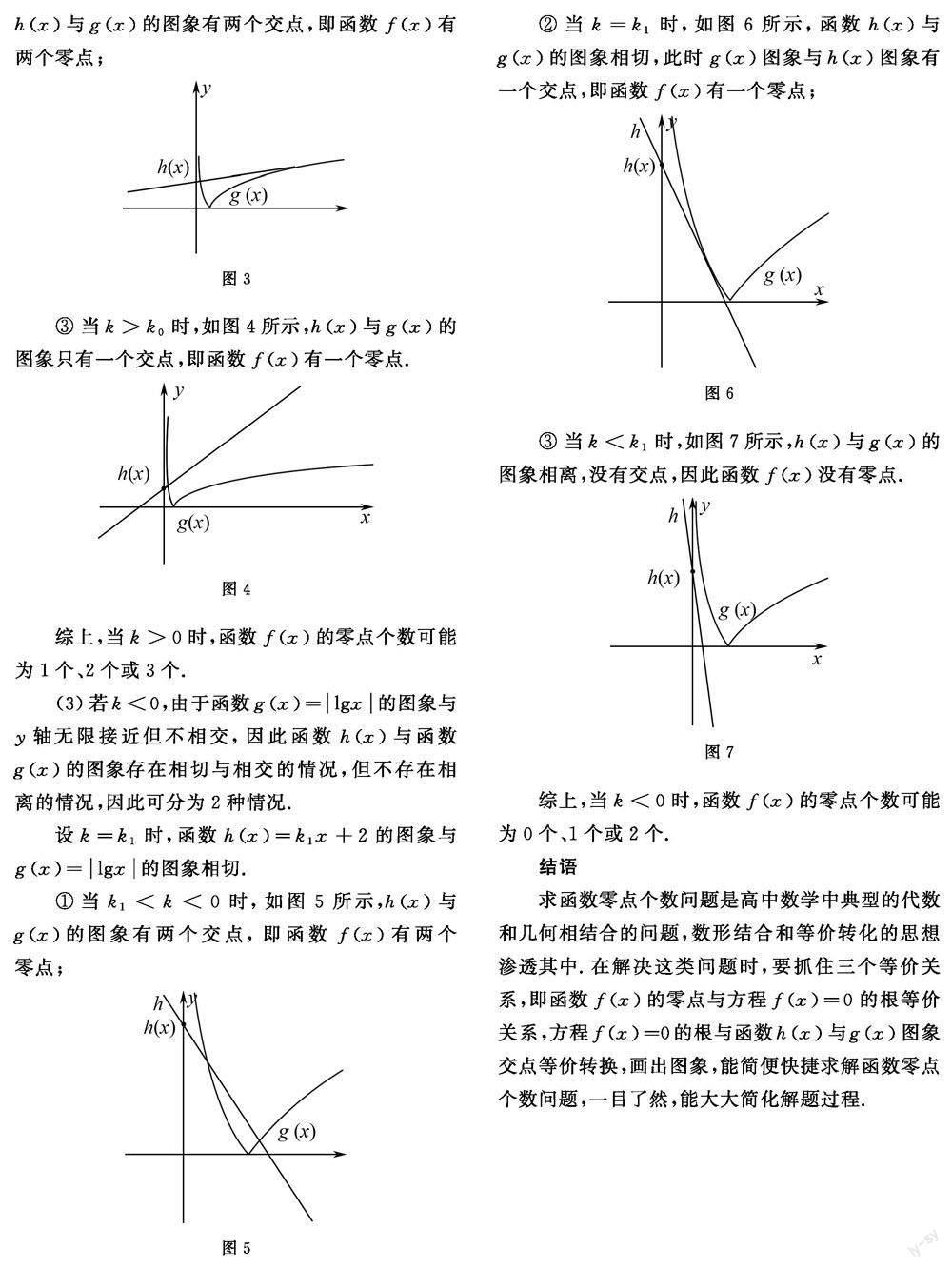
②當(dāng)時，如圖3所示，函數(shù)的圖象與的圖象相切，此時與的圖象有兩個交點，即函數(shù)有兩個零點.

③當(dāng)時，如圖4所示，與的圖象只有一個交點，即函數(shù)有一個零點.

綜上，當(dāng)時，函數(shù)的零點個數(shù)可能為1個、2個，或3個.

（3）若，由于函數(shù)的圖象與軸無限接近但不相交，因此函數(shù)與函數(shù)的圖象存在相切與相交的情況，但不存在相離的情況，因此可分為2種情況.

設(shè)時，函數(shù)的圖象與的圖象相切.

①當(dāng)時，如圖5所示，與的圖象有兩個交點，即函數(shù)有兩個零點.

②當(dāng)，如圖6所示，函數(shù)與的圖象相切，此時圖象與圖象有一個交點，即函數(shù)有一個零點.

③當(dāng)時，如圖7所示，與的圖象相離，沒有個交點，因此函數(shù)沒有零點.

綜上，當(dāng)時，函數(shù)的零點個數(shù)可能為0個、1個、或2個.

結(jié)語

求函數(shù)零點個數(shù)問題是高中數(shù)學(xué)中典型的代數(shù)和幾何相結(jié)合的問題，數(shù)形結(jié)合和等價轉(zhuǎn)化的思想滲透其中.在解決這類問題時，要抓住三個等價關(guān)系，即：函數(shù)的零點與方程的根等價關(guān)系，方程的根與函數(shù)與圖象交點等價轉(zhuǎn)換，畫出圖象，簡便快捷的求解函數(shù)零點個數(shù)問題，一目了然而且大大簡化解題過程.