新高考試題研討

王燕

【摘 ?要】本文對近兩年新高考試題各專題的分值進行對比、總結試題特點，并通過原題重現生動具體地給予論證，特別分析實際應用部分的試題，并附詳細解析過程.進而根據學科特點聯系實際教學，給出具體的教學建議.

【關鍵詞】 新高考；學科素養；高中數學

作為最后一批實行新高考的省份之一，身邊的教師們早已關注新高考試題已久，現將我自己在完成2021、2022兩年的新高考四套試題的過程中的一些感受和體會進行分享，不足之處敬請指正.

1 ?試題分析

1.1 ?專題對比

1.2 ?特點分析

專題分布均勻，梯度合理，聚焦核心素養，考查關鍵能力，命題更加靈活，對學生聯系實際、臨場應變能力提出更高要求.

特點1 ?聚焦核心素養，考查關鍵能力

新高考數學試題繼續貫徹德智體美勞全面發展的教育方針，突出數學學科的本質，堅持學科素養的導向、能力為重的原則，設計真實情境，倡導學以致用，體現應用價值。

實際應用一直是高考數學的熱點之一，在繼金字塔、維納斯、鋼琴鍵盤等美好的數學問題之后，越來越多的數學試題逐漸更接地氣、貼近生活，展現了數學學科較強的實用性.

例1 ?（2021年Ⅰ卷16）某校學生在研究民間剪紙藝術時，發現剪紙時經常會沿紙的某條對稱軸把紙對折.規格為的長方形紙，對折1次共可以得到，兩種規格的圖形，它們的面積之和，對折2次共可以得到，，三種規格的圖形，它們的面積之和，以此類推.則對折4次共可以得到不同規格圖形的種數為__________；如果對折n次，那么____.

本題以中國民間剪紙藝術為背景，考查數列相關知識與歸納推理相結合，綜合性強，層次較豐富.

解析（列舉+歸納）將題目中的數據整理推斷可知，對折n次后，可以得到（n+1）種不同規格的圖形，故對折4次后，可以得到5種不同規格的圖形.

對折n次后各規格圖形面積之和為

故

記，

所以①

②

①-②可得

②-所以

所以.

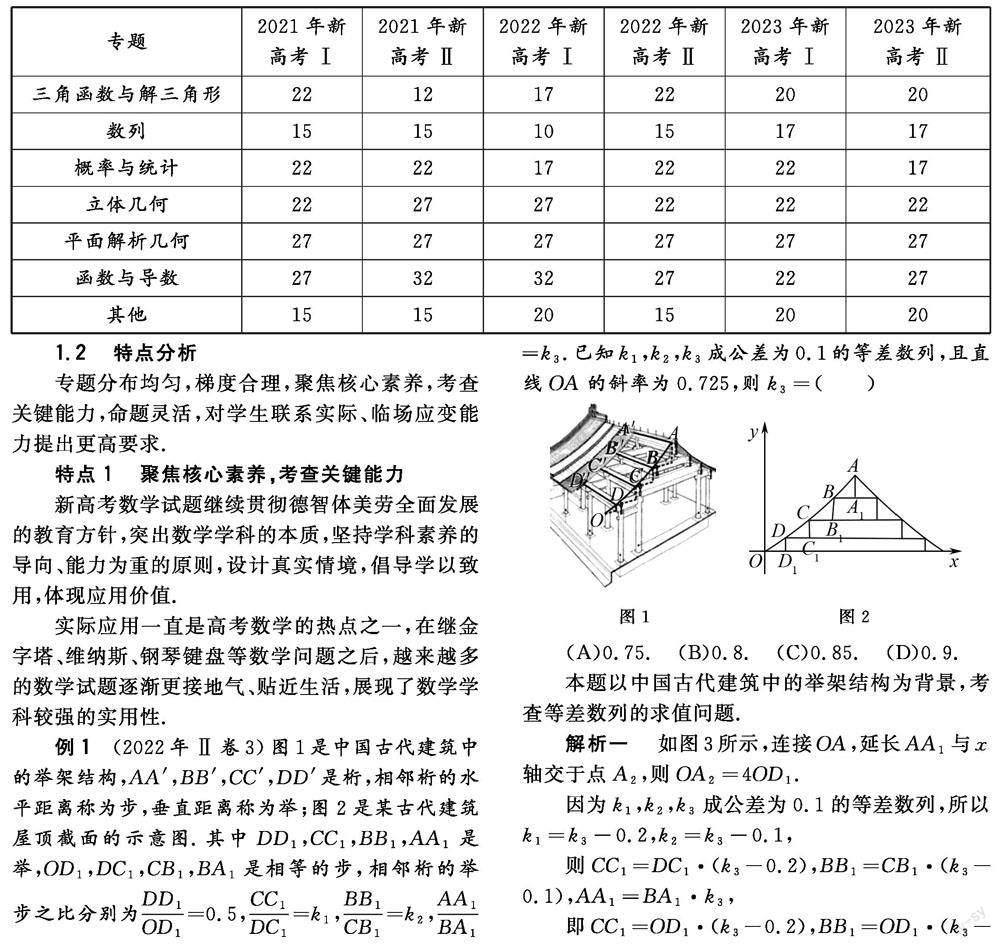
例2 ?（2022年Ⅱ卷3）圖1是中國古代建筑中的舉架結構，是桁，相鄰桁的水平距離稱為步，垂直距離稱為舉，圖2是某古代建筑屋頂截面的示意圖.其中是舉，是相等的步，相鄰桁的舉步之比分別為.已知成公差為0.1的等差數列，且直線OA的斜率為0.725，則（ ??）

（A）0.75.????????（B）0.8.??????（C）0.85.????????（D）0.9.

本題以中國古代建筑中的舉架結構為背景，考查等差數列的求值問題.

解析一如圖3，連接OA，延長與x軸交于點，則.

因為成公差為0.1的等差數列，所以，

則，

即.

又，所以，

且，

由于，

所以. ??故選（D）.

解析二 ?設，

則.

因為成公差為0.1的等差數列，

所以，

且，

即，所以. ???故選（D）.

除此之外，“一帶一路”、“衛星導航系統”、“微生物群體繁殖”、“南水北調”、“地方性疾病與當地居民的衛生習慣”等問題都出現在試卷中，應用之廣泛，形式之多樣已是前所未有，“兩耳不聞窗外事，一心只讀圣賢書”的學習者終將被淘汰.

特點2 ?凸顯學科特點，彰顯教育功能

高中數學學科素養包括數學運算、邏輯推理、直觀想象、數學建模、數據分析和數學抽象等，這也學科的特點，重視能力考查一直都是重中之重，如此，尚能彰顯教育功能.

例3??（2021年Ⅰ卷7）若過點可以作曲線的兩條切線，則（ ??）（A）. ?????（B）. ?????（C）. ??????（D）.

題干簡單清晰，落腳比較大小，主要考查指數函數和導數的幾何意義.

解析一??設切點為，切線方程為，

因為過點，則，

由兩條切線可知方程有兩個根.

令則，

則函數在上遞增，在上遞減.

由可得.故選（D）.

解析二 ?因為過點可作兩條切線，

所以點只能在圖象的下方，即.

由，可知兩條切線斜率均為正，故選（D）.

一是代數方法進行求解判斷，二是數形結合進行直觀推斷，還可以兩種方法雙管齊下、相輔相成，體現了靈活性和開放性.

例4??（2022年Ⅱ卷14）曲線過坐標原點的兩條切線的方程為?????.

題干直接明了，由于絕對值的出現，去絕對值是當務之急，去掉之后自然就是分類進行求導，題目也是主要考查了考生的應變能力和分析能力.

解析 ?當時，，

設切點為，則切線方程為.

因為過原點，所以，即，

所以切線方程為即.

當時，，

設切點為，則切線方程為.

因為過原點，所以，即，

所以切線方程為 ????即.

綜上兩條切線的方程分別為，.

另外，適當地利用函數的奇偶性，也可以減少重復運算.

2 ?教學建議

2.1 ?重視教材，把握基礎，提升能力

教材用最簡潔的敘述，從引入、創設問題到抽象概括逐層地展現知識，正是發現問題、解決問題、歸納總結的過程.除此之外例題、習題也能使原本抽象的概念、知識點更加具體化，幫助學生對鞏固，可以從題型、解法或數學思想等方面對學生進行引導.

2.2 ?關注知識能力的后期發展

后期發展主要是在掌握基礎的前提下，提升應用意識、能力培養和思維拓展，加強應用意識也是教育改革的需要，能力培養主要方向也是高中數學學科素養，同時也要重視數學思想方法.思維拓展初期是仿學，其次是觸類旁通、一題多解，最高層次便是舉一反三、一題多變.