基于灰狼算法的輪轂電機汽車懸架性能優化

段慧清 王鵬 葛祥旭

（北京理工大學前沿技術研究院，濟南 250300）

1 前言

輪轂電機具有平臺適應性強、驅動靈活、節省車內空間等優點，但不可避免地帶來非簧載質量增加的問題，通用汽車平臺在集成輪轂電機后，勢必需要進行懸架優化與調校，以保證整車的舒適性與操控性。

針對此問題，專家學者進行了深入研究，提出了不同方法。文獻[1]運用均勻設計法設計了變量的組合方案，獲得了約束條件與優化變量的顯式關系，應用遺傳算法獲取了最優參數。文獻[2]運用灰狼算法對可控阻尼的半主動懸架的關鍵參數進行了設計。文獻[3]提出了主動懸架的PID 控制策略。文獻[4]應用切換系統理論對半主動空氣懸架的控制模式和模式切換過程進行了研究。文獻[5]從電動汽車能耗角度，提出了一種被動懸架參數優化方案。

目前，實際車型仍以配備被動懸架為主，針對以上問題，本文結合多方研究成果，以前后懸架的剛度、阻尼為優化變量，以懸架綜合性能最優為優化目標，運用灰狼優化算法求解最優目標下的變量組合。

2 系統模型的建立

2.1 半車被動懸架模型

前、后半車懸架模型可以很好地反映車身的垂直振動與俯仰運動，故本文選擇半車模型為研究對象，建立半車被動懸架的動力學模型如圖1 所示。其中ks1、ks2分別為前、后懸架的彈簧剛度，cs1、cs2分別為前、后懸架的阻尼，I為半車的轉動慣量，φ為車身俯仰角度，zc為質心位移，mc為半車質量，mt1、mt2分別為前、后軸非簧載質量，zs1、zs2分別為前、后軸簧載質量位移，zt1、zt2分別為前、后輪胎位移，zr1、zr2分別為前、后軸路面激勵，kt1、kt2分別為前、后輪胎的剛度，a、b分別為質心到前、后軸的水平距離。

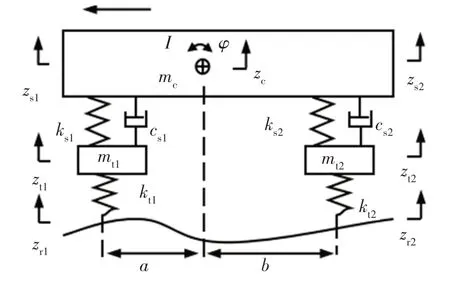
圖1 半車被動懸架的動力學模型

根據牛頓運動定律，可以列出模型的相關微分方程組，其質心運動方程可表示為：

車身俯仰運動的微分方程為：

前、后非簧載質量的運動微分方程分別為：

在φ很小的情況下，前后簧載質量位移、半車質心位移、俯仰角之間的關系為：

對于路面輸入，采用濾波白噪聲模擬路面激勵zr(t)的時域模型為[6]：

式中，n1=0.011 m-1為路面不平度下的截止空間頻率；n0=0.1 m-1為參考空間頻率；v=25 m/s 為車速；Gq(n0)為路面不平度系數，本文采用C 級路面，取Gq(n0)=2.56×10-4m3；w(t)為白噪聲。

前、后車輪的路面激勵相同，但存在一定的時間差。在模型中，可通過為前輪路面激勵增加時間延遲模塊來建立后輪路面激勵模型。

2.2 模型建立

根據以上微分方程與路面激勵模型，在MATLAB/Simulink 中建立半車懸架振動模型，選取質心加速度、車身俯仰角加速度、前后懸架動撓度、前后懸架動載荷為輸出量，如圖2 所示，其中cs1、cs2、ks1、ks2為可優化的變量。

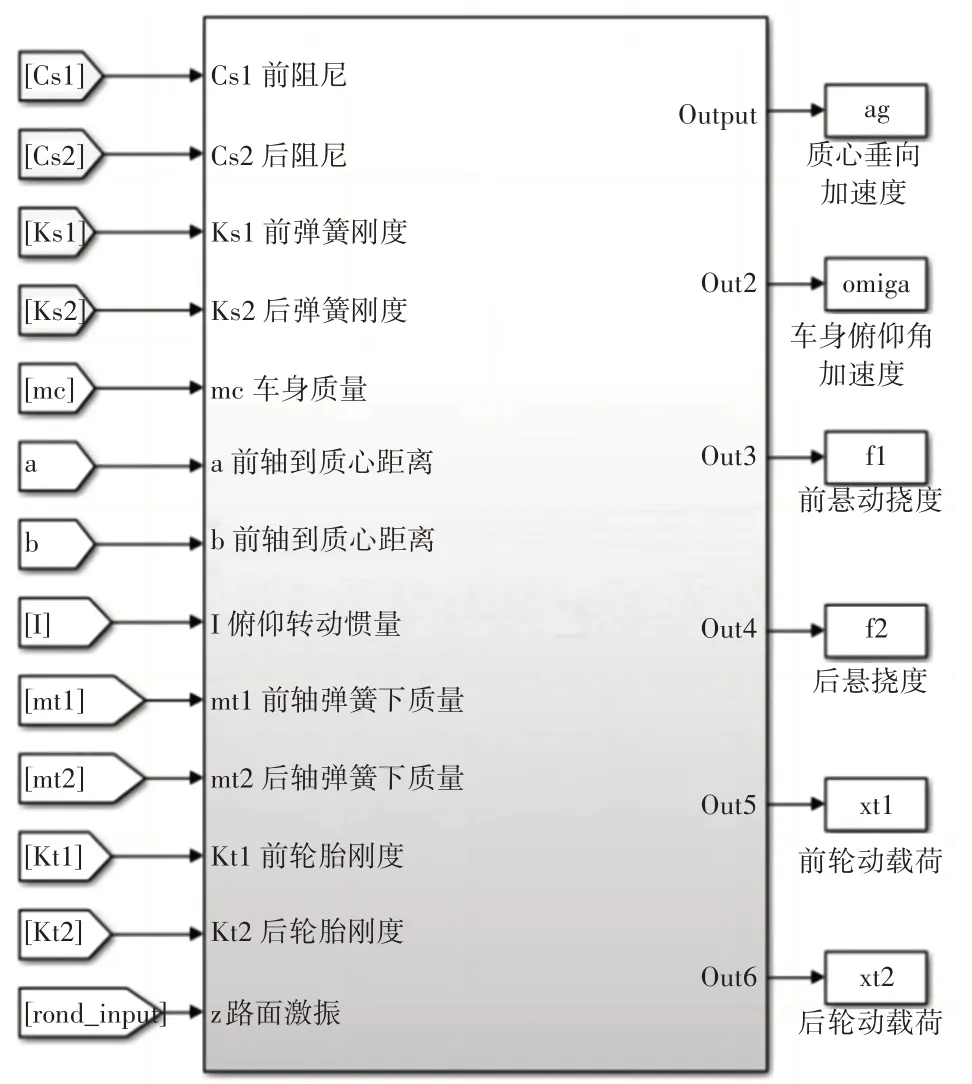
圖2 半車懸架振動模型

3 仿真優化設置

集成輪轂電機后，選取ks1、ks2、cs1、cs2作為優化變量，在設定的范圍內，用優化算法尋找最優的變量值。

為保證懸架上、下運動時不撞擊限位塊，以免引起懸架性能惡化，令懸架動撓度均方根值δf小于撓度上限[δfd]的1/3，可保證懸架撞擊限位塊的概率小于0.3%。已知原車動撓度最大值為0.06 m，車輪動載荷均方根值小于G/3，可保證車輪跳離地面的概率小于0.15%[7]。綜上，優化的約束條件為：

式中，δf1、δf2分別為前、后懸架動撓度均方根；δd1、δd2分別為前、后輪動載荷均方根；G1、G2分別為前、后軸載荷。

懸架的性能指標中，質心加速度、俯仰角加速度可反映車身的振動水平，影響乘坐舒適度。根據ISO 2631-1《人體承受全身振動評價：一般要求》[8]，質心加速度和俯仰角加速度的加權系數分別為1和0.4，故可列出行駛舒適度評價指標Q1的計算公式：

式中，δa0、δa分別為集成輪轂電機前、后質心加速度均方根；δb0、δb分別為集成輪轂電機前、后俯仰角加速度均方根值。

懸架動撓度在一定程度上可以同時反映車輛的乘坐舒適性和操縱穩定性[9]，并與車輛的許用動行程有關。車輛懸架動撓度的評價指標Q2計算公式為：

式中，δf10、δf1分別為集成輪轂電機前、后前輪動撓度均方根；δf20、δf2分別為集成輪轂電機前、后后輪動撓度均方根。

車輪動載荷能夠反映車輛操縱穩定性，其評價指標Q3計算公式為：

式中，δd10、δd1分別為集成輪轂電機前、后前輪動載荷均方根；δd20、δd2分別為集成輪轂電機前、后后輪動載荷均方根。

綜合以上評價指標，以3 個指標的加權平均值最小為優化目標，集成輪轂電機后半車懸架的優化代價函數F整理為：

式中，w1=2、w2=2、w3=1分別為Q1、Q2、Q3的權值。

4 灰狼算法

灰狼優化算法是一種群體智能算法[10]，具有實現簡單、控制參數少、全局搜索能力強、求解精度與收斂速度均衡等優點。

灰狼算法模擬了灰狼群體的社會等級與捕獵機制。狼群等級被簡化為2 個層級：α、β、δ為3 匹頭狼，設定從α到δ，頭狼的地位依次降低；ω為低層級狼，數量若干，聽命于頭狼，圍繞3 匹頭狼的位置進行捕獵。灰狼算法迭代過程的數學模型可概括為頭狼占位、ω狼隨機包圍和加權更新。

a.頭狼占位。在算法應用中，每只灰狼的位置代表解空間中的一個可行解，算法初始時隨機生成一組解，組成初始灰狼群，然后經計算將本輪的最優位置依次賦值給3 匹頭狼α、β和δ，則α代表當前找到的最優解，β和δ分別代表次優解。

b.ω狼隨機包圍。ω狼圍繞著3 匹頭狼生成新一輪的位置，從而實現3 匹頭狼指引群體朝著搜索空間的最優方向移動。

散捕獵過程中，灰狼與獵物（本輪3匹頭狼暫居的位置）的距離為：

式中，D為灰狼群個體與獵物的距離向量；C為0～2范圍內的隨機數；Xp(i)為獵物，即頭狼在第i輪迭代中的位置向量；X(i)為灰狼在第i輪迭代中的位置向量。

狼群個體在下輪迭代中圍繞獵物的位置為：

式中，A=2a·r-a為系數向量，當|A|＞1時，狼群遠離獵物去搜索其他目標，當|A|＜1時，狼群靠近攻擊獵物；r為0～1范圍內的隨機向量；a為初始值為2的常數，隨著迭代次數的增加，從2線性減小到0。

由式（12）可知，D為一個帶有隨機因數的距離向量，式（13）使狼群個體圍繞上一輪頭狼位置隨機分布。但狼群中有3匹頭狼，根據式（13），每匹頭狼都能生成狼群個體下輪迭代的位置，這就需要進一步完成最終的位置更新。

c.加權更新。圍繞3 匹頭狼依次生成狼群的位置向量X1、X2、X3分別為：

式中，Xα、Xβ、Xδ分別為3匹頭狼的位置；C1、C2、C3為3匹頭狼對應的隨機數；A1、A2、A3為3匹頭狼對應的系數向量；Dα、Dβ、Dδ分別為3匹頭狼與個體間的距離。

設定3 匹頭狼對狼群的影響權重相同，則狼群根據α狼、β狼和δ狼的位置更新下一輪的位置[11]：

灰狼算法會多次迭代重復以上過程，從而搜尋更優解[11]。

5 系統優化與分析

使用m 語言編輯灰狼優化算法，以代價函數最小為目標，在約束條件范圍內，調用Simulink 模型（見圖2）進行聯合優化仿真。輪轂電機汽車模型的初始參數如表1 所示，其中ks1、ks2、cs1、cs2為待優化的變量，變量的范圍為各自初值的75%～125%。mt1、mt2中已包含輪轂電機的質量，其數值相較于未安裝輪轂電機時增大了30 kg。

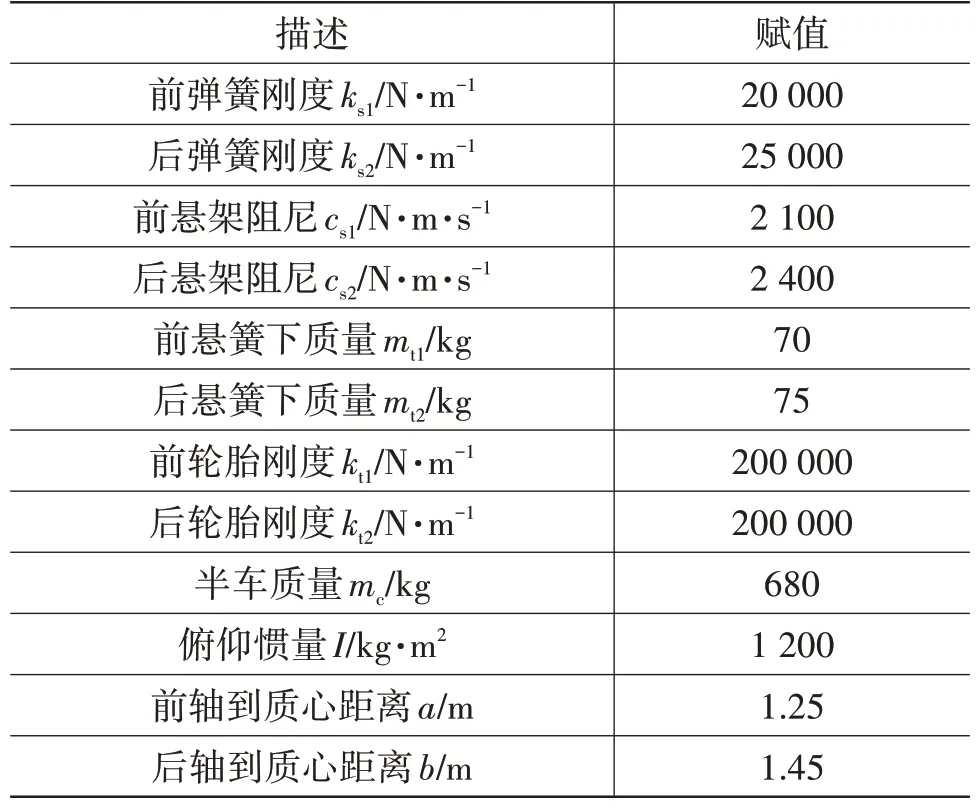
表1 輪轂電機汽車模型初始賦值

為驗證灰狼算法的優化能力，選擇粒子群算法作為對比算法。運用2種優化算法與半車懸架模型進行聯合仿真，2 種算法的種群個體數量均設置為25 個，迭代次數均設置為20 次，運行2 種算法后可得到代價函數最優情況下變量的解。2 種算法的迭代曲線如圖3 所示，從圖3 中可以看出，粒子群算法陷入了局部最優，過早收斂使其未找到全局最優解，相較于粒子群算法，灰狼算法尋找到更優的解，使代價函數的值更小。

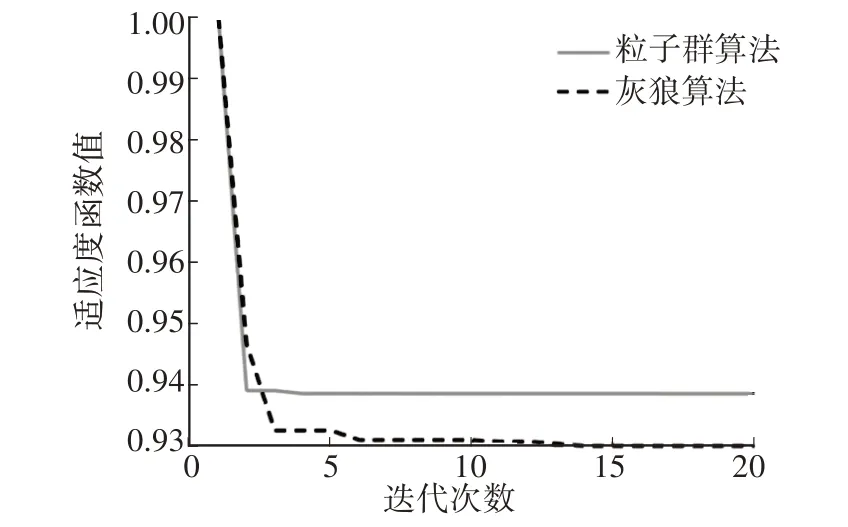
圖3 灰狼算法與粒子群算法對比

灰狼算法尋找的最優解經過圓整后如表2 所示。

表2 優化后變量值

經過優化的輪轂電機汽車懸架質心加速度、俯仰角加速度、前后懸架動撓度、前后輪動載荷與原型車時域響應對比如圖4所示。

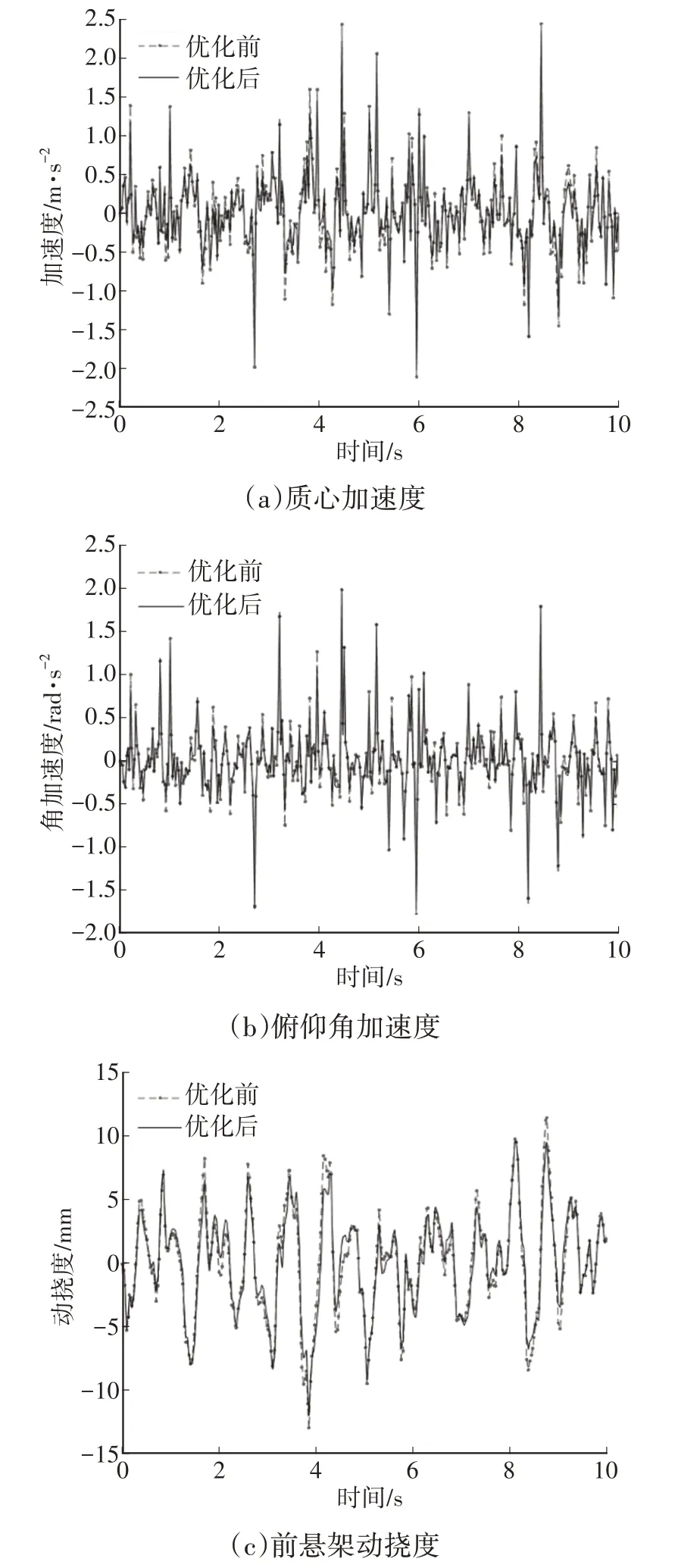
圖4 優化前、后各變量時域響應結果對比

分析系統仿真結果，列舉優化前、后質心加速度、俯仰角加速度、前后懸架動撓度、前后輪動載荷的均方根值，如表3所示。

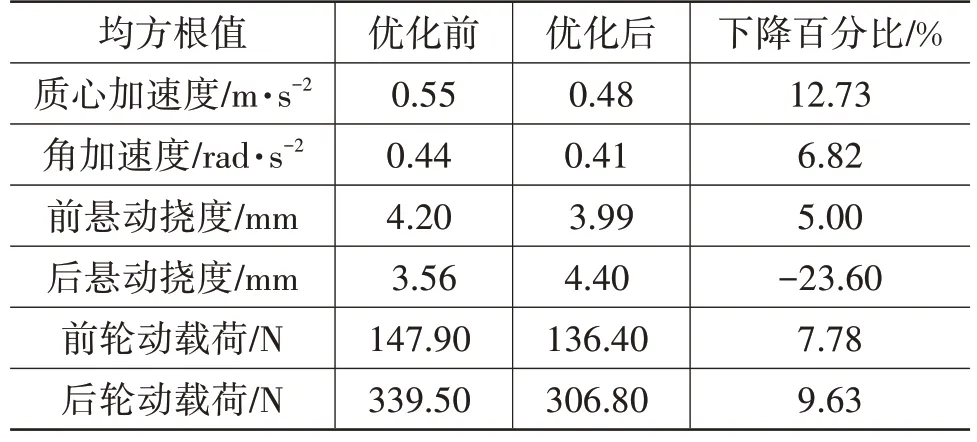
表3 優化前、后均方根對比

從表3 中可以看出，經優化的輪轂電機半車懸架與原型車相比：質心加速度均方根值、角加速度均方根值均明顯下降，表明整車的乘坐舒適性得到有效提升；前懸架動撓度均方根值明顯下降，后懸架動撓度均方根值大幅提高，但優化后均方根值為4.4 mm，仍遠小于最大動撓度的1/3，即仍在約束條件20 mm 以內；前、后輪動載荷下降，性能均有所提升。表3 中數據表明，經過優化設計，與原車相比，集成輪轂電機的汽車懸架整體性能得到有效提升。

6 結束語

本文在半車懸架模型基礎上，根據懸架的評價指標，設計了以原型車懸架性能為參考的優化代價函數，然后利用灰狼優化算法，以代價函數最小為目標，搜尋最優的懸架的剛度、阻尼參數。

仿真數據表明，相較于粒子群算法，灰狼算法更能避免局部最優，并能在復雜的模型中搜索到使代價函數最優的變量組合。在設定的約束條件范圍內，懸架性能的評價指標質心加速度、俯仰角加速度、輪胎動載荷均有所降低，其中質心加速度的優化效果最顯著，表明電動汽車在集成輪轂電機使非簧載質量增加后，通過科學設置約束條件與優化目標，使用灰狼算法進行性能優化，可使懸架綜合性能，尤其是舒適性能得到有效提升。