應(yīng)用于線上會議系統(tǒng)的改進仿射投影符號算法

魏丹丹， 吳軍， 周翊

1. 遵義師范學院 信息工程學院，貴州 遵義 563002；2. 重慶郵電大學 通信與信息工程學院，重慶 400065

得益于5G通信技術(shù)成熟和業(yè)務(wù)的蓬勃開展, 寬帶語音給用戶帶來了更優(yōu)質(zhì)的接近面對面交流的溝通體驗． 目前, 用戶在各類線上會議軟件的注冊量或者使用以每年數(shù)10倍甚至更多倍數(shù)的速度增長． 但是, 目前線上會議系統(tǒng)的研究還存在許多亟待解決的現(xiàn)實應(yīng)用問題, 例如現(xiàn)有會議系統(tǒng)中搭載的自適應(yīng)濾波器回聲消除算法(Acoustic Echo Cancellation, AEC)在脈沖噪聲干擾或雙端對講情況下經(jīng)常存在發(fā)散的問題[1], 實時性要求得不到保證[2]． 因此, 創(chuàng)建能夠克服這一問題并提升用戶體驗的回聲消除算法是當前的主要任務(wù)． 回聲消除算法在線上會議系統(tǒng)的應(yīng)用主要是遠端用戶將語音信號從發(fā)送室傳到近端接收室, 遠端語音信號通過揚聲器播放出來, 經(jīng)過房間的回波路徑不停反射后得到回聲信號, 該信號同背景噪聲一起被話筒拾取得到期望信號． 而回聲消除算法不斷迭代更新權(quán)重系數(shù)實現(xiàn)對回聲路徑建模, 從而估計出回聲信號[3-4]． 基于最小均方誤差準則(Minimum Mean Square Error, MMSE)的歸一化最小均方(Normalized Least Mean Square, NLMS)算法[5]、 迭代最小均方(Recursive Least Mean, RLS )算法[6]及各類變形算法由于計算復(fù)雜度低, 結(jié)構(gòu)簡單等優(yōu)點被廣泛應(yīng)用到回聲消除中, 但是卻無法克服輸入語音信號高度相關(guān)的影響[7]． 對此, Wang等[8]提出一種通過多個輸入向量更新權(quán)重系數(shù)的仿射投影(Affine Projection Algorithm, APA)算法, 但是APA收斂速度加快是以計算復(fù)雜度增加為代價的． 此外, 在非高斯干擾下, APA算法性能因為“2-范數(shù)準則”特征有所下降, 并利用低階規(guī)范對非高斯噪聲的魯棒性[9-10]提出了基于經(jīng)典“1-范數(shù)準則”的一種無矩陣求逆的仿射投影符號算法(Affine Projection Sign Algorithm, APSA)[11]． 但是步長因子和正則因子控制的跟蹤性能無法滿足工程實踐的需求, 為了同時滿足收斂速度快和穩(wěn)態(tài)誤差小的跟蹤性能要求[12], 一種基于凸組合方式的算法[13]被提出, 所謂凸組合[14]就是一種利用兩個步長參數(shù)進行換擋操作的技術(shù)． 小步長參數(shù)和大步長參數(shù)分別控制誤差矢量和收斂速度． 凸組合技術(shù)最早是應(yīng)用在LMS算法中, 文獻[15]首次將凸組合技術(shù)引入APA算法中, 接著一系列改進凸組合仿射投影算法甚至凸組合3個獨立濾波器抽頭系數(shù)的方案被提出[16-17], 從而提高了算法總體性能．

有學者在對線上會議系統(tǒng)中的雙端講話干擾和脈沖噪聲問題深入研究的基礎(chǔ)上, 提出了一種改進型凸組合仿射投影符號算法． 該算法首先在AEC中加入雙端檢測(Double Talk Detection, DTD)[18], DTD方案一般有兩種形式: 一種是比較遠端語音信號和近端麥克風信號的能量, 如著名的廣泛應(yīng)用于線路回波消除(Line Echo Cancellation)中的Geigel法[19]; 另一種是通過檢測遠端和近端麥克風信號之間的相關(guān)性來判斷DT(Double Talk)． 原理在于回波信號與遠端語音信號高度相關(guān), 而近端語音與遠端語音的相關(guān)性卻很低． 相關(guān)檢測可通過計算遠端信號與近端信號的互相關(guān)矢量來實現(xiàn)． 然后, 對噪聲建模, 用新的非線性函數(shù)替代原算法中的Sign函數(shù)對噪聲性能進行提升, 防止算法在脈沖噪聲影響下發(fā)散．

1 APA及改進算法

本文基于圖1所示線上會議系統(tǒng)的聲學回聲消除系統(tǒng)框圖進行分析[20], 輸入語音信號x(n)經(jīng)過回波路徑濾波器為h(n)的發(fā)射室產(chǎn)生回波y(n), 該回波信號與加性噪聲v(n)一起被麥克風拾取構(gòu)成期望信號d(n)． 聲學回波路徑由一個自適應(yīng)有限脈沖響應(yīng)(Finite Impulse Response, FIR)濾波器w(n)建模, 濾波器輸出信號和麥克風輸入端信號相比較, 得到誤差信號, 通過最小均方誤差代價函數(shù)對自適應(yīng)濾波器的抽頭系數(shù)進行調(diào)整, 最終使包含期望信號的目標函數(shù)得到最小化值． 自適應(yīng)濾波器w(n)與聲學回波路徑h(n)的長度L相同．

圖1 線上會議系統(tǒng)的AEC設(shè)置

1.1 仿射投影算法APA

APA是一種數(shù)據(jù)重用算法, 它不僅利用當前的輸入矢量進行濾波器系數(shù)更新, 而且重復(fù)利用過去的K-1個輸入矢量,K為算法投影階數(shù)． 假定輸入噪聲v服從均值為零, 方差為σ2的高斯分布, APA的更新公式可由一個受線性約束的最小化表達式推導(dǎo), 即

(1)

(2)

1.2 仿射投影符號算法APSA

線上會議系統(tǒng)中的輸入語音信號具有高度相關(guān)性, 傳統(tǒng)算法收斂速度明顯降低, 而APA算法具有降低相關(guān)的特性, 輸入語音信號嚴重相關(guān)時仍能快速收斂而不引起算法失調(diào)． 但是, 算法在外界噪聲影響下的魯棒性能較差, 算法性能嚴重衰退． 為了克服對自適應(yīng)濾波算法的不利影響, 文獻[11]提出了仿射投影符號算法, 基于l1范數(shù)的符號函數(shù)APSA算法在某種程度上可以視為APA與符號算法的結(jié)合, 算法描述如下所示:

(3)

(4)

ei,p≈ei

(5)

ei=di-yi

(6)

(7)

式(3)-式(7)中, ‖·‖1是矢量的l1范數(shù),γ是將約束條件改為無約束代價函數(shù)時引入的拉格朗日乘子, sign(·)是符號函數(shù)． 由于后驗誤差矢量ei,p在實踐中無法獲得, 將其替代為近似的先驗誤差矢量ei．

1.3 凸組合仿射投影符號算法CC-APSA

凸組合技術(shù)是一種組合因子的迭代方法, 為工程實踐提供了很好的解決方案． 與APSA固定步長方案不同的是, CC-APSA算法應(yīng)用凸組合技術(shù)獨立運行兩個不同步長來同時滿足自適應(yīng)濾波算法對高收斂速度和低穩(wěn)態(tài)誤差的需求． 其中一個用大步長μ1來保障算法的快速收斂, 另一個用小步長μ2來保障算法的低穩(wěn)態(tài)誤差． 最終CC-APSA算法性能優(yōu)于其中任何一個步長的自適應(yīng)濾波算法． 算法的整體輸出表示為

yi=λiy1,i+(1-λi)y2,i

(8)

λi=sgm[αi]=1/(1+e-αi)

(9)

式(9)中,αi的自適應(yīng)更新基于最小誤差l1范數(shù)采用梯度下降方案求出, 即

(10)

式(10)中,μα是αi的自適應(yīng)更新步長, 文獻[15]建議αi應(yīng)被限定在對稱區(qū)間[-α+,α+]內(nèi), 并指出將其設(shè)定為4是合適的選擇． 因此, 修改式(4)得到CC-APSA算法的更新公式為

(11)

式(11)中,β是光滑因子．

2 雙端講話干擾推導(dǎo)

線上會議系統(tǒng)中的雙端講話檢測(DTD)是一個難點, 基于信號包絡(luò)檢測的DTD是一種低運算量的算法, 該方法通過比較遠端語音信號和近端麥克風信號的能量進而作出相應(yīng)的DT判斷[22]． 這點和Geigel方法性質(zhì)類似． 但是, Geigel方法比較的是單個數(shù)據(jù)點的絕對值, 檢測函數(shù)的變化非常劇烈． 為了得到更準確穩(wěn)定的判據(jù), 信號保羅檢測法采用的是信號能量而非單個數(shù)據(jù)點． 通過IIR濾波平滑的方式來計算信號包絡(luò)作為信號能量的度量, 然后比較相關(guān)的估計值得出DT判斷． 其中, 輸入語音信號能量為:

vx(n)=αvx(n-1)+(1-α)|x(n)|

(12)

式(12)中,α=0.99是遺忘因子, 麥克風信號能量為:

vd(n)=αvd(n-1)+(1-α)|d(n)|

(13)

檢測函數(shù)因此可以計為

(14)

式(14)中, 參數(shù)γ在只有背景噪聲時用來限制檢測函數(shù)的取值, 一般設(shè)為0.05． 通常情況下, 回波能量相對于遠端語音信號能量較弱, 且近端語音信號能量比回波能量高． 因此, 檢測函數(shù)的值會隨著DT出現(xiàn)而顯著增大, 并隨著DT結(jié)束而減小． 將檢測函數(shù)值和一個閾值T相比較, 就可以做出相應(yīng)的判斷． 由于語音信號的能量具有時變特性, 固定閾值T方案不是好的選擇, 必須設(shè)計一個能跟蹤信號能量變化的時變閾值T(n)． 當自適應(yīng)濾波器收斂后, 其輸出y(n)可以近似地認為等同于真實的回波, 因此可以用來作為時變閾值的參考, 于是有:

(15)

式(15)中,κ=0.02是一個小的正數(shù), 用來為檢測誤差留下一點余地． 比較兩者的值可以給出DT判斷． 其中,vx(n)的作用可看作是為了增加算法準確度引入的一個歸一化處理．

3 一種新的凸組合仿射投影符號算法NCC-APSA

本節(jié)提出一種新的凸組合仿射投影符號算法NCC-APSA(Novel Covex Combination Affine Projection Sign Algorithm), 新算法用新的非線性Sigmoid函數(shù)類型替代原算法中的sign函數(shù), 在第2部分雙端講話干擾推導(dǎo)基礎(chǔ)上定義新的DT統(tǒng)計量g(n), 有效克服線上會議系統(tǒng)中的雙端對講干擾和脈沖噪聲干擾, 而且在收斂速度、 穩(wěn)態(tài)失調(diào)等方面依舊保持良好性能． 根據(jù)濾波器線性約束最小化表達式改寫為代價函數(shù)形式為:

(16)

利用負梯度最陡下降法, 對式(16)兩邊關(guān)于wi求導(dǎo):

(17)

令

-Usign(ei,p)+2γ(wi-wi-1)=0

代入約束條件和基于l1范數(shù)的凸組合技術(shù), 然后代入式(10)組合因子推導(dǎo)結(jié)果, 更新公式為:

(18)

為了保證算法在脈沖噪聲下的魯棒性, 將式(18)改進為更加平穩(wěn)的非線性函數(shù)sigmoid形式, 在算法實施時, 為了克服雙端對講干擾, 本文做了一點處理． 定義新的DT統(tǒng)計量g(n), 采用ζ(n)-T(n)作為檢測函數(shù), 通過試驗設(shè)計固定閾值和控制環(huán)節(jié)來實現(xiàn)更穩(wěn)定的DTD, 改進后的權(quán)重系數(shù)更新為:

(19)

式(19)中,g(n)由如下表達式獲得:

(20)

4 仿真結(jié)果和分析

本文基于MATLAB仿真平臺對算法性能進行模擬, 第1部分采用不同類型輸入信號和系統(tǒng)脈沖響應(yīng)分別分析APA算法、 APSA算法、 CC-APSA算法及NCC-APSA算法在收斂速度、 均方誤差和跟蹤能力等方面的性能． 第2部分則驗證改進型凸組合仿射投影符號算法在有雙端講話干擾的線上會議系統(tǒng)中的AEC性能．

4.1 算法性能對比

本節(jié)采用兩種不同類型的遠端輸入信號進行仿真, 8 kHz采樣頻率, 16 bit量化． 輸入信號如圖2是由零均值高斯隨機信號通過AR模型T(z)=1/(1-0.7z)產(chǎn)生, 信噪比SNR=30 dB． 圖3是仿真中系統(tǒng)辨識采用的兩種不同單位脈沖響應(yīng), 左邊是截斷長度為256階的汽車單位脈沖響應(yīng), 右邊是會議系統(tǒng)中常見的1 024階單位脈沖響應(yīng)． 兩種脈沖都不屬于典型的稀疏信道, 稀疏度分別為0.52和0.32． 衡量算法性能的指標為歸一化均方偏差(Normalized Mean Square Deviation, NMSD)[23], 用于度量自適應(yīng)濾波器與目標系統(tǒng)的逼近程度, 即回聲抑制能力, 其定義如下:

圖2 輸入高斯白噪聲信號

圖3 系統(tǒng)辨識

(21)

歸一化均方偏差包括穩(wěn)態(tài)誤差和收斂速度兩個跟蹤性能, 穩(wěn)態(tài)誤差越小, 代表回聲抑制效果越好, 而收斂速度代表算法需要多少次迭代才能達到理想的回聲抑制效果． 本文所有仿真曲線均是通過 50 次獨立實驗求平均值獲得．

4.1.1 穩(wěn)態(tài)輸入信號的算法性能對比

輸入圖2中自回歸模型下的高斯白噪聲, 期望信號由圖3的真實單位脈沖響應(yīng)產(chǎn)生, 無輸出噪聲．

作為第一步, 本文仿真了APA算法、 APSA算法、 CC-APSA算法和NCC-APSA算法在自回歸模型下的跟蹤性能, 圖4和圖5分別展示了L=256和L=1 024兩種系統(tǒng)辨識的情況． 實驗結(jié)果表明, 所提出的NCC-APSA算法具有優(yōu)秀的收斂速度和穩(wěn)態(tài)誤差, 當濾波器大小L=256時, CC-APSA算法和NCC-APSA算法無論是收斂速度還是穩(wěn)態(tài)誤差都好于APA算法、 APSA算法． CC-APSA算法和NCC-APSA算法收斂速度相似, 有幾乎相同的穩(wěn)態(tài)NMSD, 都是大約900次迭代后開始收斂． 當L=1 024時, 各算法性能均有不同程度的下降, 算法無法達到900次迭代的穩(wěn)態(tài), 但是可以看出CC-APSA算法跟蹤性能略微優(yōu)于NCC-APSA算法．

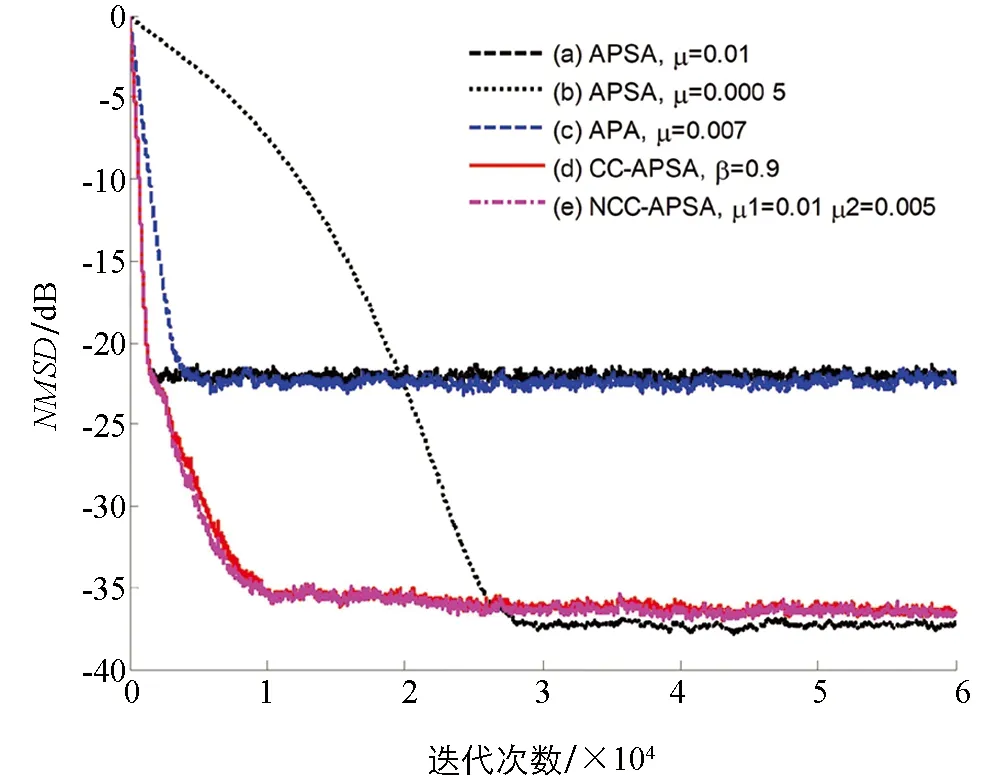
圖4 相關(guān)自適應(yīng)算法性能比較(汽車脈沖響應(yīng))

圖5 相關(guān)自適應(yīng)算法性能比較(會議系統(tǒng)脈沖響應(yīng))

4.1.2 脈沖噪聲模型下的算法性能對比

圖6 不同脈沖噪聲水平下算法跟蹤性能

圖7 相關(guān)自適應(yīng)算法待辨識系統(tǒng)突變的性能比較

4.1.3 語音輸入信號的算法性能對比

語音由于具有非平穩(wěn)特性和頻譜范圍大的特點而非理想的脈沖響應(yīng)激勵信號[25], 在實際應(yīng)用場景中, 輸入信號往往是語音信號而非高斯白噪聲, 所以本文采用真實語音信號進行仿真實驗, 材料取自一段中文男聲, 具有10～30 ms的準穩(wěn)態(tài)特性及高相關(guān)性． 本文對NCC-APSA算法使用語音信號作為輸入信號進行了對比實驗, 分別采取圖4所示的兩個單位回聲脈沖響應(yīng)進行濾波． 對于這兩個實驗, 本文都添加一個信噪比為50 dB的高斯白噪聲成分． 圖8和圖9分別顯示了長度為L=256的汽車系統(tǒng)和長度為L=1 024的線上會議系統(tǒng)的結(jié)果． 與APA、 APSA和CC-APSA算法相比, NCC-APSA算法在暫態(tài)和穩(wěn)態(tài)狀態(tài)下都具有良好的AEC性能．

圖8 語音輸入下相關(guān)自適應(yīng)算法跟蹤性能(汽車脈沖響應(yīng))

圖9 語音輸入下相關(guān)自適應(yīng)算法跟蹤性能(會議系統(tǒng)脈沖響應(yīng))

4.2 基于線上會議系統(tǒng)的算法驗證實驗

為了進一步驗證NCC-APSA算法的性能, 本文采用真實語音信號進行線上會議系統(tǒng)的回聲消除實驗, 分別在兩個不同房間進行音頻數(shù)據(jù)采集． 兩個房間分別配置了不同的普通家具家電, 發(fā)送室大小約為4.35 m×3.2 m×2.8 m(L×W×H), 接收室大小約為3.8 m×2.6 m×2.5 m(L×W×H)． 用于語料采集的器材包括電腦、 麥克風和揚聲器等, 揚聲器和麥克風分別擺放在電腦兩側(cè), 且兩者距離0.45 m左右． 電腦擺放在中間負責數(shù)據(jù)處理, 麥克風錄制遠端語音信號, 遠端信號經(jīng)過房間的回聲信道形成回聲后被麥克風拾取, 同時被拾取的還有近端信號和環(huán)境噪聲(圖10)．

圖10 單通道AEC軟、 硬件實驗設(shè)置

近端講話的語音內(nèi)容是一段中文男聲“園林采用新中式建造手法……”, 語音數(shù)據(jù)的采樣率設(shè)置為8 000 Hz, 根據(jù)房間實際脈沖來選擇截斷長度, 確定自適應(yīng)FIR濾波器階數(shù)L=1 024階． NCC-APSA算法處理結(jié)果如圖 11所示, 左邊是近端語音信號(長度設(shè)置為400 000)和雙端講話語音的時域波形圖, 語音信號在迭代次數(shù)為156 800時加入雙講語音, 其余設(shè)置為0, 無雙端對講影響． 圖11右側(cè)從上往下分別是麥克風信號和回聲消除后的輸出信號時域波形圖． 從圖11中可以看出, NCC-APSA算法可以有效地濾除回聲干擾噪聲, 聽感方面的回聲抑制效果也很好, 工程實踐中具有很高的實用價值．

圖11 信號時域波形圖

5 結(jié)論

針對線上會議系統(tǒng)中存在的雙端講話干擾和脈沖噪聲問題, 本文提出一種適用于線上會議系統(tǒng)的改進型仿射投影符號算法． 仿真結(jié)果表明, 該算法可以有效克服線上會議系統(tǒng)中的雙端對講干擾和脈沖噪聲干擾, 而且依舊保持良好的跟蹤性能． 盡管本文算法在一定程度上改善了算法性能, 但是沒有考慮稀疏信道下的性能優(yōu)化, 而且計算復(fù)雜度依然較高, 不利于實際應(yīng)用中推廣． 因此, 如何利用信道的稀疏先驗特性, 進一步開發(fā)適應(yīng)稀疏信道的低復(fù)雜度算法是下一步研究的重點工作．