經濟增長碳脫鉤的聯動效應研究
——基于“全國一盤棋”視角下的社會網絡分析

孫傳旺 陳智龍

(廈門大學,福建 廈門 361000)

一、引言與相關文獻綜述

黨的二十大報告指出,積極穩妥推進碳達峰碳中和需要堅持先立后破,有計劃分步驟地實施碳達峰行動。同時,實現“雙碳”目標要處理好“發展與減排的關系”以及“局部與整體的關系”。這意味著各地區不僅要優化經濟增長碳脫鉤狀態,保持經濟高質量發展(林伯強,2022),還需強化“全國一盤棋”意識,促進區域間低碳發展與節能減排的協同聯動(邵帥 等,2019)。“不謀全局者,不能謀一域”,各省份應當清晰認識其在全國經濟增長碳脫鉤狀態空間關聯網絡中的角色,提高碳脫鉤網絡的整體關聯性,形成合理的碳脫鉤空間布局(韓夢瑤 等,2021)。在此背景下,鑒別不同地區在經濟增長碳脫鉤關聯網絡中的角色及其碳脫鉤狀態傳遞方式,研究引致碳脫鉤空間關聯不同流向背后的作用機制和影響因素,有助于在綜合考量區域差異和關聯的基礎上,逐步優化經濟增長碳脫鉤狀態,科學有序推進碳達峰碳中和。

為了更好地揭示經濟增長與碳排放的同步變化規律,反映經濟發展范式綠色低碳化程度,越來越多的學者選擇Tapio脫鉤彈性系數法(Tapio,2007)測算地區經濟增長碳脫鉤狀態,從而揭露經濟增長與碳排放之間的動態關聯(夏勇,2017)。目前國內外關于地區經濟增長碳脫鉤狀態測算的文章已是汗牛充棟,大量研究表明不同地區之間的碳脫鉤狀態存在差異(Gupta,2015;李忠民 等,2010)。其中,部分學者認為地區間的碳脫鉤狀態差距正在不斷變大(張成 等,2013) ,但也有學者持相反觀點(鄧小樂 等,2016)。影響經濟增長碳脫鉤狀態的主要因素包括經濟規模、技術水平、能源強度、能源結構以及產業結構等(Zhu et al.,2017;Zhou et al.,2017;翁鋼民 等,2021)。隨著我國區域政策的不斷完善,各地區協調發展、同頻共振已成為經濟發展的“新常態”。在區域政策和市場機制的雙重推動下,要素流動、商品貿易以及其他經濟活動愈加頻繁,技術創新水平(張曦 等,2020)、經濟發展(李敬 等,2014)、能源強度(李博,2015)等影響經濟增長碳脫鉤狀態的各類指標呈現出密切的空間關聯關系與擴散效應,使得某一區域與另一區域在經濟增長碳脫鉤狀態上存在縱橫交錯、紛繁復雜的空間互動。張赫等(2022)認為,縣域經濟增長碳脫鉤狀態存在正向溢出的現象。翁鋼民等(2021)發現旅游業增長碳脫鉤狀態具有顯著的空間相關性和空間集聚效應。Zhou et al.(2023)研究發現相鄰地區的建筑業增長碳脫鉤狀態較為接近,換言之,碳脫鉤狀態可能存在空間溢出效應。綜合現有文獻,可以看出大多數研究僅停留在分析局部地區碳脫鉤狀態的演變及其影響因素層面,而從全局性視角深入探討區域間經濟增長碳脫鉤狀態空間關聯的研究卻寥寥無幾。相較于空間計量等統計學實證方法,社會網絡分析法可以更好地構建經濟增長碳脫鉤空間關聯網絡,進而揭示碳脫鉤狀態空間關聯的總體特征以及各區域在關聯網絡中的作用(Deng et al.,2022)。因此,本文首先采用社會網絡分析法構造經濟增長碳脫鉤狀態的空間關聯網絡,進而研究地區間經濟增長碳脫鉤狀態的空間關聯性,分析各地區在碳脫鉤網絡中所扮演的角色和發揮的作用,然后借助二次指派程序方法(Quadratic Assignment Procedure,QAP)考察碳脫鉤狀態空間關聯效應的影響因素。

與現有文獻相比,本文的貢獻主要體現在:(1)運用社會網絡分析法構建了我國省際經濟增長碳脫鉤空間關聯網絡,從而研究了區域間碳脫鉤狀態的聯動效應,以及碳脫鉤空間關聯效應的影響因素,推動了社會網絡分析法在碳脫鉤領域的應用。(2)將塊模型分析應用于經濟增長碳脫鉤領域研究,實證結果發現我國30個省份分別位于四個不同的功能板塊中,共同維系各地區碳脫鉤狀態的空間關聯性。(3)在碳脫鉤空間關聯模型的構建上做出了創新與改進。首先將不同程度的脫鉤狀態進行賦值處理(羅芳 等,2020),然后以賦值作為衡量碳脫鉤狀態的指標參與模型構建(杜之利 等,2021),避免了直接將脫鉤指數作為衡量指標可能導致的誤差(1)根據Tapio脫鉤分析法,判斷碳排放脫鉤狀態需要同時考慮經濟增長、碳排放增長以及脫鉤指數三個變量的符號與大小,若直接將脫鉤指數作為衡量脫鉤狀態的指標則會造成一定的誤差。。

二、模型構建與數據

(一)空間關聯網絡構建

社會網絡分析法是一種針對關系數據的跨學科分析方法,可以研究相關變量的空間關聯關系及其網絡特征(李敬 等,2014)。本文借鑒劉華軍等(2015)的做法,利用引力模型構建經濟增長碳脫鉤空間關聯網絡,碳脫鉤空間溢出效應的具體公式如下:

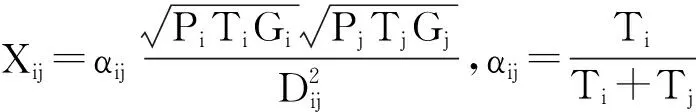
(1)

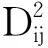
根據式(1),得到我國30省份(除西藏、港澳臺地區外)經濟增長碳脫鉤狀態的引力矩陣X=(Xij)30×30,再將引力矩陣進行“0-1”二值化處理,具體做法為:若某個元素大于該行的平均值,則記為1,表示該元素所在的行對應省份與所在列對應省份在碳脫鉤狀態上具有明顯的關聯關系;反之,記為0,表示不存在明顯的關聯關系。在此基礎上,將引力矩陣轉化為經濟增長碳脫鉤狀態的空間關聯網絡矩陣。

(二)空間關聯網絡的特征指標

1．整體網絡特征

刻畫整體網絡特征的指標有網絡密度(Dn)、網絡關聯度(Cn)、網絡等級度(Hn)以及網絡效率(En)。網絡密度(Dn)刻畫了一個群體所有成員之間的聯系程度,可表示為:

Dn=L/(N×(N-1))

(2)

其中,L代表空間關聯網絡中的關聯數量,N×(N-1)代表最大可能的關聯數,Dn取值范圍為0到1。網絡密度越大,代表網絡中不同主體之間的關聯性越強。

網絡關聯度(Cn)能夠刻畫網絡自身的穩健性和脆弱性,可表示為:

Cn=1-V/(N×(N-1)/

2)

(3)

其中,V表示沒有產生直接關聯的數量,Cn取值范圍為0到1。網絡關聯度(Cn)越大,各主體之間聯系越密切。

網絡等級度(Hn)反映了各成員產生相互關聯的難易程度,可表示為:

Hn=1-K/max(K)

(4)

其中:K表示對稱可達的點對數,即能夠互相產生溢出效應的點對數;max(K)表示最大對稱可達的點對數;Hn取值范圍為0到1。碳脫鉤網絡等級度越高,表明各主體之間產生關聯的難度越大。

網絡效率(En)刻畫了網絡中各成員的聯系效率,網絡效率越低,說明區域間存在越多的連線,溢出渠道越多,網絡也就越穩定,可表示為:

En=1-Mijmax(M)

(5)

其中,M代表網絡中存在的多余關聯數(兩個網絡主體之間產生關聯的過程中與其他主體的關聯數稱為多余關聯數),max(M)表示最大的多余關聯數。

2．個體網絡特征

各地區在網絡中的中心地位可以用度數中心度和中介中心度來衡量。度數中心度(De)指網絡中與某一區域直接相連的數目(用n表示)和最大可能直接相連的區域數目(用N表示)之比,度數中心度越高的地區,與其他省份的空間關聯程度越高,可表示為:

De=n/(N-1)

(6)

中間中心度(Cbi)越大的地區越靠近空間網絡結構的樞紐位置,對其他地區的空間關聯關系影響程度越大,可表示為:

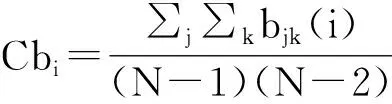
(7)

若一個區域處在多個區域相連接的路徑中,那么該區域在空間網絡中就處于一個重要的樞紐位置。假設區域j和k之間存在gjk條路徑,其中有gjk(i)條經過區域i,那么區域i對于區域j和k的重要性就可以用bjk(i)= gjk(i)/gjk表示。將區域i對于空間網絡中任意兩個區域的重要性相加,便可得到區域i的絕對中間中心度,將其標準化就是相對中間中心度(本文采用的是相對中間中心度)。

3．塊模型分析

塊模型分析可以用來探討碳脫鉤網絡中各個省份所在的位置(張輝 等,2019)。根據塊模型理論和各地區實際特征,將我國劃分成四個不同的板塊:“碳脫鉤凈受益”板塊、“碳脫鉤凈溢出”板塊、“碳脫鉤雙向溢出”板塊以及“碳脫鉤經紀人”板塊。其中:“碳脫鉤凈受益”板塊不但可以接收自身內部城市發出的經濟增長碳脫鉤關系,也可以接收其他板塊發出的經濟增長碳脫鉤關系,且接收的關系明顯多于發出的關系;“碳脫鉤凈溢出”板塊與之相反,其發出的關系明顯多于接收的關系;“碳脫鉤雙向溢出”板塊既可接收關系也可發出關系,但其接收的關系中,以自身內部發出的關系居多;“碳脫鉤經紀人”板塊與“碳脫鉤雙向溢出”板塊類似,但它們與其他板塊之間的聯系更多。

(三)QAP回歸模型構建

我國省際碳排放空間關聯呈現出網絡結構形態(Wang et al.,2018),且受到地理距離(Zhang,2017)、經濟發展水平(Ma et al.,2019)、能源強度(鄭航 等,2022)、技術水平(龐慶華 等,2019)、產業結構(王曉平 等,2020)、能源結構(趙桂梅 等,2020)等因素的影響。故本文選取以上六個指標作為影響碳脫鉤空間關聯效應的變量,構建如下QAP回歸模型:

T=f(D,P,I,S,E,R)

(8)

其中,D、P、I、S、E、R分別表示地理距離差異矩陣、經濟水平差異矩陣、產業結構差異矩陣、能源強度差異矩陣、能源結構差異矩陣、技術水平差異矩陣。各變量矩陣具體的衡量指標以及數據來源見表1。所有變量矩陣的元素均經過“0-1”二值化處理。

表1 變量含義以及衡量指標

(四)數據來源與描述性分析

1.數據來源

本文選取“雙碳”目標提出之前的2005—2019年我國30個省份(不包含西藏和港澳臺地區)作為樣本空間,構建碳排放脫鉤空間關聯網絡。相關數據來自《中國統計年鑒》《中國能源統計年鑒》及國家統計局,地理距離數據由Arcgis 軟件測算出。基于IPCC Guidelines for National Greenhouse Gas Inventories(2)http://www.ipcc-nggip.iges.or.jp/public/2006gl/vol2.html.提出的因素分解法,本文選取煤炭、原油、焦炭、燃料油、汽油、煤油、柴油、天然氣八種能源,測算出各地區二氧化碳排放量。

Tapio脫鉤分析法(Tapio,2007)引入彈性概念,通過簡單的數量關系表征經濟發展與污染物排放的關系,為定量描述經濟增長與碳排放的相互關系提供了全新視角(陸鐘武 等,2011)。基于Tapio脫鉤分析法,可測算出2005—2019年間我國各省份經濟增長與碳排放脫鉤狀態,具體表示如下:

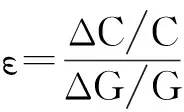
(9)

其中,ΔC為當期碳排放與前一期碳排放之差,C為前一期碳排放,ΔG為當期GDP與上一期GDP之差,G為前一期GDP。

借鑒Tapio(2007)、羅芳等(2020)對彈性值變化范圍的劃分,將碳脫鉤狀態類型劃分成強脫鉤、弱脫鉤、衰退脫鉤等八種,詳見表2。為便于計算經濟增長碳脫鉤狀態的空間關聯關系,本文將強負脫鉤、擴張負脫鉤、弱負脫鉤、衰退連接、擴張連接、衰退脫鉤、弱脫鉤、強脫鉤八種碳脫鉤狀態分別賦值為1～8分。

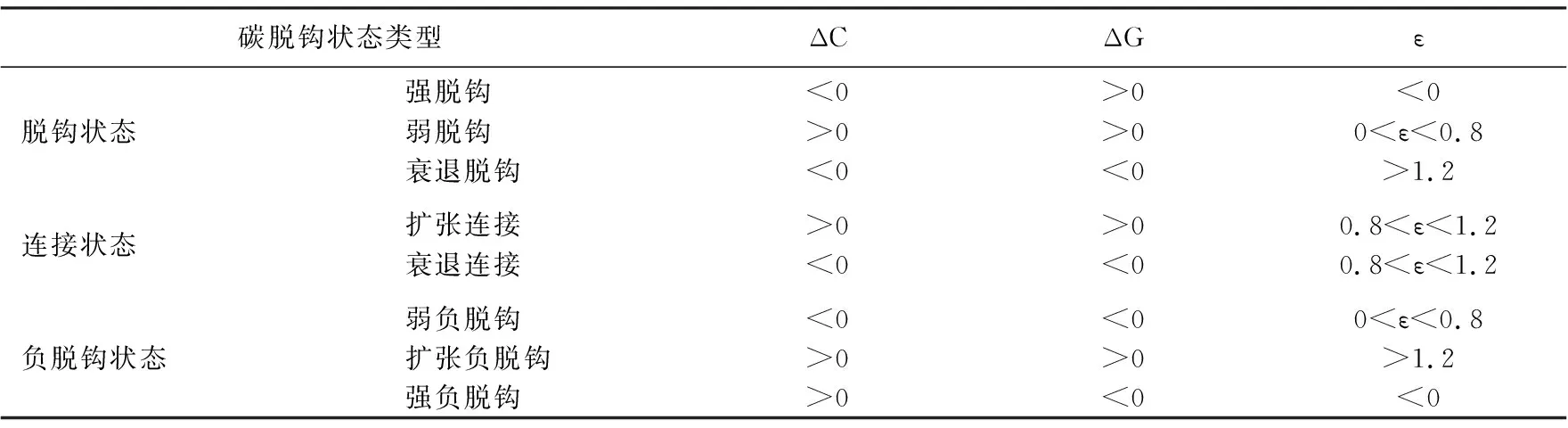
表2 經濟增長與碳排放脫鉤狀態類型

2.分地區碳脫鉤狀態描述性分析

按照地理位置,將我國30個省份劃分成東部、中部、西部三個區域,比較各區域2005—2009年、2010—2014年、2015—2019年三個時期經濟增長碳脫鉤的表現情況,結果如圖1所示。

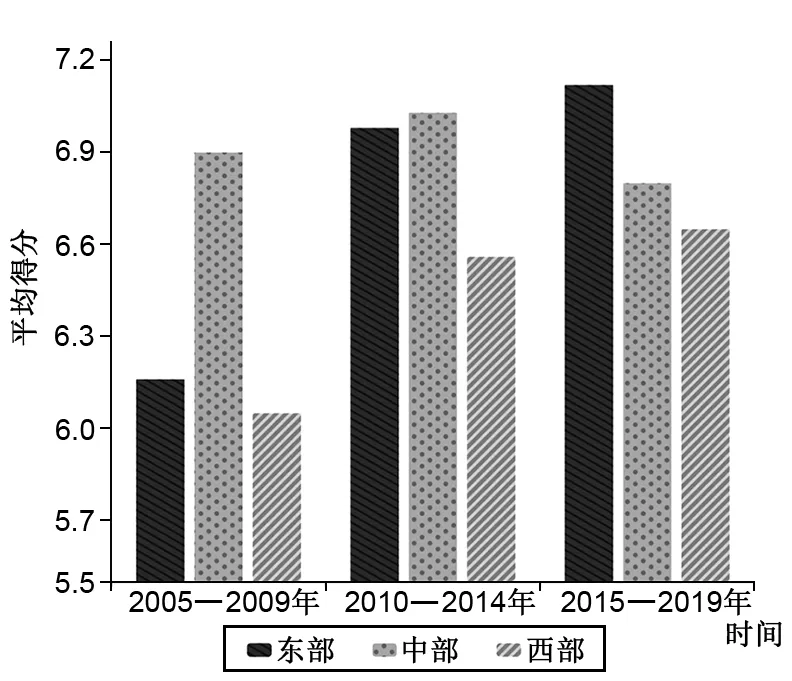
圖1 各區域經濟增長碳脫鉤狀態平均得分

由圖1可知,西部地區碳脫鉤狀態平均得分較低,這與新疆、內蒙古、陜西等省份經濟發展高度依賴于煤炭資源以及我國西部大開發政策導致碳排放重心向西北地區轉移有關(高長春 等,2016);中部地區碳脫鉤狀態平均得分呈現先上升后下降的趨勢,2010—2014年平均得分為7.08,但2015—2019年平均得分僅為6.80;東部地區的經濟增長碳脫鉤狀態整體上優于其他地區,原因在于東部地區的產業結構轉型升級進程領先于其他地區,高新技術產業、戰略性新興產業增加值增長較快,落后產能逐步被淘汰,轉方式調結構使得東部地區近些年的經濟增長碳脫鉤狀態明顯優化。

三、經濟增長碳脫鉤空間關聯網絡特征分析

(一)整體網絡特征及演變趨勢分析

經濟增長碳脫鉤空間關聯網絡結構分析包括三部分內容,即網絡結構形態分析、網絡密度與網絡關聯度分析、網絡效率與網絡等級度分析,分別從三個不同視角出發研究碳脫鉤整體網絡特征及其演變趨勢。從整體上看,我國各省份之間經濟增長碳脫鉤狀態的關聯網絡呈現出復雜化趨勢,以長三角地區為代表的標桿地區在我國綠色低碳高質量發展中充分發揮帶動作用,形成梯次帶動中西部地區綠色協調發展的新路徑。在堅持“全國一盤棋”原則實現“雙碳”目標的背景下,各地區產業協同轉型發展、環境協同治理、生態協同保護,使得經濟增長碳脫鉤狀態的相互溢出效應也隨之增強,即碳脫鉤關聯網絡變得更加復雜且高效。

1.經濟增長碳脫鉤的網絡結構形態分析

碳脫鉤網絡結構形態可以直觀反映不同地區在碳脫鉤網絡中所處的位置,以及與其他地區產生關聯的數量,包括溢出碳脫鉤關系數量和接受碳脫鉤關系數量,從而判斷該地區在整個碳脫鉤網絡中所發揮的作用。本文借助引力模型計算我國各省份經濟增長碳脫鉤的空間關聯關系,并在此基礎上構建經濟增長碳脫鉤空間關聯網絡,樣本區間為2005—2019年。圖2～4分別展示了2005年、2011年、2019年我國省際碳脫鉤網絡結構形態。可以看出,各地區之間經濟增長碳脫鉤狀態存在復雜的空間關聯關系,且關聯數量(圖中有向線段即表示空間關聯關系)隨時間逐漸增加,表明省際經濟增長碳脫鉤狀態的空間關聯性正在不斷提高。復雜的碳脫鉤網絡結構形態說明不同地區之間碳脫鉤狀態能夠打破地理間隔產生相互影響,同時也驗證了使用社會網絡分析方法的必要性。

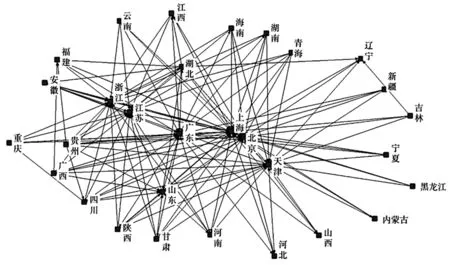
圖2 2005年經濟增長碳脫鉤狀態的空間關聯網絡

圖3 2011年經濟增長碳脫鉤狀態的空間關聯網絡

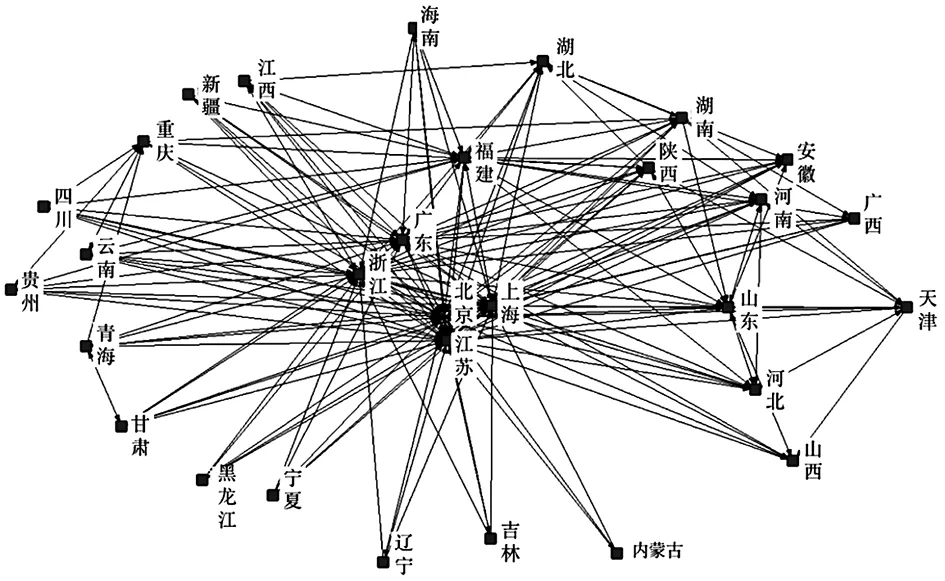
圖4 2019年經濟增長碳脫鉤狀態的空間關聯網絡

北京、上海、廣東、浙江等地長期位于空間關聯網絡中間,同時接受和發出大量碳脫鉤關聯關系;而吉林、新疆、青海、寧夏等地則處在空間關聯網絡邊緣,與其他省份的碳脫鉤關聯關系較少。原因可能在于,北上廣地區為我國重要的交通樞紐和經濟集聚中心(武文杰 等,2011),與各地的經貿往來、科研合作、人才交流等活動密切,從而間接影響其他地區經濟增長碳脫鉤狀態。具體而言,北京、上海等發達地區在交通碳排放效率關聯網絡、能源消費空間關聯網絡中處在核心主導地位,而吉林、寧夏等偏遠省份則處在絕對邊緣位置(邵海琴 等,2021)。與2005年相比,2019年碳脫鉤空間關聯網絡中位于網絡邊緣的省份(如新疆、寧夏、陜西等地)與其他地區的關聯數量明顯變多,原因可能在于交通等基礎設施的逐漸完善促進了省際要素流動,同時各省份的商貿往來、科技交流等活動更加頻繁,進而增強了經濟增長碳脫鉤狀態的區域聯動性。綜上,一方面,我國省際經濟增長碳脫鉤空間關聯網絡的結構形態隨著時間推移變得愈加復雜,說明碳脫鉤空間聯動效應正在不斷加強,這也證明了我國堅持“全國一盤棋”實現碳中和的必要性。另一方面,北上廣等發達地區長期位于脫鉤網絡中心位置,與各地區碳脫鉤狀態聯系緊密;而寧夏、新疆等邊遠地區雖處在脫鉤網絡的邊緣地位,但碳脫鉤關聯數量逐年增加,同其他省市的交流正在不斷加強。

2.經濟增長碳脫鉤的網絡密度與網絡關聯度分析

碳脫鉤網絡關聯數代表脫鉤網絡中不同主體碳脫鉤狀態相互溢出的關系數量,網絡密度則是網絡關聯數占最大可能關聯數的比值,反映碳脫鉤網絡整體關聯性強弱。網絡關聯數和網絡密度越大,網絡中不同主體間的空間關聯性越強。本文測算了我國各地區經濟增長碳脫鉤空間關聯網絡的關聯數量以及網絡密度的時空演變趨勢,結果如圖5所示。同時,2005—2019年碳脫鉤網絡關聯度的測算結果均為1,表明我國各地區碳脫鉤狀態之間存在密切的空間關聯。

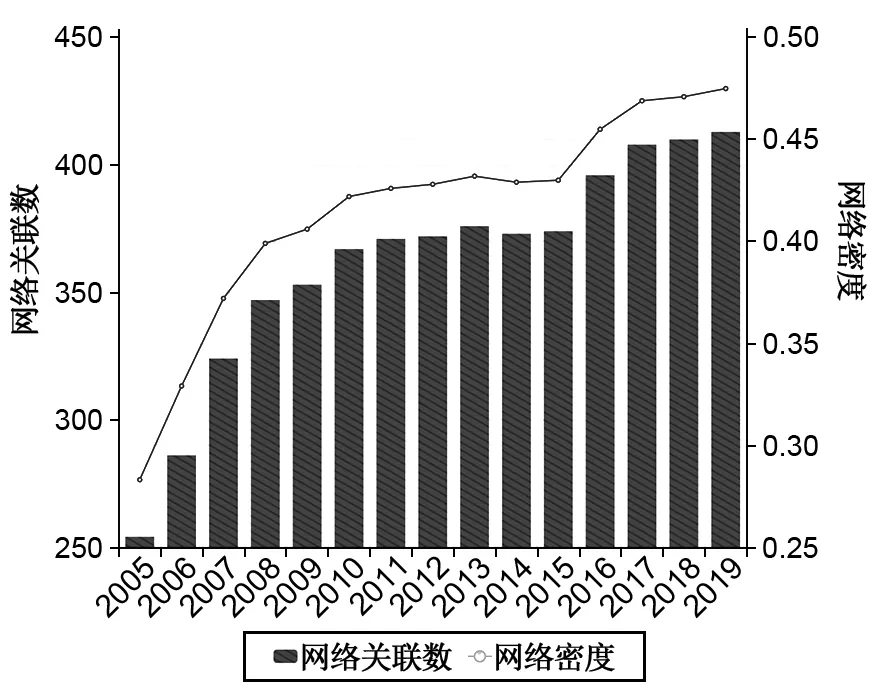
圖5 網絡關聯數與網絡密度

網絡關聯數與網絡密度的變化趨勢保持一致,且可以分為三個階段:2005—2008年網絡關聯數與網絡密度的增長速度較快,2009—2015年變化趨勢不明顯,2016—2019年又表現出顯著的上升趨勢。同時脫鉤狀態的網絡關聯數最高也才達到408,遠低于30個地區最大關聯關系數870(30×29),表明我國各地區經濟增長與碳排放脫鉤狀態的整體空間關聯性水平不高,需要進一步加強各地區間關聯性,助力“全國一盤棋”實現碳中和目標。此外,樣本期內的網絡密度平均值只有0.415,表明各地區經濟增長碳脫鉤狀態的空間關聯關系不夠緊密,省際交流仍需要進一步加強。

3.經濟增長碳脫鉤的網絡效率與網絡等級度分析

通俗來講,網絡效率就是各地區之間經濟增長碳脫鉤狀態相互溢出的快慢,網絡等級度反映出不同地區碳脫鉤狀態溢出的難度。結構越復雜的空間網絡其網絡效率越低,而網絡等級度越低越有利于碳脫鉤狀態產生空間關聯關系,使得網絡中碳脫鉤關聯數量增加,導致碳脫鉤網絡結構變得更加復雜。

2005—2019年經濟增長碳脫鉤空間關聯網絡的網絡效率與網絡等級度見圖6。可以看出,網絡效率表現出波動減小的趨勢,在2010年和2018年出現顯著下降,這表明經濟增長碳脫鉤空間網絡的關聯性在逐步提高,整體網絡的穩定性不斷上升。

圖6 網絡等級度與網絡效率

網絡等級度反映不同地區間存在的空間等級制度,等級制度越高,各地區之間產生相互影響就越難(曹薇 等,2019)。由圖6可知,我國省際經濟增長碳脫鉤狀態的網絡等級度呈現出下降的趨勢,說明地區間固有的等級制度逐漸被打破,省際的空間交互作用正不斷擴大。網絡等級度與網絡效率在2005—2019年間存在較強的波動性,其原因可能是:不同地區間存在明顯的經濟發展梯度,低碳綠色工業化水平差距較大,區域間的不平衡會導致低碳產業布局以及減排步伐不一致的局面,從而影響地區間碳排放脫鉤狀態相互溢出的難易程度,表現在省際網絡等級度在整體下降趨勢中伴隨著較強的波動。

(二)個體網絡結構特征及演變趨勢分析

本文測度了2005—2019年間碳脫鉤空間關聯網絡個體特征及其演變趨勢,具體指標為受益關聯關系、溢出關聯關系、度數中心度、中間中心度,以揭示各地區在碳脫鉤狀態空間關聯網絡中的定位和作用。圖7展示了2019年我國七大區域(3)根據地理位置將我國各省份劃分為華北、東北、華東、華中、華南、西南、西北七大區域。各指標測算結果。

圖7 受益(溢出)關聯關系數、度數(中間)中心度

受益關系數是指收到其他地區碳脫鉤狀態關聯關系數量,溢出關系數代表該地區向外發出的碳脫鉤狀態關聯關系數量(張正峰 等,2023)。總體上看,東部沿海地區的受益關聯數量明顯大于溢出關聯數量,而中西部地區溢出關聯數量明顯普遍高于受益關聯數量。

度數中心度和中間中心度衡量的是碳脫鉤空間關聯網絡的中心性結構。度數中心度越高的地區與其他地區碳脫鉤的關聯程度越大。由圖7可知,華東、華南區域度數中心度較高,說明該區域內省份和其他地區的碳脫鉤空間關聯關系較為密切,這與張德鋼等(2017)的研究結果相似。究其原因,華東、華南區域省份均為我國經濟水平、科技發展水平較為發達或者人口、勞動力較為密集的地區,在科技、教育、文化、衛生等領域與其他地區存在較多空間關聯關系,與其他地區在碳排放脫鉤、經濟綠色轉型等方面溝通的障礙較少。北京、上海、廣東、江蘇等地科技創新能力較強,能源效率較高,吸引了大量的創新要素集聚,表現出“孔雀東南飛”的現象(劉和東,2013),因此這些地區能夠與其他地區產生密切的關聯,處在碳脫鉤網絡的樞紐位置。山東、湖南等地年末常住人口位居全國前列,勞動力資源豐富,勞動力流動使其與各地的聯系更加緊密,而技能型勞動力集聚則對地區減排存在顯著影響(赫永達 等,2022)。由此可見,經濟發展水平、科技創新能力以及勞動力流動等因素對于省際經濟增長與碳排放脫鉤狀態的空間關聯性具有重要影響。

中間中心度越大的地區越靠近碳脫鉤網絡的樞紐位置,與其他地區進行碳脫鉤狀態交流的能力越強。從圖7可知,華北、華東、華南地區的中間中心度較高,如廣東、北京、江蘇、上海等,這些地區與其他地區進行碳排放脫鉤狀態交流的效率更高,處在關聯網絡的樞紐位置。這與童磊等(2020)的研究結果相似,其同樣發現這些地區處在我國碳排放空間關聯網絡的中心樞紐位置,扮演著重要的“中介”角色。同時,從整體上看,中間中心度呈現出明顯的空間非均衡特征,排名前列的地區控制著網絡中絕大部分的空間聯系,而其他地區如西北、西南地區寧夏、新疆、貴州、云南等地,處在“被支配”的邊緣地位,主要原因在于地理位置偏遠且交通設施不夠完善。

(三)經濟增長碳脫鉤的塊模型分析

本文采用迭代相關收斂法將復雜網絡簡化為塊模型實現網絡的聚類分析。參考王小華等(2022)的做法,選擇最大分割深度為2,收斂標準為0.2,將30個省份劃分成四個板塊。四個板塊具體的接受關系數和發出關系數結果如表3所示。

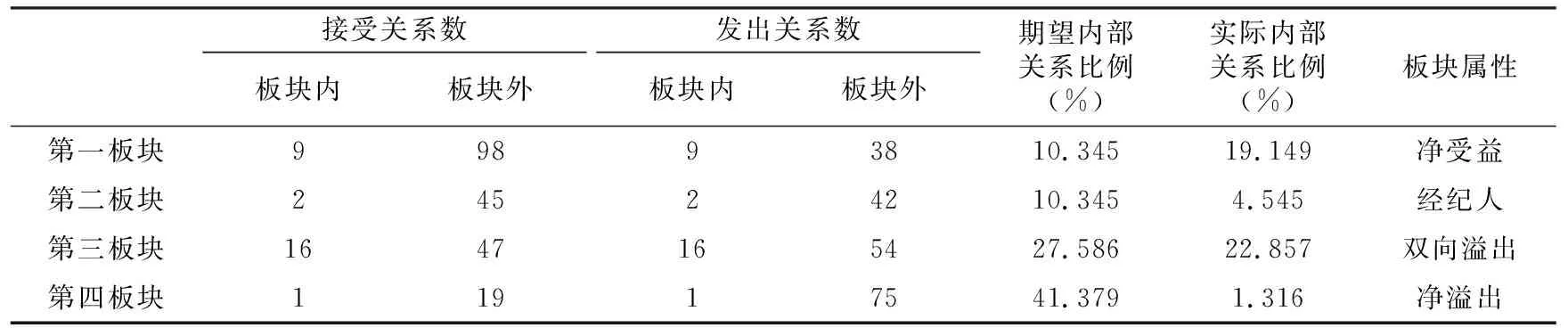
表3 2019年省際經濟增長碳脫鉤狀態空間關聯板塊的溢出效應

第一板塊接受關系總數為107個,其中板塊內9個,板塊外98個;發出關系總數為47個,其中板塊內9個,板塊外38個。該板塊既接受關系也發出關系,且接受關系數明顯大于發出關系數,故第一板塊屬性為“碳脫鉤凈受益”板塊。該板塊包括北京、上海、江蘇、浙江等省份,經濟發達但自身資源相對匱乏,需要接受來自其他地區能源等生產要素的輸入,如“西氣東輸”“西電東送”工程等。因此,可以認為第一板塊各地區在整體網絡中表現為“碳脫鉤凈受益”角色。

第二板塊接受關系總數為47個,其中板塊內2個,板塊外45個;發出關系總數為44個,其中板塊內2個,板塊外42個。該板塊既接受關系也發出關系,但在接受關系中與其他板塊關聯更多,因此確定第二板塊屬性為“碳脫鉤經紀人”板塊。該板塊包括天津、福建、廣東、重慶等省份,其度數中心度均在全國排名前列,表明這些地區與其他地區相互關聯的效率更高,在空間關聯網絡中扮演著“中介”的角色,這也與第二板塊“碳脫鉤經紀人”屬性相符。

第三板塊接受關系總數為63個,其中板塊內16個,板塊外47個;發出關系總數為70個,其中板塊內16個,板塊外54個。該板塊既接受關系也發出關系,且其接受關系中以內部發出的關系居多,因此第三板塊屬性為“碳脫鉤雙向溢出”板塊。該板塊包括9個省份(河北、山西、安徽、江西、山東、河南、湖北、湖南、陜西),主要是以農林牧業、傳統工業等為支柱產業的地區,這些地區對板塊內地區發出關系的數量與其接受來自其他地區關系的數量差距相對較小,因此表現出“雙向溢出”屬性。

第四板塊接受關系總數為20個,其中板塊內1個,板塊外19個;發出關系總數為76個,其中板塊內1個,板塊外75個。該板塊既接受關系也發出關系,且發出關系數明顯大于接受關系數,因此確定第四板塊屬性為“碳脫鉤凈溢出”板塊。該板塊包括內蒙古、遼寧、吉林、黑龍江、廣西、海南、四川、貴州、云南、甘肅、青海、寧夏、新疆等省份,主要為能源資源豐富或生態資源豐富的中西部地區,蘊藏豐富的風電和太陽能資源(徐斌 等,2019)。西北、華中地區為清潔能源主要的輸出端,而華東地區為受能端(林伯強 等,2022),故第四板塊在經濟增長碳脫鉤狀態空間關聯網絡中扮演“碳脫鉤凈溢出”角色。

四、經濟增長碳脫鉤空間關聯關系影響因素分析

本文基于二次指派程序(QAP)研究經濟增長碳脫鉤關聯關系的影響因素。QAP分析法包括相關性分析與回歸分析。其中,QAP相關性分析可以驗證不同矩陣變量之間存在多重共線性;若不同變量之間存在多重共線性,則需要進一步使用能夠解決多重共線性問題的QAP回歸分析方法,再對其相關系數進行非參數檢驗(Everett,2002)。

(一)QAP相關性分析

首先采用QAP相關性分析考察被解釋變量矩陣,即碳脫鉤空間關聯矩陣和地理距離矩陣、經濟水平差異矩陣等6個影響因素矩陣之間的相關關系。參考李敬等(2014),本文選擇5000次隨機置換,得到的結果如表4所示。表4中的實際相關系數根據兩個矩陣的具體數值計算得出,相關系數均值根據5000次隨機置換計算得出,最大值、最小值是隨機置換計算出的最大和最小相關系數,P≥0表示隨機置換計算出的相關系數大于或等于實際相關系數的概率,P≤0表示隨機置換計算出的相關系數小于或等于實際相關系數的概率。

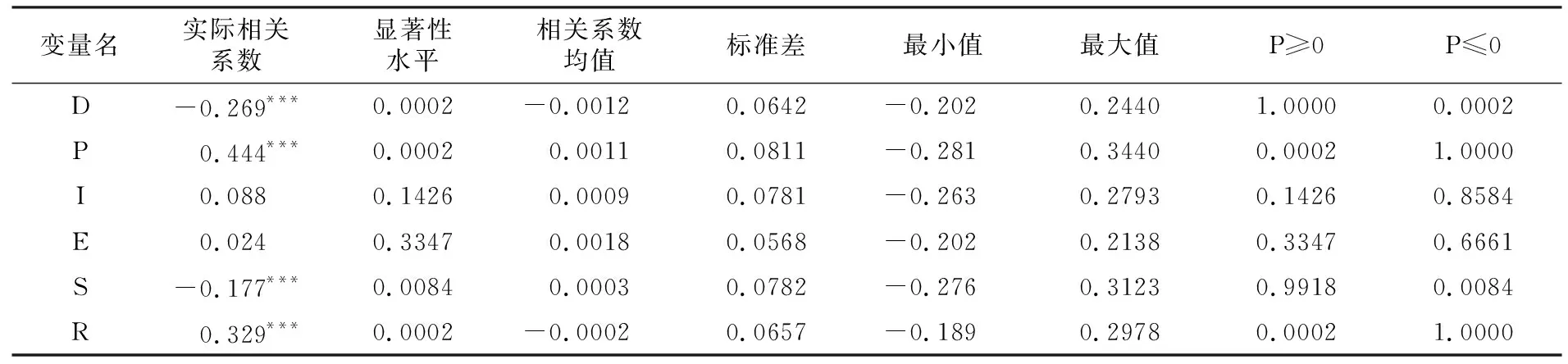
表4 空間關聯矩陣T與其他影響因素矩陣的QAP相關性分析結果

QAP相關性分析結果表明,碳脫鉤空間關聯矩陣T與地理距離矩陣D的相關系數在1%水平上顯著為負,說明地理距離對于碳脫鉤狀態空間溢出效應確實存在顯著的負向影響。能源強度矩陣S與空間關聯矩陣T的相關系數在1%水平顯著為負,但是相關系數小于地理距離矩陣D與空間關聯矩陣T的相關系數,說明其對空間溢出的影響相對弱一些。經濟水平矩陣P、技術水平矩陣R與空間關聯矩陣的相關系數較大,且均在1%水平上顯著為正,說明二者對于脫鉤狀態的影響較為突出,經濟水平發達、技術水平先進的地區其碳排放脫鉤狀態對于其他地區的溢出效應更大。經濟發展動力逐步轉向技術進步程度更高、以信息通信技術為主導的低碳產業,進入低碳發展軌道(孫傳旺 等,2022),因此在實現“雙碳”目標過程中應該重視這些地區的經濟增長碳脫鉤狀態。產業結構矩陣I、能源結構矩陣E與碳脫鉤空間關聯矩陣T的相關系數較小且不顯著,說明產業結構與能源結構對于碳脫鉤狀態的溢出效應作用不明顯,與Zhang et al.(2015)的研究結論一致。

進一步對與碳脫鉤空間關聯矩陣顯著相關的四個變量矩陣進行相關性分析,發現地理距離矩陣D、經濟水平矩陣P、技術水平矩陣R以及能源強度矩陣S之間兩兩存在顯著的相關性(4)篇幅所限,結果未詳細列示,留存備索。。這說明上述四個變量矩陣對于碳排放空間關聯矩陣的影響可能存在重疊性,需要采用QAP回歸分析才能較好處理多重共線性問題。這也驗證了本文采用QAP回歸分析的必要性(王曉平 等,2020)。

(二)QAP回歸分析

QAP回歸分析的目的在于研究一個變量矩陣與多個變量矩陣之間的回歸關系,其過程分為兩步:首先,對所有變量矩陣對應的長向量元素進行一般的多元回歸分析;其次,對因變量矩陣各行各列進行隨機置換處理,再重復上一步,計算多元回歸的結果。當這兩步重復足夠多次數后,便可以估計統計量的標準誤。相關系數的估計和檢驗方法與QAP相關性分析一致。

本文采取QAP回歸分析,選擇5000次隨機置換,得到我國經濟增長碳脫鉤狀態空間關聯矩陣T與影響因素矩陣(地理距離矩陣D、經濟水平差異矩陣P、能源強度差異矩陣S、技術水平差異矩陣R)的QAP回歸分析結果,具體如表5所示。概率1、概率2分別表示5000次隨機置換過程中4個解釋變量的回歸系數大于等于、小于等于實際觀察到的回歸系數的概率值,進行的是雙尾檢驗。模型決定系數R2和調整后R2的值分別為0.344和0.341,說明四個變量矩陣可以解釋碳排放脫鉤狀態空間關聯關系變異的34.1%。P值是隨機置換產生的決定系數不小于實際觀察值的概率,為單尾檢驗的概率。P值為0,說明調整后R2在1%水平上顯著。考慮到30個省份的空間關聯矩陣為30行30列的矩陣,忽略對角線的元素,可得30×(30-1)=870個樣本數。

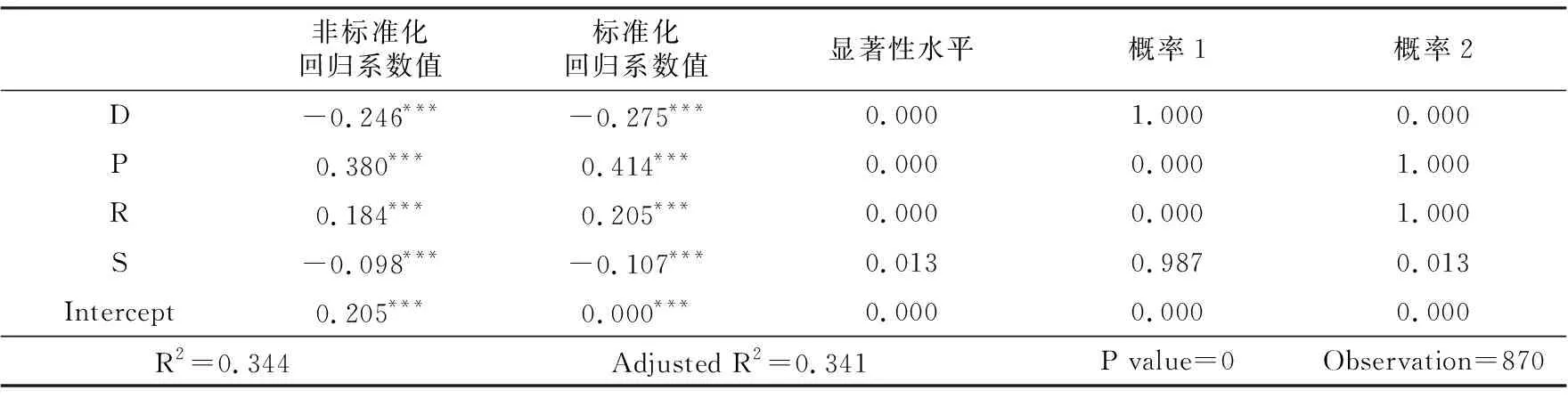
表5 空間關聯矩陣T與影響因素的QAP回歸分析結果

表5結果顯示,地理距離矩陣D、經濟水平差異矩陣P、能源強度差異矩陣S以及技術差異矩陣R四個解釋變量的標準化回歸系數均在1%水平上顯著,說明這四個變量對于省際經濟增長碳脫鉤狀態的空間關聯關系具有重要作用,與 Liu et al.(2021)的研究結論相似。地理距離變量矩陣D與能源強度變量S的回歸系數為負,說明其對于碳脫鉤狀態的溢出效應存在抑制作用。相鄰地區之間的經濟互動往往更加頻繁,進而使得經濟增長碳脫鉤狀態的關系更緊密,碳中和能力存在空間溢出效應(杜鵬程 等,2022)。經濟增長碳脫鉤狀態與碳中和能力密切相關,因此,地理位置上鄰近的地區間碳脫鉤狀態關聯性也會更強。能源強度差異矩陣S的回歸系數為負,表明兩個地區之間能源強度差異越小,碳脫鉤的空間聯動性越強。經濟水平差異矩陣P與技術水平差異矩陣R的回歸系數為正,說明經濟水平、技術水平的差距越大,碳脫鉤狀態的溢出效應越強。經濟發展水平較高、技術先進程度更高的地區對較落后地區的經濟發展模式、技術水平能夠產生顯著的積極影響,原因在于欠發達地區會借鑒國內發達地區的發展模式,并加強與其科技創新交流等從而提高自身的技術水平。同時,經濟發展水平、技術水平是影響碳排放脫鉤狀態的重要因素(寧亞東 等,2017),對區域低碳發展具有顯著的促進作用(王玉娟 等,2021),因此經濟發展水平差異、技術水平差異對于碳脫鉤狀態空間關聯性具有正向影響效應。

五、結論與政策建議

本文在傳統社會網絡分析法基礎上創新模型構建方法,探究了我國碳脫鉤空間關聯網絡的結構特征以及演變趨勢等,并且將二次指派程序(QAP相關性分析、QAP回歸分析)應用于經濟增長碳脫鉤狀態空間關聯性的研究。具體結論包括:(1)整體上,我國各省份經濟增長碳脫鉤狀態存在顯著的區域差異性,東部地區優于中、西部地區,且各地區碳脫鉤狀態整體上呈現出上升的趨勢。(2)經濟增長碳脫鉤狀態的空間關聯關系數量在逐年增加,但相對于最大可實現的空間關聯關系數量仍處于較低的水平,各區域間的總體緊密程度不高。同時,網絡的穩定性在不斷變強,體現在碳脫鉤狀態網絡等級度和網絡效率均呈現出下降的趨勢。(3)各省份在碳脫鉤關聯網絡中扮演著不同的角色。通過中心性分析,本文發現北京、上海、廣東三個地區長期處于碳排放脫鉤空間關聯網絡中心位置,而部分偏遠省份處在碳脫鉤網絡的邊緣位置。(4)碳脫鉤空間關聯網絡可以劃分為四個不同的功能板塊,即“碳脫鉤凈受益”板塊、“碳脫鉤經紀人”板塊、“碳脫鉤雙向溢出”板塊,以及“碳脫鉤凈溢出”板塊。(5)地理距離、能源強度水平差異對于經濟增長碳脫鉤狀態的空間關聯性具有顯著的負向影響效應,而經濟水平差異、技術水平差異可以有效提高碳脫鉤狀態的空間關聯性。

基于以上結論,本文提出如下政策建議:(1)系統把握經濟增長碳脫鉤空間關聯網絡,協同優化經濟增長碳脫鉤狀態,促進不同地區間的要素流動、科技交流、商貿往來等活動,提高碳脫鉤狀態的空間聯動效應。(2)充分發揮中部地區各省份“碳脫鉤經紀人”角色的“中介”作用,提高省際多邊科學合作,加快構建新型能源體系,實現能源結構低碳轉型,提升可再生能源消納能力。(3)加快完善全國性碳交易市場的建設,通過市場的手段引導高耗能行業實現能源結構轉型,降低傳統化石能源的使用比例,進而縮小地區間能源強度差距,提高經濟增長碳脫鉤空間關聯性。