采用知識遷移加速的智能氣動設計優化方法

郭振東,李存晰,宋立明,李軍,豐鎮平

(西安交通大學能源與動力工程學院,710049,西安)

氣動形狀優化作為飛機翼型和航空發動機葉片設計的重要環節,一直是國內外學者研究和關注的重點[1-4]。飛機翼型和航空發動機葉片的形狀多采用自由曲線/曲面設計,由于設計時輸入設計參數與輸出目標性能之間的函數關系無法用顯式表達[5],且氣動性能評估通常非常耗時,所以是典型的昂貴黑盒子問題[6]。通常,氣動形狀優化包括3個關鍵環節,即氣動形狀設計空間參數化、優化算法和性能評估。常用的參數化方法包括非均勻有理B樣條(non-uniformed rational B-spline,NURBS)法、自由網格形變 (free-form deformation,FFD)法等[7]。近年來,基于深度學習的智能參數化方法如 Bezier-GAN法[8]、AirfoilGAN法[9]等亦被提出用于翼型參數化建模。在確定氣動形狀設計空間后,代理模型優化算法等全局類優化算法被廣泛用于氣動設計空間尋優[10-11],而計算流體動力學 (computational fluid dynamics,CFD)方法則被用于對優化個體進行性能評估。

隨著氣動形狀設計要求的不斷提高,精細氣動形狀設計優化面臨如下困境:一方面,為滿足日益苛刻的性能指標要求,設計人員往往會增加參數化設計空間的維度,以期實現更精細的氣動型線調整,囊括性能更優的設計樣本[12],但隨著設計空間變量維度的增加,采用全局類優化算法探尋設計空間最優解所需樣本的評估次數將以指數形式急劇增加[10-13];另一方面,日益精細的氣動形狀設計通常采用非定常計算等更高精度的CFD評估手段對飛機翼型、航空發動機葉片進行性能評估[14-15],而非定常計算等高精度評估方法相對于傳統常用的定常計算,所需的計算資源急劇增加,在規定的任務周期內所能容許的高精度性能評估次數非常有限。為此,如何平衡上述兩個方面的矛盾,即如何縮短“精細化設計優化所需的最少性能評估次數”與“任務周期內所能容許的最大性能評估次數”之間的差距,是當前氣動形狀設計優化方法研究無法回避的難題。

另外需要特別指出的是,在當前絕大多數氣動形狀設計優化過程中,當優化目標和參數化設計空間確定后,優化算法往往“從零開始”對設計空間尋優。與此類傳統優化方法不同的是,設計人員通常能不斷地從已完成的任務中提取經驗,用于指導新任務的求解[16-17]。受到上述啟發,“知識遷移”理念在機器學習及計算智能領域得到了廣泛關注,相關研究又被稱為“遷移學習 (transfer learning)”[17]和“遷移優化 (transfer optimization) ”[18-19],其核心思路是讓機器學會像人一樣累積經驗,從已完成的類似任務中智能汲取有用信息,用于減少目標任務求解成本,并進一步提升目標任務優化解性能。

近年來,知識遷移理念在航空發動機設計領域亦受到重視[20-21],Rolls-Royce研究團隊已著手于將知識遷移理念用于航空發動機總體設計建模,測試結果表明相對于傳統方法,采用知識遷移策略可將設計效率提升80%[22]。然而,將知識遷移理念推廣到飛機翼型、航空發動機葉片形狀的設計優化時,仍需解決如下兩個方面的問題:①如何將已完成的類似任務優化解集編碼至目標任務參數化設計空間,即如何將已采用NURBS、FFD及Bezier-GAN等不同方法進行參數化建模的已完成任務優化解編碼至目標任務參數化設計空間;②如何提取已完成任務樣本中所包含的有用設計信息,用于促進目標優化任務的求解。

針對以上兩方面問題,本文采用深度學習模型變分自編碼器(variational autoencoder,VAE)[23],將已完成的相關任務優化解集編碼至目標任務參數化設計空間;接著,采用多保真度高斯過程[24-25]從已完成任務的樣本中提取有用信息,促進目標任務的求解;最后基于上述思路,建立了氣動形狀遷移優化方法,并通過基準數值算例開展測試與翼型氣動型線優化分析,驗證了知識遷移策略的有效性。

1 遷移優化簡介

如圖1所示,遷移優化的基本思路即讓優化算法像人一樣累積經驗,從已完成的相關任務S1,…,Sm中汲取有用信息,并形成知識庫K(t),用于指導目標任務T的求解[18]。相應的目標優化任務表達式可表示如下

(1)

(2)

除經典的遷移優化方式外,在同一問題的不同形式間相互汲取有用信息的多平臺遷移優化亦被提出,其原理如圖2所示。多平臺遷移優化原理的基本思路為尋找可對目標任務T進行簡化的問題T1,…,Tk,和目標任務T一起求解,并在優化過程中不斷從T1,…,Tk以及T中提取有用設計信息,形成知識庫K(t),以促進各任務的求解,最終實現提高目標任務T的優化效率。其相關表達式如下

(3)

圖2 多平臺遷移優化原理示意圖Fig.2 Schematic of multi-form transfer optimization

2 知識遷移加速的氣動設計優化方法

采用知識遷移加速的智能氣動設計優化方法包括兩個環節:氣動形狀設計空間參數化和遷移優化算法。下面將在2.1節和2.2節對所提出的采用VAE模型的氣動形狀參數化方法與貝葉斯遷移優化算法進行介紹,進而在2.3節對所發展的氣動型線遷移優化設計框架進行說明。

2.1 采用VAE模型的形狀參數化方法

圖3 VAE模型氣動形狀參數化方法原理圖Fig.3 Schematic of VAE-based aerodynamic shape parameterization method

在傳統的設計優化過程中,設計人員往往采用NURBS、FFD等方法獲得低維參數化設計空間ζ,進而在ζ空間開展型線優化設計。在完成型線優化設計后,設計人員往往會保留以散點坐標表征的真實型線樣本x及其性能分析結果文件,卻很少保留對應的低維參數化空間樣本z。然而,NURBS、FFD等傳統參數化方法無法實現從x→z的轉換,即很難將已完成任務所獲得的優秀型線樣本編碼至目標任務參數化設計空間。當且僅當已完成任務與目標任務樣本可用相同的FFD、NURBS參數化空間表示時,已完成任務樣本才能被用于目標任務設計過程,這嚴重限制了遷移優化策略在氣動型線設計優化中的應用。

2.2 貝葉斯遷移優化TGO算法

在建立VAE參數化設計空間實現了將已完成任務樣本統一編碼至目標任務參數化空間后,仍需解決如何提取已完成任務樣本中的有用信息用于加速目標任務的優化進程這一問題。為此,在貝葉斯優化框架下,將基于多保真度高斯過程的序列遷移優化策略與多平臺遷移優化策略相結合,研發了貝葉斯遷移優化算法 (transfer learning accelerated efficient global optimization,TGO)。以下將對TGO算法所采用的遷移優化策略及其優化流程進行介紹,并應用算例進行測試。

2.2.1 基于多保真度模型的序列遷移優化

在目標任務參數化設計空間中,假定已完成任務樣本集為{zS,yS}m,目標任務樣本為{zT,yT}n。基于多保真度模型的序列遷移優化策略的基本思路為,將{zS,yS}m作為目標任務的低保真度樣本,利用多保真度高斯過程將{zS,yS}m與{zT,yT}n進行數據融合。上述過程能有效地提高貝葉斯尋優代理模型的預測精度,特別是代理模型在最優值鄰域內的預測精度,由此加速目標任務優化進程。

參照原始模型推導過程[26],用于融合{zS,yS}m與{zT,yT}n的多保真度高斯過程預測模型可表示如下

(4)

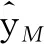
在構建多保真度代理模型的基礎上,通過最大化期望提升(expected improvement,EI)函數對目標函數設計空間進行貝葉斯尋優,其具體表達式如下

(5)

式中:yPBS為當前所獲得的最優目標函數值;Φ(·)和φ(·)分別為高斯累積分布函數和密度分布函數;σM(z)為多保真度高斯過程在z處目標函數預測值的標準差。

2.2.2 多平臺遷移優化與TGO算法流程

在優化后期,隨著目標任務樣本增加,直接采用目標任務樣本構建的單保真度代理模型精度可能會比融合已完成任務、目標任務樣本所構建的多保真度代理模型精度更高[24]。為盡可能提高用于貝葉斯尋優的代理模型精度,進而加速目標任務求解,在圖2所示多平臺遷移優化思想的啟發下,提出同時開展基于單保真度模型和多保真度模型的設計空間尋優。直接采用目標任務樣本{zT,yT}n所構建的單保真度預測模型表達式如下[26-27]

(6)

在完成單保真度代理模型構建后,通過最大化EI函數進行設計空間尋優,表達式可寫為

(7)

由于同時進行單保真度與多保真度代理模型尋優,在多保真度框架下每次優化迭代將更新2個樣本,相關表達式如下

(8)

式中Znew為每步迭代將采樣的個體。

圖5給出了本文所提出TGO算法的流程圖。其中,實線方框對應傳統無知識遷移的經典代理模型優化(efficient global optimization,EGO) 算法的執行流程,即僅利用目標任務樣本{zT,yT}n構建單保真度代理模型,進而基于式(7)進行設計空間尋優。在EGO算法的基礎上,TGO算法融入了基于多保真度代理模型的尋優過程,開展針對同一優化問題的“多任務”尋優過程,并在每次優化結束時,通過交換最優解,用于單、多保真度模型更新,來實現“多任務”信息交換,達到提升優化效率的目的。

圖5 本文所提出TGO算法流程Fig.5 Flowchart of TGO algorithm

2.2.3 數值算例測試

鑒于遷移優化與多保真度優化的相似性,選取經典的多保真度優化基準測試算例,對TGO算法的有效性進行測試,相關函數表達式如表1和表2所示。可以看到,多保真度優化測試中采用的低保真度函數被當作了遷移優化測試的已完成任務函數。

表1 用于TGO算法測試的目標任務與已完成任務表達式

表2 測試函數表達式

由于在實際場景中,已完成任務樣本{zS,yS}m的設計空間分布特征無法事先確定,為模擬上述情形,對表1所示已完成任務樣本開展貝葉斯優化,將優化完成時所生成的樣本集作為{zS,yS}m的候選數據庫。此外,注意到用于遷移優化的多保真度建模的核心任務,是利用已完成任務與目標任務的相似性,提高用于貝葉斯尋優的代理模型在設計空間最優值鄰域內的預測精度。為此,借鑒Wang等遷移優化研究經驗[21],采用最優解準則篩選出已完成任務樣本用于TGO優化,即根據目標函數對已完成任務樣本進行排序,選取性能最優的數十個樣本,用于TGO算法中的多保真度建模過程。

對基準測試函數分別開展10次測試計算,圖6分別展示了TGO和EGO算法的均值收斂圖,表3展示了10次優化所獲得的最優解均值及標準差。易見,相較于傳統無知識遷移的EGO算法,TGO算法收斂速度更快,獲得的優化解更優,且10次優化的最優解均值和標準差均顯著小于EGO算法,由此驗證了所提出的采用知識遷移加速的TGO算法的有效性。

(a)基準函數1

(b)基準函數2

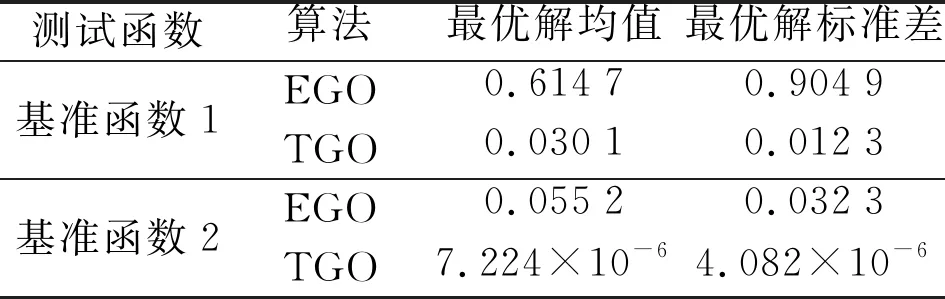
表3 2種算法的基準函數算例測試結果

2.3 采用知識遷移加速的設計優化框架VAE-TGO方法

將基于VAE的形狀參數化方法與TGO算法相結合,研發了氣動型線遷移優化框架,并將其命名為VAE-TGO方法,如圖7所示。VAE-TGO方法的基本流程如下:首先收集型線樣本,構建基于VAE的型線參數化模型;然后基于VAE解碼器,在VAE低維參數化設計空間ζ進行樣本采集,生成目標任務樣本集{zT,yT}n。另一方面,基于VAE編碼器,將以散點坐標表示的已完成任務樣本{xS,yS}m編碼至目標任務參數化設計空間,生成{zS,yS}m。上述過程又稱為已完成任務樣本重參數化,如圖7中虛線框所示。最后進一步耦合{zT,yT}n和{zS,yS}m,基于TGO算法流場開展型線設計空間尋優。

圖7 VAE-TGO方法設計優化框架Fig.7 VAE-TGO design optimization framework

采用NURBS和FFD等傳統參數化方法替代圖7中的VAE參數化方法,可構建基于傳統參數化方法的知識遷移優化框架,分別命名為NURBS-TGO和FFD-TGO法。但與VAE-TGO方法不同,NURBS-TGO和FFD-TGO方法難以將散點坐標表示的樣本重參數化至目標任務參數化設計空間,因而NURBS-TGO和FFD-TGO方法僅在目標任務與已完成任務樣本具有相同參數化設計空間的情形進行。

3 氣動型線遷移優化典型案例測試

本節以跨聲速翼型設計優化為例,對搭建的VAE-TGO方法的有效性進行驗證。

3.1 目標優化問題及遷移源任務描述

參照相關研究工作[8,27],選取最大化翼型升阻比CL/CD(CL為升力系數,CD為阻力系數)為目標任務的優化目標函數,選取優化工況為Ma=0.75,Re=6.5×105,迎角α=0°。為滿足結構強度要求,以RAE2822翼型作為參考設計,要求優化翼型截面積不小于參考面積的90%。對應的優化模型可表示為

(9)

式中:A(z)和ARAE2822分別為優化設計和參考設計的翼型截面積。

與此同時,用于知識遷移的已完成任務工況假定為Ma=0.45,Re=3.5×105,迎角α=0°。

3.2 優化過程相關設置

3.2.1 XFOIL性能評估求解器

選取廣泛使用的XFOIL求解器,對優化過程中生成的翼型進行氣動性能評估[28]。該軟件理論基礎為基于小擾動勢流理論的面源法,以位于邊界層位移厚度內流和外流的邊界條件為迭代收斂的標志。由于XFOIL求解器對小攻角條件下的翼型擾流問題計算精度較高,被廣泛應用于翼型設計優化性能的評估過程[8-9,29-30]。圖8展示了RAE2822翼型在工況條件為Ma=0.676、Re=5.7×105、迎角α=2.4°下,XFOIL求解器的數值計算結果與文獻 [28]中實驗結果的對比。由圖可見,XFOIL求解器得到的數值解與實驗結果吻合良好,可滿足優化設計過程中性能評估的精度要求。

圖8 XFOIL求解器計算結果與實驗結果[28]對比Fig.8 Comparison of results of XFOIL and experimental data

3.2.2 優化方法相關設置

為驗證知識遷移策略的有效性,分別采用知識遷移策略的優化方法與無知識遷移的傳統優化方法求解式(9)所示的目標任務。除VAE參數化方法外,NURBS和FFD等傳統方法亦被用于跨聲速翼型參數化建模。其中,采用已完成任務樣本進行知識遷移加速的優化過程被分別命名為VAE-TGO、NURBS-TGO和FFD-TGO方法,而不采用已完成任務樣本進行知識遷移的傳統優化過程則被命名為VAE-EGO、NURBS-EGO和FFD-EGO方法。

在進行翼型設計空間參數化建模時,VAE將以UIUC數據集作為訓練樣本集,VAE參數空間ζ的變量維度為10。NURBS和FFD參數化建模將以RAE2822翼型作為參考型線,參考陳偉等[8]相關工作完成NURBS與FFD方法的參數化空間設置。

注意到在已完成任務場景中,樣本{xS,yS}m的分布特征依根據算法尋優過程而定,無法事先設置且不能人為更改。為模擬上述已完成任務場景,在參數化建模的基礎上開展工況條件為Ma=0.45、Re=3.5×105、迎角α=0°的氣動型線優化設計,所生成對應的優化樣本將作為{xS,yS}m的候選樣本集。為模擬已完成任務樣本可能來自不同參數化空間的情形,從已完成任務優化解集中選取40個性能最優的個體{xS,yS}40,按照圖7所示流程,采用VAE編碼器對已完成任務樣本重參數化,在獲得目標參數空間樣本{zS,yS}40后開展遷移優化。

與VAE-TGO方法不同,由于NURBS和FFD方法難以將散點坐標表示的型線樣本編碼至目標任務參數化設計空間,因而在采用NURBS和FFD方法完遷移源任務優化后,直接從已完成任務優化解集中選取性能最優的40個樣本{zS,yS}40,用于NURBS-TGO和FFD-TGO方法的優化過程。

在EGO和TGO算法設置方面,相關參數設置與2.2.3節標準算例保持一致,即采用指數型高斯核函數分別構建單保真度和多保真度代理模型。同時,采用拉丁超立方抽樣技術生成40個目標任務的初始樣本,優化過程所允許的總樣本評估次數設為140。

3.3 結果分析

基于3.2節相關設置,采用VAE-TGO等不同優化方法,對獨立抽取的初采樣和遷移源樣本開展10次優化,得到的優化結果如圖9所示。由于采用拉丁超立方抽樣技術所生成的目標任務初始樣本的分布不同,因而10次優化所得到的最優解存在差異。圖9(a)和(b)分別展示了10次優化平均結果收斂過程和所得到的最優解分布。

(a)平均優化結果收斂曲線

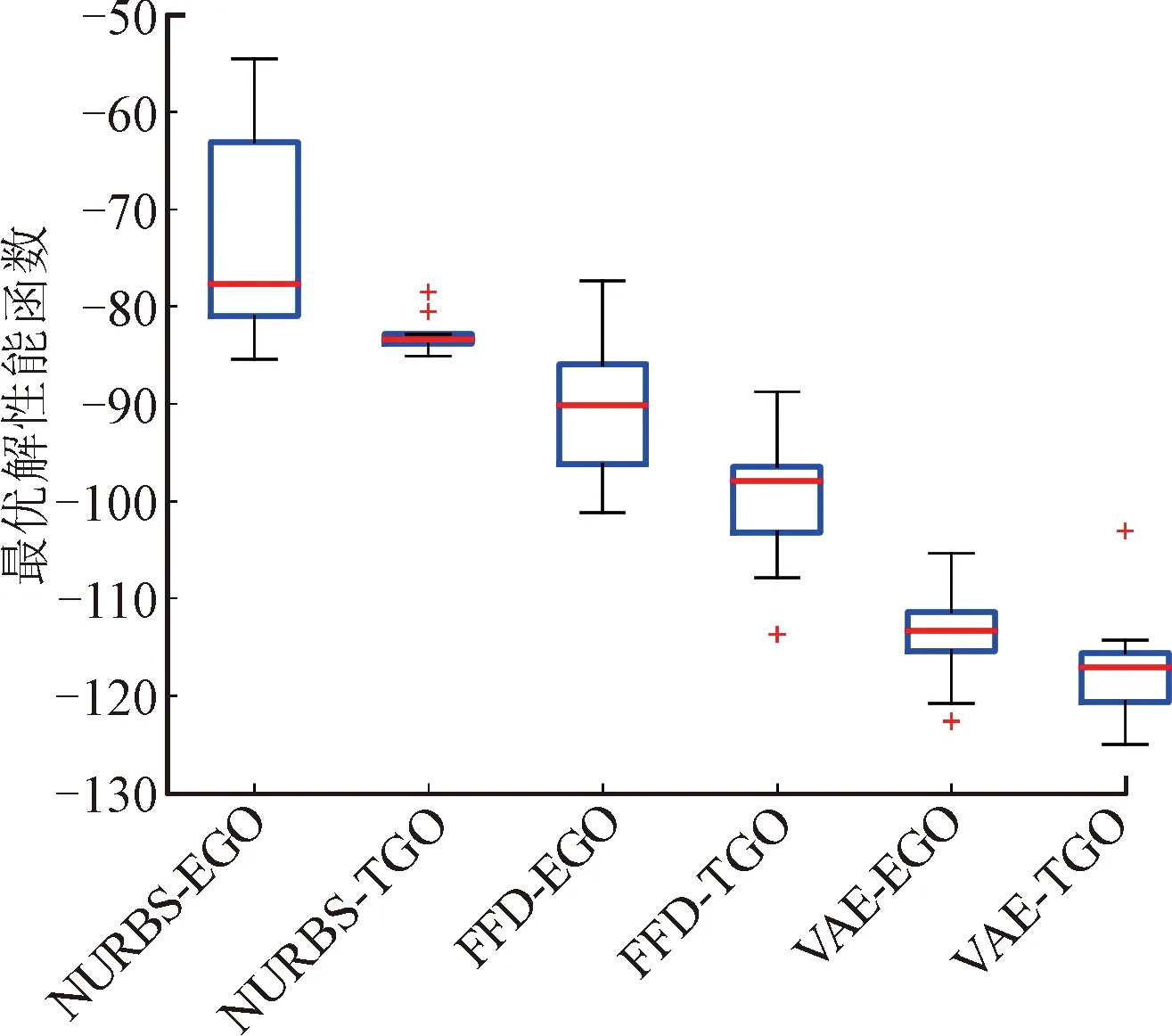
(b)最優解統計箱線圖

相較而言,采用VAE方法的翼型優化結果在優化收斂速度和最優解性能方面均顯著優于基于NURBS和FFD方法所得到的優化結果,這和李繼超等[1]、陳偉等[8]獲得的結果相類似。由于NURBS和FFD等傳統參數化方法需先選定參考型線,所構建的參數空間型線樣本形狀往往需要對參考翼型進行小幅度調整,因而參數空間內性能優異的型線樣本相對匱乏。相反地,基于VAE模型的參數化方法將囊括了從低速翼型到跨聲速翼型等各式各類型線的UIUC數據庫作為訓練數據,且VAE深度學習模型的非線性特征捕捉能力強,可較好地捕捉數據庫中各類翼型的幾何特征,因而使得VAE參數空間樣本多樣性強,且所囊括的性能優異的型線樣本更為豐富。因此,基于VAE方法的優化收斂曲線從初始階段開始,所得到的最優解即顯著優于FFD和NURBS方法的優化結果。

基于相同的參數化模型,將TGO方法的優化結果與無知識遷移的EGO方法的優化結果進行比較后可知,對于所采用的VAE、FFD、NURBS這3種參數化方法,TGO方法的優化過程在優化進程和取得最優解兩個方面均明顯優于無知識遷移的EGO方法的優化過程。由此表明,本文提出的多保真度遷移優化策略與多平臺遷移優化策略能有效提取已完成任務優化解集中有用的設計信息,從而顯著提高目標任務的求解速度與最優解性能。

在進一步探究采用知識遷移策略的有效性之前,以最優解集中的中位數作為代表,對采用不同優化方法所得到的最優型線進行氣動分析。圖10展示了RAE翼型和中位數解所對應的氣動型線。由圖可見,相較于RAE2822翼型,優化后的翼型彎曲程度明顯增加,靠近尾緣的區域曲線上凹趨勢最為明顯,此區域型線的變化有利于在吸力面增大氣流速度、降低當地靜壓,在壓力面降低氣流速度且提高當地靜壓,從而達到顯著提升翼型升力的目的。表4給出了不同設計方法得到的最優設計性能對比,可見相較于RAE2822翼型,優化后翼型的升力系數和升阻比均顯著增加,但優化翼型阻力系數卻略有增加,這與式(9)所選取的目標函數有關。在未來的優化研究中,加入關于阻力系數的約束條件有望解決上述不足。

(a)RAE2822

(b)NURBS-EGO

(c)FFD-EGO

(d)VAE-EGO

(e)NURBS-TGO

(f)FFD-TGO

(g)VAE-TGO

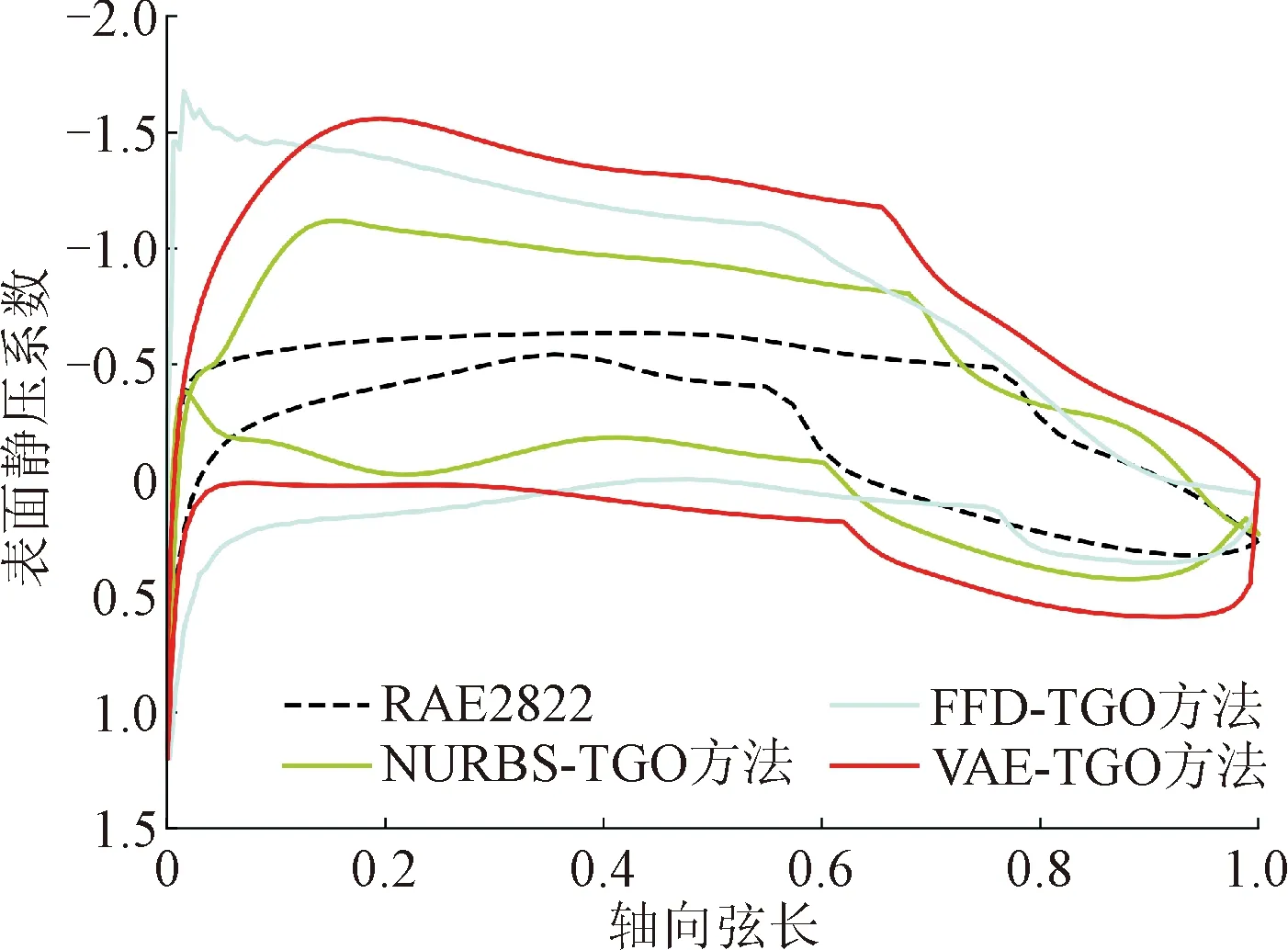
圖11進一步展示了不同翼型表面的壓力系數分布。由圖可見,相較于RAE2822翼型,優化后翼型的載荷明顯提升,這與表4中各優化解所對應的升力系數顯著提升的結果吻合較好。與此同時,從各優化翼型表面壓力系數分布易見,翼型表面流動組織良好,沒有出現大迎角和大分離的情況,表明優化后的翼型氣動性能良好。

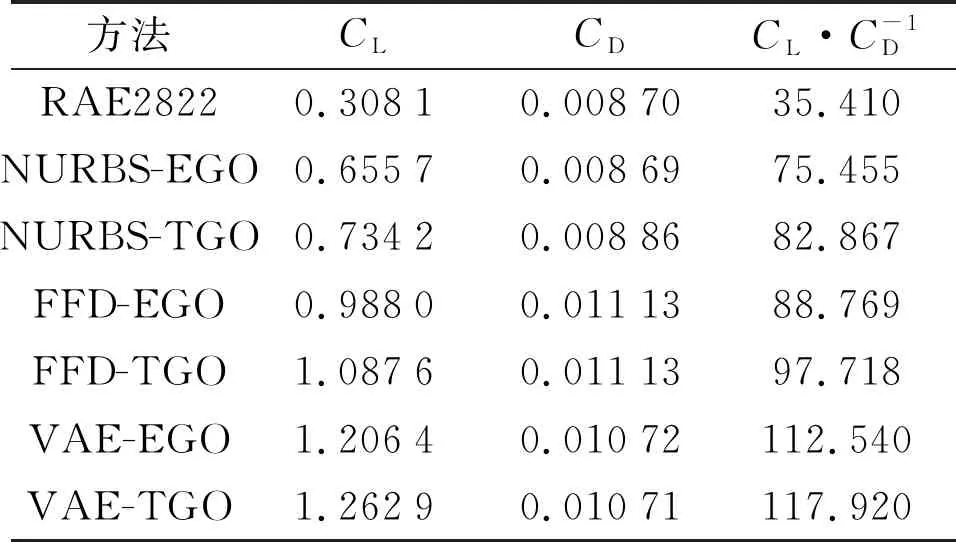
表4 不同設計方法得到的最優設計性能對比

(a)未使用知識遷移策略

(b)使用知識遷移策略

3.4 遷移優化機理討論

在驗證優化解性能有效性的基礎上,本節對知識遷移可加速目標任務優化進程的原因進行了探究。采用VAE參數化模型生成1 024個型線樣本,分別計算已完成任務工況和目標任務工況下同一翼型的升阻比,并對其進行相關性分析,得到的結果如圖12所示。由圖可見,皮爾遜相關系數為0.911 0,表明對于Ma=0.75的目標任務工況與Ma=0.4的已完成任務工況,翼型表面流動存在一定的相似性,這與描述亞聲速翼型流動相似性的普朗特-葛勞渥法則吻合較好[31],即在迎角不變的情況下,不同工況下翼型的表面靜壓系數分布可近似地按來流馬赫數的單值函數縮放。這一流動相似性法從理論上佐證了已完成任務與目標任務間的相關性。

圖12 同一翼型不同工況下的性能指標相關性Fig.12 Correlation between performances of identical airfoil under different working conditions

在驗證目標優化任務與已完成任務流動相似性的基礎上,對采用知識遷移可加速目標任務優化進程的機理可作如下解釋:一方面,在目標任務與已完成任務相似性較高的前提下,將已完成任務樣本與目標任務樣本耦合后構建多保真度代理模型,可有效提高用于捕捉設計空間全局趨勢的代理模型精度,進而加速目標任務的求解;另一方面,已完成任務與目標任務流動的相似性表明,已完成任務與目標任務的最優解分布在設計空間相同的鄰域。因此,將已完成任務樣本加入到目標任務建模與求解過程中,可幫助優化求解器更快地到達目標任務最優解鄰域,從而加速目標任務優化進程。

4 結 論

受機器學習領域遷移學習理念的啟發,將深度學習模型VAE和貝葉斯優化算法相結合,采用知識遷移加速研發了智能氣動形狀設計優化方法,主要獲得以下結論。

(1) 相對于NURBS、FFD等傳統參數化方法,采用VAE方法所構建的翼型參數化設計空間樣本的多樣性更強,表明基于VAE方法的優化設計結果顯著優于基于傳統參數化方法所獲得的優化解。此外,VAE編碼器結構可將采用不同參數化方法建模的已完成任務樣本編碼至相同的參數化設計空間,為拓展遷移優化方法在氣動形狀設計領域的應用提供契機。

(2) 數值算例與翼型氣動型線優化的分析結果表明,將多保真度建模的序列遷移策略與多平臺遷移優化策略相結合,可充分挖掘已完成任務樣本中所包含的有用設計信息,從而顯著加速目標任務優化進程,得到的最優解性能明顯優于無知識遷移的傳統優化方法優化解。

為驗證知識遷移策略的有效性,本文主要針對翼型的氣動性能展開優化設計,但該方法可通用于考慮結構強度約束的翼型多學科設計優化問題,并可推廣至航空發動機葉片二維及三維多學科設計優化。