反應擴散系統中交叉擴散引發的圖靈斑圖之間的轉變*

孟星柔 劉若琪 賀亞峰 鄧騰坤 劉富成

(河北大學物理科學與技術學院,保定 071002)

1 引言

圖靈斑圖是均勻定態經歷圖靈失穩而自發產生的空間定態圖紋,其廣泛存在于生物體、生態系統、地球化學以及物理化學等領域[1-4].圖靈失穩的機理是擴散所引起的不穩定性[5],因此,擴散是反應擴散系統圖靈斑圖形成的關鍵因素.以前的研究大都只考慮自擴散過程[6-9],但在實際系統中,給定物種的擴散通量也會受到其他物種梯度的影響[10],即存在交叉擴散.例如,社會系統中的人口統計學[11],生態系統中的物種遷移[12],物理系統中的靜電相互作用和排除體積效應[13],化學系統中的化學波動力學[14]以及粒子運輸過程[15]等都會導致交叉擴散效應.

自Kerner[16]首次提出交叉擴散以來,人們逐漸認識到自擴散與交叉擴散的相互作用可以使反應擴散系統產生更為豐富的時空斑圖動力學[17-19].在自擴散作用下,圖靈不穩定性只能由長程抑制和短程激活來觸發,但引入交叉擴散項解除了這種限制[11].交叉擴散可以影響反應擴散系統中圖靈不穩定性的形成與消失[20-22].Chung 和Peacock-López[23]在帶有交叉擴散項的自我復制化學模型中,分析獲得了表征龐加萊-阿德羅諾夫-霍普夫分岔和圖靈分岔參數之間的精確關系.此外通過改變交叉擴散系數,可以實現六邊形與條紋斑圖之間的轉變[11,24,25].上述關于交叉擴散的研究中只針對雙向交叉擴散,盡管從理論結果上雙向擴散包含了單向擴散,但在實際的復雜系統,尤其是生命系統以及生態系統中,單向交叉擴散更加符合實際情況.例如,由于食物鏈的單向性,病毒傳播過程中健康人類對患病禽類并沒有影響[26];由于季節變化、覓食以及繁殖等因素引起動物的周期性遷移[27].但是鮮有研究者單獨考慮單向交叉擴散的影響,且其單獨作用機理尚不清楚.交叉擴散的方向性對斑圖動力學的影響尚需進一步研究[28,29].

復雜系統中物質的擴散過程一般來說與物質濃度密切相關,因此常擴散系數的反應擴散模型無法精確描述復雜系統[30-32].研究發現濃度依賴的擴散系數對斑圖形成和選擇以及轉變有著很大的影響.Zemskov 等[33]理論分析了濃度依賴交叉擴散作用下圖靈不穩定性的條件.Li 等[34,35]研究了自擴散系統中受局域濃度調控下圖靈斑圖的形成機制,發現控制調控系數可實現六角斑圖和條紋斑圖共存并且可以調節二者比例.通過在圖靈系統中施加一個圓偏振電場,也可實現六邊形與條紋斑圖之間的轉化[36,37].在可激發的介質中,濃度依賴性擴散可實現自我復制行為到穩定空間結構的轉變[38].Gambino 等[39]發現在沒有霍普夫和波不穩定性的反應擴散系統中,引入交叉擴散項可以產生閃爍六邊形和其他振蕩圖靈斑圖.Mukherjee 等[40]發現在濃度依賴交叉擴散項的影響下,自擴散模型中的混沌動力學可以被抑制,從而達到穩態或保持穩態.從擴散本質上來講,交叉擴散來源于物質之間的相互作用,因此一種物質的交叉擴散系數,除了與自身濃度相關外,還應當與其他物質的濃度有關,例如生態系統中的植被動力學,水的濃度可以誘導植被格局的轉變,促進植被的密度,可預警荒漠化[41].到目前為止,大多數線性依賴濃度的交叉擴散的研究集中于依賴自身濃度,但是還缺乏對交叉擴散依賴另一變量濃度的研究.針對上述情況,本文通過在反應擴散系統中引入不同形式的交叉擴散項,系統研究了交叉擴散的方向性以及濃度依賴性在圖靈斑圖轉變過程中的作用.

2 物理模型

布魯塞爾(Brusselator)模型是一種典型的反應擴散模型,因其理論分析與實驗結果定性吻合,被廣泛用于研究圖靈斑圖動力學[42].將交叉擴散引入到該模型中,在無量綱的情況下,其形式如下:

其中u和v分別為活 化子與阻滯子濃度;a和b均為系統動力學參數;Du和Dv分別為物質u,v的自擴散系數.本文固定參數a=3,b=9,Du=3,以及Dv=10,以確保在無交叉擴散情況下系統未經歷霍普夫分岔,而經歷圖靈分岔,從而確保圖靈斑圖的產生.Duv和Dvu為活化子與阻滯子之間的交叉擴散系數,其值可正可負,且在通常情況下依賴于兩種物質的濃度[43].

對系統的均勻定態解 (u0,v0)=(a,b/a) 進行線性穩定性分析,得到線性本征方程:

其中J為雅可比矩陣,D為擴散系數矩陣:

對線性本征方程進行求解可以得到本征值λ,進而可以分析系統的分岔類型.在交叉擴散為常數的情況下,圖靈分岔滿足的條件為[10]

由這些不等式共同決定的區域就是圖靈斑圖所能形成的參數區域,即圖靈空間.

圖1 給出了Duv-Dvu平面內的圖靈空間分布情況.圖中每條曲線都對應著不等式所確定區域的邊界.不等式(3a)所確定的區域以DuvDvu的乘積為邊界,如圖1 中點線所示.當乘積DuDv為正值時,該區域在第一和第三象限的兩個雙曲線內.不等式(3b)所確定的區域也以D uvD vu的乘積為邊界,且其數值應當大于某一負值,因此該區域位于第二和第四象限的雙曲線內.不等式(3c)對應著一條直線,將平面分為兩個區域,圖靈區域位于直線下方.最后,不等式(3d)得到一個橢圓,圖靈區域在橢圓區域之外.

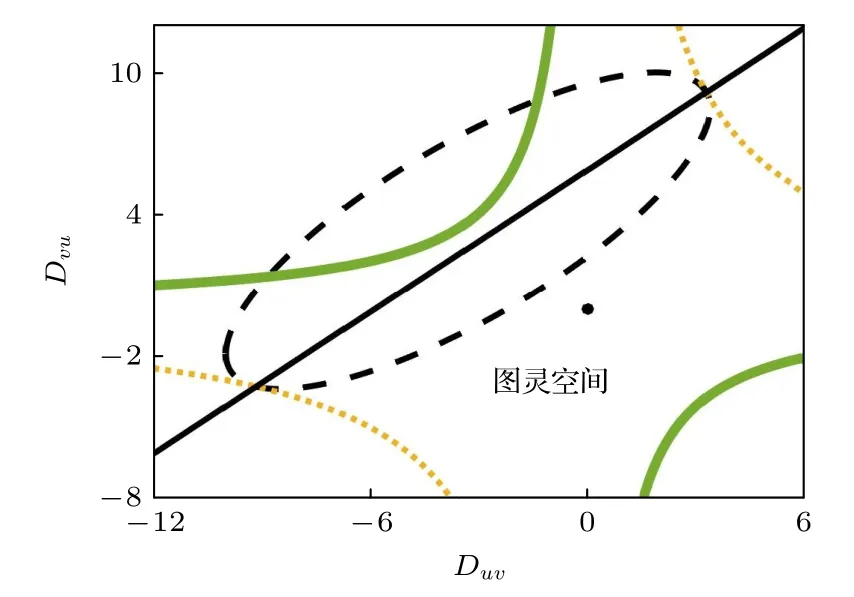
圖1 a=3,b=9,D u=3,D v=10 時,交叉擴散存在下的圖靈空間.點線、粗實線、細實線和虛線分別對應(3a)式—(3d)式Fig.1.Turing space in the present of cross diffusion for a=3,b=9,D u=3,and D v=10.Thick solid line,dotted line,thin solid line,and dotted line correspond to Eqs.(3a)-(3d),respectively.

線性穩定性分析只能得到圖靈斑圖的存在空間,但無法確定圖靈斑圖的類型.為此本文利用多重尺度的方法推導出系統經歷圖靈分岔后二維圖靈斑圖的振幅方程,并據此分析圖靈斑圖的選擇問題[44,45].由于篇幅限制,這里只給出主要結果.

為方便本文仍然使用原變量,系統方程(1)在平衡點 (u0,v0) 處的泰勒展開式為

在臨界點附近,方程解的形式可寫為

方程(4)可寫為如下形式:

式中L為線性算符,N為非線性算符,它們分別為

選取b為控制參數,bT為對應的臨界值.將控制參量b、變量c與非線性項N按小量ε展開:

其中,

線性算符L可分解為

其中,

利用中心流理論[44]推導可得如下振幅方程:

其中,μ表示臨界值的歸一化距離;τ0表示弛豫時間.計算可得方程中系數μ,τ0,h,g1,g2的表達式分別為

當系統偏離分岔點,需要考慮μ的影響,將系數h修正為[45]

其中,p滿足,q滿足為LT的伴隨算子.G1,G2和H的表達式可參見文獻[46].

振幅方程(5)中的每個解都對應著一種斑圖類型.振幅系數Aj可分解為模ρj=|Aj|及一個相應的相角?j,將Aj=ρjexp(i?i) 代入振幅方程并分離實部和虛部,可得如下方程:

其中,?=?1+?2+?3,上述系統有下列4 種類型的解,分別對應均勻定態、條紋斑圖、六邊形斑圖以及混合態斑圖.

1)定態解(0):

當μ＜μ2=0 時,定態解穩定,當μ＞μ2時,定態解不穩定.

2)條狀斑圖(S):

根據μ=h(μ)2g1/(g2-g1)2可得到兩個解.當＜時,條紋斑圖穩定.

3)六邊形斑圖(H0,Hπ) :

六邊形斑圖的類型由振幅方程中的二次項系數h決定.當h ＞0 時,六邊形斑圖為H0(?=0),即點狀斑圖;當h ＜0 時,六邊形斑圖為Hπ(?=π),即蜂窩狀斑圖.六邊形斑圖解只有在μ＞μ1=時才存在.

當g2＞g1,μ＞時,該解存在.

方程(1)通過商業有限元計算軟件Comsol Multiphysics 進行數值求解.計算采用MUMPS 求解器,使用向后差分法進行時間離散,時間步長采用自適應步長,用10-4的相對精度進行控制.模擬區域大小為64×64,使用自由三角形網格進行空間離散,網格最大單元格大小0.64,最大單元增長率1.1.在均勻定態的基礎上附加一個10%的隨機擾動作為初始條件,邊界處選取無通量邊界條件.系統演化時間采用104無量綱時間,系統在演化時間5000 左右后趨于穩定.

3 模擬結果與討論

為了系統研究交叉擴散項對圖靈斑圖轉變的影響,分別討論了交叉擴散系數為常數以及線性依賴濃度時的兩種情況.在常數交叉擴散系數情況下,從單向交叉擴散以及雙向交叉擴散兩個角度分析了交叉擴散方向性的作用.

圖2 給出了交叉擴散項Dvu=0,Duv≠0 時,阻滯子向活化子的交叉擴散對圖靈斑圖的影響.其中圖2(a)為不同交叉擴散系數Duv下的色散關系曲線,曲線為特征值的實部 Re(λ),代表了圖靈模的線性增長率,Re(λ) 越大,圖靈模式增長越快.隨著擴散系數Duv的增大,臨界值的歸一化距離μ不斷增大,圖靈模波數及其對應的 Re(λ) 逐漸增大,系統逐漸遠離初級分岔點.偏離分岔點的程度是模式選擇過程中的一個重要因素.隨著系統偏離圖靈分岔點的程度逐漸增大,系統經歷均勻態→蜂窩六邊形→條紋→點狀六邊形的轉變[42,45,47],定義上述轉變次序為正向轉變,反之則為反向轉變.圖2(b)—(d)給出了交叉擴散項Duv作用下條紋斑圖向點狀六邊形斑圖轉變的過程.當交叉擴散項Duv=0 時,即自擴散情況下,此時μ滿足=0.2882,系統產生圖2(b)所示的條紋斑圖.在單向交叉擴散項Duv的作用下,系統逐漸遠離圖靈分岔點,Duv=2 時,μ滿足=0.5434＜μ=0.5459=1.2678,系統處于條紋與點狀六邊形同時存在的雙穩區域,因此系統表現出條紋與點狀六邊形混合斑圖(圖2(c)),由于μ更接近,因此條紋斑圖優于點狀六邊形斑圖.當Duv=4.5 時,臨界值的歸一化距離μ繼續增大,此時μ滿足=0.8679,且靠近,系統轉變為圖2(d)所示的點狀六邊形斑圖.圖2 結果表明,阻滯子向活化子的交叉擴散會導致系統逐漸遠離初級分岔點,從而引發圖靈斑圖的正向轉變,且數值模擬結果與理論分析相符.

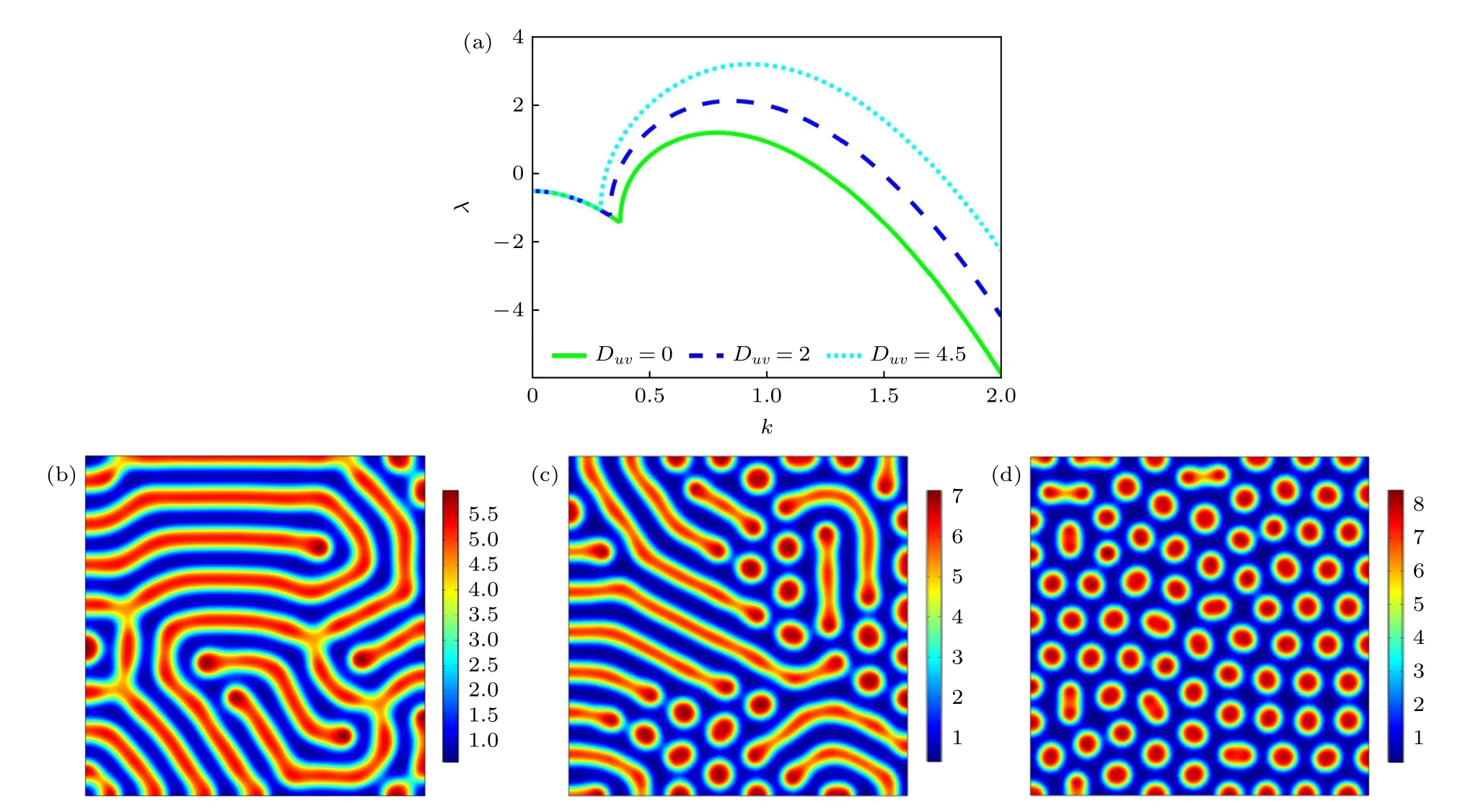
圖2 單向交叉擴散 Duv 引發的圖靈斑圖轉變 (a)色散曲線;(b)條紋斑圖,Duv=0 ;(c)點狀六邊形與條紋混合斑圖,Duv=2 ;(d)點狀六邊形斑圖,Duv=4.5Fig.2.Turing pattern transition induced by one-way cross diffusion term Duv : (a) Dispersion curves;(b) stripe pattern,Duv=0 ;(c) mixed pattern with stripes and spots,Duv=2 ;(d) hexagonal spot pattern,Duv=4.5.

圖3 研究了交叉擴散項Duv=0,Dvu≠0 時,活化子向阻滯子的交叉擴散對圖靈斑圖轉變的影響.圖3(a)為不同交叉擴散系數Dvu下的色散關系曲線,隨著擴散系數Dvu的增大,臨界值的歸一化距離μ不斷減小,圖靈模波數及其對應的Re(λ)逐漸減小,系統逐漸靠近圖靈分岔點并最終低于圖靈分岔點.圖3(b)—(d)為在單向交叉擴散系數Dvu作用下,系統從條紋經歷蜂窩六邊形最終穩定成均勻態的轉變過程.相較于自擴散的情況,當交叉擴散系數Dvu=0.5 時,系統相對靠近圖靈岔點,μ略微減小,但仍滿足＜μ=0.2103,因此系統表現為圖3(b)所示的條紋斑圖.隨著Dvu增大到1.5,此時μ滿足=0.0665＜μ=0.0796=0.1871,系統處于蜂窩狀六邊形與條紋同時存在的雙穩區域,但由于μ更接近,因此系統表現出圖3(c)所示的蜂窩狀六邊形斑圖.當Dvu=3時,由于超出了圖1 中圖靈空間的參數范圍,此時特征值的實部 Re(λ) 低于圖靈分岔點,系統逐漸穩定成均勻態(圖3(d)).圖3 結果表明,活化子向阻滯子的交叉擴散會導致系統逐漸靠近初級分岔點,從而引發圖靈斑圖的反向轉變,且數值模擬結果與理論分析相符.

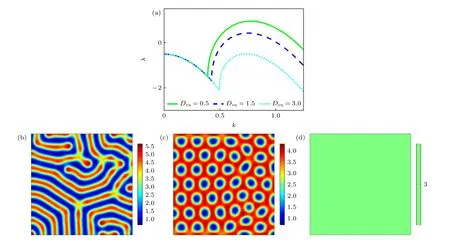
圖3 單向交叉擴散 Dvu 引發的圖靈斑圖轉變 (a)色散曲線;(b)條紋斑圖,Dvu=0.5 ;(c)蜂窩狀六邊形斑圖,Dvu=1.5 ;(d)均勻態,Dvu=3Fig.3.Turing pattern transition induced by one-way cross diffusion term Dvu : (a) Dispersion curves;(b) stripe pattern,Dvu=0.5 ;(c) honeycomb hexagonal pattern,Dvu=1.5 ;(d) uniform state,Dvu=3.

圖4 為對稱雙向交叉擴散(Duv=Dvu)對圖靈斑圖的影響,改變對稱交叉擴散系數會影響圖靈斑圖的參數區域,導致其發生轉變.其中圖4(a)為不同雙向交叉擴散系數下的色散曲線,隨著雙向交叉擴散系數的增大,系統逐漸遠離圖靈分岔點.當雙向交叉擴散系數Duv=Dvu=1 時,活化子與阻滯子之間的交叉擴散效應較小,此時系統偏離圖靈分岔點的程度與自擴散時系統偏離圖靈分岔點的程度相當,μ滿足＜μ=0.2642,因此系統仍然表現為條紋斑圖,如圖4(b)所示,在對稱雙向交叉擴散情況下數值模擬結果也與理論分析相符.隨著對稱雙向交叉擴散系數的增大,μ逐漸增大,此時g ＜0,系統發生次臨界分岔,在次臨界區域,通過弱非線性分析得到三次Stuart-Landau規范性振幅方程不再適用,須將弱非線性展開式提高至五次,暫不予研究.但從色散關系曲線可知,此時系統相對遠離初級圖靈分岔點,因此產生如圖4(c)所示的蜂窩狀六邊形與條紋混合斑圖.當對稱雙向交叉擴散系數增大到5 時,此時失穩圖靈模式的區域增大,最危險圖靈模式增強,且其波數增大,因此系統表現為多模混合斑圖如圖4(d)所示.另外,當交叉擴散系數Dvu=0 時,增大擴散系數Duv,μ滿足,系統將會一直呈現出點狀六邊形斑圖,數值模擬結果以及理論分析均表明:在單向交叉擴散情況下,當阻滯子向活化子的交叉擴散效果足夠強時,不會出現多模混合斑圖.圖4結果表明,在對稱雙向交叉擴散作用下,阻滯子向活化子的交叉擴散效應要強于活化子向阻滯子的交叉擴散.

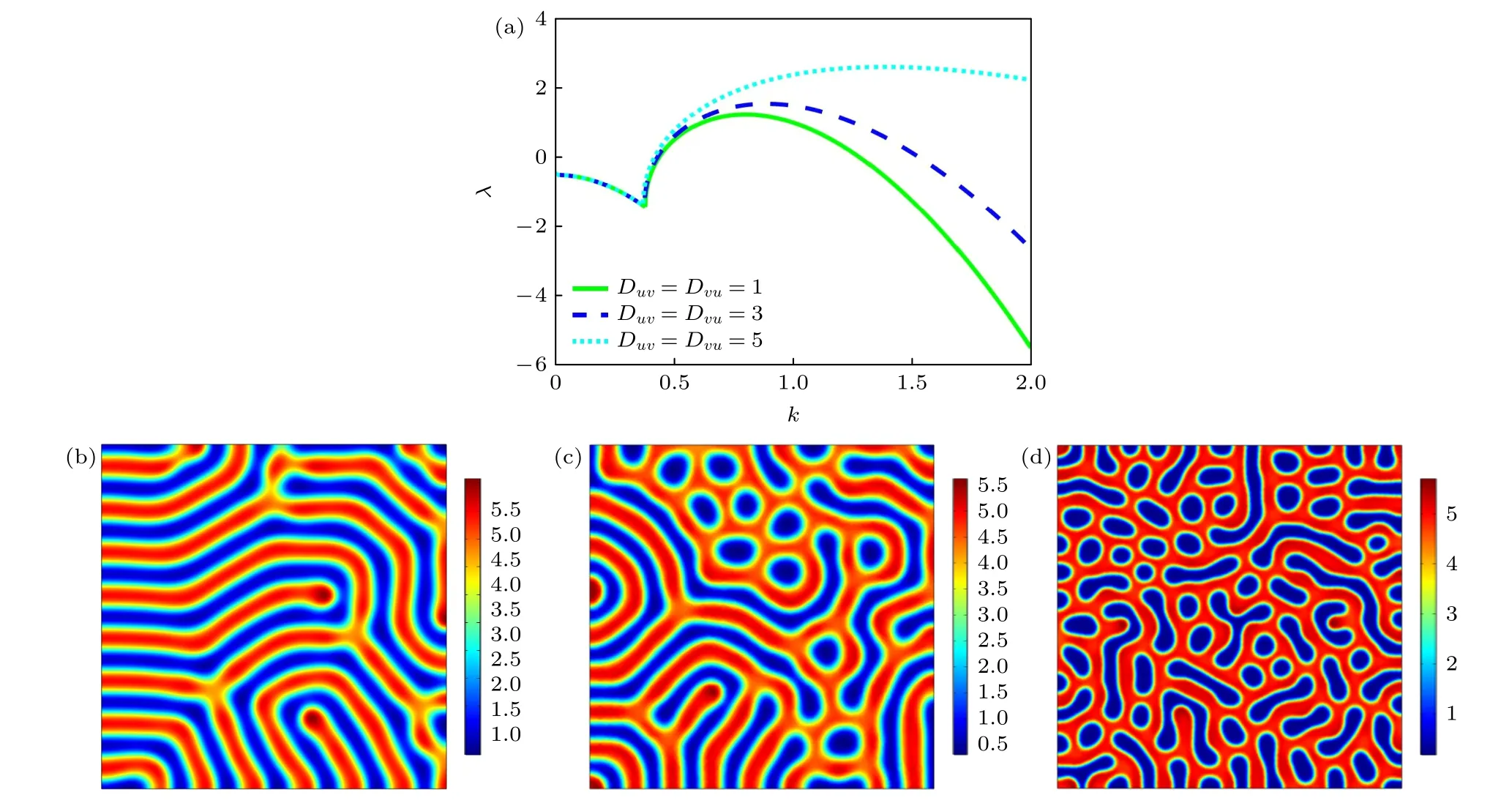
圖4 對稱雙向交叉擴散作用下圖靈斑圖的轉變過程 (a)色散曲線;(b)條紋斑圖,Duv=Dvu=1 ;(c)蜂窩狀六邊形與條狀混合斑圖,Duv=Dvu=3 ;(d)多模混合斑圖,Duv=Dvu=5Fig.4.Turing pattern transition induced by symmetrical two-way cross-diffusion: (a) Dispersion curves;(b) stripe pattern,Duv=Dvu=1 ;(c) mixed pattern with honeycomb hexagons and stripes,Duv=Dvu=3 ;(d) multimode mixed pattern,Duv=Dvu=5.

圖5 給出了非對稱雙向交叉擴散(Duv≠Dvu)對圖靈斑圖轉變的影響.圖5(a)為非對稱雙向交叉擴散作用下的色散曲線,固定Duv=1,逐漸增大Dvu,當交叉擴散系數Dvu ≈1.1 時,與系統自擴散下的色散曲線基本一致,當Dvu＞ 1.1 時,系統逐漸靠近圖靈分岔點并最終低于圖靈分岔點.圖5(b)—(d)給出了非對稱雙向交叉擴散下,斑圖從條紋經歷蜂窩狀六邊形向均勻態方向轉變的過程.當Dvu=0 時,μ滿足＜μ=0.4171,此時只有阻滯子向活化子的交叉擴散作用在系統上,會導致系統相對遠離初級分岔點,產生條紋斑圖如圖5(b).但當Dvu=2.5 時,活化子向阻滯子的交叉擴散效應要強于阻滯子向活化子的交叉擴散,因此系統相對靠近初級分岔點,呈現出如圖5(c)所示的蜂窩狀六邊形斑圖.當交叉擴散系數Dvu增大到5 時,特征值的實部 Re(λ) 低于圖靈分岔點,最終得到均勻態如圖5(d).圖5 結果表明,在非對稱雙向交叉擴散作用下,圖靈斑圖的轉變方向與交叉擴散系數的強度相關,若阻滯子向活化子的交叉擴散效應較強,則系統遠離圖靈分岔點發生正向轉變,與之相反,則系統靠近圖靈分岔點發生反向轉變.

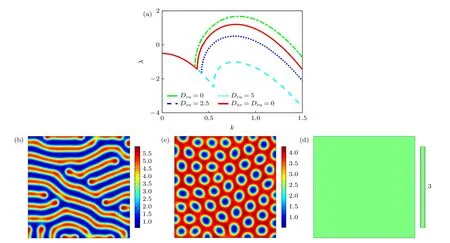
圖5 非對稱交叉擴散項下圖靈斑圖的轉變過程,Duv=1 (a)色散曲線;(b)條紋斑圖,Dvu=0 ;(c)蜂窩狀六邊形斑圖,Dvu=2.5 ;(d)均勻態,Dvu=5Fig.5.Turing pattern transition induced by asymmetrical two-way cross-diffusion at Duv=1 : (a) Dispersion curves;(b) stripe pattern,Dvu=0 ;(c) honeycomb hexagonal pattern,Dvu=2.5 ;(d) uniform state,Dvu=5.

在生物系統中,化學物質通過細胞運輸時受到局域化學物質濃度的影響[38].物質的擴散不僅依賴于自身的濃度,而且還依賴于其他物質的濃度,例如物種遷移,植被格局,多孔介質中的傳質過程等[21].因此引入線性依賴濃度的交叉擴散系數Dij=(1+βj)D0,進一步研究依賴其他變量的擴散系數對系統斑圖形成以及斑圖選擇的影響.其中i代表活化子u或阻滯 子v的濃度,j代表兩者中另一變量的濃度,β是濃度依賴的調節參數,而D0為恒定的擴散系數.本文從兩個角度分別進行研究: 1)活化子的交叉擴散系數Duv線性依賴于阻滯子濃度;2)阻滯子的交叉擴散系數Dvu線性依賴于活化子濃度.

圖6 為交叉擴散系數Dvu=2,Duv取不同調節參數β時斑圖的轉變過程.當β ＜-0.48 時,系統低于圖靈分岔點,因此當β=-0.6 時,呈現出均勻態,如圖6(a)所示.當-0.48＜β ＜-0.31 時,隨著參數β的增大,圖靈模本征值增大,系統高于圖靈分岔點,當β=-0.4 時,μ滿足μ1＜μ=-0.0215＜μ2,因此系統表現為蜂窩狀六邊形(圖6(b)).繼續增大β,g ＜0,系統發生次臨界分岔,三階的振幅方程不再適用.當-0.31＜β ＜-0.15 時,系統呈現出圖6(c)所示的蜂窩狀六邊形與條紋混合斑圖.當β ＞-0.15 時,系統與自擴散時偏離初級分岔點的程度相當,因此表現為條紋斑圖如圖6(d).當0.5＜β ＜1.4時,系統遠離圖靈分岔點,呈現圖6(e)所示的點狀六邊形與條紋混合斑圖,隨著調節參數的增大,點狀六邊形的比例逐漸增大.當β ＞1.4時,阻滯子向活化子的交叉擴散效應遠強于活化子向阻滯子的交叉擴散,系統表現為圖6(f)所示的點狀六邊形斑圖,并且隨著β的增大,點狀六邊形的波長減小.圖6 結果表明,當活化子的交叉擴散系數Duv線性依賴阻滯子濃度v時,隨著β的增大,系統逐漸遠離圖靈分岔點,從而引發圖靈斑圖的正向轉變.

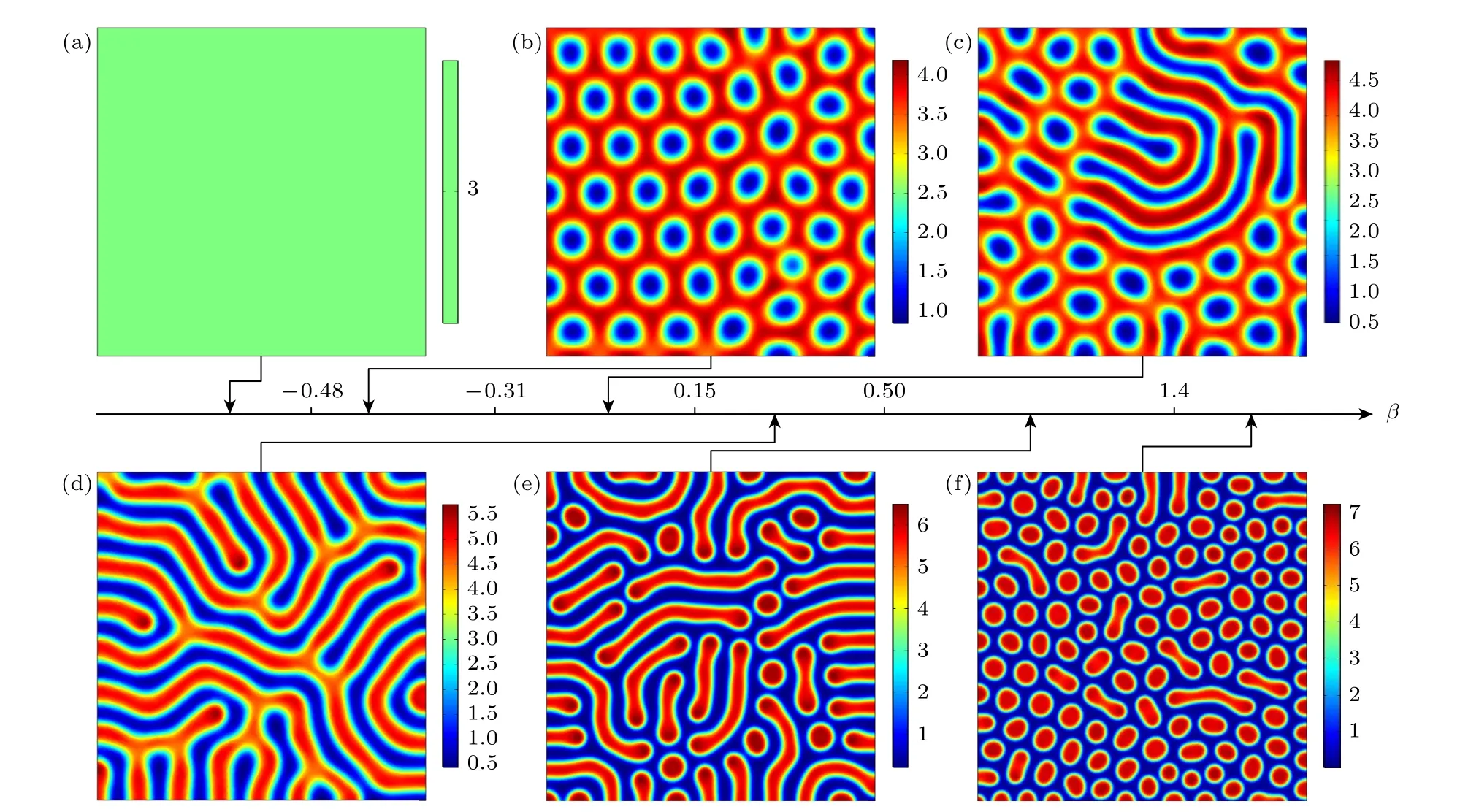
圖6 濃度依賴交叉擴散 Duv=D0(1+βv) 引起圖靈斑圖的轉變,D0=2,Dvu=2 (a) 均勻態,β=-0.6 ;(b) 蜂窩六邊形斑圖,β=-0.4 ;(c) 蜂窩六邊形與條紋混合斑圖,β=-0.2 ;(d) 條紋斑圖,β=0 ;(e) 條紋與點狀混合斑圖,β=0.8 ;(f) 點狀六邊形斑圖,β=1.5Fig.6.Turing pattern transition induced by cross-diffusion coefficient with concentration-dependence (Duv=D0(1+βv)),D0=2,Dvu=2 : (a) Uniform state,β=-0.6 ;(b) honeycomb hexagonal pattern,β=-0.4 ;(c) mixed pattern with honeycomb hexagons and stripes,β=-0.2 ;(d) stripe pattern,β=0 ;(e) mixed pattern with stripes and spots,β=0.8 ;(f) hexagonal spot pattern,β=1.5.

圖7 為交叉擴散系數Duv=2,Dvu取不同調節參數β時引起圖靈斑圖轉變的過程.當β ＜-0.25時,系統偏離初級分岔點最遠,圖7(a)為β=-0.3時,此時系統表現為點狀六邊形斑圖.當-0.25＜β ＜-0.2時,此時系統處于六邊形向條紋的過渡區,因此呈現出點狀六邊形與條紋混合斑圖,如圖7(b)所示.隨著β的增大,系統相對靠近圖靈分岔點,當β ＞-0.2 時,交叉擴散項Dvu與Duv對系統的作用相當,因此表現為自擴散時的斑圖類型,即圖7(c)所示的條紋斑圖.當 0.05＜β ＜0.1 時,此時系統處于條紋向六邊形的過渡區,因此呈現出蜂窩狀六邊形與條紋混合斑圖,如圖7(d)所示.當 0.1＜β ＜0.6 時,系統繼續靠近初級分岔點呈現出圖7(e)所示的蜂窩狀六邊形.當β ＞0.6 時,活化子向阻滯子的交叉擴散作用使系統低于圖靈分岔點,因此系統穩定成如圖7(f)所示的均勻態.圖7結果表明,當阻滯子的交叉擴散系數Dvu線性依賴活化子濃度u時,隨著β的增大,系統逐漸靠近并最終低于圖靈分岔點,從而引發圖靈斑圖的反向轉變.濃度依賴性交叉擴散會影響圖靈斑圖的轉變方向,因此,研究濃度依賴性交叉擴散可預防荒漠化,對物種生存與滅絕等問題具有重要指導意義.另外,本文進一步研究了交叉擴散系數依賴自身變量以及同時依賴兩個變量的情況,結果表明相較于交叉擴散系數依賴另一個變量的情況,依賴自身變量時僅增大了圖靈斑圖的參數范圍,而同時依賴兩個變量時僅減小圖靈斑圖的參數范圍,對斑圖其他性質沒有明顯影響.

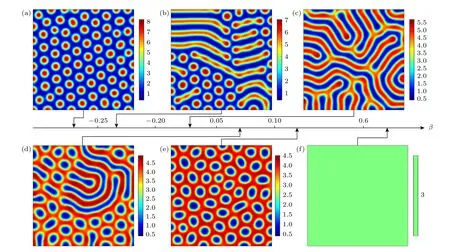
圖7 濃度依賴交叉擴散 Dvu=D0(1+βu) 引起圖靈斑圖的轉變,D0=2,Duv=2 (a) 點狀六邊形斑圖,β=-0.30 ;(b) 條紋與點狀六邊形混合斑圖,β=-0.22 ;(c) 條紋斑圖,β=0 ;(d) 蜂窩狀六邊形與條紋混合斑圖,β=0.08 ;(e) 蜂窩狀六邊形斑圖,β=0.20 ;(f) 均勻態,β=0.80Fig.7.Turing pattern transition induced by cross-diffusion coefficient with concentration-dependence (Dvu=D0(1+βu)),D0=2,Duv=2 : (a) Hexagonal spot pattern,β=-0.30 ;(b) mixed pattern with stripes and spots,β=-0.22 ;(c) stripe pattern,β=0 ;(d) mixed pattern with honeycomb hexagons and stripes,β=0.08 ;(e) honeycomb hexagonal pattern,β=0.20 ;(f) uniform state,β=0.80.

4 結論

本文通過在布魯塞爾反應擴散系統中引入不同形式的交叉擴散系數,系統研究了交叉擴散的方向性以及濃度依賴性對圖靈斑圖演化過程的影響.在圖靈分岔點附近進行弱非線性穩定性分析,得到了系統的振幅方程,給出了不同類型斑圖的存在條件,并利用數值模擬對理論分析進行了驗證,模擬結果與理論一致.結果表明,單向交叉擴散即可引起圖靈斑圖的轉變,且交叉擴散的方向直接決定了斑圖轉變的次序.隨著阻滯子向活化子交叉擴散強度的增大,系統會逐漸遠離初級分岔點,從而引發圖靈斑圖向點狀六邊形斑圖的正向轉變.反之,隨著活化子向阻滯子交叉擴散強度的增大,系統會逐漸靠近圖靈分岔點,引發圖靈斑圖向均勻態的反向轉變.對稱雙向交叉擴散作用下,隨著交叉擴散系數的增大系統發生反向轉變,表明阻滯子向活化子的交叉擴散效應要強于活化子向阻滯子的交叉擴散.非對稱雙向交叉擴散作用下,圖靈斑圖的轉變方向與交叉擴散系數的強度相關,若阻滯子向活化子的交叉擴散效應較強則系統遠離圖靈分岔點發生正向轉變,與之相反,則系統靠近圖靈分岔點發生反向轉變.當活化子的交叉擴散系數Duv線性依賴阻滯子濃度v時,隨著調節參數β的增大,引發圖靈斑圖正向轉變;相反,當阻滯子的交叉擴散系數Dvu線性依賴活化子濃度u時,引發圖靈斑圖的反向轉變.以上研究結果揭示了交叉擴散的方向性和濃度依賴性影響圖靈斑圖轉變方向的機制,對研究交叉擴散對復雜非線性系統中植被格局、粒子運輸、材料生長等其他斑圖的產生機制及類型選擇具有重要借鑒意義.