關于2023年北京高考物理第16題(4)問不同解法的探討
鄧 飛 高荷潔(特級教師)
(北京工業大學附屬中學)
2023年北京高考物理第16題對平拋運動實驗進行了考查,其中第(4)問更是側重于對實驗分析等綜合能力的考查.該問涉及的物理情境雖然是大家熟知的利用“頻閃照相”記錄小球的位置,主要方法是利用運動的合成與分解,來分析解決實驗中遇到的實際問題,但是設問方式卻較以往有很大變化,對考生的科學思維能力要求較高.下面我們一起來探討一下這道題的三種不同解法.
題目某同學實驗時忘了標記重垂線方向,為解決此問題,他在頻閃照片中,以某位置為坐標原點,沿任意兩個相互垂直的方向作為x軸和y軸正方向,建立直角坐標系xOy,并測量出另外兩個位置的坐標值(x1,y1)、(x2,y2),如 圖1 所示.根據平拋運動規律,利用運動的合成與分解的方法,可得重垂線方向與y軸間夾角的正切值為_________.
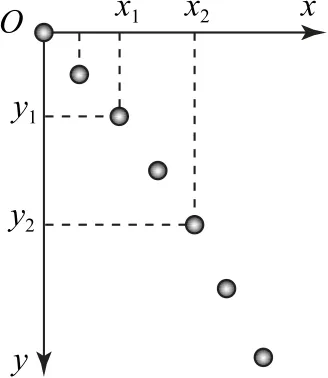
圖1
分析沿實際的水平方向和豎直方向作x′軸和y′軸,建立直角坐標系x′Oy′,可能的情況有兩種:y相對于y′向左偏和y相對于y′向右偏.下面我們分情況討論.
情況1y相對于y′向左偏,如圖2所示,設y與y′的夾角為θ,將水平方向的初速度v0、豎直方向的速度vy和重力加速度g沿x和y軸分解,g分解后有gx=gsinθ,gy=gcosθ.
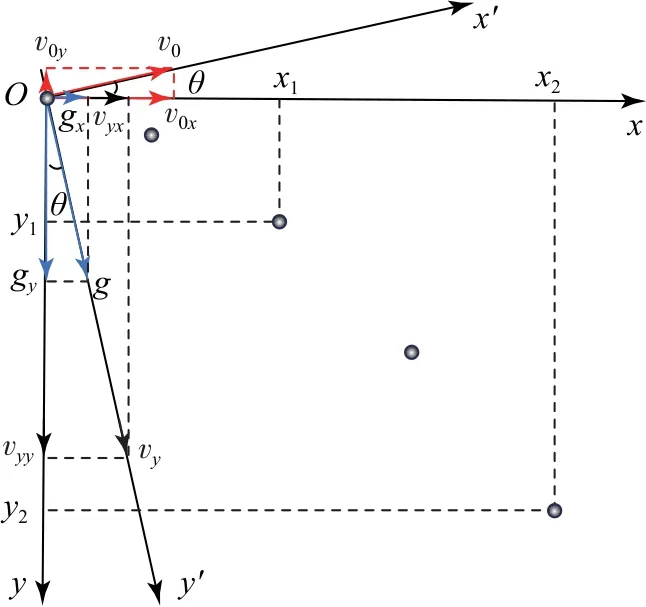
圖2
沿x軸方向,小球初速度為v0x,加速度為gsinθ,所以其在x軸上的分運動為正向勻加速直線運動,所以有x2—x1>x1,即x2>2x1.
解法1設頻閃周期為T,根據運動學規律有
解法2根據運動學規律,x軸方向有Δx=ax(2T)2,即
y軸方向有Δy=ay(2T)2,即
解法3結合推論進行解答.如圖3所示,對平拋運動沿水平方向和豎直方向建立平面直角坐標系,A、B是平拋運動軌跡上的兩點,連接OB,設OB的中點為D,則xB=2xD,因為平拋運動水平方向的分運動為勻速直線運動,所以xB=2xA,所以A與D在水平方向上的分位移相等,A與D的連線沿豎直方向.
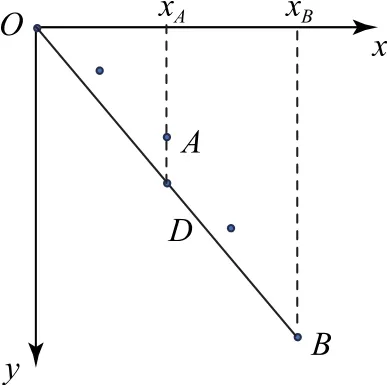
圖3
此規律也可以作為確定豎直方向的一種方法.下面就利用此方法解題.如圖4所示,連接OB,其中點為D,連接AD,AD所在直線方向即為豎直方向.
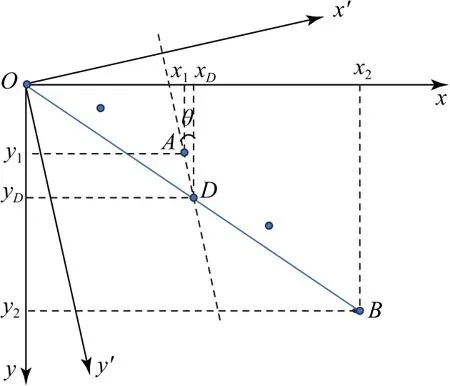
圖4
D為中點,所以有
設y與豎直方向的夾角為θ,由幾何關系可得
情況2y相對于y′向右偏,如圖5所示,設y與y′的夾角為θ.
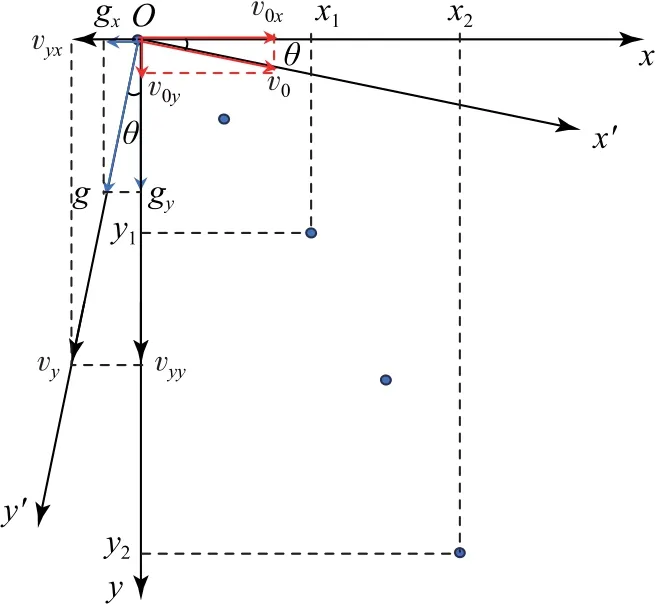
圖5
同情況1,將初速度v0、vy和重力加速度g沿x和y方向分解,g分解后有gx=gsinθ,gy=gcosθ.
沿x軸方向,加速度為—gsinθ,所以其在x軸上的分運動為正向勻減速直線運動,所以有x2—x1<x1,即x2<2x1.
解法1設頻閃周期為T,根據運動學規律有
解法2根據運動學規律,x軸方向有Δx=ax(2T)2,即
y軸方向有Δy=ay(2T)2,即
解法3如圖6所示,連接OB,其中點為D,連接AD,AD所在直線方向即為豎直方向.D為中點,所以有
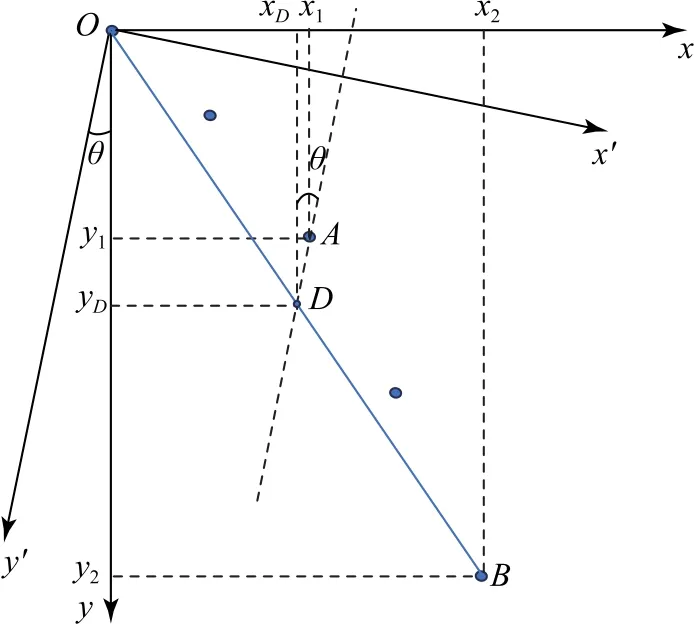
圖6
設y與豎直方向的夾角為θ,由幾何關系可得
情況1和情況2中,x2與2x1的大小關系剛好相反,但是tanθ為正值,所以兩種情況得出的結果剛好相差一個“—”號.這道題除了考查了平拋運動規律以及運動的合成與分解等相關知識,對考生的分析綜合、邏輯推理、類比遷移以及數學能力都有一定的要求,望大家在平時的學習中加強訓練,努力提升自己的綜合能力.
(完)

