輸電導線結冰數值模擬與影響因素分析

高 鵬, 臧五岳, 李丹煜, 徐 楓, 段忠東, 歐進萍

(1. 哈爾濱工業大學(深圳) 土木與環境工程學院, 廣東 深圳 518055; 2. 中國電力科學研究院有限公司 輸變電工程研究所,北京 100055)

電力工業作為一項經濟發展和人民群眾生活的支柱產業,其重要性不言而喻。對于電力傳輸來說,輸電線路是遠程輸送的主要載體。在實際運行中,輸電線路通常會受到環境因素的影響,而導線覆冰就曾給世界各地的輸電線路安全運行造成嚴重影響。如2008年南方地區歷史罕見的低溫雨雪冰凍災害天氣,造成南方電網區域4 216條輸電線路被破壞,直接經濟損失達1 100多億元,災后重建和修復改造需要資金高達390億元,受災人口達1億多人,對我國國民經濟造成了巨大損失[1]。

輸電導線覆冰通常是由于空氣中的過冷卻水滴撞擊在導線上凍結[2]。國內外學者對導線結冰展開了一系列研究。早期研究人員試圖通過對試驗數據以及自然條件的分析和總結,建立一個可以表征氣象參數和結冰量關系的公式,Langmuir等[3-5]都做過嘗試,這些經驗模型考慮的因素都比較單一,盡管從結冰概念上是正確的,但是考慮的因素過少,并不能準確地預測導線結冰。Beard等[6]通過試驗擬合得到了水滴運動受到的阻力系數。Langmuir等通過試驗將水滴中值體積直徑離散為七種不同含量的直徑,在數值模擬中應用較多,模擬結果更符合水滴碰撞特性。Fu[7]采用Beard等提出的阻力系數以及Langmuir等的尺寸分布模擬得到與試驗吻合的結冰冰形。Messinger[8]提出的結冰熱力學模型是目前研究廣泛采用的結冰模型。Macklin[9]利用風洞試驗測定旋轉圓柱體的結冰質量,定義了結冰密度計算過程中的參數。Jones[10]基于該參數提出了結冰密度的計算公式。

國內對于導線覆冰數值模型的研究起步較晚。劉和云等[11]在分析了凍雨降水產生結冰的物理過程后, 提出了一個相對簡單的結冰預測模型。孫才新等[12]在熱力學模型中考慮了電流焦耳熱的作用,進一步完善了結冰模型。郭昊等[13]基于霧凇覆冰的數值模擬方法推導了水滴碰撞特性的估算公式,提出了輸電線霧凇覆冰的工程估算方法。梁曦東等[14]提出了輸電線路時變仿真模型,可以得到時變的結冰外形和結冰質量。劉春城等[15]給出了導線均勻結冰和非均勻結冰的結冰質量和結冰厚度預測模型。Huang等[16]研究了絕緣子的結冰并針對幾何參數提出建議,減少絕緣子上的結冰。清華大學開發的三維結冰軟件AERO-ICE[17]利用歐拉方法計算水滴場,以自主開發的修正Messinger模型作為結冰熱力學分析模型。沈國輝等[18]采用有限元數值模擬方法研究導線的覆冰脫落問題,進行建模參數的敏感性分析和導線脫冰的參數分析。王昕等[19]利用覆冰導線剛性節段模型外加彈簧及配重模擬覆冰輸電線路豎向及扭轉運動動力特性,制作了D形和新月形覆冰輸電線路的氣彈模型。以上這些模型在不斷發展的過程中對推動導線結冰預測、覆冰導線舞動及冰災防治研究工作做出了積極作用。

導線結冰的研究主要有試驗和數值模擬兩種方法。風洞試驗的代價較高,在研究不同工況下結冰時比較耗時耗力。本文采用計算流體動力學 (computational fluid dynamics, CFD)數值模擬方法,基于Fluent軟件和動網格技術實現導線結冰冰形的數值模擬,研究不同條件參數對水滴運動和導線結冰特性的影響規律,著重分析了導線振動對水滴的碰撞特性和導線結冰外形的影響。

1 輸電導線結冰數值模擬方法

1.1 水滴收集系數計算

本文采用拉格朗日法計算水滴運動軌跡。通過Fluent軟件中的離散相模型(discrete phase model,DPM)[20]將水滴看成離散相,對每一個水滴的運動狀態進行跟蹤,建立水滴的運動方程。

水滴與空氣之間存在相對運動,當水滴速度小于空氣速度時,空氣對水滴的曳力成為驅動水滴運動的主要外力;當水滴速度大于空氣速度時,空氣對水滴的運動會產生阻礙作用。水滴的運動方程可以表示為

(1)

式中:mw為水滴質量;xw為水滴運動位移矢量;t為水滴運動時間;F1為水滴運動受到的阻力矢量;F2為水滴運動受到的重力矢量;ρa為空氣密度;Aw為水滴迎風面積;Cd為水滴阻力系數;ua為空氣速度矢量;uw為水滴速度矢量。阻力系數Cd根據Beard等根據球體阻力試驗數據,得到擬合函數為

(2)

式中,Re為空氣與水滴之間的相對雷諾數,可以采用如式(3)計算

(3)

式中:dw為水滴直徑;μa為空氣黏度。

計算過程中為了使DPM模型中的阻力系數與式(2)保持一致,采用自定義函數(user-defined function,UDF)修改水滴阻力加載到DPM模型中。

撞擊在導線表面的水滴數并不均勻,需要通過局部水滴收集系數來反映導線表面水滴碰撞的分布情況。局部收集系數量化了空氣來流中有多少水滴撞擊到導線表面,可以代表導線表面的水滴分布情況,是研究結冰的關鍵參數。對于水滴收集系數的計算采用粒子統計法。如圖1所示,A0為水滴釋放平面,假設其上水滴均勻分布,水滴個數為n0;A1為A0的一部分,假設其上水滴個數為n;A2為導線表面水滴撞擊網格,假設其上的水滴全部來自A1。

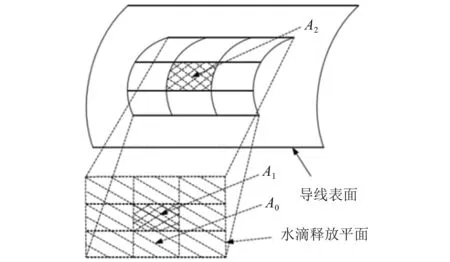
圖1 粒子統計法示意圖

水滴收集系數可以定義為釋放平面上水滴所圍成的面積與撞擊表面水滴圍成的面積之比,故可表示為

(4)

由于A0中的水滴是均勻分布的,故

(5)

代入式(5),可得

(6)

式(6)中,水滴釋放的位置和水滴個數n0由人為預先指定;撞擊網格的面積SA2通過UDF中宏函數F_AREA計算得到,撞擊網格的水滴個數n也可以通過UDF獲取并通過宏函數F_UDMI統計與存儲,該方法同樣適用于二維導線模型。

由于空氣中水滴尺寸并不是單一的,而是有一定的分散性。為了計算方便,常采用水滴中值體積直徑(mean volume diameter, MVD)。為了比較單尺寸和多尺寸的水滴碰撞特性,將水滴按照Langmuir D分布離散得到七種尺寸水滴。Langmuir D的分布如表1所示。

表1 水滴多尺寸分布表

計算多尺寸水滴收集系數方法:首先計算不同尺寸水滴各自的收集系數,該過程與計算單尺寸水滴收集系數的方法相同,即前面所述方法;其次將不同尺寸的水滴收集系數按照體積分數進行加權求和,最終得到多尺寸水滴收集系數,如式(7)所示

(7)

式中:ni為第i種尺寸水滴的體積分數;βi為第i種水滴收集系數;β為多尺寸水滴的收集系數。

1.2 導線表面結冰計算

目前,廣泛采用的結冰模型是基于Messinger思想建立的結冰熱力學模型。對于任意結冰控制體單元,需要滿足質量和能量守恒方程

Mimp+Min=Meva+Mout+Mice

(8)

Qimp+Qin+Qair=Qhtc+Qeva+Qclh+Qout+Qice

(9)

式中:Mimp為碰撞到控制體表面的液態水質量;Min為從上一個控制體流入到當前控制體的液態水質量;Meva為控制體表面蒸發的液態水質量;Mout為離開當前控制體的液態水質量;Mice為控制體內生成冰的質量;Qimp水滴撞擊到導線表面帶來的能量;Qin為從上一個控制體流入當前控制體的液態水帶來的能量;Qair為氣流氣動加熱帶來的能量;Qhtc為氣流與導線表面對流換熱帶走的能量;Qeva為液態水蒸發帶走的能量;Qclh為液態水結冰釋放的能量;Qout為離開當前控制體的液態水帶走的能量;Qice控制體內冰存儲的能量。

在結冰計算過程中假設導線表面的水滴在導線表面流動,不會發生脫落,其流動方式如圖2所示,未結冰的水滴會從駐點處平均分為兩份沿著導線表面向后流動,圖中mw為未結冰的水滴質量。

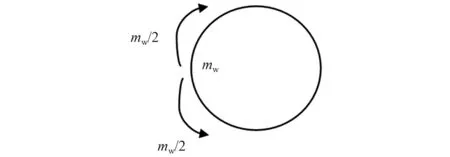
圖2 導線表面液態水滴的流動示意圖

控制體內生成冰的質量Mice的計算需要引入凍結系數f。凍結系數的定義為控制體內結冰的質量與流入控制體內所有液態水的質量之比,如式(10)所示

(10)

引入凍結系數后,結冰質量Mice可表示為

Mice=f(Mimp+Min)

(11)

得到控制體結冰質量Mice后,由式(12)計算出控制體表面結冰厚度

(12)

式中:h為控制體表面結冰厚度;ρice為結冰密度,kg/m3;Δt為結冰時間步長。

國內外學者提出過多種結冰密度計算方法,本文采用的是Jones提出的密度計算方法,其表達式為

(13)

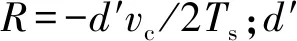
2 二維輸電導線結冰模型建立

2.1 流體計算域建立

本文選取導線直徑D為34.9 mm,采用SSTk-ω湍流模型對導線流場進行非定常計算,采用壓力為積的分離式求解器,壓力速度耦合采用壓力的半隱式方法(SIMPLEC)求解。離散相采用二階迎風格式,擴散項采用二階中心差分格式,時間離散采用二階隱式格式。利用ICEM軟件劃分網格,計算域尺寸取為30D×20D。導線中心距離入口邊界、出口邊界分別為10D,20D,距離上、下邊界均為10D。導線周圍6D×6D為非結構三角形網格加密區,外圍區域為結構化四邊形網格,網格總數為5.1×104。在導線周圍設置30層漸增的邊界層,第一層網格高度為5×10-4D,計算得到導線表面第一層網格y+的最大值為0.52。計算域和網格劃分如圖3所示。計算域左側為速度入口條件,水平速度等于來流速度;右側為出口邊界采用自由出流條件;計算域的上、下邊界采用對稱邊界條件;對于導線壁面,采用無滑移邊界條件。

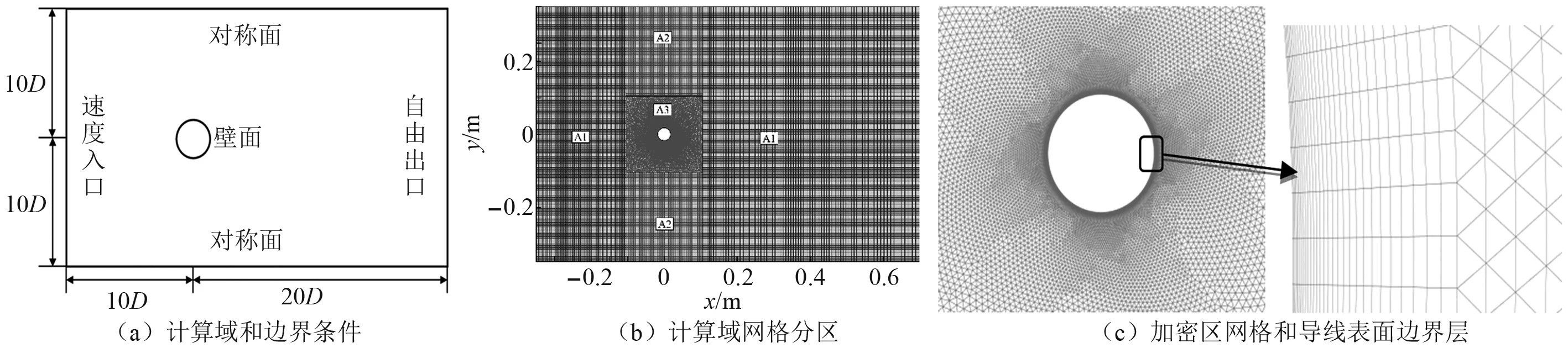
圖3 計算域、網格劃分和邊界條件

2.2 導線強迫振動模型建立

本文采用強迫振動的形式模擬導線振動,其振動的位移方程為

y=Acos(2πft+φ)

(14)

式中:y為導線橫風向位移;A為導線振幅;f為導線振動頻率;φ為初始相位。根據導線的振動位移方程可以推導出速度方程

v=2πfAsin(2πft+φ)

(15)

由于初始相位φ不會對導線的頻率及振幅產生影響,所以設定導線初始相位0。將以上速度方程通過UDF進行編程和編譯,利用CG_Motion宏實現導線的強迫振動,進而在Fluent中構建導線強迫振動模型,并求解振動導線的水滴收集系數。

導線的強迫振動通過Fluent動網格技術的動態層鋪法來實現,將計算域分為A1,A2和A3三個分區(見圖3(b))。A3分區為隨導線一起運動的加密區,A2分區為可變形區域,A1分區為固定區域,不同分區之間通過Interface邊界條件進行連接和數據傳遞。

3 計算結果分析

3.1 結冰模型驗證

3.1.1 水滴收集系數

為了驗證本文結冰數值模型的正確性,選擇了三個已有算例進行驗證分析,三個算例的計算條件如表2所示。

表2 水滴收集系數計算工況

采用本文方法計算得到不同算例下的單尺寸MVD和多尺寸水滴收集系數,如圖4所示。結果表明,多尺寸和單尺寸水滴收集系數結果整體趨勢非常接近,但在水滴撞擊的極限處,可以看出考慮了多尺寸分布后,由于存在尺寸大小不一的水滴,水滴碰撞范圍更大,與Case1的試驗值更加接近,故采用多尺寸分布對水滴軌跡的計算有一定的作用,同時也驗證了水滴計算模型的準確性。

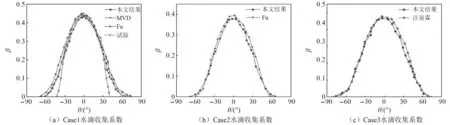
圖4 不同工況水滴收集系數

3.1.2 結冰冰形驗證

選取某個算例對結冰模型進行驗證,算例的計算條件包括導線直徑為34.9 mm,來流風速為5 m/s,環境溫度為-15 ℃,水滴直徑為35 μm,空氣含水量為1.2 g/m3。

研究共計算了30 min的結冰冰形,分為三個時間段,每個時間段的間隔為10 min。圖5給出了導線各時間段下的結冰冰形。從圖5可以看出,后一步結冰是在前一步結冰冰形上發展的,這說明結冰模擬是一個多步長的過程,需要不斷更新結冰外形進行下一時間步的計算。圖6給出了該工況下結冰30 min后的冰形與試驗以及模擬結果的對比。從圖6可以看出,本部分模型模擬的結冰形狀和現有數值模擬結果及試驗結果吻合較好。圖7所示為不同結冰時間段導線周圍時均流線圖和速度等值線圖。從圖7可以看出,不同時間段導線結冰厚度逐漸增加,導線的外形隨之發生變化,尾流時均主旋渦的形狀也由圓形逐漸拉長,時均主旋渦中心與導線中心的距離也逐漸增大。

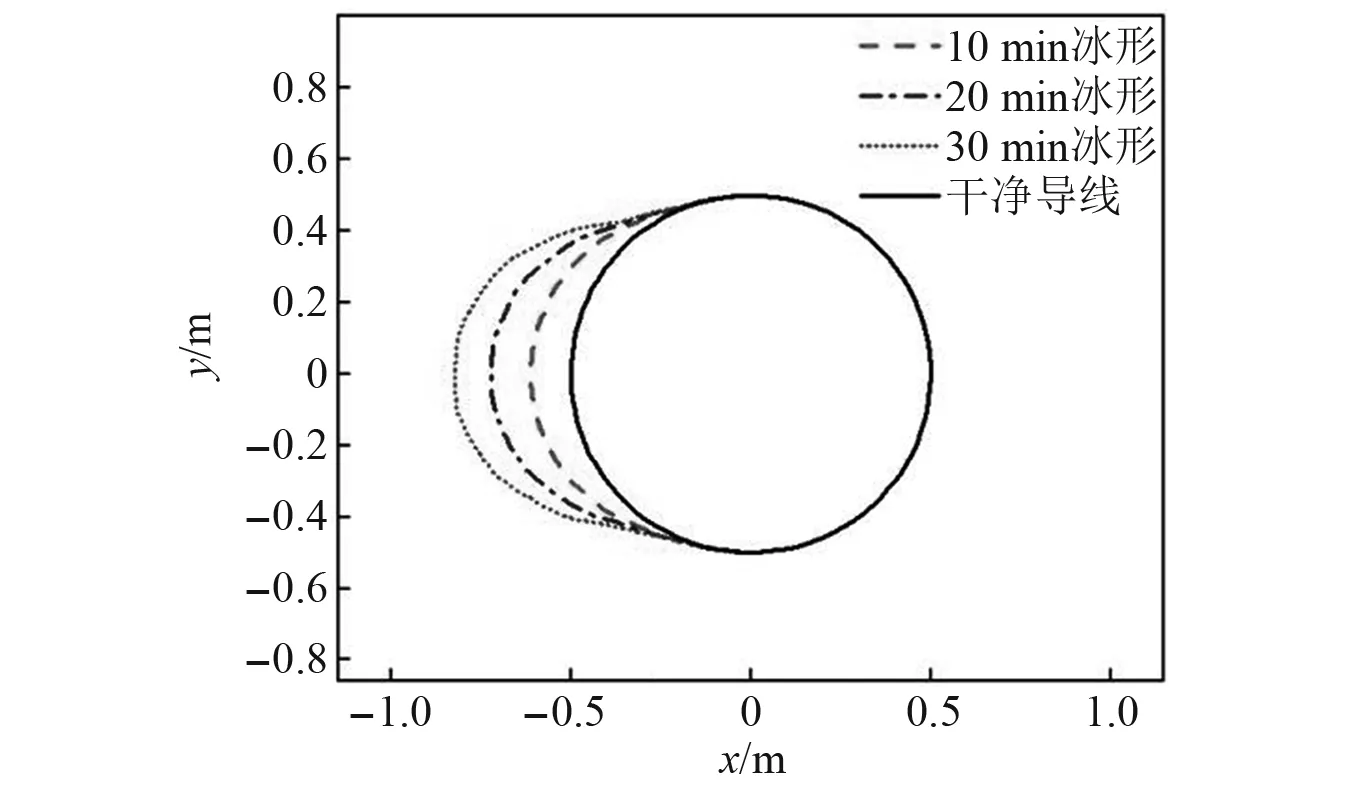
圖5 導線不同時間段結冰冰形

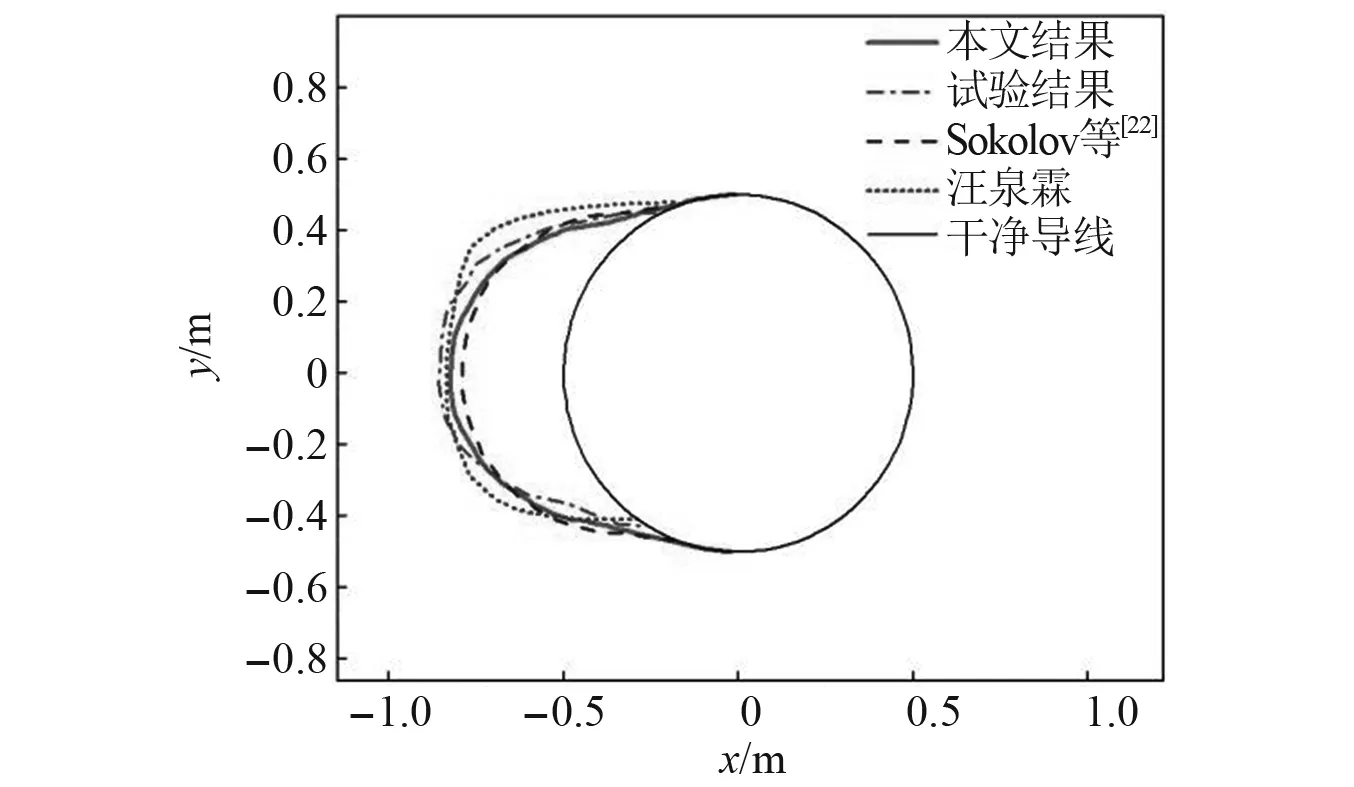
圖6 導線結冰冰形驗證

圖7 不同結冰時間段導線周圍時均流線圖和速度等值線圖

3.2 不同風速條件下的計算結果分析

風速對導線結冰的影響主要體現在對水滴收集系數的影響。隨著風速增大,水滴動能增大,水滴運動軌跡更不容易受到空氣的干擾而發生偏移,導致水滴的撞擊區域也隨之增大,并且水滴收集系數的峰值也增大。圖8給出了來流風速分別為2 m/s,5 m/s,8 m/s,12 m/s和15 m/s時導線的水滴收集系數,圖9所示為不同來流風速下的結冰冰形,其中水滴中值體積直徑為35 μm,空氣含水量為1.2 g/m3,環境溫度為-15 ℃。

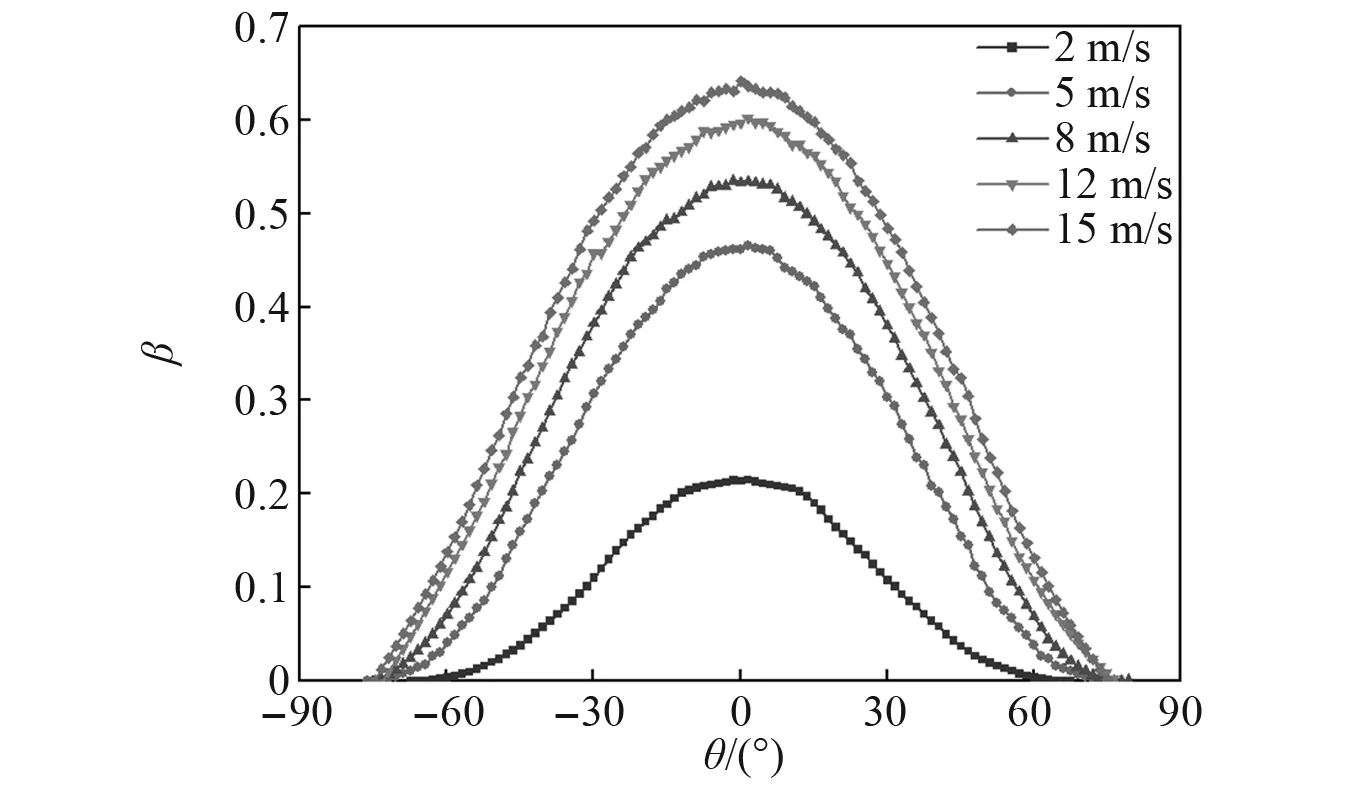
圖8 不同風速下水滴收集系數

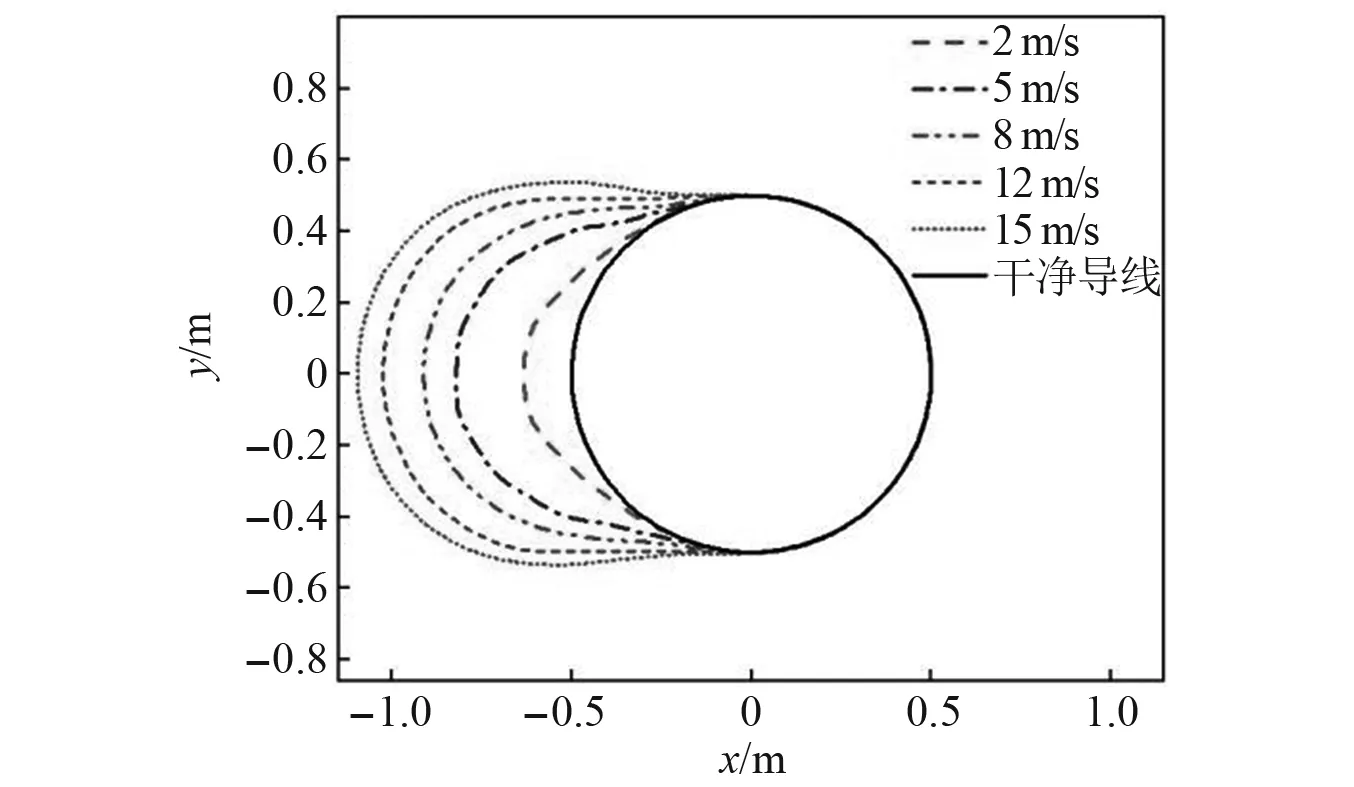
圖9 不同風速下結冰冰形

從圖9可以看出,隨著來流風速逐漸增大,導線結冰厚度不斷增加,同時導線上、下側結冰的極限位置沿著前緣駐點向后移動,結冰區域不斷增大,使得冰形看起來更為飽滿。主要原因是:由于風速的增加導致水滴收集系數增大、單位時間內被導線捕獲的水滴數增多,結冰的最大厚度也隨之增大;另一方面,由于水滴不容易偏轉,使得水滴的碰撞極限增大,導線上、下結冰極限也隨之增大。

3.3 不同環境溫度下的計算結果分析

圖10給出了風速為5 m/s,水滴中值體積直徑為35 μm,空氣含水量為1.2 g/m3,環境溫度分別為-21 ℃,-18 ℃,-15 ℃,-12 ℃,-9 ℃和-6 ℃時的導線結冰冰形,分析不同環境溫度對導線結冰冰形的影響規律。

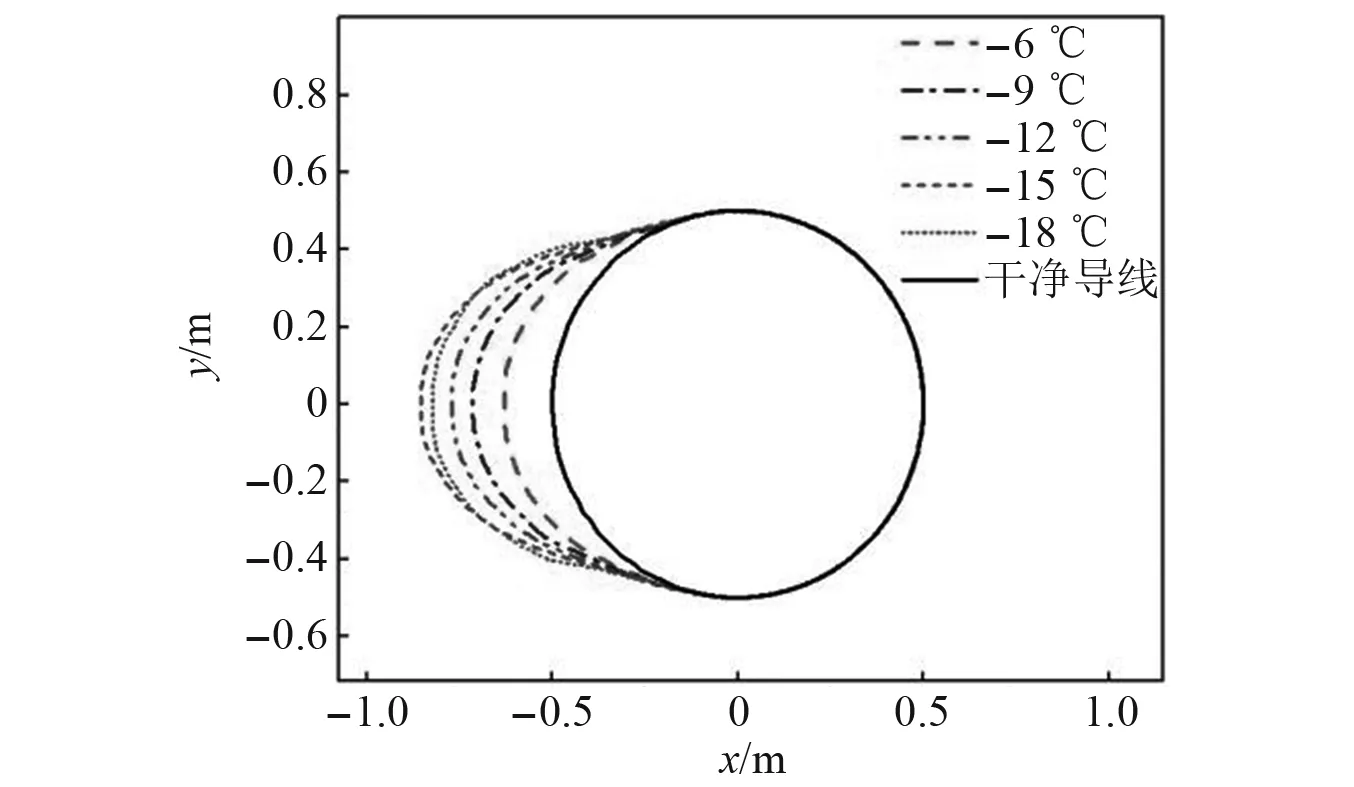
圖10 不同溫度下結冰冰形

從水滴收集系數的定義中可以知道溫度對水滴的運動幾乎沒有影響,溫度主要影響結冰時的熱力學過程。由圖10可以看出,不同溫度下的結冰范圍是一致的,但隨著溫度降低,結冰量和結冰厚度不斷增加。這是由于溫度降低增加了空氣的對流散熱,也增加了水滴碰撞到導線表面后升高至結冰溫度時吸收的熱量,導致導線表面散熱加快,從而導致單位時間內的結冰增加,并且在溫度較高時,導線表面的液態水并不能完全凍結,隨著溫度降低,凍結的水滴數越來越多,結冰厚度隨之增加。當環境溫度到達-15 ℃后,結冰厚度變化很小,這是因為此時水滴完全凍結,結冰基本不受溫度影響,溫度對結冰厚度的影響主要體現在結冰密度上,密度增加導致結冰厚度相對減少。

3.4 不同水滴直徑下的計算結果分析

結冰氣候條件下,大部分水滴的直徑在40 μm以下。圖11和圖12給出了風速為5 m/s、水滴中值體積直徑分別為15 μm,25 μm,35 μm,45 μm、空氣含水量為1.2 g/m3、環境溫度為-15 ℃時的導線水滴收集系數及結冰冰形。

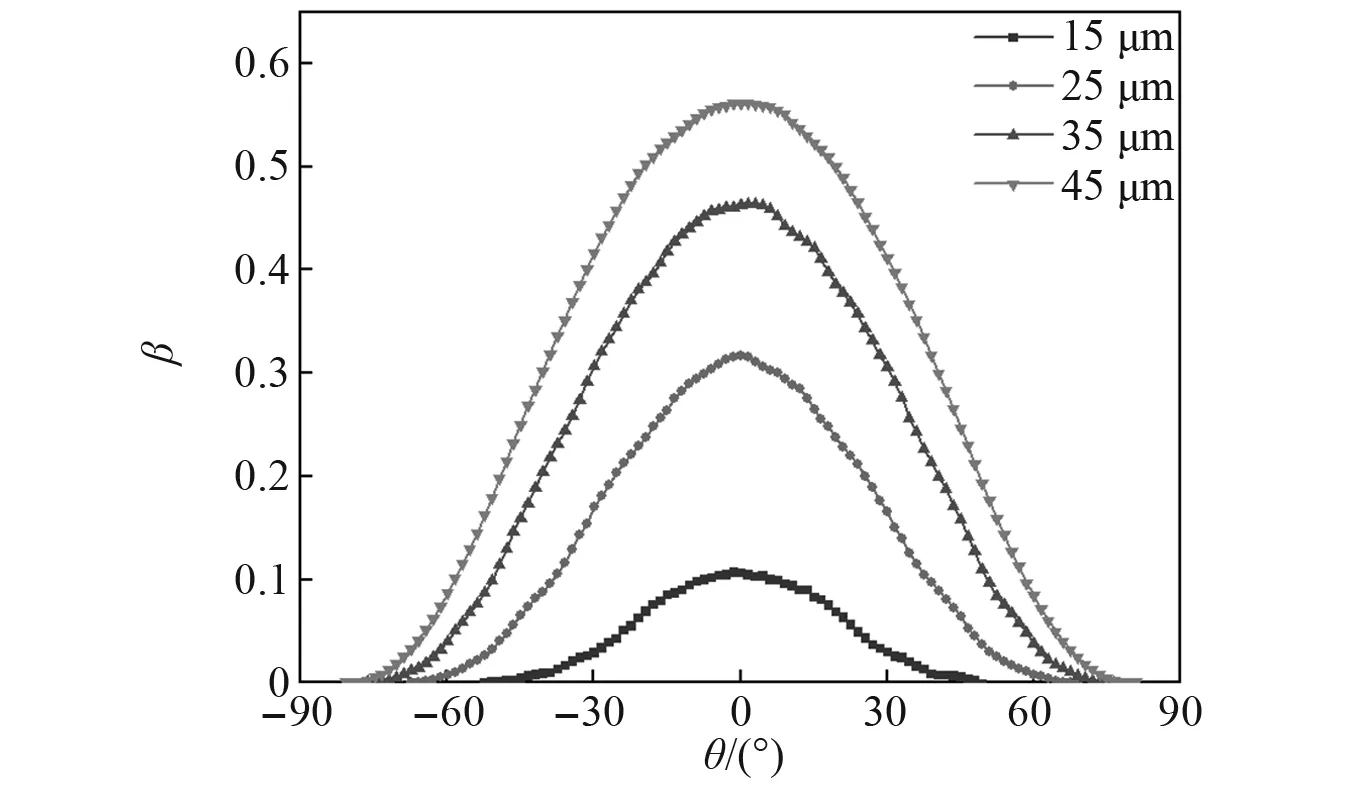
圖11 不同直徑水滴收集系數

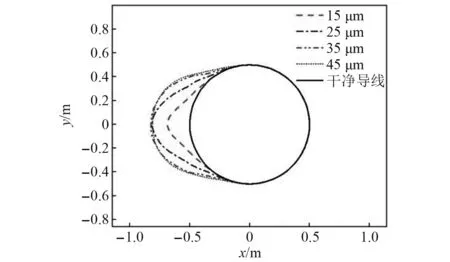
圖12 不同水滴直徑結冰冰形

從圖11可以看出,隨著水滴直徑的增大,導線表面的水滴收集系數也隨之增大。從數值上來看,最大收集系數并不是隨著水滴直徑的增大而線性增大,當水滴直徑一直增加時,導線表面的水滴收集系數增長會逐漸變得緩慢。在水滴運動過程中,直徑較小的水滴會隨著空氣一起運動而偏移導線,慣性越小受到氣流的影響就會越大。相反,較大直徑的水滴具有更大的慣性,受到氣流的影響較小,會偏離空氣流動的方向,從而碰撞到導線上。因此,隨著水滴直徑的增大,會有更多的水滴保持原有的運動軌跡從而碰撞至導線表面,水滴收集系數會整體變大,水滴碰撞范圍也會變大,上、下碰撞極限也會更遠。

從圖12可以看出,隨著水滴直徑的增加,導線表面的結冰區域增大,導線表面的結冰厚度也在增加。隨著水滴直徑的增加,導線表面前緣部分的結冰區域不斷變大,整體冰形向兩側發展。這是因為:當水滴直徑變大時,水滴運動過程中受氣流影響小,更容易被導線捕捉,進而在導線迎風側會有更大的結冰區域。

3.5 不同空氣含水量下的計算結果分析

空氣含水量(liquid water content, LWC)是衡量空氣中水滴數量的參數,決定了會發生結冰的水量多少,對導線結冰有較大影響。為了研究空氣含水量對導線結冰的影響,選取固定導線直徑為34.9 mm,風速為5 m/s,環境溫度為-15 ℃,水滴直徑為35 μm,空氣含水量分別為0.5 g/m3,1.2 g/m3,1.5 g/m3。

從水滴收集系數的定義可以知道空氣水含量對于水滴碰撞沒有影響。計算所得的導線表面結冰冰形結果如圖13所示。從圖13可以看出,導線表面的結冰量隨著空氣含水量的增大而增大,結冰厚度也隨之增加。當空氣中含水量增大時,空氣中水滴數量相對變多,單位時間內碰撞導線上的水滴數增加,最終導致導線表面結冰量變多。導線表面結冰范圍并沒有明顯變化,結冰的上、下極限位置沒有發生變化。這也是因為在只改變空氣含水量的條件下,空氣中水滴碰撞特性并沒有發生變化,水滴碰撞的極限位置也不會發生改變。

圖13 不同LWC下導線結冰冰形

3.6 不同風向角下的計算結果分析

自然界中導線受到的風向并不是固定的,本節為了研究風向對導線結冰的影響,選取了-20°,-10°,0°,10°和20°的風向角進行計算。風向角指的是來流方向和水平方向的夾角,逆時針方向為風向角的正方向,簡單示意如圖14所示[23]。導線直徑為34.9 mm,風速為5 m/s,環境溫度為-15 ℃,水滴直徑為35 μm,空氣含水量分別為1.5 g/m3。

圖14 風向角示意圖

圖15給出了導線在不同風向角下的結冰情況。從圖15可以看出,風向角對導線結冰的冰形基本沒有影響,與0°風向角下的結冰情況相似,在面對空氣來流的前緣駐點處的結冰厚度最大,從駐點沿著導線兩側向后結冰厚度逐漸減小,并且整體的冰形相似。這說明水滴會順著來流方向在導線前緣駐點處大量聚集,導致該位置處的結冰厚度最大。

3.7 導線振動下計算結果分析

3.7.1 導線振幅對結冰的影響

導線常處于微風振動狀態,其幅度通常小于導線直徑,選取導線強迫振動振幅分別為0.1D,0.5D和1.0D,導線直徑為34.9 mm,水滴中值體積直徑為35 μm,風速為5 m/s,導線振動頻率為20 Hz,環境溫度為-15 ℃,空氣含水量為1.2 g/m3。

圖16給出了水滴收集系數隨導線振動振幅增加的變化。從圖16中可以看出,隨著導線振幅的增加,導線表面的水滴碰撞極限增大。這是因為當導線沿著橫風向發生位移時,原本靜止時沒有水滴碰撞的位置會因為上、下位移與導線表面逃逸的水滴發生碰撞,從而增大水滴的碰撞極限;也正因為如此,導線上、下表面的水滴數量增多,水滴收集系數大于靜止時同位置處的水滴收集系數。在振動頻率固定不變時,雖然導線往返運動的次數不變,但是隨著振幅增大,導線每次往返運動的范圍增加,導致有更多水滴與導線上、下表面發生碰撞,所以隨著振幅增加,導線上、下表面處的水滴收集系數增加。駐點處的最大水滴收集系數下降是因為原本會碰撞到導線前緣駐點上的水滴由于導線的豎向運動而導致水滴在導線前緣駐點處發生偏移,從而導致碰撞到導線前緣駐點處的水滴數量變少,水滴收集系數因此而減小。

圖16 不同振幅下水滴收集系數

圖17所示為導線表面結冰冰形隨著振幅的變化規律。從圖17可以看出:相比于靜止導線,振動導線的結冰極限位置發生了后移,同時導線上、下表面的結冰厚度增加,這是因為導線上、下表面收集了更多的水滴,結冰量也隨之增加;而導線前緣駐點處的最大結冰厚度降低,這是因為該位置處捕捉到的水滴數量變少,凍結變小。隨著導線振幅的增加,導線上、下表面的結冰厚度由于捕捉的水滴數量增加而增大;前緣駐點處的結冰厚度由于水滴捕捉數量的不斷降低而減小。

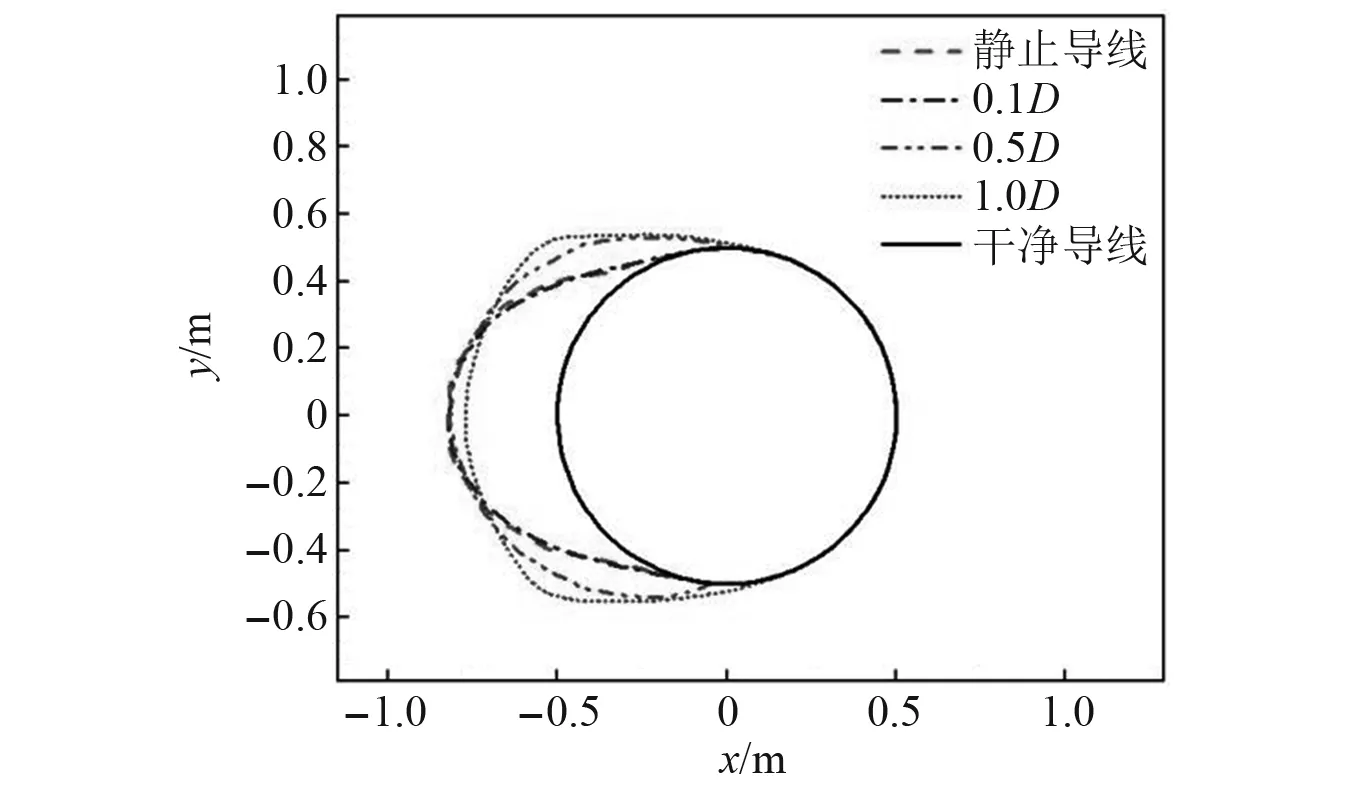
圖17 不同振幅下導線結冰冰形

3.7.2 不同振動頻率對結冰的影響

導線發生微風振動的頻率范圍約為3～100 Hz,故選取導線振動頻率分別為10 Hz,20 Hz,30 Hz,40 Hz和50 Hz五組工況進行模擬,導線振幅為1.0D,其余計算條件與前述研究相同。

圖18給出了水滴收集系數隨導線振動頻率的變化。從圖18可以看出,隨著導線振動頻率的增加,導線表面的水滴碰撞極限增大并且收集系數增大。當導線振幅固定時,隨著振動頻率的增加,導線往返運動的周期變短,因此導線在同樣的時間內做往返運動的次數增多,即導線位移的總路程變多,水滴與導線上、下表面接觸次數也變多,使得導線上、下表面捕捉的水滴數量增多,水滴收集系數隨之增大;與低頻率振動相比,頻率越高,在相同時間內導線的位移越大,可以捕捉更遠處的水滴,因此導線表面的水滴碰撞極限也變大。而前緣駐點處的水滴收集系數則因為捕捉的水滴數量減少而降低。

圖18 不同振動頻率下水滴收集系數

圖19所示為導線表面結冰冰形隨著振動頻率發生的變化。從圖19可以看出,相比于靜止導線,振動導線的結冰極限位置發生了后移,同時導線上、下表面的結冰厚度增加,這是因為導線上、下表面收集了更多水滴,結冰量也隨之增加;而導線前緣駐點處的最大結冰厚度降低,這是因為該位置處捕捉到的水滴數量變少,凍結變小。隨著導線振動頻率的增加,導線上、下表面的結冰厚度由于捕捉的水滴數量增加而增大;前緣駐點處的結冰厚度由于水滴捕捉數量的不斷降低而減小。

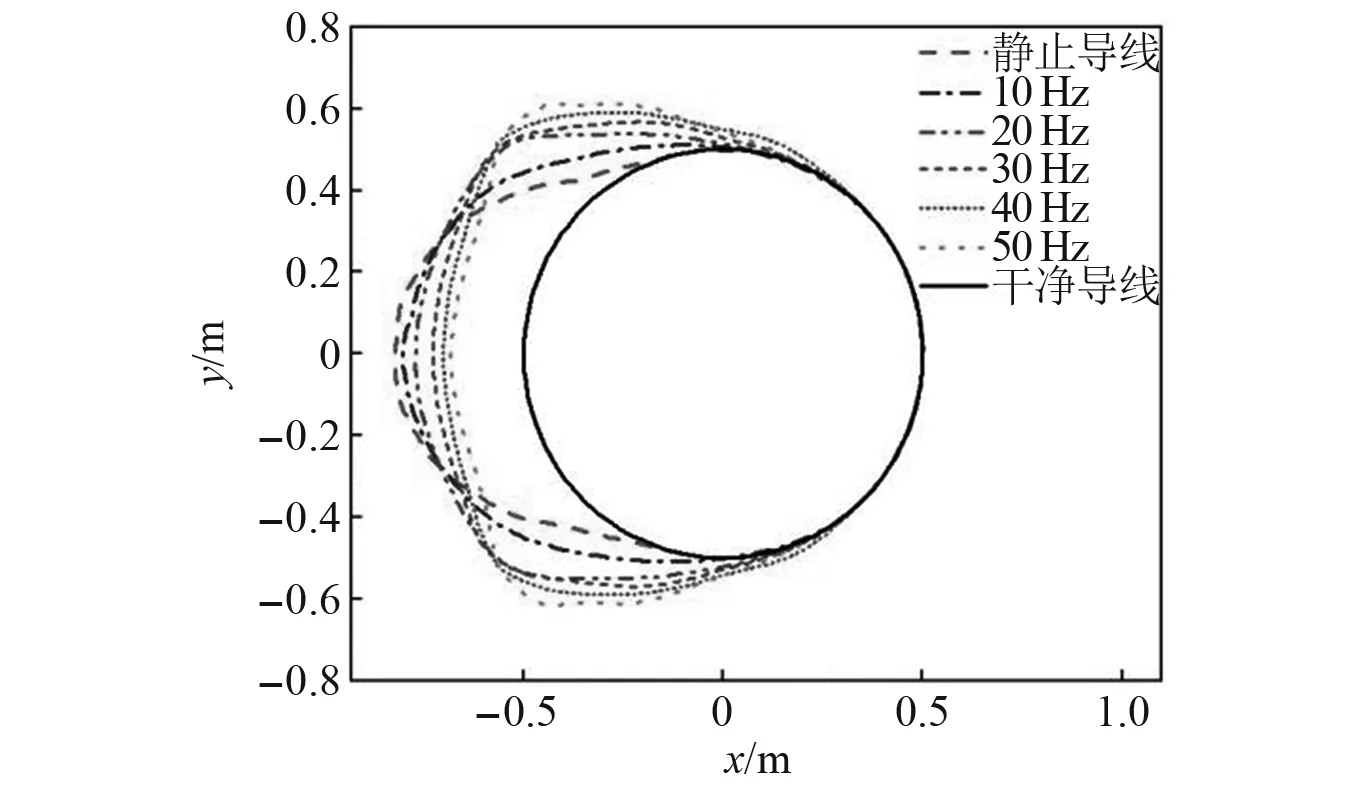
圖19 不同振動頻率下導線結冰冰形

4 結 論

本文建立基于拉格朗日法的二維輸電導線表面結冰冰形預測的CFD數值模擬方法,通過水滴收集系數和結冰冰形與現有試驗和數值模擬結果的對比分析,驗證了結冰模型的準確性,分析不同條件參數和導線振動對導線結冰特性的影響規律,得到結論如下:

(1)來流風速增大導致水滴動能增加,更多水滴撞擊到導線表面,導線表面的水滴收集系數和碰撞極限范圍增大。結冰厚度也隨著水滴收集系數的增大而增大,結冰沿著導線上、下兩側發展,冰形更為飽滿。

(2)水滴直徑增大,水滴質量和慣性增大,水滴運動狀態更不容易受到空氣干擾,導線表面能收集到更多水滴,因此導線表面水滴收集系數和碰撞極限范圍增大。結冰沿著導線上、下兩側發展,冰形更為飽滿,同時由于結冰密度的增加使得導線結冰厚度的增長并不明顯。

(3)隨著環境溫度降低,導線表面凍結水滴越來越多,結冰由濕增長轉為干增長,結冰厚度隨之增大。當溫度繼續下降(-15 ℃),此時水滴已完全凍結,主要影響結冰密度。當空氣含水量增加時,相同時間內導線表面收集到的水滴量增多,結冰厚度隨之增加。

(4)導線強迫振動振幅越大,導線的水滴收集系數最大值降低,水滴碰撞極限范圍增大,結冰厚度最大值降低,結冰逐漸向導線上、下兩側發展。導線強迫振動的頻率越大,導線前緣駐點處碰撞的水滴數越少,水滴收集系數最大值降低,導線上、下側碰撞的水滴數變多,碰撞極限范圍越大,結冰逐漸向導線上、下側發展,冰形更為飽滿。