小學(xué)數(shù)學(xué)建模教學(xué)策略探索

王一

摘要：數(shù)學(xué)是提升小學(xué)生數(shù)學(xué)思維，發(fā)展核心素養(yǎng)的重要學(xué)科。但當(dāng)前不少學(xué)生在數(shù)學(xué)學(xué)習(xí)上存在著一些問題，主要是不能恰當(dāng)?shù)剡\(yùn)用數(shù)學(xué)思想來解決問題。在教學(xué)的過程中教師可引導(dǎo)學(xué)生借助建模思想，提升解題能力，促進(jìn)全面發(fā)展。具體地說，就是教師要引導(dǎo)學(xué)生運(yùn)用數(shù)學(xué)知識解決生活中的數(shù)學(xué)問題。學(xué)生在教師的引導(dǎo)下，通過歸納、概括等手段揭示事物間的內(nèi)在關(guān)系，從而使實(shí)際問題模型化、數(shù)量化。

關(guān)鍵詞：小學(xué)數(shù)學(xué)；數(shù)學(xué)建模；學(xué)科素養(yǎng)

在當(dāng)前“雙減”的背景下，教師要減少學(xué)生課外作業(yè)的數(shù)量，減輕學(xué)生的學(xué)業(yè)負(fù)擔(dān)，就需要不斷提升他們的學(xué)習(xí)能力。但學(xué)生在實(shí)際學(xué)習(xí)的過程中更多地關(guān)注學(xué)習(xí)的結(jié)果，而不重要數(shù)學(xué)思想的運(yùn)用。教師可改變這樣的現(xiàn)狀，引導(dǎo)學(xué)生從實(shí)際情境中抽象出數(shù)學(xué)問題，進(jìn)而再解決數(shù)學(xué)問題，這能使他們初步形成模型思想，從而提升綜合運(yùn)用數(shù)學(xué)知識的能力，提高他們的核心素養(yǎng)。

一、小學(xué)數(shù)學(xué)建模教學(xué)的必要性

1.提升學(xué)生學(xué)習(xí)數(shù)學(xué)的興趣

教師在開展數(shù)學(xué)教學(xué)時(shí)首先要提升學(xué)生的學(xué)習(xí)興趣，當(dāng)學(xué)生對所學(xué)的內(nèi)容感興趣了，自然就容易投入其中，進(jìn)而主動地解決相關(guān)的問題。當(dāng)前部分小學(xué)生對數(shù)學(xué)學(xué)習(xí)不感興趣，主要是呈現(xiàn)在他們面前的是抽象的數(shù)學(xué)知識，而他們的思維卻是以形象思維為主。數(shù)學(xué)建模思想的運(yùn)用能有效地實(shí)現(xiàn)思維的轉(zhuǎn)換，提升學(xué)生解決問題的信心。基于此，教師可培養(yǎng)學(xué)生的數(shù)學(xué)建模思想，幫助他們整合數(shù)學(xué)知識，提升解決問題的能力，從而一步步地提升他們的學(xué)習(xí)興趣^[1]。

2.提升學(xué)生應(yīng)用數(shù)學(xué)的能力

教師在開展數(shù)學(xué)教學(xué)時(shí)，不但要讓學(xué)生感知教材上的基本的數(shù)學(xué)認(rèn)知，同時(shí)還要提升他們應(yīng)用數(shù)學(xué)的能力。當(dāng)前大多小學(xué)生也能記住書本上的一些認(rèn)知，也能解答書本上的相應(yīng)的問題，但是部分學(xué)生卻不能運(yùn)用所學(xué)的認(rèn)知解決實(shí)際遇到的問題，這其實(shí)就是應(yīng)用數(shù)學(xué)的能力不強(qiáng)。要改變這樣的現(xiàn)狀，教師就需要引導(dǎo)學(xué)生將所遇到的問題轉(zhuǎn)化為數(shù)學(xué)問題，再引導(dǎo)他們將數(shù)學(xué)問題與數(shù)學(xué)建模形成對應(yīng)的關(guān)系。通過這樣的引導(dǎo)，學(xué)生就很容易找到解決問題的“金鑰匙”。?“金鑰匙”的作用還在于學(xué)生可將相應(yīng)的數(shù)學(xué)建模進(jìn)一步地推廣，以解決同一類型的問題。顯然，學(xué)生應(yīng)用數(shù)學(xué)的能力在建模思想的推動下獲得新的發(fā)展。

3.發(fā)展學(xué)生多元化思維能力

教師在開展數(shù)學(xué)教學(xué)時(shí)，要以學(xué)生為主，要撥動學(xué)生思維的弦，以讓他們的思維能力得到充分地發(fā)展。但是當(dāng)前的小學(xué)數(shù)學(xué)教學(xué)還存在重結(jié)果，輕過程的現(xiàn)象，學(xué)生更關(guān)注最終的解題結(jié)果，而忽視過程中的能力發(fā)展。因此教師要改變教學(xué)的方式給學(xué)生的思維更多發(fā)展的空間，以讓他們的多元能力得到提升。如果學(xué)生要運(yùn)用建模思想解決遇到的問題，他們就需要對提取、加工與建構(gòu)信息，進(jìn)而發(fā)展概括、抽象、類比、歸納、猜想、推理等多元能。顯然學(xué)生建模的過程就是他們思維不斷提升與優(yōu)化的過程。在這個(gè)過程中學(xué)生也由原先的識記簡單的數(shù)學(xué)公式轉(zhuǎn)為理解、運(yùn)用數(shù)學(xué)建模，這促成他們的思維由低階向高階發(fā)展^[2]。

一、在觀察和探究中，提升學(xué)生自主構(gòu)建模型的能力

將建模思想運(yùn)用到小學(xué)數(shù)學(xué)教學(xué)中，對于教師來說，首先要做的就是改變原先的教學(xué)方式，不能讓學(xué)生死記硬背一些模型，再盲目地一個(gè)個(gè)地套用模型。教師要將學(xué)生當(dāng)成課堂的主人，給他們創(chuàng)設(shè)更多的應(yīng)用與實(shí)踐的空間，引導(dǎo)他們在思考和探究中自主地建構(gòu)模型。通過這樣的方式，學(xué)生能降低學(xué)習(xí)數(shù)學(xué)的難度，提升自主學(xué)習(xí)能力。 當(dāng)然在學(xué)生探究的過程中，教師也要適度地引導(dǎo)，以讓學(xué)生能構(gòu)建相應(yīng)的數(shù)學(xué)模型并順利完成自主探究的任務(wù)。

以蘇教版小學(xué)數(shù)學(xué)四年級上冊“不含括號的四則運(yùn)算”的教學(xué)為例，教師先是給學(xué)生一些題目，讓他們以自己的理解去解題，這些題目大多新舊結(jié)合，有一定的難度，但學(xué)生可以自行地完成。教師設(shè)置這部分題目，旨在引發(fā)學(xué)生建模的興趣。接著教師讓學(xué)生自主地學(xué)習(xí)課本的知識，他們要能用自己的語言將課本的基本的內(nèi)容表述出來，以讓他們獲得基礎(chǔ)的認(rèn)知。再接著，教師鼓勵(lì)學(xué)生結(jié)合教材的表述與自己所算得的結(jié)果進(jìn)行自主探究，試著構(gòu)建相應(yīng)的定理模型。一般的教學(xué)模式是學(xué)生一邊學(xué)習(xí)新的知識，教師一邊總結(jié)其中的定理。但教師可將環(huán)節(jié)交給學(xué)生，讓他們用數(shù)學(xué)語言表述出來。學(xué)生先是弄清楚一級運(yùn)算和二級運(yùn)算這兩個(gè)基本的概念，然后他們逐步理解一級預(yù)算單列式和二級預(yù)算單列式要遵循從左到右進(jìn)行運(yùn)算的定理。接著教師將下列題目呈現(xiàn)出來：50 ＋ 25 － 30；?160÷10 × 6；30 × 2－35；350 ÷ 70 ＋ 45，并提問到算式中都有哪些運(yùn)算，它們的運(yùn)算順序是什么？教師設(shè)置這樣的題目，一是引導(dǎo)學(xué)生回顧已學(xué)過的同級運(yùn)算的順序，在前兩題中學(xué)生只要按照從左往右的順序依次計(jì)算即可；二是引導(dǎo)學(xué)生在觀察中探究，學(xué)生面對的后兩題，在算式中既有加減法又有乘除法，如果含有乘法（或除法）和加、減法，他們應(yīng)先算乘法（或除法），這為后面的建模打下伏筆。顯然地，在教師創(chuàng)設(shè)的自主探究環(huán)節(jié)中，學(xué)生掌握了構(gòu)建和運(yùn)用模型的基本方法。

可見，在小學(xué)數(shù)學(xué)教學(xué)的過程中，教師要基于學(xué)生的學(xué)科素養(yǎng)開展各類教學(xué)活動，要讓學(xué)生真正地思考起來，再實(shí)現(xiàn)自主建模。

二、在問題與情境中，培養(yǎng)學(xué)生逐步感知模型的思想

當(dāng)前不少小學(xué)生的模型思想還比較薄弱，盡管他們做了不少的題目，教師也講授了不少的題目，但是在面對各種不同樣的問題時(shí)，他們不知道解決問題的切入點(diǎn)在哪兒。這樣的學(xué)習(xí)現(xiàn)狀所反映的問題其實(shí)就是學(xué)生不能將所學(xué)知識帶入模型中，再借助模型解決具體問題。基于此，教師可多創(chuàng)設(shè)不同的情境，設(shè)置不同的問題，引發(fā)他們迸發(fā)思維的火花。問題與情境的創(chuàng)設(shè)能讓學(xué)生沉浸在真實(shí)的場景中，增強(qiáng)他們解決問題的動機(jī)，學(xué)生會以情境中人物的身份從已知點(diǎn)出發(fā)探究問題，進(jìn)而主動構(gòu)建數(shù)學(xué)模型。

以蘇教版小學(xué)數(shù)學(xué)四年級下冊“運(yùn)算定律與簡便計(jì)算”的教學(xué)為例，教師先是將學(xué)生分成不同的小組，讓他們自學(xué)書本上的內(nèi)容，在相互討論與交流中弄清加法交換律、加法結(jié)合律、乘法交換律、乘法分配律、乘法結(jié)合律等基本的數(shù)學(xué)認(rèn)知。基于此，教師創(chuàng)設(shè)這樣的問題情境：甲、乙兩個(gè)工程隊(duì)合修一段路，甲隊(duì)每天修70米，乙隊(duì)每天修85米，11天正好修完。甲隊(duì)比乙隊(duì)一共少修多少米？在情境中學(xué)生可以看到修路的情境，這激發(fā)他們思考問題的欲望。大多學(xué)生先是計(jì)算出甲隊(duì)一共修了多少米，即，70x11=770米；接著他們再計(jì)算出乙隊(duì)一共修了多少米，即，85x11=935米。再接著他們列成這樣的式子：85x11=935（米）；70x11=770（米）；935-770=165（米）。教師追問這樣的計(jì)算是不是繁瑣了一點(diǎn)，能不能嘗試著運(yùn)用簡便運(yùn)算定律進(jìn)行計(jì)算？學(xué)生發(fā)現(xiàn)原來的題目可以列成這樣的式子：85x11-70x11=（85-70）×11=15×11=165。顯然地，學(xué)生發(fā)現(xiàn)這樣的計(jì)算方式要簡單一些，在具體的情境中學(xué)生更容易收獲成功。對著簡便后的運(yùn)算“（85-70）×11”，學(xué)生發(fā)現(xiàn)這其實(shí)表示的是甲隊(duì)比乙隊(duì)每天少修85-70=15（米），然后乘11，就是11天甲隊(duì)比乙隊(duì)一共少修的米數(shù)。教師通過問題情境，能引發(fā)學(xué)生進(jìn)行定向思考，他們能在實(shí)踐中一步步地找準(zhǔn)思考方向，構(gòu)建數(shù)學(xué)模型，解決真實(shí)的生活化的問題，同時(shí)又能思考建模中的數(shù)學(xué)意義。

在數(shù)學(xué)教學(xué)的過程中，教師要多創(chuàng)設(shè)一些情境，多引發(fā)學(xué)生思考。學(xué)生在思考的過程中不但能解決一些問題，同時(shí)也能發(fā)現(xiàn)一些問題，這能促進(jìn)他們不斷地探究^[3]。在探究中數(shù)學(xué)模型的思想會逐步地植根于學(xué)生的大腦，成為解決問題的重要思想。

三、在生活與實(shí)踐中，強(qiáng)化學(xué)生不斷運(yùn)用模型的能力

教師在開展數(shù)學(xué)教學(xué)的過程中，一方面要讓他們掌握一些基本的數(shù)學(xué)認(rèn)知，形成一定的數(shù)學(xué)思想；另外一方面教師要引導(dǎo)學(xué)生將學(xué)到的認(rèn)知進(jìn)行轉(zhuǎn)化，提升運(yùn)用能力與學(xué)科素養(yǎng)。但是當(dāng)前不少小學(xué)生的運(yùn)用能力不強(qiáng)，不能很好地將知識轉(zhuǎn)為能力，不能進(jìn)一步地提升解題能力。因此教師要改變教學(xué)的方式，要促進(jìn)學(xué)生運(yùn)用能力的發(fā)展。數(shù)學(xué)與生活有著密切的聯(lián)系，小學(xué)數(shù)學(xué)中與生活相關(guān)的內(nèi)容更多。教師在教學(xué)的過程中要將數(shù)學(xué)與生活連接起來，要借助生活與實(shí)踐給學(xué)生足夠的體驗(yàn)，再進(jìn)一步地提升應(yīng)用能力。在熟悉的情境中，在真實(shí)的體驗(yàn)中，學(xué)生更容易將數(shù)學(xué)知識融入其中，進(jìn)而促進(jìn)各方面能力的發(fā)展。其實(shí)對于數(shù)學(xué)模型而言，教師最要做的就是給學(xué)生更多的實(shí)踐和應(yīng)用。當(dāng)學(xué)生從生活經(jīng)驗(yàn)出發(fā)，他們更容易開展相關(guān)的探究、找尋到解決問題的路徑。總之，對接生活與實(shí)踐，教師能提升學(xué)運(yùn)用模型思想的效果，從而避免“紙上談兵”的現(xiàn)象。

以蘇教版小學(xué)數(shù)學(xué)六年級下冊《用方向和距離描述物體的位置》的教學(xué)為例，在教學(xué)這課內(nèi)容前，教師在對學(xué)生進(jìn)行家訪的時(shí)候有意了解他們的家庭住址，以及相互之間的距離。在課上，教師借助騰訊地圖將不同家庭之間、家庭與學(xué)校之間的距離與位置等呈現(xiàn)出來。教師先是對不同學(xué)生的家庭位置以學(xué)校與參照物進(jìn)行分析。接著學(xué)生一邊自學(xué)教材知識，一邊從自身的生活經(jīng)驗(yàn)出發(fā)，研究自己的家庭與班上同學(xué)的家庭之間的距離、位置等，以用方向和距離描述兩者的位置。

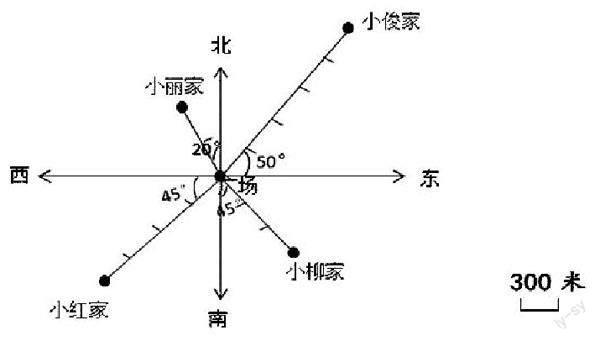
最后教師設(shè)置這樣的題目：根據(jù)以下的描述，如上圖所示，在平面圖上標(biāo)出各場所的位置。小麗家在廣場北偏西20°方向600米處；小紅家在廣場西偏南45°方向1200米處；小柳家在廣場南偏東30°方向900米處；小俊家在廣場東偏北50°方向1500米處。學(xué)生可分成不同的小組，每個(gè)成員負(fù)責(zé)標(biāo)出其中的一個(gè)場所，這樣就可以相互學(xué)習(xí)，相互發(fā)展運(yùn)用模型的能力。教師先是引導(dǎo)學(xué)生基于生活建構(gòu)模型，再基于生活創(chuàng)設(shè)場景，引導(dǎo)學(xué)生運(yùn)用建模思想解決類似的問題。

綜上所述，教師要充分了解學(xué)生的生活體驗(yàn)與實(shí)踐能力，再結(jié)合教材教學(xué)的內(nèi)容，創(chuàng)設(shè)更利于學(xué)生應(yīng)用數(shù)學(xué)模型應(yīng)用機(jī)會。數(shù)學(xué)模型是基本的數(shù)學(xué)思想，是新課標(biāo)中提出的十個(gè)核心概念之一。對模型的建構(gòu)與運(yùn)用是一個(gè)循序漸進(jìn)的過程，教師要創(chuàng)設(shè)真實(shí)的情境，讓學(xué)生在充分體驗(yàn)、積極探究中，逐步地提升這方面的能力。

結(jié)束語：總之在小學(xué)數(shù)學(xué)教學(xué)的過程中，教師要提升學(xué)生的學(xué)習(xí)能力，向他們滲透數(shù)學(xué)建模思想是非常有效的方式。當(dāng)學(xué)生在解決數(shù)學(xué)學(xué)習(xí)中的一些問題時(shí)，運(yùn)用數(shù)學(xué)語言、符號、圖像等數(shù)學(xué)模型，能提高實(shí)踐應(yīng)用能力，進(jìn)而開闊數(shù)學(xué)知識的視野，促進(jìn)數(shù)學(xué)思維能力的發(fā)展。因此教師要強(qiáng)化學(xué)生的建模思想，以讓他們在解決問題的過程中形成良好的思維品質(zhì)，為后繼的數(shù)學(xué)學(xué)習(xí)提供永不枯竭的動力。

參考文獻(xiàn)：

[1]魏得虎.如何讓模型思想滲透到小學(xué)數(shù)學(xué)教學(xué)中[J].試題與研究，2022（09）：59-60.

[2]黃麗娟.淺談小學(xué)數(shù)學(xué)教學(xué)中模型思想的融入策略[J].考試周刊，2021（07）：66-67.

[3]?郭海軍.小學(xué)數(shù)學(xué)教學(xué)中數(shù)學(xué)模型思想的融入方法教學(xué)[J].天津教育. 2022（14）?：13-15.