高中數學中探究“新問題”的策略

韓靜波 石麗娜

(人大附中北京經濟技術開發區學校)

數學學習的重要作用之一是引導學生學會思考,幫助學生積淀,形成數學思維模式.在高中階段,這種數學思維模式主要表現為從特例入手、嘗試性探索和歸納猜想一般規律或結論.本文將進一步探討如何從特例入手、嘗試性探索和歸納解決“新問題”的思路和方法,其中“新問題”是指學生感覺不熟悉、比較新穎、不容易找到解題突破口或難以形成解題思路的問題.

1 探究“新問題”的策略

合情推理具有猜測和發現新結論、探索和提供解決問題的思路和方法的作用.在探究“新問題”時,若缺少觀察、試驗、歸納、類比、聯想、猜測的思維過程,就不善于應用合情推理探索問題的規律.因此,下面探討如何利用合情推理——歸納和類比,探究“新問題”.

1.1 歸納的應用策略

歸納是特殊到一般的推理,當我們遇到“新問題”時,可以通過觀察研究一些特例,并總結特例蘊含的一般規律,猜測一般結論或總結解決此問題的一般方法,思維過程如圖1所示.

圖1

上述思維過程是從觀察、試驗、歸納反思,到再觀察、再試驗的循環往復過程,這是一個需要多次觀察試驗、逐步深化認識規律的過程,其具體策略如下.

1)從已知條件出發尋找特例,正向歸納規律

復雜、困難的問題其規律往往隱藏于一些特例之中,因此面對“新問題”,應該引導學生將已知條件特殊化,并從特殊的情況開始,逐個分析嘗試總結規律,并根據總結的規律,進一步改進特例繼續分析探究規律.筆者通過例1,總結選取特例及研究特例的策略.

例1 已知數列{an}滿足,k∈N?),[an]表示不超過an的最大整數(如[1.6]＝1),記bn＝[an],數列{bn}的前n項和為Tn.

(1)若數列{an}是公差為1的等差數列,求T4;

(2)若數列{an}是公比為k＋1 的等比數列,求bn.

(1)T4＝6(求解過程略).

(2)方法1 對k歸納

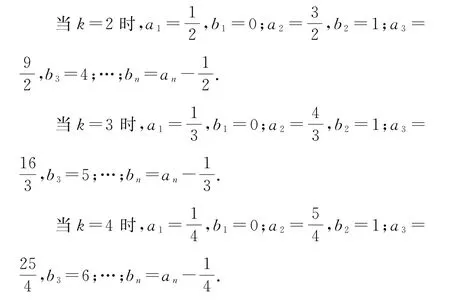
猜想:對任意的k≥2,k∈N?,有

方法2 對n歸納

猜想:對任意的k≥2,k∈N?,有

方法3 演繹推理

由例1可知,困難問題的解決往往在于解決好特殊、簡單的特例,且特例的尋找不是隨意的,而是建立在思考的基礎上,是有策略的.一方面,開始尋找的特例應該是特殊的、簡單的,即特例與已知條件聯系緊密,容易尋找和研究,并且有時需要多個特例;另一方面,需要研究特例的簡單性質,并在特例的性質中找到一般規律.

2)從結論出發假設、試驗,反向歸納規律

逆向思維是一種很重要的推理方式,當解決問題遇到困難時,從反面思考往往能幫助我們取得突破,在進行歸納推理時也是如此,除了從已知條件尋找、分析特例,還可以從結論出發,合理假設、試驗,反向歸納規律.下面筆者通過例2,總結反向歸納策略.

例2 某學校運動會的立定跳遠和30s跳繩兩個單項比賽分成預賽和決賽兩個階段,表1為10名學生的預賽成績,其中有三個數據模糊.

表1

在這10名學生中,進入立定跳遠決賽的有8人,同時進入立定跳遠決賽和30s跳繩決賽的有6人,則( ).

A.2號學生進入30s跳繩決賽

B.5號學生進入30s跳繩決賽

C.8號學生進入30s跳繩決賽

D.9號學生進入30s跳繩決賽

由表1可知,進入立定跳遠決賽的為1至8號學生,因為同時進入立定跳遠決賽和30s跳繩決賽的有6人,所以1至8號學生中有6人進入跳繩決賽,即有2人被淘汰.

首先從已知條件出發找出特殊數據,即較低的幾個30s跳繩成績為60,63,a,a－1;其次從結論出發假設試驗,對以上特殊數據進行嘗試與推理.假設30s跳繩成績為63的學生被淘汰,則30s跳繩成績為60也一定被淘汰,因此被淘汰的學生至少有3人,這與“1至8 號學生中有6 人進入跳繩決賽”矛盾,所以30s跳繩成績為63的學生(即1號和5號)進入跳繩決賽,故選B.

正難則反是一種重要的思維方式,從正反兩方面全面分析問題也是良好的思維習慣,因此對“新問題”進行觀察歸納時,學生除了從已知條件出發正向尋找、分析特例,還可以從結論出發假設、試驗,從反面歸納規律.

1.2 類比的應用策略

類比是特殊到特殊的推理,當遇到“新問題”時,可以聯想與“新問題”具有相似特征的“舊問題”(即已解決問題),然后遷移“舊方法”,即嘗試用解決“舊問題”的方法解決“新問題”,思維過程如圖2所示.

圖2

由上可知聯想“舊問題”與遷移“舊方法”,是做好類比的關鍵.下面筆者通過例3,總結聯想“舊問題”與遷移“舊方法”的策略.

例3 6名學生在畢業聚會活動中進行紀念品的交換,任意兩名學生之間最多交換一次,進行交換的兩名學生互贈一份紀念品,已知6名學生之間共進行了13 次交換,則收到4 份紀念品的學生人數為( ).

A.1或3 B.1或4

C.2或3 D.2或4

記這6名學生為a,b,c,d,e,f.由“任意兩名學生之間最多交換一次”聯想到“任意兩名學生之間交換一次”.

表2

“任意兩名學生之間最多交換一次,共交換13次”與上述理想情況差了2次,有如下兩種可能.

三人之間少交換2次,不妨設a與b,c各少交換一次,交換情況如表3所示.

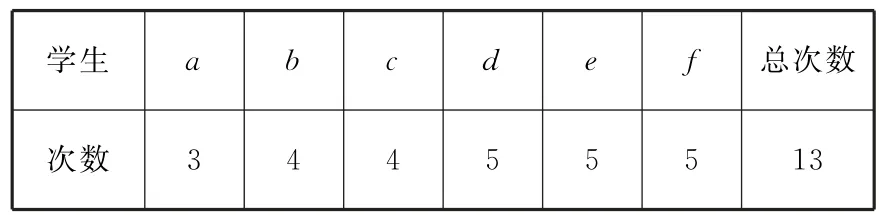
表3

四人之間少交換2次,不妨設a與b,c與d各少交換一次,交換情況如表4所示.

表4

綜上,收到4份紀念品的學生人數為2或4.

由“新問題”聯想到“舊問題”,需要將“新問題”特殊化、理想化、簡單化,即將問題轉化為特殊且容易解決的問題.本題將“任意兩名學生之間最多交換一次”類比為“任意兩名學生之間交換一次”;另一方面,遷移“舊方法”需要找出“新”與“舊”的差異,處理好差異,問題也就隨之解決.

2 策略的應用

例4 (2022年北京卷15)已知數列{an}的各項均為正數,其前n項和Sn滿足an?Sn＝9(n＝1,2,…).給出下列四個結論:

①{an}的第2項小于3;

②{an}為等比數列;

③{an}為遞減數列;

④{an}中存在小于的項.

其中所有正確結論的序號是_________.

題目有對“雙基”的考查,但主要考查學生的思維,考查學生如何思考問題,考查學生的邏輯推理素養.

1)基于“雙基”的初步信息加工

根據基礎知識和基本方法對已知、未知條件進行初步的分析,具體思考如下.

a)因為數列{an}的各項均為正數,所以數列{Sn}是各項均為正數的遞增數列;

b)因為an＞0,Sn＞0,an?Sn＝9(n＝1,2,…),所以an越大,Sn越小,an越小,Sn越大;

c)由an與Sn的關系

可將an?Sn＝9(n＝1,2,…)轉化為通項的關系或轉化為前n項和的關系.

由b)或c)都可以判斷③是否正確,由b)可以建立對④的直觀認識.

2)基于合情推理的進一步探究

對于an?Sn＝9(n＝1,2,…),依次令n＝1,n＝2,可求得a1,a2,由此可判斷①正確.

對②和④進行假設、試驗.

對于②,若通過計算an歸納驗證其是否正確,計算量大,耗時多,易出錯,因此從結論出發假設、試驗,反向歸納規律.假設②成立,根據a22＝a1a3,求出a3,驗證其是否滿足an?Sn＝9(n＝1,2,…),以此類推歸納規律.

對于④,直接歸納或證明都比較困難,因此從結論出發假設、試驗,反向歸納規律.假設{an}中不存在小于的項,即(n＝1,2,…),則可用反證法證明④的正確性.

由題意可知?n∈N?,an＞0,所以?n∈N?,Sn＋1＞Sn＞0.

綜上,正確結論的序號是①③④.

例5 (2020年北京卷21)已知{an}是無窮數列,給出兩個性質:

①對于{an}中任意兩項ai,aj(i＞j),在{an}中都存在一項am,使得

②對于{an}中任意項an(n≥3),在{an}中都存在兩項ak,al(k＞l),使得

(1)若an＝n(n＝1,2,…),判斷數列{an}是否滿足性質①,說明理由;

(2)若an＝2n－1(n＝1,2,…),判斷數列{an}是否滿足性質①和性質②,說明理由;

(3)若{an}是遞增數列,且同時滿足性質①和性質②,證明:{an}為等比數列.

1)基于“雙基”的初步信息加工

根據基礎知識和基本方法對已知、未知條件進行初步分析,具體思考如下.

考慮aj,ai,am是否成等比數列,首先要考慮ai,am能否為0,由性質①可知{an}中任意一項都不為0,因此在上式中ai,am不為0;其次考慮aj,ai,am是否為三項,即m是否等于j或i;再次通過觀察每一問的條件,發現前兩問的具體數列都是遞增正數列,所以,則m＞i＞j,第(3)問的條件“{an}是遞增數列”和前兩問是一致的,但能發現研究的一個重要問題就是“{an}各項的正負”,再結合第(3)問的結論“{an}為等比數列”可猜測數列{an}各項同時為正或同時為負(需要證明),無論哪種情況都可證出重要的結論:若,則ai＞ai,所以m＞i＞j.

2)基于合情推理的進一步探究

a)對數列{an}的特殊化.

本題分層設問,逐層遞進,前兩問將{an}具體化,從某種意義上就是引導學生從特例中理解抽象的性質①和性質②,又由上述分析可以看出第(3)問的條件“{an}是遞增數列”和前兩問是一致的,因此也可由前兩問的特殊數列發現第(3)問的一些規律,比如,若,則,所以

b)對性質①和性質②的特殊化.

下面驗證k＝5的情形.

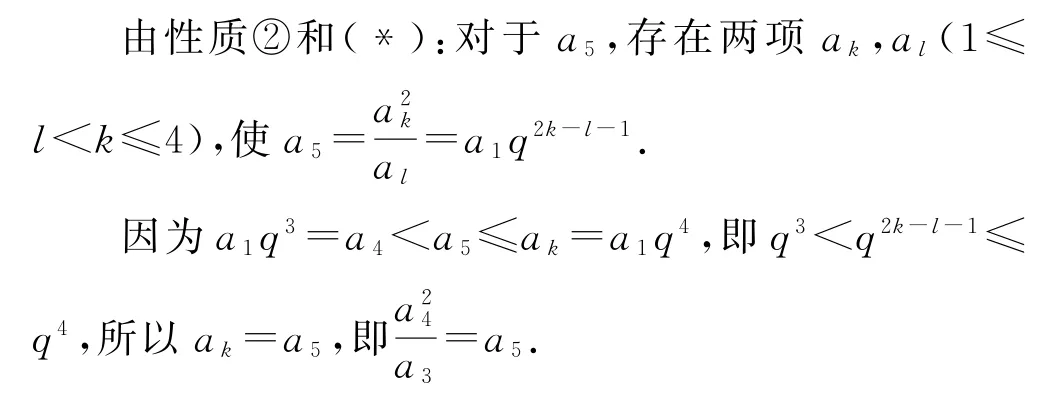
通過對性質①和性質②的特殊化,以及(?)和{an}是遞增數列,我們發現,當a1＞0,即數列{an}各項同為正時,a1,a2,a3成等比,若a1,a2,a3,…,ak成等比,性質②的作用是發現ak＋1都是以a1,a2,a3為前三項的等比數列中的項,性質①的作用是發現

上面通過歸納、類比、探究得出規律,接下來只需將規律用符號嚴格地表示出來.另外,問題還有一個難點需要解決,就是要證明數列{an}各項同時為正或同時為負,即當a1＜0,數列{an}各項均為負.此處對邏輯推理能力要求較高,而且考查創造性,可用反證法證明:假設am是一個為正的項,則m≥2且{an}只有前m－1 項為負數,由性質①可構造,這m項不同的負數,都是{an}中的項,這就與{an}只有前m－1項為負數矛盾.

假設存在n∈N?,使bn≠an,記

當a1＜0時,下證an＜0(n＝1,2,…).

假設存在n∈N?,使an＞0,記

則n1≥2,且an＜0(n＝1,2,…,n1－1),因為{an}是遞增數列,所以當n≥n1時,an＞0,當n＜n1時,an＜0.

綜上,{an}為等比數列.

題目情境新穎,求解時模式化地照搬、套用公式作用不大,只有經歷觀察、嘗試、歸納、類比、聯想、猜測等思維過程,才能找到解題突破口,這也是處理復雜、困難、陌生問題的正確思考方式,筆者認為題目的設計意圖也是考查學生是否會思考、探究新問題.

3 小結

在探究“新問題”時,要有敢于嘗試的勇氣,要有良好的思維習慣,要會思考,即從特例入手、嘗試性探索、歸納和猜想一般規律或結論,更要在平時的學習中深刻理解知識方法的本質,不斷提升能力和素養.因此,在數學學習的過程中,要注重知識的形成過程,因為知識的形成過程蘊含著數學的思維方法,體現了如何思考數學問題;其次,要注重總結如何思考問題,對于每一個問題要做好總結反思,努力做到“知其然,知其所以然,知其所以必然”;最后,還要培養敢于嘗試的勇氣,研究“新問題”時需要大膽嘗試,從特例中尋找、總結規律是必須的,也是我們解決任何困難問題需要具備的品質.

(完)