改進型免疫克隆布谷鳥算法求解軟后坐火炮多參數(shù)辨識
趙 偉,侯保林,鮑 丹
(1.南京理工大學(xué) 機械工程學(xué)院,南京 210094;2.南京理工大學(xué) 瞬態(tài)物理國家重點實驗室,南京 210094)
火炮軟后坐技術(shù)是一種減小火炮發(fā)射后坐力的專項新技術(shù)。(常規(guī)火炮在發(fā)射過程中伴隨有劇烈的沖擊與振動現(xiàn)象,與常規(guī)火炮不同,軟后坐火炮是在后坐部分向前運動的過程中進行擊發(fā),這種擊發(fā)模式利用火炮的前沖動能抵消了部分后坐能量,不僅減小火炮發(fā)射過程中的后坐力,而且同時減小火炮發(fā)射過程中的沖擊與振動。為進一步研究軟后坐火炮發(fā)射過程的運動特性,對其進行大量試驗來研究發(fā)射過程的運動特性是十分不經(jīng)濟的,因此采用構(gòu)建動力學(xué)模型進行數(shù)值仿真及試驗數(shù)據(jù)修正的方法來研究軟后坐火炮發(fā)射過程中的動力學(xué)特性是十分有優(yōu)勢的且已經(jīng)成為了首要方法[1]。但是由于軟后坐火炮的復(fù)雜結(jié)構(gòu),其發(fā)射過程的動力學(xué)模型中存在大量的未知參數(shù),并且這些未知參數(shù)的選取決定了所建立動力學(xué)模型與實際系統(tǒng)的相似程度和準確程度,因此如何準確的確定這些未知參數(shù)成為了關(guān)鍵問題。傳統(tǒng)的、單一的優(yōu)化算法在多參數(shù)辨識問題上的求解存在辨識精度低的現(xiàn)象。近些年發(fā)展出來許多辨識算法和策略來提高辨識效果。文獻[2]采用改進粒子群算法進行參數(shù)辨識,提高辨識精度;文獻[3]提出自適應(yīng)混沌變異粒子群優(yōu)化辨識方法,提高了辨識效率,縮短計算時間;但是上述算法并不能高效求解發(fā)射過程種的多參數(shù)辨識問題。
為求解軟后坐火炮發(fā)射過程的多參數(shù)辨識問題,本文提出了一種適用于求解多參數(shù)辨識問題的算法,即改進型免疫克隆布谷鳥算法(improved immune clone cuckoo algorithm,IICCA)。免疫克隆選擇算法是基于免疫系統(tǒng)的克隆選擇理論發(fā)展出來的一種智能算法[4]。基于免疫克隆選擇算法的種群刷新操作和克隆操作,該算法在求解多參數(shù)尋優(yōu)問題上具有明顯優(yōu)勢[5-6]。但是傳統(tǒng)的免疫克隆算法存在計算量大、后期收斂速度慢、存在冗余迭代等缺點。引入其他的選擇策略,結(jié)合其他算法的優(yōu)勢,可有效進一步提高免疫克隆選擇算法的優(yōu)越性。
本文針對免疫克隆選擇算法克隆種群多樣性低的問題,在更新過程中引入隨機雜交策略和高頻變異[7],提高克隆種群的局部搜索能力。針對傳統(tǒng)免疫克隆選擇算法變異概率為固定值,算法不易取得最佳概率值的問題,引入了文獻[8]的自適應(yīng)算子,自適應(yīng)算子增強了計算初期的全局搜索能力與計算后期的局部搜索能力。針對冗余計算的問題,引入精英抗體的提取算子,提高了計算效率。針對算法收斂速度慢的問題,引入疫苗接種策略[9]來提高算法的收斂速度,對疫苗接種后的抗體種群采用Lévy飛行策略和巢寄生行為[10]進行二次搜索,提高疫苗接種后種群的多樣性,從而避免由于疫苗接種策略導(dǎo)致的抗體種群多樣性下降而陷入局部最優(yōu)。同時Lévy飛行相比其余隨機搜索具有更優(yōu)秀的全局搜索能力[11],在疫苗接種后的高質(zhì)量抗體群的基礎(chǔ)上進行全局搜索,更加有利于種群向最優(yōu)解附近聚集。并且巢寄生行為本質(zhì)上是一種局部搜索行為,在高質(zhì)量的種群基礎(chǔ)上進行局部搜索,更加利于算法收斂。布谷鳥算法相比粒子群優(yōu)化算法與遺傳算法具有更高的搜索效率[12],因此將免疫克隆選擇算法與布谷鳥算法相結(jié)合比與其他算法結(jié)合將具有更高的求解效率。為驗證改進后算法的有效性,選用5個多峰測試函數(shù)對其進行驗證,將IICCA與免疫克隆選擇算法(immune clone select algorithm,ICSA)、免疫遺傳算法(immune genetic algorithm,IGA)[13]、自適應(yīng)粒子群算法(adaptive particle swarm optimizer,APSO)[14]和改進型布谷鳥算法(improved cuckoo search,ICS)[15]進行尋優(yōu)性能對比測試。
本文對軟后坐火炮發(fā)射過程進行動力學(xué)分析,建立軟后坐炮在發(fā)射過程中的動力學(xué)模型。在此基礎(chǔ)上,對動力學(xué)模型中的多參數(shù)采用IICCA算法進行辨識,并與其他4種辨識算法進行收斂速度和精度的比較,驗證IICCA算法在求解軟后坐火炮發(fā)射過程多參數(shù)辨識問題的有效性和準確性。
1 軟后坐火炮發(fā)射過程的動力學(xué)模型建立
1.1 后坐部分運動方程
軟后坐火炮的后坐緩沖裝置由兩個制退機和兩個前沖機組成。設(shè)定炮口方向為正方向,其后坐部分發(fā)射過程的運動方程為

mgsinθ-Fpt
(1)
式中:Fq為前沖機力;Fz為制退機力;Ff為由于密封裝置,前沖活塞桿與制退桿所受到的摩擦力總和;x為后坐部分的位移;sign(·)為符號函數(shù);m為后坐部分的質(zhì)量;θ為火炮射角;μ為導(dǎo)軌摩擦因數(shù);Fpt為炮膛合力。
1.2 前沖機動力學(xué)模型建立
前沖機共有兩類腔室,分別為氣體腔和液體腔。其中,液體腔又分為液體腔Ⅰ、液體腔Ⅱ和液體腔Ⅲ,前沖機結(jié)構(gòu)如圖1所示。前沖機的運動形式為桿后坐形式,即前沖活塞桿隨炮身一起運動。

圖1 前沖機結(jié)構(gòu)示意圖
前沖機力由液體腔Ⅲ的液體壓強提供,因此前沖機力的方程如式(2)所示
Fq=2pqAq
(2)
式中:pq為液體腔Ⅲ的壓強;Aq為前沖活塞的面積。
(1) 前沖過程:記圖1中前沖活塞桿的活塞尾端與流液孔Ⅰ之間的距離為L。當前沖位移x小于L時,氣體腔的壓縮氣體向右推動游動活塞,液體腔Ⅰ中液體經(jīng)由流液孔Ⅰ和流液孔Ⅲ進入液體腔Ⅱ,然后經(jīng)由流液孔Ⅱ進入液體腔Ⅲ,從而推動前沖活塞向前運動。分別列出前沖位移小于L時液體流經(jīng)流液孔Ⅰ、流液孔Ⅱ、流液孔Ⅲ時的伯努利方程如下
(3)
式中:vq1為液體在流液孔Ⅰ的絕對速度;vq2為液體在流液孔Ⅱ的絕對速度;vq3為液體在流液孔Ⅲ的絕對速度;py為液體腔Ⅰ的液體壓強;pq為液體腔Ⅲ的液體壓強;p1為液流流經(jīng)流液孔Ⅰ后的壓強;p2為液流流經(jīng)流液孔Ⅲ后的壓強;ρ為液體密度;ξq1,ξq2,ξq為前沖距離小于L時液體流過流液孔Ⅰ、流液孔Ⅱ、流液孔Ⅲ的能量損失系數(shù)。
根據(jù)連續(xù)性方程計算流各液孔的流速。
(4)
將式(3)、式(4)聯(lián)立即可求得前沖位移小于L時液體腔Ⅲ的壓強。
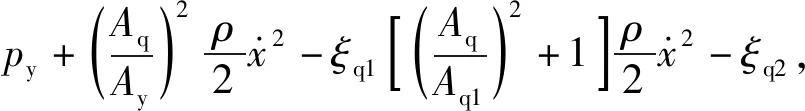
(5)
式中:Kq1為前沖位移小于L時液體流過流液孔Ⅱ的液壓阻力系數(shù),且Kq1=ξq+1;Aq1~Aq3分別為流液孔Ⅰ~流液孔Ⅲ的面積;Ay為游動活塞工作面積。
由于液體腔Ⅰ的壓強py仍是未知,因此需要對py進行求解。根據(jù)氣體腔的狀態(tài)方程、游動活塞的牛頓運動定律以及液體連續(xù)性方程推導(dǎo)液體腔Ⅰ的壓強如式(6)所示。
(6)
式中:n為氣體腔的氣體非線性指數(shù);fy為游動活塞與筒壁的摩擦力;my為游動活塞的質(zhì)量;lq0為氣體腔的初始長度;p0為氣體腔壓強。
當前沖位移x>L時,液體腔Ⅰ中的液體直接流經(jīng)流液孔Ⅰ進入液體腔Ⅲ。此時液體腔Ⅲ中壓強的公式推導(dǎo)與式(5)同理。此處推導(dǎo)過程省略,液體腔Ⅲ的壓強為

(7)
式中,Kq2為前沖位移大于L時液體流過流液孔Ⅰ的液壓阻力系數(shù)。
軟后坐火炮的復(fù)進過程與前沖過程前沖機的運動一致,方程完全相同,因此不再贅述。
(2) 后坐過程:當后坐運動剛開始時,后坐部分的位移x仍大于L,所以此時在前沖活塞的推動下,液體腔Ⅲ中的液體直接流經(jīng)流液孔Ⅰ進入液體腔Ⅰ。根據(jù)伯努利方程與連續(xù)性方程推導(dǎo)出液體腔Ⅲ的壓強為
(8)
式中,Kq3為后坐位移大于L時的液壓阻力系數(shù)。
當后坐一定距離,即后坐部分位移x (9) 式中:Kq4為后坐位移小于L時,液體流過流體孔Ⅰ的液壓阻力系數(shù);ξq3,ξq4為后坐位移小于L時,液體流過流體孔Ⅱ、流體孔Ⅳ的能量損失系數(shù);Aq4為流液孔Ⅳ的面積。 制退機由液體腔Ⅰ和液體腔Ⅱ兩個腔室組成,具體如圖2所示。制退機的運動形式為桿后坐形式,即制退桿隨炮身一起運動。 圖2 制退機結(jié)構(gòu)示意圖 制退機方程的假設(shè)條件與前沖機一致。制退機力由液體腔Ⅰ和液體腔Ⅱ的液體壓強差提供,因此制退機力的方程為 (10) 式中:Δpz為液體腔壓強差;Az為制退活塞的面積。 (1) 前沖過程:液體腔Ⅰ中的液體受到擠壓,單向閥處于打開狀態(tài),液體腔Ⅰ中的液體分兩股液流分別流入液體腔Ⅱ。一股經(jīng)單向閥的活塞口流入液體腔Ⅱ,另一股經(jīng)由筒壁溝槽流入液體腔Ⅱ。由于筒壁溝槽流口與單向閥流口的面積比接近于1∶1,因此為簡化計算,采用平均流速進行等效。根據(jù)伯努利方程推導(dǎo)制退機內(nèi)部產(chǎn)生的壓強差如下 (11) 式中:Kz1為前沖過程制退機的液壓阻力系數(shù);Az1為溝槽的流口面積;Az2為單向閥的流口面積。 (2) 后坐過程:單向閥關(guān)閉,此時液體腔Ⅱ中的液體只能經(jīng)由筒壁溝槽流入液體腔Ⅰ。筒壁溝槽在后坐部分位移x>0時是等齊溝槽,但當后坐位移x<0時,筒壁溝槽是斜坡形狀。后坐過程制退機內(nèi)部產(chǎn)生的壓強差如式(12)所示 (12) 式中:Kz2,Kz3為后坐過程液體流經(jīng)筒壁溝槽的液壓阻力系數(shù);K為制退機斜坡溝槽的形狀比例系數(shù)。 (3) 復(fù)進過程:此時制退機內(nèi)部液體流動狀態(tài)與前沖過程相同,但復(fù)進過程中的溝槽為斜面溝槽。 (13) 式中,Kz4為復(fù)進過程制退機的液壓阻力系數(shù)。 后坐部分運動方程中需要辨識的參數(shù)有導(dǎo)軌摩擦因數(shù)μ和前沖活塞桿與制退桿所受到的摩擦力Ff,參數(shù)μ和Ff的數(shù)值正確與否影響著火炮發(fā)射過程中能量損失項的計算準確性。 前沖機方程中的待辨識參數(shù)包括:前沖機的液壓阻力系數(shù)Kq1,Kq2,Kq3,Kq4,前沖機的損失系數(shù)ξq1,ξq2,ξq3,ξq4,氣體非線性指數(shù)n以及游動活塞的摩擦力fy。前沖機的液壓阻力系數(shù)和能量損失系數(shù)代表著液體流動過程中的沿程損失和局部損失。液壓阻力系數(shù)Kq1,Kq2,Kq3,Kq4和前沖機的損失系數(shù)ξq1,ξq2,ξq3,ξq4取值的準確與否影響著液體腔Ⅲ中壓強變化規(guī)律計算的準確性。n的取值影響著氣體腔壓強變化規(guī)律的求解,fy取值是否準確影響著游動活塞運動規(guī)律求解結(jié)果的準確性進而影響液體腔Ⅰ中壓強求解的正確性。 制退機方程中的待辨識參數(shù)包括:制退機液壓阻力系數(shù)Kz1,Kz2,Kz3,Kz4,制退機的液壓阻力系數(shù)取值是否準確直接決定了制退機液體腔壓強差解算結(jié)果的準確性,對火炮發(fā)射過程中制退機力的計算起著至關(guān)重要的作用。 待辨識的參數(shù)有16個,分別為Kq1,Kq2,Kq3,Kq4,Kz1,Kz2,Kz3,Kz4,ξq1,ξq2,ξq3,ξq4,n,fy,Ff,μ。待辨識參數(shù)的初始范圍如表1。 表1 待辨識參數(shù)的初始區(qū)間 參數(shù)辨識以尋優(yōu)算法為基礎(chǔ),尋找一組參數(shù)使得動力學(xué)模型的計算數(shù)據(jù)與試驗所獲得的數(shù)據(jù)的時間序列相似度的值最大,即數(shù)值仿真數(shù)據(jù)與實測數(shù)據(jù)之間的誤差最小。為了與本文算法結(jié)合,將參數(shù)辨識模型做一定轉(zhuǎn)換,轉(zhuǎn)化為求最小值的問題。其數(shù)學(xué)模型為 (14) 式中:xd為第d個待辨識參數(shù);f(xi)為仿真輸出的第i個曲線;Di為第i個試驗數(shù)據(jù)曲線;S(fi(X),Di)為第i組數(shù)據(jù)的相似度;αi為第i組數(shù)據(jù)相似度的權(quán)重系數(shù);F為性能函數(shù)。本文需要進行相似度擬合的數(shù)據(jù)一共有兩組,分別為速度和位移,因此n=2。 式(14)中相似度S綜合考慮了曲線的數(shù)值相似度與形狀相似度兩部分,相似度S的范圍為[0,1]。S=0表示兩個組數(shù)據(jù)的所有特性均不相同;S=1表示兩組數(shù)據(jù)的所有特性高度一致。曲線數(shù)值相似度是計算的兩點間的歐氏距離,曲線形狀相似度的計算依據(jù)的是界標分界法[16]。 3.1.1 算法描述 隨機產(chǎn)生規(guī)模為N的初始抗體種群X(0)= {X1,X2,…,XN}在d維搜索空間中進行搜索計算,記第i個抗體為Xi={x1i,x2i,…,xdi},i=1,2,…,N。當前抗體種群的親和度為aff={aff1,aff2,…,affN},抗體濃度den={den1,den2,…,denN},激勵度為sim={sim1,sim2,…,simN}。該算法通過對抗體種群按照激勵度從小到大排序,根據(jù)克隆算子對每個抗體逐一進行克隆,克隆完成后進行抗體隨機交叉、高頻變異、精英抗體提取、疫苗接種、免疫選擇、Lévy飛行策略、巢寄生行為和種群刷新,逐次迭代直至完成計算。算法描述如圖3所示。 圖3 算法描述 3.1.2 激勵度計算 激勵度是對抗體質(zhì)量的評價,需要綜合考慮抗體的親和度和濃度,通常親和度高和濃度低的算子激勵度較大。 simi=a·affi-b·deni (15) 式中:simi為第i個抗體Xi的激勵度;a為親和度系數(shù);b為濃度系數(shù)。對于本文參數(shù)辨識問題,親和度即為性能函數(shù)F,如式(14)。 (16) (17) 式中:N為抗體種群規(guī)模;f(Xi,Xj)為抗體相似度;δ為相似度閾值。 3.1.3 克隆算子 (18) 根據(jù)文獻[17]定義克隆規(guī)模函數(shù)。式中:Nc為克隆后的抗體種群規(guī)模;k為克隆倍數(shù),用來決定克隆種群的規(guī)模 ,k越大克隆種群數(shù)量越多;[·]為取整函數(shù)。定義克隆后的抗體種群為Xc。 3.1.4 隨機交叉、高頻變異與自適應(yīng)操作 對克隆抗體種群進行隨機交叉有利于增強種群的多樣性,為后續(xù)的變異操作提供更多的搜索中心,增強跳出局部最優(yōu)的能力。高頻變異則是在交叉運算得到的更優(yōu)抗體的基礎(chǔ)上再進行一遍局部隨機搜索。高頻變異操作的搜索范圍隨著迭代次數(shù)的增加而減小,從而使后期的搜索空間更小,提高收斂精度。針對交叉、變異概率為固定值,算法不易取得最佳概率值的問題,引入了張玲等的自適應(yīng)算子。 (1) 隨機交叉算子 (19) (2) 高頻變異算子 (20) (21) (22) 式中:rd1,rd2,rd3,rd4為隨機數(shù);P一般取0.5;pc為交叉概率;pm為變異概率;t為當前迭代數(shù);T為總迭代數(shù);r與b1為正常數(shù)。從式(22)可以看出,隨著進化,t接近于T時,η(t)≈0,從而在進化后期進行精細搜索。 (3) 自適應(yīng)算子 (23) (24) 式中:Pc_max為交叉概率最大值;Pc_min為交叉概率最小值;Pm_max為變異概率最大值;Pm_min為變異概率最小值;affavg為平均親和度。 3.1.5 精英抗體提取算子 對變異后的抗體種群Xm進行優(yōu)質(zhì)抗體的提取,當前種群Xm中的抗體數(shù)目為Nc,從中提取依據(jù)抗體親和度排序后的前N個精英抗體參與后續(xù)的計算,提取操作避免劣質(zhì)的冗余計算,縮短計算時間。 (25) 3.1.6 疫苗接種與免疫選擇 待接種的疫苗是根據(jù)先驗知識和問題背景從克隆抗體種群中提取出來的最優(yōu)抗體,將其存儲在記憶細胞中備用,記為V=(V1,V2,…,Vd)。疫苗接種是將待接種疫苗依據(jù)接種概率與精英抗體上部分基因進行替換。免疫選擇即對比子代與父代抗體的親和度,若抗體親和度提升,則保留,反之舍棄。 疫苗接種如式(26)所示 (26) 3.1.7 Lévy飛行策略和巢寄生行為 引入布谷鳥搜索算法(cuckoo search,CS)的Lévy飛行策略和巢寄生行為將有利于提高疫苗接種后種群的多樣性,避免陷入局部最優(yōu),同時在高質(zhì)量種群基礎(chǔ)上的二次搜索更有利于向最優(yōu)解靠近。 (1) Lévy飛行策略 XLi=Xvi+αLévy(λ)·(Xvi-Xbest) (27) (28) (2) 巢寄生行為 Xi=XLi+r(XLj-XLk)?H(pa-r) (29) 式中:r~U(0,1)為隨機縮放因子;?為點乘積;H(·)為Heaviside函數(shù);pa為發(fā)現(xiàn)概率,通常取0.25;XLj,XLk為隨機選取的互不相同的抗體。 3.1.8 抗體種群刷新與合并 抗體種群的刷新為在全局范圍內(nèi)隨機生成N個抗體組成一個新種群Xn,從而達到大范圍全局搜索的目的,防止抗體種群陷入局部最優(yōu)。新生成的新種群,按照親和度排序,取前N/2個與巢寄生行為更新后的抗體種群X中的前N/2個進行融合。 步驟1初始化,生成初始抗體種群X。 步驟2計算初始抗體種群X的激勵度。 步驟3按照激勵度對X抗體中進行排序,然后進行克隆操作,生成克隆抗體種群Xc,提取疫苗V。 步驟4對克隆抗體群Xc進行隨機雜交和自適應(yīng)變異操作,得到新抗體種群Xm。 步驟5對抗體種群Xm進行精英抗體提取操作得到新的抗體種群Xe。 步驟6對抗體群Xe進行疫苗接種操作,獲得Xv,然后對其進行免疫選擇。 步驟7對Xv進行Lévy飛行全局搜索更新操作生成新的種群XL,對XL進行巢寄生行為局部搜索操作生成抗體中群X。 步驟8種群刷新生成Xn,將Xn與X抗體種群按親和度進行排序,將各自前N/2個抗體進行融合,生成最終的混合種群X。 步驟9判斷是否滿足停止條件,不滿足執(zhí)行。 IICCA算法的流程框圖,如圖4所示。 圖4 IICCA算法的流程框圖 為了驗證所提出的IICCA的性能,將IICCA與ICSA,IGA,APSO和ICS進行對比。5個多峰標準測試函數(shù)如表2所示。各算法的仿真參數(shù)如下:IICCAPm_max=0.7,Pm_min=0.1,Pc_max=0.7,Pc_min=0.3,a=2,b=1,δ=0.3,k=0.5,pv=0.6,b1=2,r=0.5,α=1;在ICSA中,pm=0.7,δ=0.3,k=0.5,a=2,b=1,pa=0.25,α=1;在IGA中pm=0.7,pc=0.2,pv=0.6,δ=0.3,k=0.5,a=2,b=1;在APSO中c1=c2=2,wmax=0.7,wmin=0.4;在ICS中αmax=0.5,αmax=0.01,pαmax=0.5,pαmin=0.005。各算法的最大迭代步均為300,尋優(yōu)維數(shù)為15維。將5種優(yōu)化算法在5個標準測試函數(shù)上進行50次尋優(yōu),測試結(jié)果如表3所示,進化曲線如圖5~圖9所示。上述5個測試函數(shù)形態(tài)復(fù)雜,都是較為復(fù)雜優(yōu)化問題,具有很好的測試性能,可以有效的驗證IICCA的收斂速度和精度、全局收斂性能和多峰尋優(yōu)能力。 表2 標準測試函數(shù) 表3 算法測試結(jié)果 圖5 Ackley函數(shù)的動態(tài)尋優(yōu)過程 圖6 Griewank函數(shù)的動態(tài)尋優(yōu)過程 圖7 Lévy函數(shù)的動態(tài)尋優(yōu)過程 圖8 Rastrigin函數(shù)的動態(tài)尋優(yōu)過程 圖9 Schwefel函數(shù)的動態(tài)尋優(yōu)過程 由表3中數(shù)據(jù)可以分析出IICCA算法對上述5種多峰尋優(yōu)函數(shù)均具有較高的計算精度,且計算時間明顯低于IGA,計算精度明顯高于其他4種算法。相比經(jīng)典ICSA,本文提出的算法計算精度得到了明顯提升。雖然對于免疫克隆選擇算法引入了疫苗接種、高頻變異、布谷鳥算法等,但是算法的計算時間并未明顯增加,表明該算法在滿足計算快速性的同時提高了收斂速度和精度。由表中的標準差分析可知,IICCA算法的穩(wěn)定性很好,同比其他4種算法穩(wěn)定性具有明顯優(yōu)勢。 由圖5~圖9可知,IICCA的全局尋優(yōu)性能優(yōu)于其他4種算法,且收斂速度更快。IICCA尋優(yōu)時20代之內(nèi)就可收斂。在圖7中,對于Levy函數(shù),雖然IICCA前期的下降速度比IGA慢,但是150代之后,IGA的收斂速度明顯趨于平緩,IICCA仍然處于快速收斂狀態(tài),最終IICCA的收斂精度明顯高于IGA。在圖9中,對于Schwefel函數(shù),IICCA算法的精度明顯高于其他4種算法。本文算法將ICSA進行改進后與CS算法進行融合,顯著提升了算法的性能,新算法IICCA明顯優(yōu)于原本的ICSA與CS算法,同時也優(yōu)于一些其他的改進算法。 綜上所述,本文所提出的IICCA算法具有更高的收斂精度,更快的收斂速度,以及更優(yōu)的全局尋優(yōu)能力,完全符合工程實踐的精度要求。 本文以某大口徑軟后坐火炮發(fā)射試驗為例,設(shè)定軟后坐火炮初始位置為原點,炮口方向為速度正向,采樣頻率為10 000 Hz。試驗采集到的數(shù)據(jù)有后坐部分的位移和后坐部分的速度。測試結(jié)果曲線如圖10、圖11所示。測試數(shù)據(jù)1和測試數(shù)據(jù)2為同種試驗條件下測得的數(shù)據(jù),測試數(shù)據(jù)1和測試數(shù)據(jù)3為不同前沖擊發(fā)位置條件下測得的數(shù)據(jù)。 圖10 后坐部分速度測試曲線 圖11 后坐部分位移測試曲線 將IICCA用于軟后坐火炮發(fā)射過程參數(shù)辨識時,利用測試數(shù)據(jù)1為辨識目標值,測試數(shù)據(jù)3的用于辨識驗證,獨立進行5次參數(shù)辨識。根據(jù)式(14),參數(shù)辨識后速度曲線與位移曲線的性能函數(shù)F的平均值為0.029 8,相似度為97.02%。經(jīng)過辨識后得到上述16個參數(shù)的辨識結(jié)果如表4所示,參數(shù)辨識后的后坐部分速度曲線見圖12,位移曲線如圖13所示。由圖12和圖13可知,辨識曲線與測試曲線具有較高的相似度,辨識結(jié)果可靠。 表4 辨識參數(shù)結(jié)果 圖12 測試速度與辨識速度對比曲線 圖13 測試位移與辨識位移對比曲線 為了進一步驗證本文提出算法的優(yōu)越性,將ICSA,IGA,ICS,APSO與IICCA分別用于軟后坐火炮試驗數(shù)據(jù)的參數(shù)辨識,分別獨立運行10次后取均值,進化代數(shù)300代,其余參數(shù)均與前文選取一致。獲得的各算法參數(shù)辨識性能函數(shù)進化曲線如圖14。由圖14可知,IICCA收斂速度比其他4種算法快,收斂精度也是最高的。因此本文的IICCA較于其他算法更適用于多參數(shù)辨識的問題。 圖14 性能函數(shù)收斂曲線對比 根據(jù)牛頓動力學(xué)方程和伯努利方程建立了軟后坐火炮發(fā)射過程的動力學(xué)模型,針對火炮發(fā)射過程中,未知參數(shù)多,辨識困難的問題,對免疫克隆選擇算法引入自適應(yīng)算子,疫苗接種策略、高頻變異、隨機交叉和精英提取算子,提高了原算法的收斂速度和計算精度,再與布谷鳥算法相結(jié)合,提出了一種新算法,即改進型免疫克隆布谷鳥算法。通過對IICCA算法的研究和軟后坐火炮發(fā)射過程的參數(shù)辨識,獲得了以下結(jié)論: (1) IICCA算法在求解測試函數(shù)時,計算結(jié)果表示,IICCA算法尋優(yōu)能力明顯優(yōu)于其他4種算法和單一類型的尋優(yōu)算法,IICCA算法具有收斂速度快,計算精度高、全局搜索能力強的特點。測試結(jié)果還表明該算法的計算時間并沒有明顯的增加,因此滿足計算快速性的要求。 (2) 辨識結(jié)果表明,IICCA算法在求解軟后坐火炮多參數(shù)辨識問題時,收斂速度明顯快于其他4種算法,收斂精度也較高。因此該算法在求解多參數(shù)辨識問題時,具有明顯的優(yōu)勢。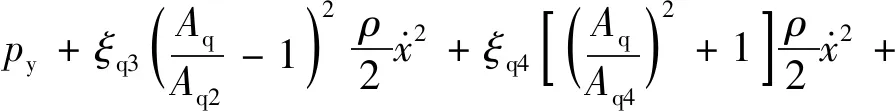
1.3 制退機動力學(xué)模型建立

2 軟后坐火炮發(fā)射過程參數(shù)辨識問題描述
2.1 軟后坐火炮待辨識參數(shù)描述

2.2 參數(shù)辨識問題數(shù)學(xué)模型
3 改進型免疫克隆布谷鳥算法模型及流程
3.1 改進型免疫克隆布谷鳥算法模型




3.2 改進型免疫克隆布谷鳥算法流程

4 IICCA性能分析與對比







5 基于試驗數(shù)據(jù)的參數(shù)辨識驗證
5.1 軟后坐火炮發(fā)射試驗
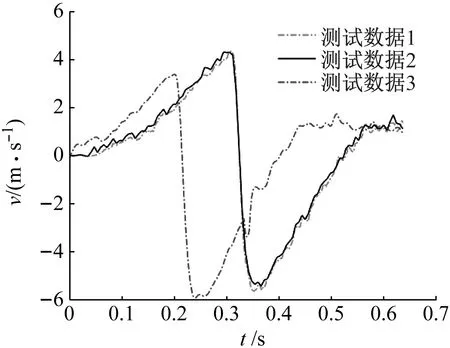

5.2 參數(shù)辨識結(jié)果

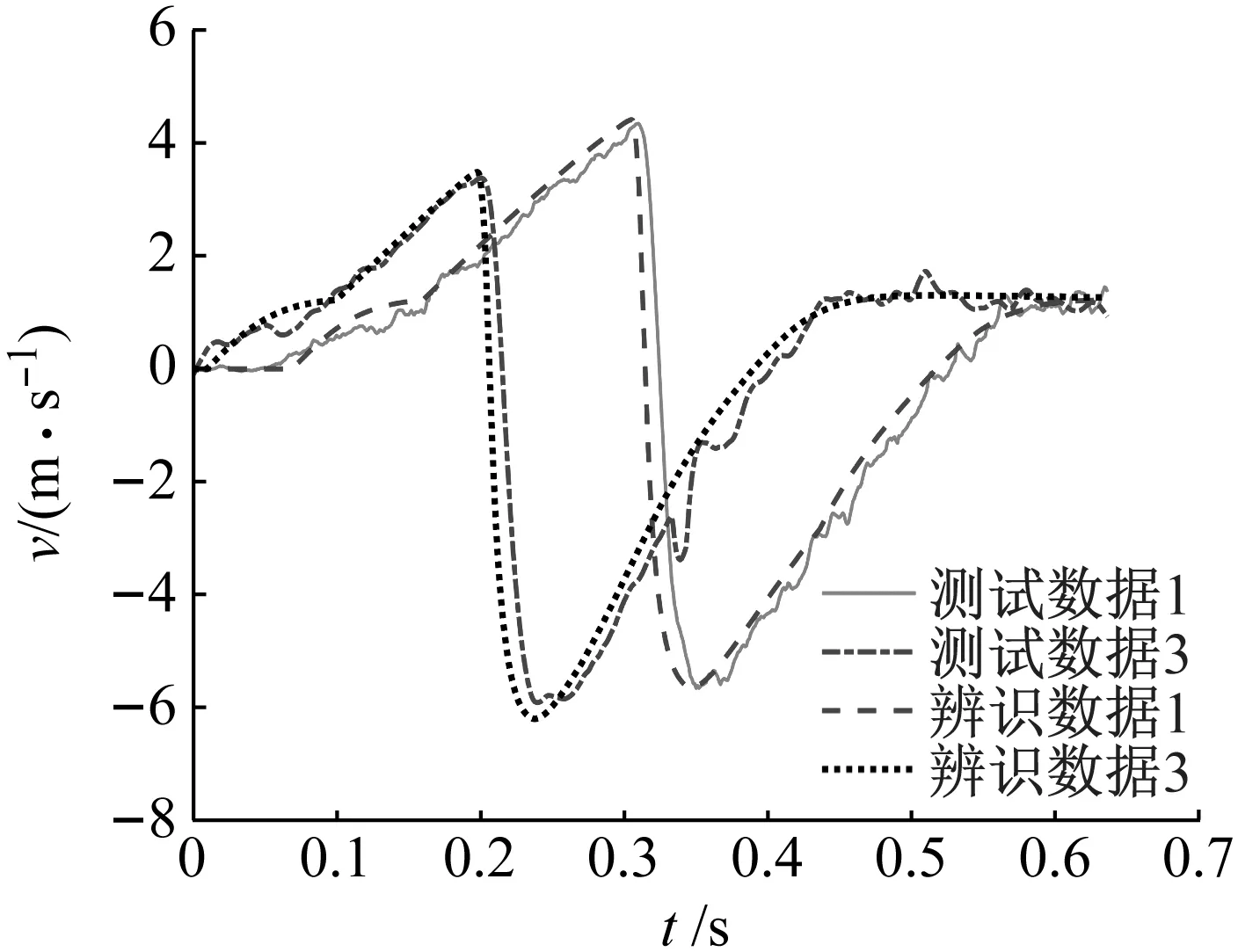

5.3 參數(shù)辨識算法比較

6 結(jié) 論

