基于一維高階梁理論的薄壁箱梁非線性彌散波特性

譚敏堯,郭德全,楊 強,楊 莉,羅德寧

(成都信息工程大學 自動化學院,成都 610225)

薄壁箱梁在工程領域內有廣泛的應用,在進行屈曲穩定分析時可知,薄壁箱梁不僅承受靜力屈曲,很多情況下還要承受動力屈曲。應力波傳播對箱梁的沖擊屈曲有顯著影響,但由于其截面結構的變化給相關研究帶來一定的困難,因此對于薄壁箱梁的應力波問題,許多學者展開了有益的探索。傳統桿件中一維應力縱波理論,都是以桿的截面在變形后仍保持為平截面,并在平截面上只作用著均布軸向應力這一基本假定為前提的。這實際上是忽略了桿中質點橫向運動的慣性作用,因而是一種近似理論,通常稱為初等理論[1]。高頻波(短波)的傳播速度較低,而低頻波(長波)的傳播速度較高。對于線彈性波來說,任意波形的波都可以通過頻譜分析方法看作由不同頻率的諧波分量迭加組成,而不同頻率的諧波分量將按各自的相速傳播,因此波形不能再保持原形而必定在傳播過程中散開來,即發生所謂波的彌散現象。但需注意,這種由橫向慣性引起的彌散,不同于過去所述由應力-應變關系的非線性所引起的非線性本構彌散,也不同于由材料黏性效應所引起黏性彌散,這主要是桿的幾何形狀所引起的,因而稱為幾何彌散。總之,只要桿的橫向尺寸遠小于波長,桿的橫向動能便遠小于縱向動能,則桿中一維應力波的初等理論就能給出足夠好的近似結果。否則必須考慮橫向慣性所引起的波的幾何彌散。

一維構件的應力波控制方程形式簡單同時其波的傳播也較易分析,對于實心截面梁的縱波和扭轉波的解可以通過D’ Alembert的經典方法[2]獲得。伯努利-歐拉理論預測了梁的彎曲波彌散,給出了接近無窮遠的近似相速度。為了修正上述結果,Timoshenko[3]考慮了扭轉慣量和剪切的影響,獲得了接近于精確理論的結果。由于高階梁理論考慮了高階項的影響,其求解精度比Timoshenko梁理論的求解精度更高。故本文采用高階梁理論。對于薄壁梁的一維分析,必須考慮高階截面變形,如翹曲和畸變。薄壁箱梁的三維位移由翹曲、扭轉、畸變一維變形量和常規剛體截面變形的線性組合表示。通過對截面變形模態的積或其導數形式的積分,可以將三維彈性方程簡化為截面變形量的一維控制方程。

對于實心梁,Chen等[4]建立了在單節點上計算反射波和透射波傳播的一維接觸界面模型。Chattopadhyay等[5]研究了復合結構的屈服參數對瑞利波相位和阻尼速度的影響。Mehemt等[6]提出了一種改進數學模型來研究應力波在具有功能梯度黏結層的兩圓柱體中的傳播。Dubuc等[7]提出了各向異性板中聲彈性導波的相位和群速度的解析公式,推導了應力各向異性板的能量速度表達式,并據此計算了群速度。鐘煒輝等[8]對階躍荷載作用下的軸心壓桿的動力分岔屈曲問題進行分析,獲得了沖擊分岔屈曲荷載及相應屈曲模態。

然而,目前對薄壁箱梁的波傳播研究較少,薄壁箱梁的響應受平面內變形和平面外翹曲的截面變形影響較大。Mitra等[9]運用高階插值函數的無鎖緊薄壁梁有限元來分析波在復合材料薄壁梁中的傳播,研究中他們考慮了梁單元的一階剪切變形和扭轉翹曲,但忽略了截面畸變。Gavric[10]通過殼有限元對薄壁梁的橫截面進行離散,在給定激勵頻率下計算薄壁梁的波數和模態,通過求解離散系統方程的本征值問題,發現在I型梁中畸變模態主要傳輸能量,而基本模態在高頻時消失。Houillon等[11]解決了Gavric研究的一些數值局限性,并使用有限元模型計算了包括真實汽車車身結構在內的一般截面薄壁梁的頻散曲線。Kim等[12-14]基于高階薄壁梁理論,研究了諧波激勵下無限長矩形截面直薄壁梁中扭轉波的傳播。

本文考慮了薄壁箱梁受動扭轉載荷作用時,其橫截面將產生翹曲、扭轉和畸變形變,同時各形變間將產生相互耦合。由于耦合作用,波沿軸向的傳播變得非常復雜。因此,本文通過這3種形變(翹曲、扭轉和畸變)在截面內和截面外的變形特點,運用一維高階梁理論來分析薄壁箱形梁的色散關系。

1 薄壁箱梁的基本運動方程

圖1中給出了薄壁箱梁的全局坐標系(y,z,x),O為橫截面剪切中心,并將各板的局部坐標系(s,n,x)分別給出。圖1中：s和n分別為切向和法向坐標;x為薄壁箱梁軸向坐標;b和h分別為薄壁箱梁的寬度和高度;壁厚m通常為常數且比其他尺寸小得多。薄壁箱梁在給定軸向坐標x方向的變形量由軸向位移u表示;z方向和y方向的變形量分別用w和v表示垂直撓度和橫向位移。

圖2給出3個方向的位移與各形變的關系。在計算剪應力時考慮了翹曲,軸向位移u(s,n,x)僅與翹曲相關,為翹曲函數?(x)與翹曲形變函數ψ?x(s)的乘積。在圖2的放大圖中,M0為薄壁箱梁橫截面中面上的任意一點,平面在M1點處的畸變位移可以通過忽略壁面在厚度方向上的壓縮得到。薄壁箱梁的橫截面位移w(s,n,x),v(s,n,x)都與扭轉和畸變形變相關。關于n-軸和s-軸方向的橫截面扭轉函數ψθn(s),ψθs(s)分別與與扭轉角θ(x)相乘可獲得扭轉的垂直撓度和橫向位移;同理,關于n-軸和s-軸方向的橫截面畸變函數ψχn(s),[ψχs(s)-ndψχn(s)/ds]分別與畸變角χ(x)相乘可獲得畸變形變產生的垂直撓度和橫向位移[14]。

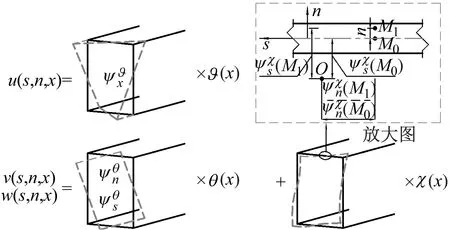
圖2 薄壁箱梁的位移與各變形關系

其中,本文的基本假設為：①在假定梁壁厚遠小于梁長的情況下,求出薄壁箱梁的位移;②在研究畸變引起的形變時,薄壁箱梁的輪廓線在每一個板上都是伸展的。

因此,薄壁箱梁橫截面中心線上任意一點的三維位移為

(1)

(2)

(3)

(4)

(5)

(6)

(7)

式中：i為各板的編號;di為截面剪切中心到第i板的法向距離。

為了獲得動力學方程,將拉格朗日變分法運用到運動方程的推導中。動能T和應變能U可分別表示為

(8)

(9)

正應變及切應變分別為

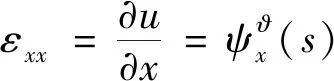
(10)

(11)

(12)

取拉格朗日泛函L的變分,可以得到運動方程

(13)

式中,A為橫截面面積。將式(1)～式(3)代入式(13),即將靜力方法推廣到動力問題

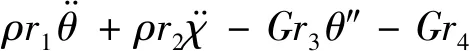
(14)

(15)

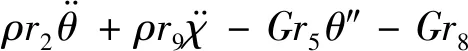
(16)

式中,截面慣性矩ri為截面形狀函數ψ的乘積對截面面積A的積分,詳見附錄A。

由于慣性矩r5=0,則一維應力可合成為

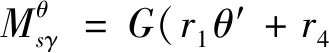
(17)

B?=Er6?′

(18)

(19)

式中,Mθsγ,B?,Mχsγ分別為扭轉翹曲力矩、翹曲雙力矩和畸變翹曲力矩。

2 彌散效應的理論分析

由于薄壁箱梁各板中潛在的波動關系可以從其橫截面的彌散效應進行理解,因此,薄壁箱梁的彌散關系可以使用第1章的方程進行理論分析。

對于彌散效應的分析,可以使用沿薄壁箱梁x軸無限長度的波速表達式,翹曲、扭轉和畸變的諧波解分別可表示為

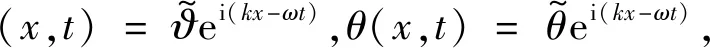
(20)

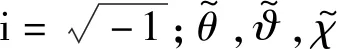
(21)

B6(k)ω6+B4(k)ω4+B2(k)ω2+B0(k)=0

(22)

其中系數B6,B4,B2,B0如下

(23)

式(22)為一個六階的色散方程,存在兩組波解,沿正軸向和負軸向傳播。本文中主要研究沿x軸正向傳播的波。在任一組解中,波數存在有實數(±Λ)、虛數(±iΓ)和復數(±(kR±iki))3個形式。前兩組是純實波數(±Λ)和純虛波數(±iΓ)分別對應的是傳播波和近場波。復波數±(kR±iki)情況稍復雜,一般情況下復波數代表隨距離衰減的傳播波,即其攜帶的能量在傳播過程中被阻尼逐步散掉。由于薄壁箱梁殼體中存在不連續區域,在不連續界面處使用連續條件時,復波數相關的波頻率較小故本文中忽略不計。

在Timoshenko梁理論中,低頻范圍內存在一對正、反向的傳播波和兩個近場波(也稱為耗散波)。k為實數時,傳播波被稱為最低形變模態分支1的波。k為純虛數時,兩個近場波被稱為正、反向衰減的耗散波。載波頻率超過截止頻率時兩對傳播波同時存在,稱為分支2和分支3模態。隨著頻率的增加,其中一列非傳播波衰減越來越慢,最終變為傳播波。

式(21)的解給出了色散關系(ω-k的關系),相速度c、群速度cg分別描述為

c=ω/k,cg=dω/dk

(27)

當k=0時,根據式(21)可以求出截止角頻率ωc和相應的截止頻率fc

(28)

(1) 當波數k趨近于0(k→0)時,分析分支1色散關系的漸近行為,在此情況下,式(21)可近似為

(29)

忽略式(29)行列式中關于翹曲與畸變的高階項,得到分支1的低頻頻散關系,即

(30)

(2) 當分支2和分支3達到截止頻率時,且波數k趨近于0(k→0)時,群速度變為0。為了更清晰地研究截止頻率附近的波,將式(21)中的波數考慮為趨近于0,可得

(31)

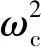
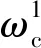
(3) 當波數趨于無窮(k→∞)時,根據式(27),將ω=kc代入式(9),3個分支的漸近行為可由相速度c表示

(32)

根據式(32)可獲得3個非零解

(33)

(34)

根據式(33)可知,波的極限速度c1,2既包含扭轉又包含畸變;極限速度c3僅與薄壁箱梁的材料屬性相關。

(35)

為了便于分析,引入翹曲-扭轉系數a?和畸變-扭轉系數aχ,相對振幅關系為

(36)

其中,

由式(35)可知,翹曲在π/2內與扭轉的相位相異,而畸變與扭轉的相位相同。

對于反向傳播波,其分析過程類似于正向傳播波。

3 算例分析

3.1 薄壁箱梁壁厚的影響(算例1)

本算例中,分析了薄壁箱梁壁厚對頻散曲線的影響。其中,薄壁箱梁的橫截面高h=0.1 m,寬b=0.05 m,壁厚m有3種情況分別為：Ⅰ,m1=0.002 m;Ⅱ,m2=0.004 m;Ⅲ,m3=0.008 m。薄壁箱梁的材料屬性：彈性模量E=2.10×1011N/m2;泊松比μ=0.3;密度ρ=7.85×103kg/m3。根據式(21)的六階色散方程,3種不同壁厚的薄壁箱梁所產生的波可分別獲得兩組波解。在本算例中,對頻散曲線的分析主要研究沿x軸正向傳播的波。每組壁厚的解分別對應3個分支,分別被稱為分支1、分支2和分支3,如圖3所示。現將頻率Ω和波數K進行歸一化處理,可得

圖3 不同壁厚的薄壁箱梁的彌散曲線

(37)

根據式(32),可以計算出各不同壁厚的薄壁箱梁的彌散波的極限速度,如表1所示。

表1 3種不同壁厚的薄壁箱梁的極限速度

本例中橫波速度cs=3 205.7m/s,為即不考慮翹曲又不考慮畸變的純扭轉波的波速。根據式(31)的第一行和第三行得到的式(33)中的兩個解,因此可轉換為即含扭轉又含畸變形變的極限速度。這兩種波的模式,扭轉和畸變形變對波行為的影響是不同的且均比橫波速度要低。根據表1可知,隨著薄壁箱梁壁厚的增加,兩個極限速度c1和c2反而減小。波速c3由式(31)第二行翹曲主導波方程得到,可以認為是翹曲波的極限速度c3=5 172.19 m/s與薄壁箱梁波速相同。翹曲主導的波在圖3中表示為分支3。

3.2 薄壁箱梁橫截面寬高比的影響(算例2)

此算例中,薄壁箱梁的材料屬性與算例1相同,其壁厚為m=0.002 m。4種不同橫截面的幾何尺寸及相應的極限速度如表2所示。圖4～圖6研究了薄壁箱梁橫截面在不同寬高比b/h下的色散曲線分支1、分支2和分支3。

表2 薄壁箱梁不同橫截面的幾何尺寸和極限速度

從圖4可知,色散曲線分支1(傳播波)的頻率隨著薄壁箱梁橫截面的寬高比b/h的降低而升高。根據圖5、圖6,分支2和分支3(耗散波)的頻率卻隨著橫截面的寬高比b/h的降低而降低。根據表2中極限速度c1和c2可知,當橫截面寬高比為1時,扭轉與畸變、扭轉與翹曲之間的耦合效應都消失,即r2=0和r4=0,分支1和分支2的相位速度在較高頻率下非常接近。由此可知,薄壁箱梁的幾何效應對非線性彌散波有較大影響。

圖7～圖9為3個分支的翹曲-扭轉相對振幅系數a?隨波數變化的變化。圖10為畸變-扭轉相對振幅系數aχ隨波數變化的變化。

圖10 畸變-扭轉相對振幅系數aχ

圖7中的分支1(傳播波)在波數為100以下時表現的翹曲與扭轉相對振幅系數較為明顯。當寬高比b/h為1/2時,最大翹曲與扭轉相對振幅系數為-0.003 3。圖8中分支2(耗散波)在波數為200以下時表現的翹曲與扭轉相對振幅系數最明顯。當寬高比b/h為1/2時,其翹曲與扭轉相對振幅系數大于其他寬高比情況下的系數,最大系數為-0.000 55。從圖7和圖8中可以明顯看出,當寬高比b/h為1時,由于翹曲與扭轉、畸變與扭轉的耦合效應消失,分支1和分支2在波數較大的情況下非常接近。圖9中分支3(耗散波)在波數600以下時翹曲-扭轉相對振幅變化都較為明顯,是3個分支中同等波數下翹曲-扭轉相對振幅數值最大的。長度比越小,分支1和分支3的翹曲-扭轉相對振幅系數越小。

圖10中分支1、分支2和分支3的畸變-扭轉相對振幅系數都相等,僅和薄壁箱梁的幾何橫截面尺寸有關。當寬高比b/h為1時,畸變與扭轉的耦合效應消失,其慣性矩r2為0,故畸變-扭轉相對振幅系數也為0。隨著寬高比的增加,畸變-扭轉相對振幅系數增大,其值主要表現為r2/r9的比值。故由此可知,畸變-扭轉相對振幅系數受到薄壁箱梁的幾何效應有效大影響。

圖7～圖10證實了波數極限分析的有效性,可知分支1、分支2和分支3中主要表現為畸變和扭轉的耦合波運動。

4 結 論

本文采用一維高階梁理論,對薄壁箱梁的扭轉、翹曲和畸變形變進行了截面內和截面外的分析,對這3種形變波的耦合傳播行為進行了理論研究。利用薄壁箱梁的運動方程解析出波的頻散曲線和群速度,并通過研究每個波支在波數下的極限行為,給出其物理解釋。在3個波的分支中,它們的高波數極限速度低于橫波速度,解析推導了翹曲與扭轉和畸變與扭轉的波幅之間的關系,并詳細分析了薄壁箱梁的幾何效應對非線性色散彌散波的影響。

附錄A 截面慣性矩

(A.1)

(A.2)

(A.3)

(A.4)

(A.5)

(A.6)

(A.7)

(A.8)

(A.9)

(A.10)

(A.11)