把握契機　滲透數學思想　發展核心素養

遲曉菲

［摘 要］數學思想是從特定的數學認識過程中產生的一些方法和觀點。核心素養是在數學學習過程中逐漸形成和發展的。數學課程要培養學生的三大核心素養：會用數學的眼光觀察現實世界、會用數學的思維思考現實世界、會用數學的語言表達現實世界。在課堂中把握契機，融入多種數學思想，使知識前后間產生聯系，讓知識簡單化、趣味化、形象化，對培養學生的核心素養和優化課堂教學都有一定的促進作用。

［關鍵詞］數學教學；數學思想；核心素養

［中圖分類號］ G623.5 ［文獻標識碼］ A ［文章編號］ 1007-9068（2023）23-0054-04

【教學內容】

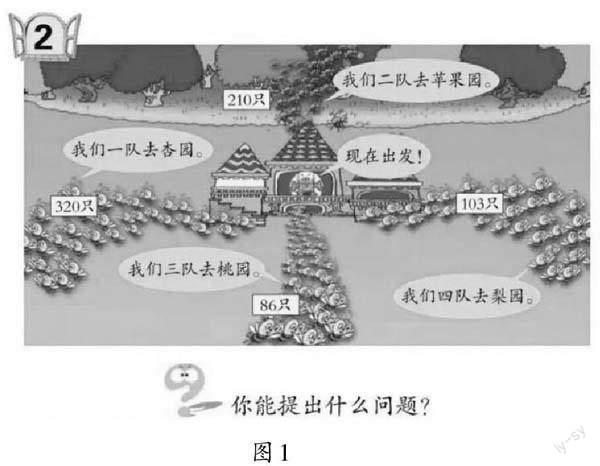
青島版教材二年級下冊第四單元（如圖1）。

【教學目標】

1.結合具體情境進一步理解加法和減法的含義；理解三位數加減兩、三位數（不進位、不退位）的算理，掌握算法。

2.經歷發現問題、提出問題、分析問題、解決問題的過程，體驗算法多樣化，培養學生初步的抽象概括能力、動手實踐能力、運算能力，使學生積累數學活動經驗。

3.在合作交流中，培養學生的數學思維；通過解決簡單的實際問題，使學生體會數學與生活的密切聯系，感受學數學、用數學的樂趣。

【教學重點】

掌握三位數加減兩、三位數（不進位、不退位）的筆算。

【教學難點】

理解筆算的算理。

【教學準備】

教具：多媒體課件、計數器、導學單。學具：計數器、鉛筆、直尺。

【教學過程】

一、創設情境，提出問題

師：同學們，春天來了，小蜜蜂們都去采蜜了。仔細觀察圖1，你能發現什么數學信息？

生1：一隊有320只小蜜蜂去杏園。二隊有210只小蜜蜂去蘋果園。

師：根據這些信息，你能提出什么數學問題？

生1：一隊和二隊一共有多少只小蜜蜂？

生2：二隊比一隊少多少只小蜜蜂？

【評析】讓學生用“數學的眼光”去觀察，引導學生提出問題，進入本節課的初始思考階段。將生活問題轉化為數學問題，讓學生感受數學與生活的聯系，體會數學來源于生活，增強他們的問題意識和應用意識。

二、合作探究，學習新知

1.結合意義，列出算式

師：要解決“一隊和二隊一共有多少只小蜜蜂？”這個數學問題，需要用到什么數學信息？誰能把信息和問題連起來說一遍？

生1：一隊有320只小蜜蜂，二隊有210只小蜜蜂，一隊和二隊一共有多少只小蜜蜂？

師：表述真清晰！怎樣列式？

生1：320+210。

師（板書）：為什么要用加法？

生1：把一隊和二隊的小蜜蜂只數合起來就要用加法計算。

師：觀察一下，這個算式和我們以前學的有什么不同？

生2：以前學的是兩位數加兩位數，這是三位數加三位數。

2.自主探索，嘗試計算

師：回想兩位數加兩位數的計算，三位數加三位數你想怎么計算？

生3：用豎式計算。

生4：口算。

生5：用撥計數器的方法計算。

師：你們知道的方法可真多！選擇你喜歡的方法，小組一起探究。

3.合作交流，感知算法

師：誰來交流？

生6：32個十加21個十等于53個十，53個十是530。

師：生6把320和210分別看作32個十和21個十，將算式轉化為兩位數加兩位數的口算。誰有不同的口算方法？

生7：3個百加2個百是5個百，2個十加1個十是3個十，5個百加3個十是530。

（板書：300+200=500，20+10=30，500+30=530）

師：把320和210根據數的組成拆分，轉化成整百數加整百數、整十數加整十數的口算。看來轉化是一種重要的數學思想。

【評析】學生的學習活動應當是一個生動活潑、主動和富有個性的過程。本環節中，教師在分析解決三位數加三位數的計算時，引導學生回憶以前學習兩位數加兩位數的計算方法，使其運用轉化思想將三位數加三位數轉化成兩位數加兩位數，或轉化成整百數加整百數、整十數加整十數的口算，利用已有的知識經驗來解決新問題，降低了問題的難度。

4.溝通優化，提升算法

師：誰是用撥計數器的方法計算的？

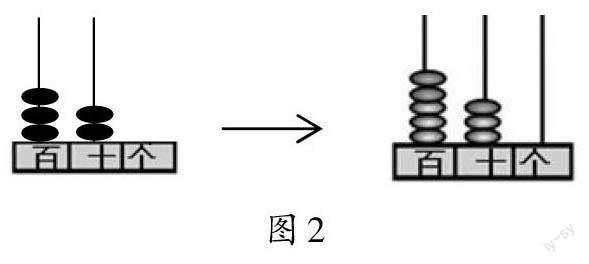
生8：我先撥320，在百位上撥3個珠子，在十位上撥2個珠子；再撥210，在百位上撥2個珠子，在十位上撥1個珠子。合起來就是530（如圖2）。

師：其他同學有什么想問的嗎？

生9：為什么百位上的后2個珠子要和前3個珠子撥在一起？為什么十位上的后1個珠子要和前2個珠子撥在一起？

生8：因為這是加法計算，所以相同數位上的珠子要撥在一起。

師：還有不同的方法嗎？

生10：我用列豎式的方法，相同數位對齊（如圖3）。

師：你們有什么想問生10的嗎？

生11：為什么3和2對齊？2和1對齊？

生10：因為3和2在百位上，都表示幾個百；1和2在十位上，都表示幾個十。

師：530中的3和5分別表示什么？怎么得來的？

生12：3表示3個十，2個十加1個十得3個十；5表示5個百，3個百加2個百得5個百。

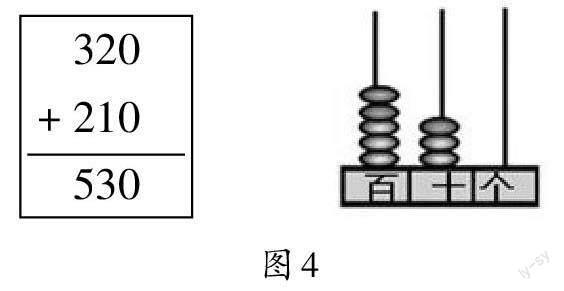
師：數形結合可以幫助我們更加形象地理解問題（如圖4）。用豎式計算時要注意什么？

生（齊）：相同數位對齊，從個位算起。

【評析】在上述教學中，學生用撥計數器的方法，直觀、形象地解決加法計算問題。在列豎式計算時，教師帶領學生規范書寫豎式，同時結合計數器，將“數”與“形”建立緊密的聯系，進而滲透數形結合思想。

5.類比遷移，探究減法

師：我們再來解決“二隊比一隊少多少只小蜜蜂？”這個問題，誰來列式？

生13：320-210。

師：怎樣解決？誰來板演？

生14：我是用豎式計算的，相同數位對齊，先算個位，0-0=0，再算十位，2-1=1，最后算百位，3-2=1，合起來是110。

師：你說得真完整。關于這個豎式，你有要提醒大家注意的地方嗎？

生14：計算時相同數位要對齊，從個位算起。

師：這是非常關鍵的一點。同學們，你們認為還有什么要注意的嗎？

生（齊）：還要注意看清加減號。

6.仿例練習，遷移運用

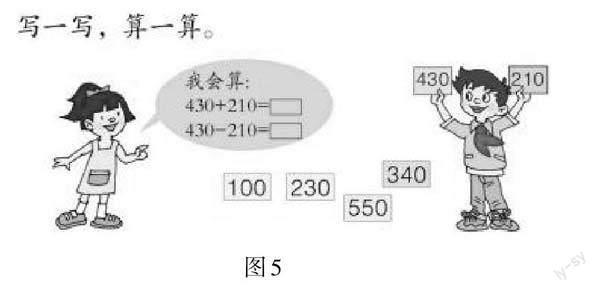
師（出示圖5）：有兩名同學在玩“抽卡片列算式”的游戲。仿照游戲，誰和同桌來試一試？

生15：我抽出卡片550和340。

生16：我列算式為550+340=890，550-340=210。

師：你是怎么算的？

生16：55個十加34個十是89個十，89個十是890；55個十減34個十是21個十，21個十是210。

【評析】《義務教育數學課程標準（2022年版）》指出，要讓學生經歷數學思考、遷移運用等學習過程，體會數學是認識、理解、表達真實世界的工具、方法和語言。上述教學中，教師引導學生在三位數加法的基礎上再次進行類比推理，認識到三位數的減法的算理與之本質是一樣的，進而真正掌握三位數減法的算法。

7.類比溝通，促進發展

（1）遷移算理，嘗試計算

師：一隊和二隊的小蜜蜂去采蜜了，三隊的小蜜蜂也不甘落后（如圖1），三隊有多少只小蜜蜂？

生（齊）：86只。

師：三隊有86只小蜜蜂，二隊有210只小蜜蜂，根據這兩個信息，你能提出一個數學問題嗎？

生17：二隊和三隊一共有多少只小蜜蜂？

師：怎樣列式？

生18：210+86。

師：仔細觀察，這個算式有什么特點？

生19：是三位數加兩位數。

師（補充課題）：這是我們今天要進一步研究的內容——“三位數加減兩位數（不進位、不退位）的筆算”。怎樣計算呢？遷移的思想可以幫助我們更好地解決問題。請類比三位數加減三位數的計算，再次小組合作探究。

（2）合作交流，理解算理

生20（上前板演）：相同數位對齊，先算個位，0+6=6，再算十位，1+8=9，最后把百位上的2落下來，合起來是296（如圖6）。

生21（質疑）：8為什么要和1對齊，而不是和2對齊？

生20：8和1都表示幾個十，所以都要寫在十位上。

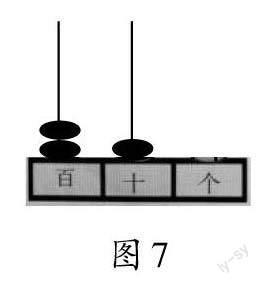
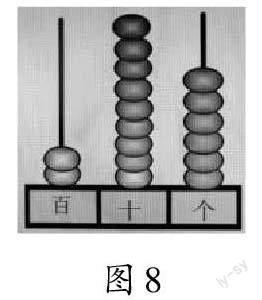
師（出示圖7）：讓我們借助計數器來理解。計數器上已撥出210，你能把計數器補充完整嗎？

生22：在十位上再撥8個珠子，個位上撥6個珠子（如圖8）。

師（小結）：同樣是相同數位上的數才能相加，數形結合讓我們理解起來更簡單。

（3）正向遷移，融會貫通

師（出示499-77）：計算并解釋算理。

生23：相同數位對齊，先算個位，9-7=2，再算十位，9-7=2，最后把百位上的4落下來，合起來是422。

師：422中兩個2表示的意思一樣嗎？分別是怎么得來的？

生24：個位上的2表示2個一，9個一減7個一得2個一；十位上的2表示2個十，9個十減7個十得2個十。

師（小結）：同一個數字在不同數位上表示的意思不同。

【評析】讓學生經歷質疑互動過程，可培養學生的問題意識和合作交流能力。學生根據前兩個問題的學習，自主探究，遷移知識。在探究中，學生由借助學具操作層面提升到算法層面，加深了對算理的理解。

三、自主練習，靈活應用

第一關：列豎式計算。

29+540= 857-37= 634+205=

師：我們了解了三位數加減兩、三位數的筆算，那么四位數加減四位數的筆算，你知道要注意什么嗎？

生（齊）：相同數位對齊，從個位算起。

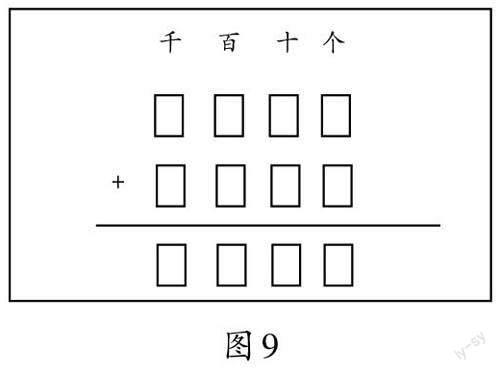
[學生總結出豎式模型（如圖9）]

（學生認為只有第一個豎式是正確的）

師（追問）：第二個和第三個豎式分別錯在哪里？

生（齊）：第二個豎式錯在相同數位沒有對齊，第三個豎式錯在沒有看清加減號。

【評析】通過練習鞏固計算方法，有助于提升學生的計算能力。學生總結出豎式模型，說明學生會用“模型意識和模型觀念”這樣的數學思維表述多位數加減法豎式，會用數學語言表達與交流。

四、回顧反思，總結提升

師：這節課接近尾聲了，你有哪些收獲？

生1：我學會了三位數加減兩、三位數的筆算。

生2：列豎式計算時，相同數位對齊，從個位算起。

生3：我學會了和小組內的同學合作學習。

生4：我學會了轉化和數形結合的思想。

……

【評析】《義務教育數學課程標準（2022年版）》指出，要讓學生經歷數學表達、概括歸納等學習過程，樹立學好數學的信心，養成良好的學習習慣。本環節引領學生從多方面回顧梳理，幫助學生總結基本的數學活動經驗，使學生在獲得數學知識的同時，加深對數學思想方法的理解。

［ 參 考 文 獻 ］

[1] 王玉鵬.小學數學教學使用益智器具的意義、問題和策略[J].教師教育論壇，2022，35（12）：55-57.

[2] 崔梅云，侯春蘭.基于核心素養的小學數學計算教學探究[J].求知導刊，2022（8）：50-52.

[3] 陳鋒，周煉.從學科素養導向看核心能力建構：《義務教育數學課程標準》有關“問題提出”的變化研究[J].中學數學月刊，2023（1）：4-6，11.

（責編 覃小慧）