小學數學智慧課堂與GeoGebra深度融合的案例分析

梁仕杰 江曉欣

摘? 要：文章主要通過三個小學數學的幾何教學案例來說明GeoGebra軟件在小學數學教學中的重要作用。其中，在滲透和了解“不完全歸納法”這一數學思想的幾何課型中，教師應用GeoGebra軟件，不僅能很好地體現出信息技術與學科的深度融合，還能構建出數字化的智慧課堂。使用GeoGebra軟件進行教學，能讓學生的學習更加高效、直觀和有趣，體現出學生的智慧學習和深度學習。

關鍵詞：GeoGebra;智慧課堂;深度學習;不完全歸納法

隨著科技的發展，信息技術已經影響著人們生活的方方面面。教育部在《義務教育數學課程標準（2022年版）》中明確指出：合理利用現代信息技術，提供豐富的學習資源，設計生動的教學活動，促進數學教學方式方法的變革。在實際問題解決中，創設合理的信息化學習環境，提升學生的探究熱情，開闊學生的視野，激發學生的想象力，提高學生的信息素養。因此，在如今的數學學習中以及信息技術與數學學科融合的前提下，教師和學生的“教”與“學”的方式也在不斷改變，平板電腦、VR眼鏡、可穿戴電子設備都出現在數學學習活動中。這些技術的出現，為學習者提供了更自主的學習方式、更多的學習資源和更廣的學習環境。但是，現在很多的平板課堂、VR課堂，并不是真正意義上的信息技術與學科深度融合的智慧課堂，或是深度學習的教學過程更多的是流于形式。因此，本研究會列出幾個GeoGebra軟件與小學教學幾何教學深度融合的智慧學習、深度學習的案例，以供參考。

一、小學數學中“不完全歸納法”與GeoGebra的深度融合

GeoGebra對比傳統的教學，它的優勢非常明顯，能為學生和教師提供直觀的幾何模型，真正做到思維可視化，并為學生提供了智慧學習和深度學習的條件。學生在小學數學中通過GeoGebra進行智慧學習，一般需要用“不完全歸納法”來得出相應的結論。

（一）GeoGebra幫助學生掌握三角形的內角和

很多教師都研究過“三角形內角和”這一經典課。該課是2014年人教版小學四年級數學下冊第五單元“三角形”的最后一個內容。在設計這節課時，教師應思考如何讓所有學生掌握任意三角形的內角和是180°，而不是讓學生被動接受這個結果。因此，教師可以利用GeoGebra設計“任意三角形的內角和”的課件（如圖1）。

在該課件中，學生可以對三角形進行任意位置的拖動，隨之，三角形的內角度數也會發生變化。通過計算，學生可以得到，無論拖動出來的三角形是什么類型，其內角和都是180°。在這里，教師會進行一次簡單的演繹推理：“同學們的三角形是通過自己隨意拖動，在沒有設定特定的條件下形成的，但大家的三角形的內角和都是180°，因此有理由認為，任意三角形的內角和都是180°。”

針對“內角和”這一經典課，大部分教師會設計“量算”和“撕拼”這樣的教學活動，但由于四年級學生是以直觀到抽象的思維過程為主，因此不能進行嚴格的演繹推理來證明本課的結論。而“量算”和“撕拼”都屬于驗證的范圍，實際操作是有誤差的，因此由大量的例子來得出結論就顯得尤為重要。而GeoGebra則能為學生提供大量的例子，讓學生不完全歸納出“三角形的內角和是180°”這一結論。

在整個探究的過程中，學生都是利用這個課件資源進行智慧學習的。如果學生愿意進行探究，得到的例子將非常多，并可以試圖利用這個課件資源去尋找一個反例反駁這一結論，而這個過程正是學生深度學習的過程。學生在探究的過程中，不僅獲得了“三角形的內角和是180°”這一結論，還對結論進行了質疑和反思，從而掌握了學習數學的方法，以及養成了反思的思維習慣。

（二）利用GeoGebra讓學生直觀感受“任意兩邊之差小于第三邊”

同樣是“三角形”這一單元的內容，對學生而言，“內角和”的課堂是比較有趣的，而三角形的三邊關系則是抽象性和邏輯性都很強。在教材的要求中，學生只要掌握三角形三邊關系中的一個即可，即“任意兩邊的和大于第三邊”，而不需要掌握另一個關系——“任意兩邊之差小于第三邊”。由于教材中沒有直觀的幾何模型讓學生理解這一關系，因此教材沒有安排這一內容。這時教師可以利用GeoGebra為學生制作出探究的課件，讓學生的學習內容更完整。

學生在學習“任意兩邊之和大于第三邊”這一關系時，教材事先安排學生學習了“兩點之間線段最短”這一公理，然后利用嚴格的演繹推理來說明“任意兩邊之和大于第三邊”。因此，教師在教授這一課時，也沒有用GeoGebra讓學生去驗證這個關系。而當學習完這一內容時，教師問學生：“既然三角形的任意兩邊和與第三邊有關系，那你還會聯想到什么內容？”大部分學生就會想，任意兩邊的差會跟第三邊有類似的關系嗎？正是這一個問題，引出了下一節課的教學方向。

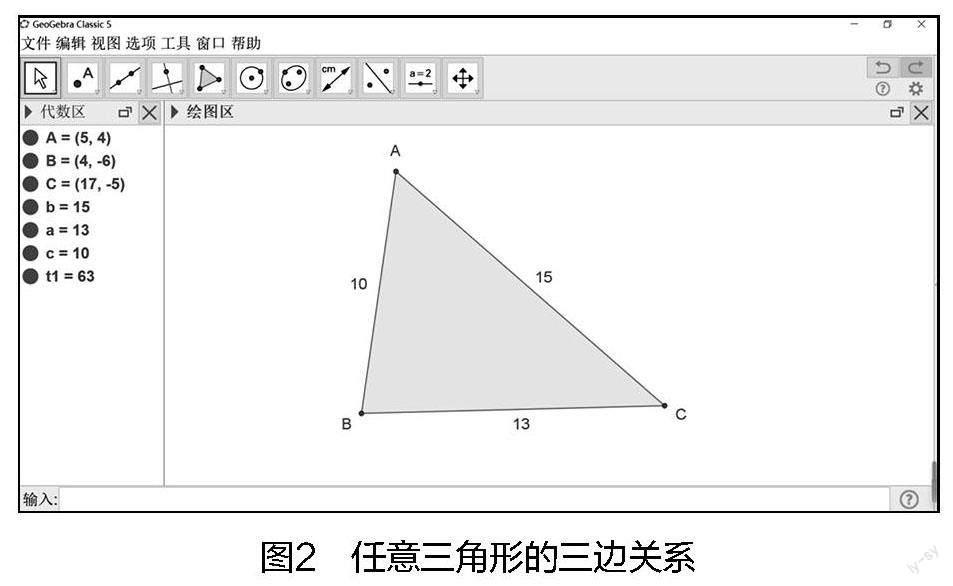
在教學“三角形任意兩邊之差小于第三邊”這一內容時，教師可以為學生提供以下的Geogebra課件和學習單（如圖2）。在該課件中，學生可以對三角形進行任意拖動，形成不同類型和不同大小的三角形，而對應的三角形的各邊的長度也隨之變化。學生記錄下每次拖動的三角形的數據，并在表格中進行計算和分析。

在整個探究過程中，學生利用了GeoGebra課件資源進行自主和個性化的探究和分析，最終得到結論。由于課堂時間只有40分鐘，留給學生探究的時間不多，因此學生可以在課后繼續分析。學生通過對各個例子的分析與不完全歸納，很容易就得到了“任意兩邊之差小于第三邊”的這一結論。

上述過程，已經體現了學生的智慧學習。同時在課堂上，有部分學生自覺地把上節課學習的“任意兩邊之和大于第三邊”和本節課得到的“任意兩邊之差小于第三邊”進行了對比和整合，最終得到了小學階段很少出現，而學生又可以理解的結論：三角形任意邊的取值范圍——兩邊差<第三邊<兩邊和。這是學生對獲得的新知和舊知進行對比和聯系，從而再獲得新知的過程，也正是本節課學生進行深度學習的一個體現。

（三）GeoGebra為學生直觀呈現正方體表面的涂色問題

在2021年人教版小學五年級數學下冊第三單元的“長方體和正方體”中，有這樣一個“探索圖形”的活動課。該課是讓學生探索這樣的一個問題：將n階正方體的表面涂上顏色，探究其三面涂色的小正方體個數、兩面涂色的小正方體個數、一面涂色的小正方體個數和沒有涂色的小正方體個數分別有幾個。

首先，這個問題在教材中的作用是，通過解決這個問題培養學生的數學思想;其次，培養學生能夠利用發現的規律解決問題。對這個問題，學生認為無從下手，教師也會認為很難在課堂上組織有效的教學。根本原因是，這是對立體圖形的探究，學生很難在腦海中直觀地想象，教師能提供的直觀的教具也有限（可能只有1階、2階、3階的正方體），難以讓學生進行有效的觀察并總結規律。為了解決上述問題，教師可以在堂課中為學生提供三種學習資源：一是由125個小正體堆積而成的大正方體，其中表面涂上了顏色，這一資源的應用是為了幫助空間想象能力比較弱的學生，在課堂上真正實現“做中研、做中學”;二是教師利用VR眼鏡，提供沉浸式的學習資源，讓學生戴上眼鏡觀察1至10階正方體的情況，最后總結出結論;三是教師利用GeoGebra的課件，提供一個可以改變階數、自由聚合與離散的正方體，讓學生進行探究。

根據學生的上課情況來看，這三種資源都有學生使用，但大部分學生都會選擇在平板電腦上使用GeoGebra課件進行探究，原因是學生認為這樣的課件比實物的小正方體更方便，相對于VR眼鏡，不用轉換場景，不會打斷學習的過程。下面是提供給學生的GeoGebra課件。

可以看到，正方體為聚合狀態時，其表面涂了顏色的情況（如圖3）;當正方體處于離散狀態時，正方體表面涂色和內部涂色的情況（如圖4）。由于這個課件可以自由旋轉，學生在實際操作中，可以任意觀看正方體上下左右前后的涂色情況，從而能直觀觀察出各種涂色的小正方體處在大正方體中的位置。這樣不僅能為學生直觀展示小正方體的情況，還能為學生進一步探索規律、形成數學思維提供有效的素材。

二、教學反思

本節課對學生而言，難點在于難以想象、難以觀察和難以描述。而教師利用GeoGebra課件，則可以幫助空間想象能力較弱的學生直接觀察，方便學生準確地描述發現。同時在該課中，學生不僅使用GeoGebra課件進行了探究學習，還在這樣的探究活動中，具有了以下的數學思維：一是用化繁為簡的方法進行數學問題的探究;二是對數學信息進行不完全歸納，得出結論;三是用字母表示最終的發現，以便實際運用。學生在對問題的探究中，有所發現和總結，并能得出結論和解決實際問題，這正是這堂課學生的智慧學習和深度學習的體現。

對這堂課，有點遺憾的是，學生未能完全使用GeoGebra課件進行更深入的探究。該課件除了能顯示各階數正方體的涂色情況外，還能調整正方體長寬高的參數，讓本節課的結論得到更多的結果。

在本研究原來的設想中，是讓學生將自己的發現聯系起來，得到下面的等式：

（n-2）3=n3-6n2+12n-8

但這個二項展開式已經超出小學生的認知水平，因此課堂的最后并沒有再延伸下去，但這為學生以后學習這方面的內容提供了一個很好的幾何直觀模型。

三、結語

通過上面的幾個課例可以看出，小學的幾何教學可以用Geogebra提供的資源讓學生進行學習，但不是所有的幾何教學都能用上。例如，上面提到的“三角形任意兩邊之和大于第三邊”這一堂課就無法使用，原因是課本提供了線段公理給學生，學生已經可以進行嚴格的演繹，推理得出結論，這時如果再使用GeoGebra來進行“不完全歸納”，就顯得思維層次較低。在小學教學中，關于呈現幾何動態過程的內容，教師也可以使用GeoGebra進行教學，如平行四邊形的面積、圓面積、圓柱體積等課型，都可以使用這個軟件。

本課例是對GeoGebra與小學數學教學深度融合的一次初步嘗試，希望通過本研究的論述，能為各數學教育工作者提供一些啟示和幫助。

參考文獻：

[1]李凱. 《義務教育數學課程標準（2022年版）》中課程實施的新變化[J]. 中學數學月刊，2023（04）：8-11.

[2]單慧. GeoGebra軟件在小學數學教學中的應用[D]. 蘇州：蘇州大學，2017.

[3]周瑤. GeoGebra輔助小學數學教學的實踐策略研究[J]. 考試周刊，2020（87）：68-69.

（責任編輯：鄒宇銘）