指向高階思維的一類概率背景遞推數(shù)列問題研究
——從2023年新高考Ⅰ卷第21題談起*
張長貴
(江蘇省無錫市輔仁高級中學(xué) 214123)
謝廣喜
(江南大學(xué)理學(xué)院 214122)
1 問題提出
數(shù)學(xué)是思維的科學(xué),“數(shù)學(xué)在形成人的理性思維、科學(xué)精神和促進(jìn)個人智力發(fā)展的過程中發(fā)揮著不可替代的作用”[1]1.培養(yǎng)學(xué)生的數(shù)學(xué)思維也成為數(shù)學(xué)教育研究的重要目標(biāo).高階思維最初是在美國教育學(xué)家布盧姆(B.S.Bloom)的教育目標(biāo)分類學(xué)的基礎(chǔ)上發(fā)展起來的.隨著新時代國家對人才培養(yǎng)質(zhì)量的新要求,傳統(tǒng)的用于學(xué)習(xí)事實性知識或完成簡單任務(wù)的思維能力,在布盧姆教學(xué)目標(biāo)分類中表現(xiàn)為較低水平的能力,如記憶力、淺表層次的理解力和近遷移的應(yīng)用能力等,已經(jīng)不能夠適應(yīng)對人的思維能力的要求.
所謂高階思維,是指解決劣構(gòu)問題的能力、遠(yuǎn)遷移能力和發(fā)散性思維能力[2].而問題、任務(wù)則是促進(jìn)學(xué)習(xí)者高階思維能力的核心[3].因此在教學(xué)中,教師要對高階思維的特點有一定認(rèn)識,需要為學(xué)生提供合適的問題,給學(xué)習(xí)者創(chuàng)設(shè)真實的、有挑戰(zhàn)性的復(fù)雜任務(wù),以便促進(jìn)學(xué)習(xí)者有效發(fā)展高階思維.
2 試題分析
2.1 以復(fù)雜情境為背景,考查問題解決能力
問題求解是一種包括回憶和組合相關(guān)規(guī)則以形成某種新的、更為復(fù)雜的規(guī)則的智力技能[2].高考數(shù)學(xué)試題重點考查學(xué)生的思維過程、實踐能力和創(chuàng)新意識,問題情境的設(shè)計應(yīng)自然、合理[1]88.2023年新高考Ⅰ卷第21題是一道基于概率背景的遞推數(shù)列綜合問題.此類問題的深層次思考可以聯(lián)系到高等數(shù)學(xué)中“隨機(jī)過程”的馬爾科夫鏈,而實際上問題突破的關(guān)鍵是全概率公式的運用.下面我們簡要分析一下這道試題,并介紹與之密切相關(guān)的問題.通過分析可以發(fā)現(xiàn),其實這道高考壓軸試題來源于教材例題和習(xí)題的組合及改造.所以高三教師在深入研讀高中數(shù)學(xué)教材(最好能將蘇教版與人教版結(jié)合起來研讀)的基礎(chǔ)上,應(yīng)為學(xué)生創(chuàng)設(shè)更復(fù)雜的新情境,避免試題指向簡單回顧、再現(xiàn)形式所反映的思維,要讓學(xué)生在問題解決的實踐中形成認(rèn)知策略,發(fā)展高階思維能力,這是應(yīng)考的必要捷徑與方略.
試題(2023年新高考Ⅰ卷第21題)甲、乙兩人投籃,每次由其中一人投籃,規(guī)則如下:若命中則此人繼續(xù)投籃,若未命中則換為對方投籃.無論之前投籃情況如何,甲每次投籃的命中率均為0.6,乙每次投籃的命中率均為0.8.由抽簽確定第1次投籃的人選,第1次投籃的人是甲、乙的概率各為0.5.
(1)求第2次投籃的人是乙的概率;
(2)求第i次投籃的人是甲的概率;
解析 (1)記“第i次投籃的人是甲”為事件Ai,“第i次投籃的人是乙”為事件Bi,所以有P(B2)=P(A1B2)+P(B1B2)=P(A1)P(B2|A1)+P(B1)P(B2|B1)=0.5×(1-0.6)+ 0.5×0.8=0.6.
類題聯(lián)想1(人教A版選擇性必修第三冊第91頁第10題)甲、乙、丙三人相互做傳球訓(xùn)練,第1次由甲將球傳出,每次傳球時,傳球者都等可能地將球傳給另外兩個人中的任何一人,求n次傳球后球在甲手中的概率.
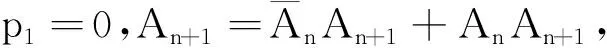
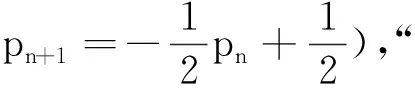
2.2 注重交叉學(xué)科知識,實現(xiàn)遠(yuǎn)遷移能力
學(xué)生高階思維的表現(xiàn)的主要特征包含“應(yīng)用整合多方信息、觀點或知識”“進(jìn)行評判和調(diào)整”[5].華東師范大學(xué)鐘啟泉教授也指出:“發(fā)展高階思維,要以高階學(xué)習(xí)活動予以支持.要以學(xué)習(xí)者為中心,要開展問題求解的學(xué)習(xí)活動……同時還應(yīng)該注重交叉學(xué)科知識的學(xué)習(xí).”[6]相對復(fù)雜的認(rèn)知情境“既需要學(xué)生綜合多學(xué)科知識來理解,也需要學(xué)生深入分析把握情境要素,還需要學(xué)生能夠?qū)η榫承畔⑷未嬲妗⒎直媸欠?以此來鍛煉學(xué)生的復(fù)雜思維能力”[7].因此具有交叉學(xué)科綜合背景的試題應(yīng)成為高階思維發(fā)生的重要場域,以此實現(xiàn)學(xué)習(xí)能力向表面特征、結(jié)構(gòu)特征不相似情境的遠(yuǎn)遷移.
類題聯(lián)想2(2023年浙江省杭州市高三模擬試題)馬爾科夫鏈?zhǔn)歉怕式y(tǒng)計中的一個重要模型,也是機(jī)器學(xué)習(xí)和人工智能的基石,在強化學(xué)習(xí)、自然語言處理、金融領(lǐng)域、天氣預(yù)測等方面都有著極其廣泛的應(yīng)用.其數(shù)學(xué)定義為:假設(shè)我們的序列狀態(tài)是…,Xt-2,Xt-1,Xt,Xt+1,…,那么Xt+1時刻的狀態(tài)的條件概率僅依賴前一狀態(tài)Xt,即P(Xt+1|…,Xt-2,Xt-1,Xt)=P(Xt+1|Xt).
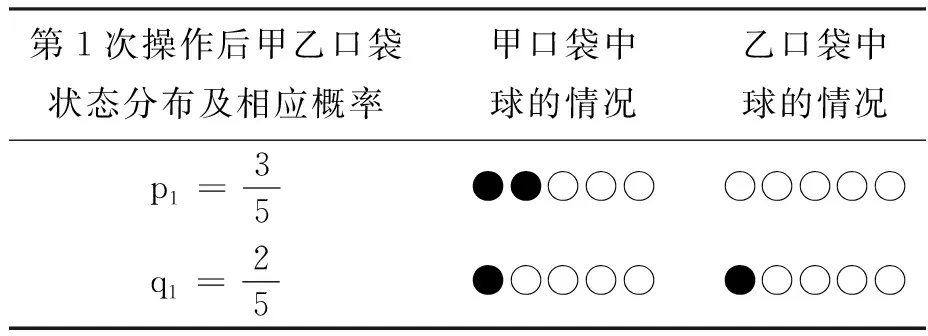
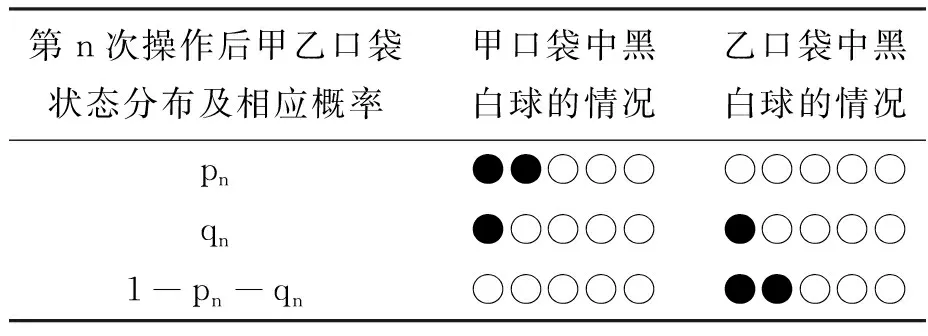
現(xiàn)實生活中也存在著許多馬爾科夫鏈,例如著名的賭徒模型:假如一名賭徒進(jìn)入賭場參與一個賭博游戲,每一局賭徒賭贏的概率為50%,且每局賭贏可以贏得1元,每一局賭徒賭輸?shù)母怕蕿?0%,且賭輸就要輸?shù)?元.賭徒會一直玩下去,直到遇到如下兩種情況才會結(jié)束賭博游戲:一種是手中賭金為0元,即賭徒輸光;一種是賭金達(dá)到預(yù)期的B元,賭徒停止賭博.記賭徒的本金為A(A∈N*,A 圖1 當(dāng)賭徒手中有n元(0≤n≤B,n∈N)時,最終輸光的概率為P(n),請回答下列問題: (1)請直接寫出P(0)與P(B)的數(shù)值; (2)證明{P(n)}是一個等差數(shù)列,并寫出公差d; (3)當(dāng)A=100時,分別計算B=200,B= 1 000時,P(A)的數(shù)值,并結(jié)合實際,解釋當(dāng)B→∞時,P(A)的統(tǒng)計含義. 解析 (1)當(dāng)n=0時,賭徒已經(jīng)輸光了,因此P(0)=1.當(dāng)n=B時,到了終止賭博的條件,不再賭了,因此輸光的概率P(B)=0. 美國心理學(xué)家吉爾福特指出,訓(xùn)練人的發(fā)散思維是培養(yǎng)創(chuàng)造力的一種方法.而決策、創(chuàng)造性思維則是高階思維能力的重要構(gòu)成.美國學(xué)者瑞尼克認(rèn)為:“高階認(rèn)知是一種復(fù)雜的、不規(guī)則的、能自我調(diào)節(jié),產(chǎn)生多種解決方法的認(rèn)知.”[8]這也說明了需要設(shè)置以發(fā)散的思維活動來揭示客觀事物本質(zhì)及內(nèi)在聯(lián)系的思維問題.比如選取概率中經(jīng)典的復(fù)雜模型問題,讓學(xué)生調(diào)用復(fù)雜思維(包含數(shù)學(xué)中的抽象、推理論證和數(shù)學(xué)建模)去參與問題解決,獲得自己對問題多方法、多角度的思考、理解和解釋,培養(yǎng)發(fā)散思維,從而產(chǎn)生創(chuàng)造性思維. 類題聯(lián)想3(2020年江蘇卷附加題改動)摸球模型是研究概率論問題的一種基本模型方法,現(xiàn)在甲口袋中裝有2個黑球和3個白球,乙口袋中裝有5個白球.現(xiàn)從甲、乙兩口袋中各任取一個球交換放入另一口袋,重復(fù)n次這樣的操作,記甲口袋中黑球個數(shù)為Xn,恰有2個黑球的概率為pn,恰有1個黑球的概率為qn. (1)求p1,q1和p2,q2; (2)試求數(shù)列{2pn+qn}的通項以及Xn的數(shù)學(xué)期望E(Xn)(用n表示). 解析 本題的難點在于每一次操作后甲乙系統(tǒng)所處的狀態(tài)的概率(pn,qn)依賴于前一次狀態(tài)的概率(pn-1,qn-1),然而系統(tǒng)前一次的狀態(tài)又有多種可能,所以需要我們以系統(tǒng)前一次狀態(tài)概率(pn-1,qn-1)為基準(zhǔn),建立其與系統(tǒng)當(dāng)前狀態(tài)的概率(pn,qn)之間的轉(zhuǎn)移遞推關(guān)系.注意到甲、乙兩個口袋中一共僅有2個黑球,故一般情況下黑球所在位置有三種可能(對應(yīng)系統(tǒng)的三種可能狀態(tài),因為黑球給定,白球自動確定,下面不再強調(diào)白球的數(shù)目):①甲袋里有2個黑球;②甲、乙兩個口袋里各有1個黑球;③乙袋里有2個黑球.具體研究如下: (1)(這一步算是送分題,但也不是十分容易,尤其是求p2和q2這一步) (ii)求(p2,q2),此時必須注意到,一般情形下,甲乙系統(tǒng)在每一次操作后都有三種可能的狀態(tài)(這一點非常重要,因為它為下一步問題的求解奠定必要的思想基礎(chǔ)).為了理解方便,我們形象地表示如下(必須指出:僅n=1時,才有pn+qn=1;當(dāng)n≥2時,pn+qn<1): 第1次操作后甲乙口袋狀態(tài)分布及相應(yīng)概率甲口袋中球的情況乙口袋中球的情況p1=35●●○○○○○○○○q1=25●○○○○●○○○○ (2)當(dāng)n≥2時,由題意可記第n次操作后狀態(tài)分布及相應(yīng)的概率如下表: 第n次操作后甲乙口袋狀態(tài)分布及相應(yīng)概率甲口袋中黑白球的情況乙口袋中黑白球的情況pn●●○○○○○○○○qn●○○○○●○○○○1-pn-qn○○○○○●●○○○ 根據(jù)此表,結(jié)合(pn+1,qn+1)的具體含義,容易得到 評注本題以概率論中經(jīng)典的波利亞(摸球)模型為載體,涉及了數(shù)學(xué)期望等基本的統(tǒng)計概念,具體考查了考生使用簡單的數(shù)列知識解決問題的能力.基于隨機(jī)變量的一段時間上的多個事件整體上形成隨機(jī)過程,這道題本質(zhì)上是一道隨機(jī)過程背景問題.這類當(dāng)前狀態(tài)的概率僅與上一次狀態(tài)的具體概率有關(guān)而與之前其他狀態(tài)的概率無關(guān)的隨機(jī)過程情形稱為馬爾科夫過程.它是隨機(jī)過程問題中的一種最重要的情形.在解決問題過程中,學(xué)生需要能夠發(fā)現(xiàn)思維發(fā)散的點:特殊的部分(p1,q1和p2,q2)與一般的整體(pn,qn)和(pn+1,qn+1)的關(guān)聯(lián)、分析(圖表法)與綜合(遞推關(guān)系)、邏輯演繹等,提升發(fā)現(xiàn)問題的能力、解決難題的能力,不斷發(fā)展創(chuàng)新思維能力. 高階思維能力是可以培養(yǎng)的,“核心素養(yǎng)、高階思維的培養(yǎng)必須以數(shù)學(xué)知識內(nèi)容為載體,在教學(xué)中我們要深刻理解教學(xué)內(nèi)容,挖掘其中蘊含的高階思維培育素材”.[9]因此比較有效的方法是將內(nèi)容、問題、教學(xué)進(jìn)行整合,讓學(xué)生投入到需要運用高階思維的高階學(xué)習(xí)中.教學(xué)中可以以一類問題的研究為主題,設(shè)置復(fù)雜的真實情境,引發(fā)學(xué)生分析、評價、創(chuàng)造的認(rèn)知思維過程,通過問題解決外顯學(xué)生的思維;通過解決跨知識領(lǐng)域的真實問題,訓(xùn)練學(xué)生從知識、經(jīng)驗的近遷移過渡到方法、思維的遠(yuǎn)遷移;還需通過對一些經(jīng)典復(fù)雜問題的分析和解決,培養(yǎng)學(xué)生的發(fā)散性思維.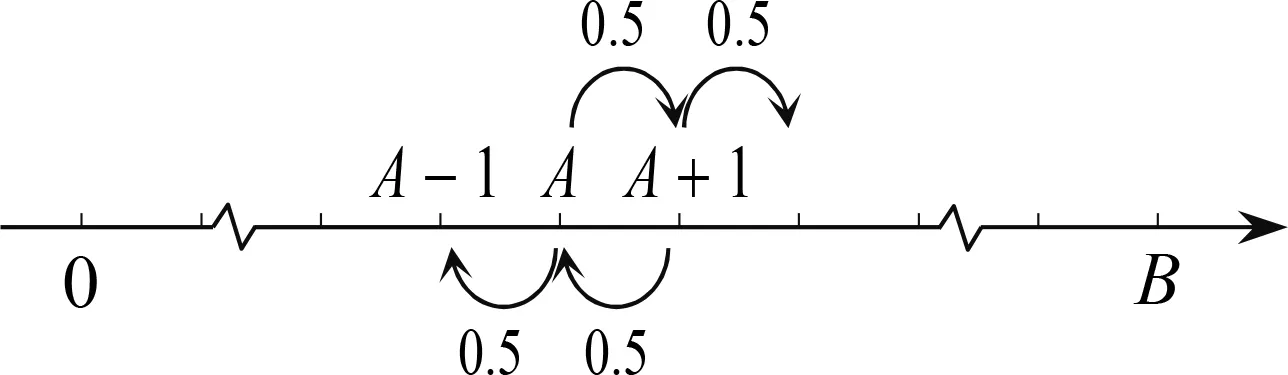
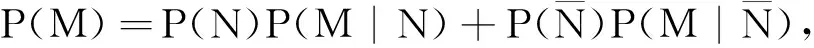
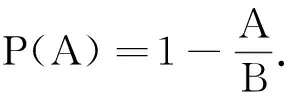
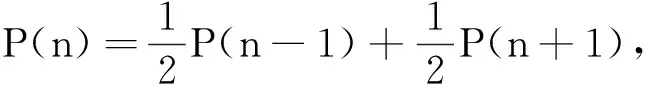
2.3 以經(jīng)典模型為問題,培養(yǎng)發(fā)散思維能力
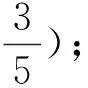
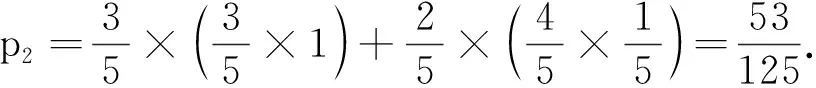
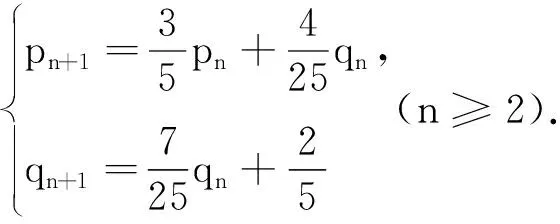
3 結(jié)語

