基于微分進(jìn)化算法的無(wú)線傳感器網(wǎng)絡(luò)覆蓋優(yōu)化問(wèn)題研究

坎 香 ，方 偉

1.江陰職業(yè)技術(shù)學(xué)院 計(jì)算機(jī)科學(xué)系， 江蘇 江陰 214405；2.江南大學(xué) 物聯(lián)網(wǎng)工程學(xué)院， 江蘇 無(wú)錫 214122

無(wú)線傳感器網(wǎng)絡(luò)（wireless sensor networks，WSN）涉及傳感器技術(shù)、無(wú)線通信技術(shù)、嵌入式技術(shù)、分布式信息處理技術(shù)等多個(gè)學(xué)科領(lǐng)域的內(nèi)容，是當(dāng)今學(xué)術(shù)研究的熱點(diǎn)領(lǐng)域之一［1-3］。WSN中的傳感器節(jié)點(diǎn)采用無(wú)線連接，以多跳自組織方式形成網(wǎng)絡(luò)，將感知信息傳送至匯聚節(jié)點(diǎn)，再由匯聚節(jié)點(diǎn)通過(guò)衛(wèi)星或物聯(lián)網(wǎng)發(fā)送至終端的任務(wù)管理節(jié)點(diǎn)進(jìn)行統(tǒng)一分析管理。WSN 的覆蓋方法是WSN 的一項(xiàng)關(guān)鍵基本技術(shù)，該方法的優(yōu)劣關(guān)系到組網(wǎng)成本和網(wǎng)絡(luò)容錯(cuò)能力，以及整個(gè)網(wǎng)絡(luò)的工作效率。因此，WSN 的覆蓋優(yōu)化方法是國(guó)內(nèi)外專(zhuān)家學(xué)者的重點(diǎn)研究方向之一［4-6］。

近年來(lái)，群體智能算法由于出色的尋優(yōu)能力被廣泛應(yīng)用于WSN 的覆蓋優(yōu)化［7-9］。文獻(xiàn)［10-11］提出利用遺傳算法較強(qiáng)的全局搜索能力和并行搜索能力實(shí)現(xiàn)WSN 的覆蓋優(yōu)化，但受局部搜索能力的限制，算法在最優(yōu)解附近收斂速度慢，從而導(dǎo)致動(dòng)態(tài)節(jié)點(diǎn)選擇的實(shí)時(shí)性不高；文獻(xiàn)［12］以最大化節(jié)點(diǎn)間的距離為適應(yīng)度函數(shù)，將微粒群算法應(yīng)用于WSN 的覆蓋問(wèn)題，實(shí)現(xiàn)以簇頭節(jié)點(diǎn)為中心向外均勻分布的節(jié)點(diǎn)部署形式，但該算法未考慮邊界約束問(wèn)題。

微分進(jìn)化算法是Rainer Storn 和Kenneth Price在1995年為求解切比雪夫多項(xiàng)式而提出，主要特點(diǎn)是收斂速度快、可調(diào)參數(shù)少、魯棒性好、算法簡(jiǎn)單，其基本思想在于利用當(dāng)前種群不同個(gè)體之間的差異，通過(guò)重組得到中間種群，并在子代與父代中選擇較優(yōu)個(gè)體來(lái)獲得新一代種群。作為一種新穎的進(jìn)化算法，微分進(jìn)化算法在面對(duì)非線性、不可微、多目標(biāo)、多約束的復(fù)雜優(yōu)化問(wèn)題時(shí)顯示出高效的尋優(yōu)能力，目前已成功應(yīng)用于攝像機(jī)標(biāo)定、生物信息學(xué)、工業(yè)生產(chǎn)優(yōu)化、變電站規(guī)劃、電力系統(tǒng)調(diào)度等領(lǐng)域。

目前微分進(jìn)化算法在WSN 路由算法上的應(yīng)用較多，但在WSN 覆蓋部署問(wèn)題上的應(yīng)用尚少。本文針對(duì)微分進(jìn)化算法在WSN 覆蓋問(wèn)題上的應(yīng)用特點(diǎn)，嘗試完善覆蓋模型、改進(jìn)算法的適應(yīng)度評(píng)價(jià)函數(shù)和選擇機(jī)制，以實(shí)驗(yàn)論證微分進(jìn)化算法在WSN覆蓋問(wèn)題上的可行性。

1 無(wú)線傳感器網(wǎng)絡(luò)覆蓋模型及改進(jìn)

1.1 基本覆蓋模型

設(shè)WSN 的監(jiān)測(cè)區(qū)域A 為L(zhǎng)×W的二維長(zhǎng)方形平面，將監(jiān)測(cè)區(qū)域A劃分為m×n個(gè)網(wǎng)格點(diǎn)，并布置N個(gè)傳感器節(jié)點(diǎn)。傳感器節(jié)點(diǎn)的集合為C={c1，c2，…，cN}，其中ci={xi，yi，r}（(xi，yi)為節(jié)點(diǎn)ci的位置坐標(biāo)，r為節(jié)點(diǎn)ci的傳感半徑），i=1，2，...，N。

本文采用二元感知模型，將節(jié)點(diǎn)的感知范圍等效成一個(gè)以節(jié)點(diǎn)位置為圓心、傳感半徑r為半徑的圓。網(wǎng)格點(diǎn)（x，y）是否被傳感器所覆蓋，可用式（1）進(jìn)行判斷，即

式中：Pcov(x，y，ci)為感知概率，i=1，2，...，N。

在監(jiān)測(cè)區(qū)域A 內(nèi)m×n個(gè)網(wǎng)格點(diǎn)中，只要存在一個(gè)網(wǎng)格點(diǎn)（x，y），使得Pcov(x，y，ci) = 1，即認(rèn)為該網(wǎng)格點(diǎn)（x，y）被傳感器節(jié)點(diǎn)ci所覆蓋。統(tǒng)計(jì)監(jiān)測(cè)區(qū)域A內(nèi)被覆蓋的總網(wǎng)格點(diǎn)數(shù)，再由式（2）計(jì)算WSN在監(jiān)測(cè)區(qū)域A內(nèi)的覆蓋率，即

式中：f為監(jiān)測(cè)區(qū)域A內(nèi)的覆蓋率，D為A內(nèi)被覆蓋的總網(wǎng)格點(diǎn)數(shù)。

1.2 覆蓋模型的改進(jìn)

1.2.1 傳感器圓心范圍的約束處理

在對(duì)監(jiān)測(cè)區(qū)域A 內(nèi)的L×W二維平面使用微分進(jìn)化算法進(jìn)行變異交叉過(guò)程中，可能會(huì)出現(xiàn)圓心落在區(qū)域外的節(jié)點(diǎn)，從而減小了節(jié)點(diǎn)的覆蓋面積。為此，需要將圓心落至監(jiān)測(cè)區(qū)域外的節(jié)點(diǎn)通過(guò)移動(dòng)的方式移動(dòng)至監(jiān)測(cè)區(qū)域內(nèi)，具體操作方式如下：

式中：x、y分別表示監(jiān)測(cè)區(qū)域內(nèi)任一傳感器節(jié)點(diǎn)的橫坐標(biāo)與縱坐標(biāo)；L、W分別表示監(jiān)測(cè)區(qū)域的長(zhǎng)和寬，m。

1.2.2 節(jié)點(diǎn)過(guò)于聚集的處理

為了提高WSN 的覆蓋率，在傳感器節(jié)點(diǎn)部署過(guò)程中，很可能出現(xiàn)傳感器節(jié)點(diǎn)過(guò)于聚集導(dǎo)致節(jié)點(diǎn)重疊的情況。為限制各覆蓋區(qū)域內(nèi)重疊節(jié)點(diǎn)的數(shù)量，減少節(jié)點(diǎn)的重疊區(qū)域，需要根據(jù)傳感器節(jié)點(diǎn)ci的位置，計(jì)算周邊的重疊節(jié)點(diǎn)數(shù)O(xi，yi)，公式如式（4）所示，即

式中：xj、yj分別表示監(jiān)測(cè)區(qū)域A內(nèi)傳感器節(jié)點(diǎn)cj的橫坐標(biāo)與縱坐標(biāo)，j=1，2，...，N。

令M是與監(jiān)測(cè)區(qū)域A的面積及傳感器節(jié)點(diǎn)個(gè)數(shù)N有關(guān)的常數(shù)，當(dāng)O(xi，yi)＞M時(shí)，節(jié)點(diǎn)ci的位置需要重新在覆蓋區(qū)域內(nèi)隨機(jī)生成。

2 基于改進(jìn)微分進(jìn)化算法的無(wú)線傳感器覆蓋優(yōu)化方法

2.1 基本微分進(jìn)化算法

微分進(jìn)化算法與遺傳算法相似，都含有變異、交叉和選擇幾個(gè)步驟，但相對(duì)于遺傳算法又具有參數(shù)少的優(yōu)點(diǎn)。

2.1.1 變異

微分進(jìn)化算法的變異操作是在種群中隨機(jī)選擇兩個(gè)個(gè)體作差分運(yùn)算，然后將所得向量差加權(quán)后，根據(jù)一定的規(guī)則加到第三個(gè)個(gè)體（基向量）上。這種變異方式有效利用群體中個(gè)體間的分布差異，增強(qiáng)了全局搜索性能。

在微分進(jìn)化中常用的變異算子有5 種，本文采用DE/rand/1的方式，即在傳感器分布時(shí)從群體中隨機(jī)選擇2 個(gè)個(gè)體Xr(t)、Xs(t)，以及種群中的最優(yōu)個(gè)體Xbest(t)，按照式（5）產(chǎn)生新的個(gè)體，即

式中：Xr(t) -Xs(t)為2個(gè)個(gè)體的向量差；F為縮放因子。

2.1.2 交叉

變異中差分運(yùn)算是微分進(jìn)化算法的關(guān)鍵。在變異操作完成后微分進(jìn)化算法采用均勻交叉的方法產(chǎn)生一些試驗(yàn)向量，以增加種群的多樣性。具體地說(shuō)，在無(wú)線傳感器網(wǎng)絡(luò)覆蓋中，監(jiān)測(cè)區(qū)域是個(gè)二維平面，種群中第i個(gè)個(gè)體的位置坐標(biāo)Xi=(Xi，1，Xi，2)（Xi，1表示第i個(gè)個(gè)體的第1 維分量，Xi，2表示第i個(gè)個(gè)體的第2 維分量）；對(duì)種群中第i個(gè)個(gè)體的每個(gè)分量Xi，k（k=1，2），隨機(jī)生成一個(gè)0～1之間的實(shí)數(shù)b，將經(jīng)過(guò)變異操作得到的中間個(gè)體Ui(t+ 1)和當(dāng)前進(jìn)化個(gè)體Xi(t)進(jìn)行雜交操作，得到候選個(gè)體Vi(t+ 1)，其中第k維分量的操作如式（6）所示，即

式中：交叉因子R∈[0，1]；z是針對(duì)第i個(gè)個(gè)體生成的一個(gè)屬于［1，2］且均勻分布的隨機(jī)整數(shù)。

這種交叉策略使得Vi，k(t+ 1)至少取到一個(gè)Ui，k(t+ 1)的值，即候選個(gè)體Vi(t+ 1)至少繼承一維中間個(gè)體Ui(t+ 1)的分量，以確保每個(gè)個(gè)體都有交叉，從而更有效地提高種群的多樣性，保證個(gè)體的進(jìn)化，防止陷入局部最優(yōu)。

2.1.3 選擇

為了保證算法收斂，基本微分進(jìn)化算法依照貪婪準(zhǔn)則進(jìn)行選擇操作，即將經(jīng)過(guò)變異、交叉后產(chǎn)生新個(gè)體的適應(yīng)度值與父代個(gè)體的適應(yīng)度值作比較，讓適應(yīng)度值好的個(gè)體進(jìn)入下一代。因此，在無(wú)線傳感器網(wǎng)絡(luò)覆蓋問(wèn)題中，通常將區(qū)域覆蓋率f作為微分進(jìn)化算法的適應(yīng)度函數(shù)。選擇操作如式（7）所示，即

式中：f(t)為第t代種群的覆蓋率，Ct為第t代種群集合。

通常區(qū)域覆蓋率越大，種群的覆蓋能力越強(qiáng)，就更可能被選入下一代中。

2.2 改進(jìn)的微分進(jìn)化算法

為提高微分進(jìn)化算法應(yīng)用于WSN 覆蓋問(wèn)題上的收斂速度和尋優(yōu)能力，本文針對(duì)微分進(jìn)化算法中的選擇操作，提出一種改進(jìn)的選擇優(yōu)化機(jī)制，具體流程如圖1所示。

圖1 基于改進(jìn)微分進(jìn)化算法WSN覆蓋優(yōu)化方法流程圖Fig. 1 Flow chart of WSN coverage optimization method based on improved differential evolution algorithm

在微分進(jìn)化算法中，如何選擇最優(yōu)個(gè)體進(jìn)入下一次迭代是個(gè)十分重要的問(wèn)題。在原微分進(jìn)化算法中，最優(yōu)個(gè)體的選擇采用“優(yōu)勝劣汰”的淘汰機(jī)制，即將變異后的子代個(gè)體與原父代個(gè)體進(jìn)行對(duì)比，如果比父代更適合生存，那么用子代個(gè)體取代父代個(gè)體，否則仍采用父代個(gè)體。這種算法的特點(diǎn)是收斂速度較慢。

為提高算法的收斂速率，新的群體選擇不再采用原來(lái)的單個(gè)個(gè)體的優(yōu)勝劣汰，而是在原父代Ct與變異后子代群體Ct+1中選出最優(yōu)的H個(gè)個(gè)體作為新的種群，并進(jìn)入下一次迭代過(guò)程。在新的選擇操作中，采用單個(gè)節(jié)點(diǎn)的覆蓋率（即單個(gè)節(jié)點(diǎn)的覆蓋率對(duì)總覆蓋率有無(wú)提升）對(duì)個(gè)體進(jìn)行適應(yīng)度評(píng)價(jià)，從而在保證個(gè)體變異隨機(jī)性的同時(shí)加大了上一代優(yōu)異因子留下來(lái)的可能性。

按照?qǐng)D1的流程，覆蓋優(yōu)化方法步驟如下：

（1） 明確問(wèn)題定義域，輸入WSN 監(jiān)測(cè)區(qū)域、傳感器節(jié)點(diǎn)以及改進(jìn)微分進(jìn)化算法的相關(guān)參數(shù)。

（2） 初始化H個(gè)個(gè)體的坐標(biāo)，即在問(wèn)題定義域中隨機(jī)產(chǎn)生H個(gè)傳感器節(jié)點(diǎn)的原始位置，創(chuàng)建初始種群，初始化交叉因子、縮放因子等環(huán)境參數(shù)。

（3） 按式（5）計(jì)算傳感器群體中各個(gè)節(jié)點(diǎn)經(jīng)過(guò)變異操作后的坐標(biāo)。

（4） 將經(jīng)過(guò)變異后各節(jié)點(diǎn)的中間個(gè)體坐標(biāo)按式（6）計(jì)算傳感器群體中各個(gè)節(jié)點(diǎn)經(jīng)過(guò)交叉操作后的坐標(biāo)。

（5） 判斷傳感器群體中各個(gè)節(jié)點(diǎn)圓心是否落在監(jiān)測(cè)區(qū)域外。針對(duì)落在監(jiān)測(cè)區(qū)域外的節(jié)點(diǎn)，按式（3）對(duì)這些節(jié)點(diǎn)的坐標(biāo)進(jìn)行重新計(jì)算，使得這些節(jié)點(diǎn)移動(dòng)至監(jiān)測(cè)區(qū)域內(nèi)，以對(duì)其進(jìn)行圓心范圍的約束處理。

（6） 根據(jù)傳感器群體中每個(gè)節(jié)點(diǎn)ci的坐標(biāo)位置，按式（4）計(jì)算周邊的重疊節(jié)點(diǎn)數(shù)O(xi，yi)；當(dāng)O(xi，yi)＞M時(shí)，將節(jié)點(diǎn)ci的位置重新在覆蓋區(qū)域內(nèi)隨機(jī)生成。

（7） 對(duì)經(jīng)過(guò)上述步驟產(chǎn)生的候選傳感器節(jié)點(diǎn)群體中的每個(gè)節(jié)點(diǎn)，采用每個(gè)節(jié)點(diǎn)的覆蓋率對(duì)每個(gè)節(jié)點(diǎn)進(jìn)行適應(yīng)度評(píng)價(jià)；然后從候選傳感器節(jié)點(diǎn)群體和當(dāng)前傳感器節(jié)點(diǎn)群體中選出H個(gè)適應(yīng)度值（節(jié)點(diǎn)覆蓋率）最大的節(jié)點(diǎn)，作為新的傳感器群體中的節(jié)點(diǎn)。

（8） 判斷當(dāng)前傳感器節(jié)點(diǎn)群體的覆蓋率是否達(dá)到預(yù)先設(shè)定的值或者當(dāng)前算法的迭代次數(shù)是否達(dá)到最大迭代次數(shù)。若滿足，則算法結(jié)束，輸出最優(yōu)解即為傳感器群體中最優(yōu)的節(jié)點(diǎn)；否則，返回步驟（3），繼續(xù)進(jìn)行下一次迭代。

3 仿真實(shí)驗(yàn)及分析

假設(shè)仿真實(shí)驗(yàn)需要覆蓋的傳感區(qū)域?yàn)?00 m×100 m，種群規(guī)模H=40，即有40 個(gè)相同配置的無(wú)線傳感器，每個(gè)傳感器的傳感半徑r=12 m，最大迭代次數(shù)d=200，縮放因子F=0.7，交叉因子R=0.5。仿真實(shí)驗(yàn)在MATLAB 環(huán)境下進(jìn)行，每個(gè)實(shí)驗(yàn)都隨機(jī)進(jìn)行30次，并記錄平均覆蓋率。

3.1 傳感器圓心范圍的約束處理對(duì)覆蓋率的影響

采用基本微分進(jìn)化算法，比較覆蓋優(yōu)化模型在傳感器圓心范圍約束處理前后的影響，結(jié)果如圖2 所示。從圖2 可以看出，覆蓋優(yōu)化模型加入范圍約束后，隨著迭代次數(shù)的增加，迭代曲線更加平緩，平均覆蓋率從82.67%上升到89.87%。說(shuō)明圓心范圍的約束措施是有效的。

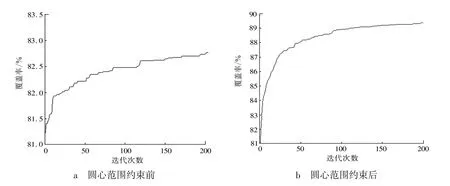
圖2 覆蓋率收斂曲線Fig. 2 Coverage convergence curve

3.2 重疊節(jié)點(diǎn)的處理對(duì)覆蓋率的影響

采用基本微分進(jìn)化算法，比較覆蓋優(yōu)化模型在處理重疊節(jié)點(diǎn)前后的覆蓋能力，結(jié)果如圖3 所示。由圖3 可以看出，覆蓋優(yōu)化模型引入重疊節(jié)點(diǎn)的處理之后，隨著迭代次數(shù)的增加，迭代曲線更加平緩，平均覆蓋率從81.79% 上升到89.68%。說(shuō)明節(jié)點(diǎn)的重疊處理措施是有效的。

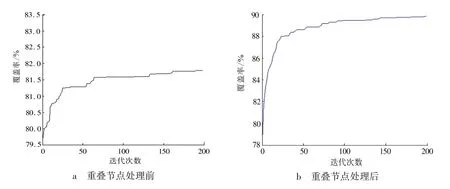
圖3 覆蓋率收斂曲線Fig. 3 Coverage convergence curve

3.3 不同微分進(jìn)化算法對(duì)覆蓋率的影響

利用改進(jìn)的覆蓋模型，采用基本微分進(jìn)化算法與改進(jìn)微分進(jìn)化算法綜合比較算法的平均覆蓋率，結(jié)果如圖4 所示。由圖4 的收斂曲線可見(jiàn)，相比基本微分進(jìn)化算法，隨著迭代次數(shù)的增加，改進(jìn)的微分進(jìn)化算法迭代曲線更加平緩，平均覆蓋率從81.40%上升到89.53%。

圖4 覆蓋率收斂曲線Fig. 4 Coverage convergence curve

3.4 改進(jìn)覆蓋模型及改進(jìn)微分進(jìn)化算法對(duì)覆蓋率的影響

采用改進(jìn)的覆蓋模型和改進(jìn)的微分進(jìn)化算法進(jìn)行仿真，結(jié)果如圖5 所示。由圖5 可見(jiàn)，在優(yōu)化過(guò)程的第一代時(shí)，群體的平均覆蓋率僅為78.91%；到了第50 代的時(shí)候，群體的平均覆蓋率達(dá)到了88.80%；到了第150 代時(shí)，平均覆蓋率已達(dá)到89.72%。說(shuō)明隨著進(jìn)化代數(shù)的增加，覆蓋率逐步上升，即采用的傳感器圓心范圍約束及重疊節(jié)點(diǎn)處理的措施是有效的，能夠提高無(wú)線傳感器的網(wǎng)絡(luò)覆蓋范圍。

圖5 基于改進(jìn)微分進(jìn)化算法及改進(jìn)覆蓋模型的覆蓋率收斂曲線Fig. 5 Convergence curve of coverage based on improved differential evolution algorithm and improved coverage model

4 結(jié)論

通過(guò)將微分進(jìn)化算法應(yīng)用于無(wú)線傳感器分布優(yōu)化的研究，在對(duì)微分進(jìn)化算法的選擇操作進(jìn)行改進(jìn)后，發(fā)現(xiàn)在同等條件下，與基本微分進(jìn)化算法相比，改進(jìn)算法的性能及收斂性能都有了較大提升；改進(jìn)覆蓋優(yōu)化模型對(duì)無(wú)線傳感器網(wǎng)絡(luò)的覆蓋率也有明顯提高。因此，要改善算法的性能，提高網(wǎng)絡(luò)節(jié)點(diǎn)覆蓋率，應(yīng)對(duì)覆蓋模型進(jìn)行有效處理，并對(duì)基本微分進(jìn)化算法進(jìn)行一定的改進(jìn)。