基于改進NSGA-Ⅱ算法的醫療垃圾轉運站選址優化研究

郭政杰 孫 濤＊

（內蒙古科技大學信息工程學院，內蒙古 包頭 014010）

1 醫療垃圾轉運相關研究

醫療垃圾轉運站的選址是一種綜合決策問題。肖鴻等[1]設計出新穎的醫療垃圾的回收模式與流程，通過運用Lingo軟件進行計算，對回收的節點進行選址決策。類似的問題還有城市生活垃圾轉運站的選址問題。衡婷等[2]運用模糊德爾菲法，對城市生活垃圾分類轉運站的選址體系進行選擇并提出相應的建議。周浩等[3]為了解決交通線路建設物資的物流節點選址問題，建立以運輸成本和時間懲罰成本之和為目標函數的數學模型，在經典的P-median選址模型基礎上，采用線積分取代離散點表示現狀需求，證明目標函數在給定區間內為凸函數，利用二次插值和黃金分割法相結合的算法對模型進行求解。Kargar等[4]提出一種多目標線性規劃模型，最小化運輸處理醫療垃圾的費用、運輸風險以及存放在醫院未收集的醫療垃圾這三個目標。潘馬超等[5]為了促進垃圾分類政策的實施，科學、合理地在居民生活小區設置垃圾分類站，建立選址模型和成本模型對垃圾分類站建設運營成本及居民滿意度負效應成本進行求解，通過對比K-means聚類算法和Cmeans聚類算法驗證了K-menas聚類算法的優越性。Yao等[6]針對醫療垃圾的處置開發了一種雙層平衡優化模型，在減小醫療垃圾可能對公眾造成危害風險的同時，可以降低運輸和處理醫療垃圾的費用。Joneghani等[7]針對醫療廢物管理中的選址分配問題，提出了一種不確定性條件下的多目標混合整數線性規劃模型，此模型設計了一個網絡，為醫療廢棄物的儲存、凈化、回收、焚燒和處置提供方案。

2 基于保護弱勢群體的醫療垃圾轉運站選址模型

2.1 P-median選址模型

P-median選址問題是一個經典的設施選址問題[8]，研究如何選擇P個服務站使得需求點和服務站之間的距離與需求量的乘積之和最小。在本文的Pmedian模型中，服務站即醫療垃圾轉運站，需求點即為城市中的各個醫院。每個需求點的需求量即為每家醫院每日產生且需要轉運的醫療垃圾量。本模型中假設醫院之間以及醫院與醫療垃圾轉運站之間的距離均為直線距離。模型約束條件主要有兩類：一類是醫療垃圾轉運站與幼兒園、養老院以及污水處理廠等地址的最小距離約束；另一類是醫療垃圾轉運站與各個醫院的最大距離約束。

P-median模型的目標是使醫療垃圾轉運站與醫院之間的距離和各個醫院每日產生的醫療垃圾量的乘積之和最小，最小化醫療垃圾的轉運成本。模型構建公式為：

式中：Z——P-median模型目標函數；i——醫療垃圾轉運站；I——醫療垃圾轉運站集合；j——醫院；J——醫院集合；o——養老場所；O——養老場所集合；p——污水處理廠；P——污水處理廠集合；k——幼兒園；K——幼兒園集合；wij——i轉運站對j醫院的醫療垃圾轉運量（kg）；dij——i轉運站與j醫院之間的距離（km）；dio——醫療垃圾轉運站i與養老場所o的距離（km）；dip——醫療垃圾轉運站i與污水處理廠p之間的距離（km）；dik——醫療垃圾轉運站i到幼兒園k的安全緩沖距離；dh——醫療垃圾轉運站與敏感區域的安全距離，設為0.8 km；dz——醫療垃圾轉運站和醫院之間的最大距離，此處設為5 km；Xij——0～1變量，i服務于j則Xij為1，否則為0。

2.2 選址風險模型

醫療垃圾中存在很多傳染性的病毒和細菌，因此醫療垃圾轉運站周圍一定的半徑范圍內不能存在人員密集的場所或綠地、水系，應盡可能遠離這些場所。本研究中把這些場所稱為敏感地址。本模型假設醫療垃圾轉運站對周圍的危害風險主要集中在橫向的平面區域，不考慮縱向的危害風險。模型的約束條件為醫療垃圾轉運站與周圍敏感地址的距離約束，模型目標是在醫療垃圾轉運站服務區域內，最大化醫療垃圾轉運站與其周圍敏感地址的距離。模型構建公式為：

式中：S——醫療垃圾轉運站與人員密集場所以及水源、綠地等地址距離的目標函數；q——具體的人員密集場所以及水源、綠地等地址；Q——具體的人員密集場所以及水源、綠地等地址的集合；diq——醫療垃圾轉運站i與敏感地址q的距離（km）；dm——醫療垃圾轉運站與敏感地址的最大距離，此處設為5 km；Xiq——0～1變量，i方圓2 km內存在q則Xiq為1，否則為0。

2.3 多目標規劃模型

本模型是對P-median選址和選址風險兩個模型進行同步規劃，約束條件與以上兩個模型的約束條件相同。此模型旨在同時兼顧醫療垃圾轉運站的轉運成本最小化以及醫療垃圾轉運站對周邊敏感地址可能造成的危害風險最小化這兩個優化目標。

Multi Objective為P-median和選址風險模型的多目標規劃目標函數，多目標規劃模型公式為：

式中：dab——地球上任意兩點a與b之間平面距離；R——地球的半徑，6 371 km；na——a處緯度弧度；nb——b處緯度弧度；ma——a處經度弧度；mb——b處經度弧度；majd——a處經度；mbjd——b處經度；nawd——a處緯度；nbwd——b處緯度。

3 實驗的設計與實現

3.1 實驗數據說明

本文收集了包頭市72家大中型公立醫院的地理信息坐標數據和病床數，138家包頭市的主要幼兒園的地理信息坐標數據、50家包頭市養老院和養老公寓機構的地理信息坐標數據以及3家污水處理廠以及相關在建工程的地理信息坐標數據。預估72家醫院每日需要轉運的醫療垃圾量時，根據醫院的級別以及病床數來進行估算[9]，全國性的三甲醫院一般單位病床每日產生0.74 kg醫療垃圾，省級重點醫院一般單位病床每日產生0.6 kg醫療垃圾，地市級別的醫院一般單位病床每日產生0.48 kg醫療垃圾。

3.2 實驗流程

實驗流程分為三個步驟。第一步是對城市醫院進行K-means聚類計算實現區域劃分；第二步是運用Lingo軟件對P-median模型進行求解；第三步是運用改進后的NSGA-Ⅱ算法進行多目標規劃求解，實現多目標規劃模型目標函數值的最小化。

3.2.1 K-means聚類計算

（1）K值的設定。

本文采用K-means聚類算法對城市醫院進行初步聚類，將距離相近的醫院分為同一個類別，對不同的類別再次進行聚類計算，得出最終的細分區域的個數。細分區域的個數即為轉運站的個數，即每一個醫療垃圾轉運站負責特定的幾家醫院的醫療廢棄物的回收。因此，本實驗首先采用K-means聚類算法對包頭市72家主要的大中型公立醫院進行分類，運用聚類算法前需要初步確定聚類的個數，實驗采用“手肘法”得出最優的聚類個數為3，因此將72家醫院分為3個類別。其中“手肘法”的核心指標是誤差平方和（SSE），計算公式為：

式中：Ci——第i個簇；P——Ci中的樣本點；mi——Ci的質心（Ci中所有樣本的均值）；SSE——所有樣本的聚類誤差，代表了聚類的優劣。

隨著K增大，樣本劃分會更精細，每個簇的聚合程度會逐漸提高，SSE就會逐漸變小。K值增大到一定程度時，再增加K值得到的聚合程度回報會迅速變小，所以SSE的下降幅度會驟減。

“手肘法”實驗結果如圖1所示。

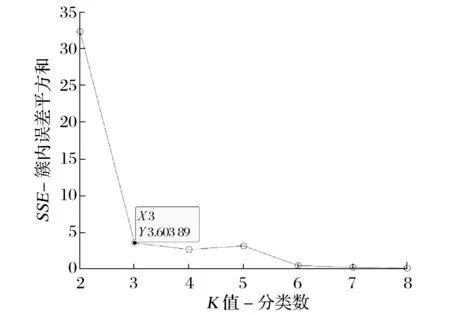
圖1 “手肘法”實驗結果

由圖1可知，當K≤3時，誤差平方和迅速減小；當K≥3時，誤差平方和曲線變得平緩，此時“手肘法”認為K=3是最優值。

（2）兩次聚類計算與分析。

確定k=3后，對醫院地理數據進行K-means聚類計算，完成聚類計算后，將72家醫院根據地理位置分為三個類別即A、B、C三個區域，由于每個區域內部醫院的分布密度有較大差異，因此分別對A、B、C三個區域再次進行K-means聚類分析實驗。此步驟實驗采用Matlab2021b中的數據聚類工具箱，求出各區域內部最優的分類個數。A區域聚類實驗結果如圖2所示。

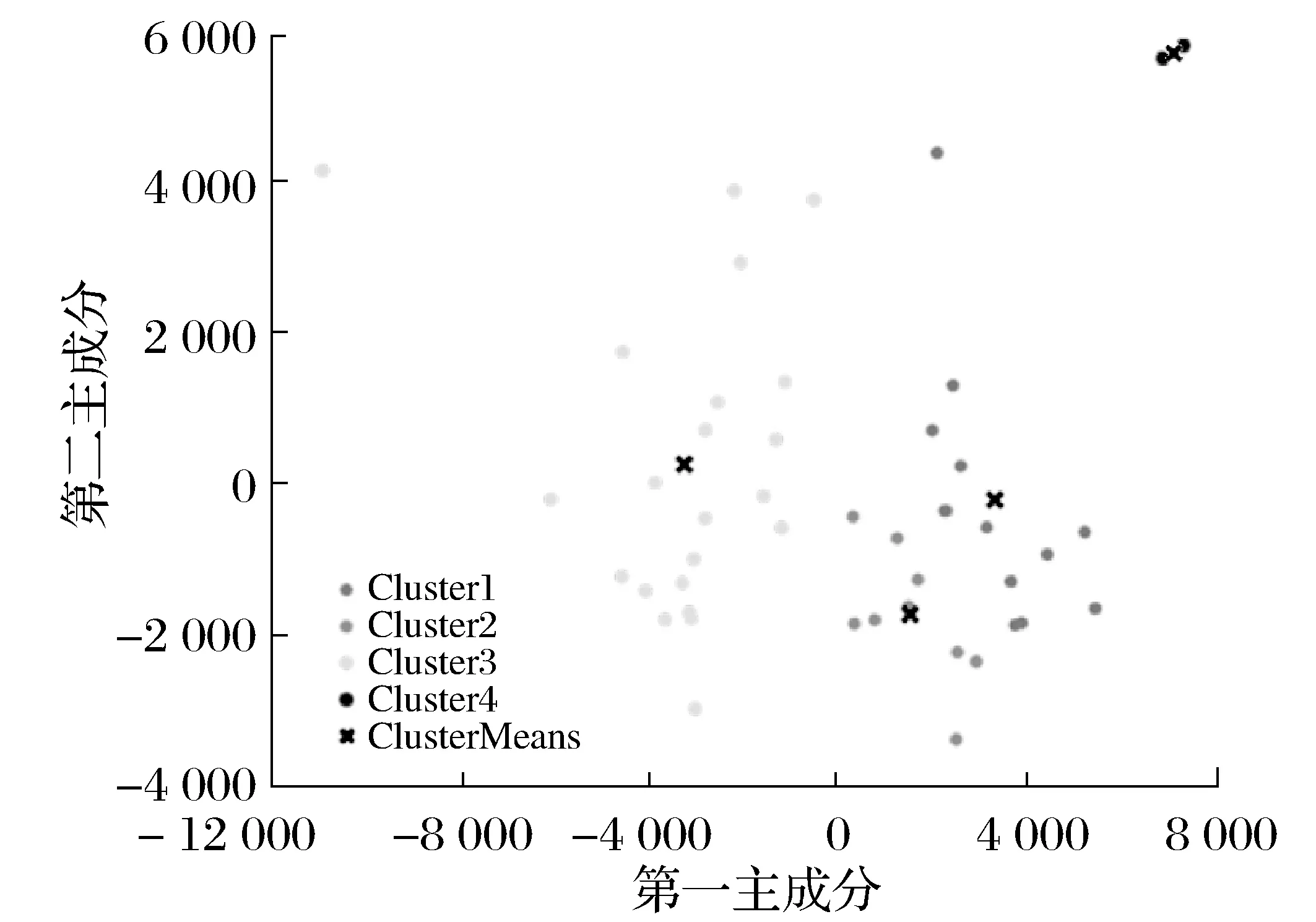
圖2 A區域K-means聚類分析實驗

A區域的最優分類數是4個，以此方法求出B區域的最優分類數是2個，C區域的最優分類數1個。因此，在A、B、C三個區域分別選擇4、2、1個醫療垃圾轉運站地址，其中，A區域的4個細分區域命名為A1、A2、A3、A4，B區域的2個細分區域命名為B1、B2，C區域的細分區域為C1。其中A1、A2、A3、A4區域分別包含18、2、21、5家醫院；B1、B2區域分別包含14、9家醫院；C1區域共包含3家醫院。

3.2.2 運用Lingo對A1區域P-中位模型求解

本文在進行多目標規劃之前，會先使用交互式的線性和通用優化求解器（Lingo）對各個細分區域進行P-median模型計算，計算出在本文P-median模型的約束條件下的最優解即潛在醫療垃圾轉運站的地理坐標。在此坐標周圍半徑2 km內，搜索出所有的人口密集場所和敏感地址的地理坐標，為下一步的選址風險模型做準備。以A1區域為例，A1區域包含18家醫院、27家幼兒園、7家養老院。通過Lingo對A1區域進行P-median模型計算，潛在選址經度109.791 5、緯度40.644 4，P-中位模型最小模板函數值13 482.95。設點（109.791 5，40.644 4）為潛在選址的坐標A1q，在A1q周圍半徑2 km內又搜索出6個人口密集場所和敏感地址。

由于A1區域有18家醫院和6個敏感地址，因此A1區域的多目標規劃模型需要同時優化24個目標，其中18個為P-median模型的優化目標，旨在使該區域醫療垃圾轉運站同每家醫院的距離與每家醫院每日需要轉運的醫療垃圾量的乘積之和最小。6個為選址風險的優化目標，旨在使該區域的醫療垃圾轉運站與6個敏感地址的距離之和最小。

地理位置坐標和名稱如表1所示。

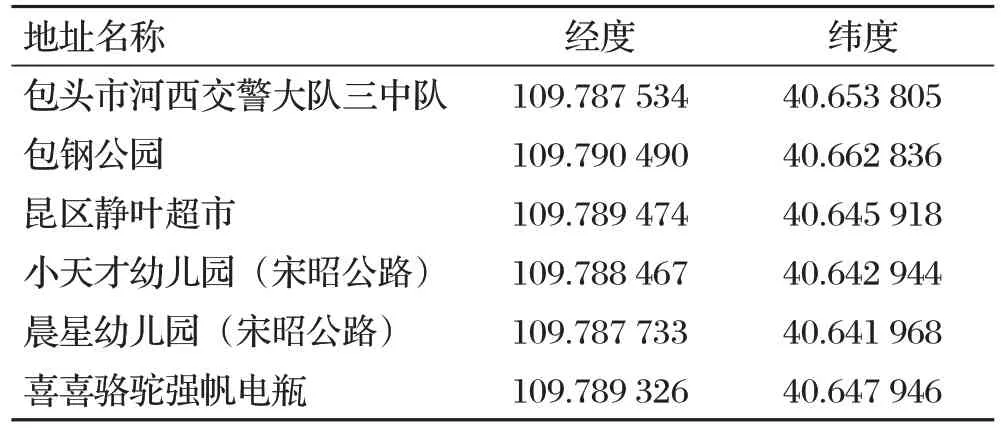
表1 A1q周圍2 km內敏感地址坐標

3.2.3 多目標規劃模型設計

傳統的NSGA-Ⅱ算法在初始化種群時采用隨機生成，隨機產生意味著不確定，因此在解決多目標非線性規劃問題時，容易陷入局部最優或者種群空間分配不均勻的問題。本實驗改進了傳統的NSGA-Ⅱ算法，采用傳統的NSGA-Ⅱ算法計算出多目標規劃函數的解集，從中挑選出目標函數值低的解；再次運行NSGA-Ⅱ算法，但在生成第一代子群時，不再隨機產生初始種群集合，而是采用第一步NSGA-Ⅱ算法計算并挑選出來的解集即“佳點”種群作為初始種群，然后進行計算求解。改進后的NSGA-Ⅱ算法如圖3所示。

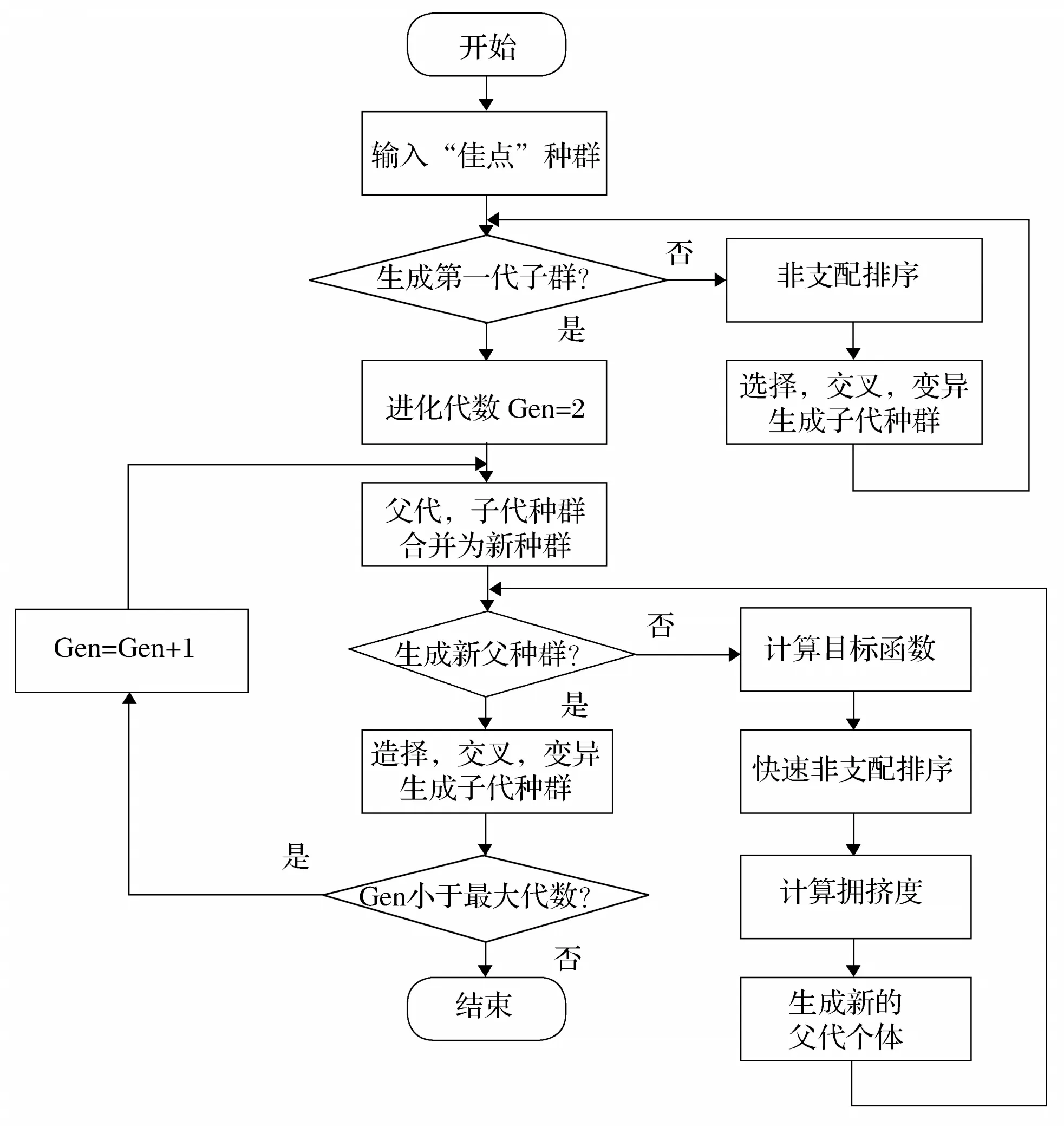
圖3 改進后的NSGA-Ⅱ算法流程

鑒于選址風險模型是以K-means聚類算法計算得出的每個細分區域為單獨的對象，對其進行風險模型計算，使各細分區域潛在的醫療垃圾轉運站的備選地址坐標與敏感地址的坐標在約束條件下保持盡可能遠的距離。本實驗中的選址風險模型包含于多目標規劃模型中，因此選址風險模型不再單獨論述。經過改進后的NSGA-Ⅱ算法計算出來的解集中的P-median模型的目標函數值和選址風險模型目標函數值均有降低，表明改進過的NSGA-Ⅱ算法求出的解集更優。改進前后的A1區域P-median目標函數值計算結果如圖4所示。

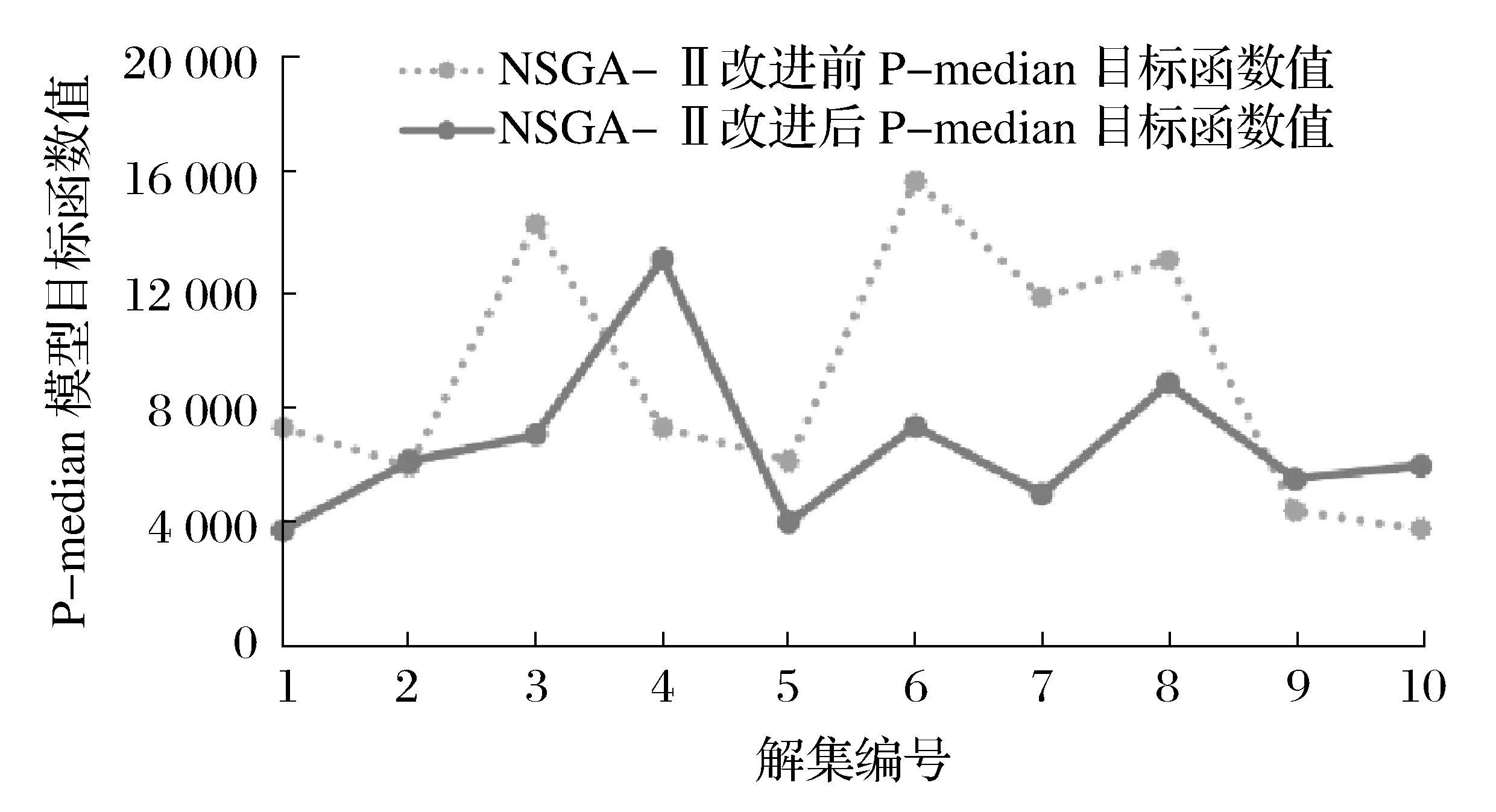
圖4 NSGA-Ⅱ改進前后P-median目標函數值對比

經過改進后的NSGA-Ⅱ算法計算出來的選址風險目標函數值也有明顯下降，結果如圖5所示。

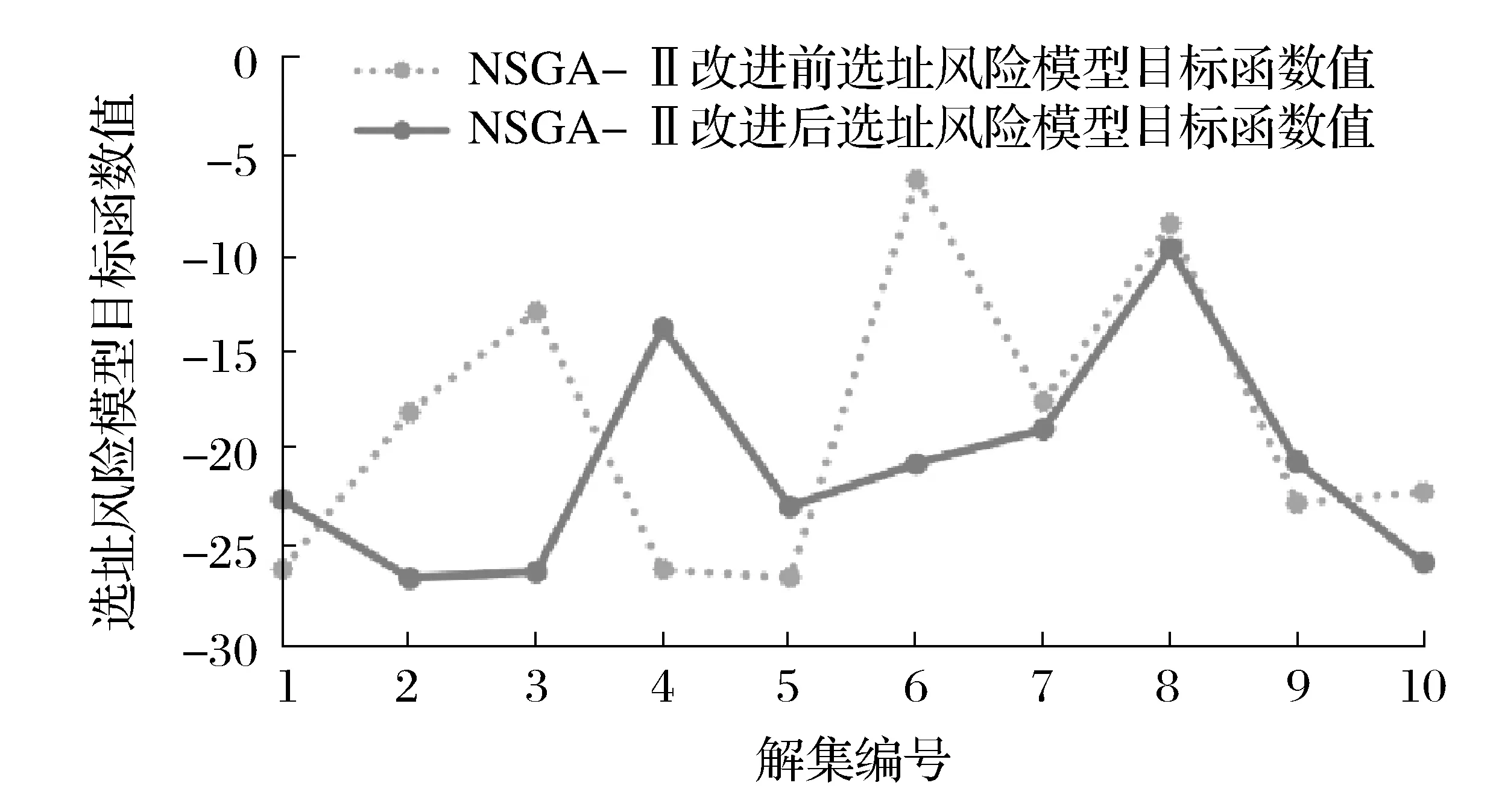
圖5 NSGA-Ⅱ改進前后選址風險模型目標函數值對比

通過改進NSGA-Ⅱ算法，本文中多目標規劃中的P-median模型和選址風險模型的目標函數值都取得了明顯的下降，其中P-median的目標函數值平均下降了11.44%，選址風險模型的目標函數值平均下降了33.39%。改進后的解集優于改進前的解集。

4 實驗結果評價

本文采用CRITIC權重法（客觀賦權法）對解集中的選址坐標進行賦權評價，最終選出最優的解，即選出區域內最優的醫療垃圾轉運站的地址坐標。

采用SPSSPRO在線數據分析軟件進行CRITIC權重法的計算與分析，SPSSPRO是一款集專業統計方法與數據算法于一體的在線式數據處理與分析平臺。本文對最終選址的評價設定了四個指標，分別為轉運站備選地址與交通干道的距離、轉運站備選地址與人口聚集區的距離、轉運站備選地址與醫療垃圾處理中心的距離、轉運站備選地址下風向居民點的數量。醫療垃圾處理中心在本文中指的是包頭市的醫療垃圾處置點包頭市綠源公司；醫療垃圾轉運站備選地址的下風向在本研究中假設是指東南風向。相關指標數據如表2所示。

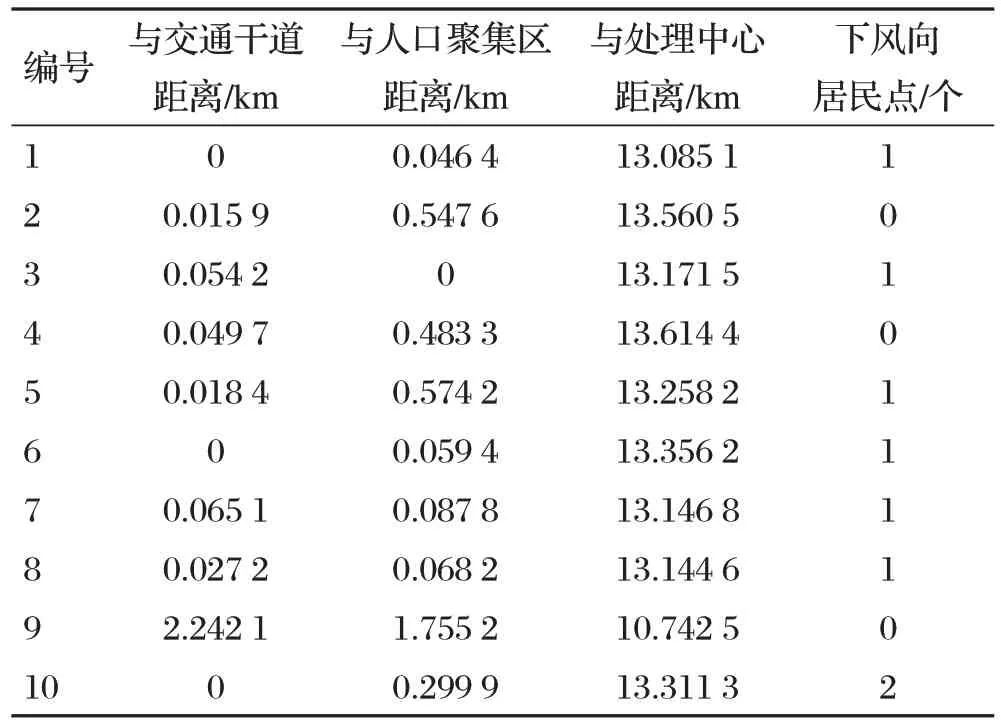
表2 A1區域備選地址評價數據

運用SPSSPRO在線數據分析軟件進行CRITIC權重法的計算與分析，分析過程中對醫療垃圾轉運站的備選地址與醫療垃圾處理中心的距離以及此備選地址下風向的居民點的數量，兩個指標進行負向化處理。指標負向化指的是值越大越劣，越小越優。備選地址下的居民點數量越少越優，備選地址距離醫療垃圾處理中心的距離越小越優。A1區域備選地址評價指數權重如表3所示。

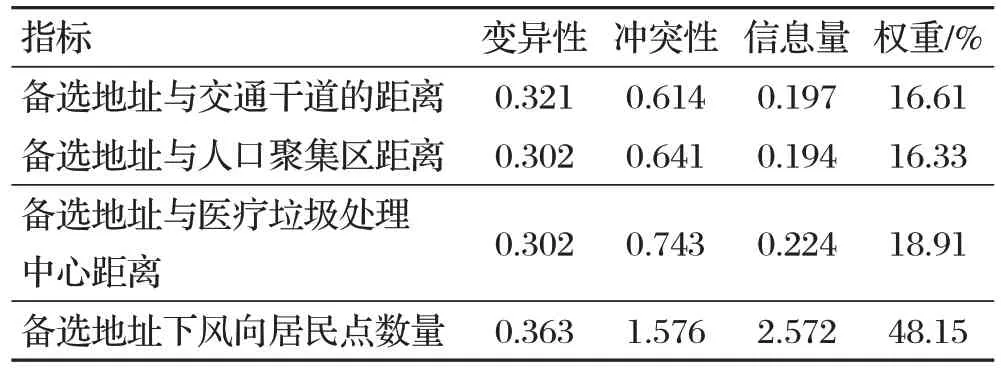
表3 A1區域備選地址評價指數權重

根據表3的權重計算備選地址的最終得分，編號1～10對應權分別為2.35、2.36、2.38、2.38、2.48、2.39、2.39、2.37、3.19、2.59。

第9號備選地址的得分值最高，為3.196 0，因此9號備選地址為A1區域最終的備選地址，地理坐標為（109.755 046，40.638 082），根據本文的研究思路和實驗方法及評價體系，求出所有區域最終的醫療垃圾中轉站的地址，結果如表4所示。

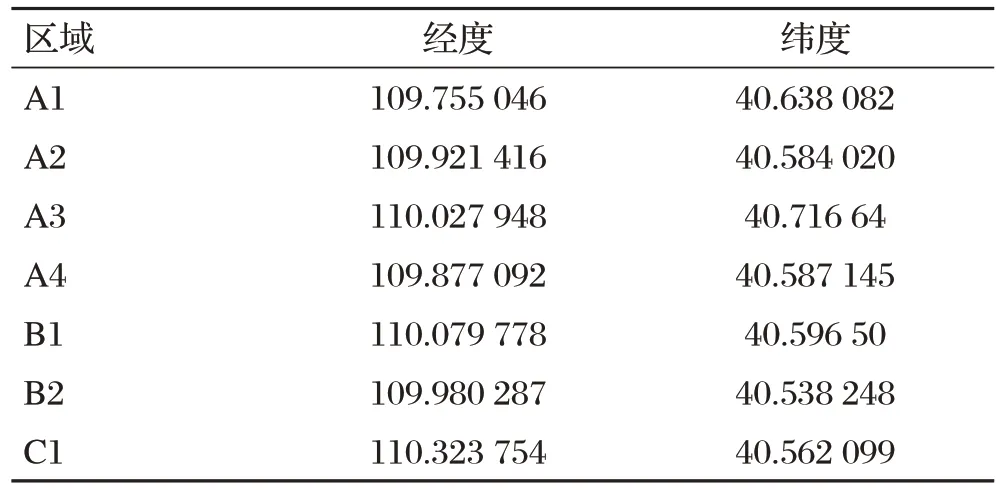
表4 所有區域醫療垃圾轉運站的最終選址坐標

5 結語

本研究在考慮對弱勢群體保護的基礎上，首先采用K-means聚類算法對城市的醫院進行分區，確定各個區域的醫療垃圾轉運站的數量，采用改進后的NSGA-Ⅱ算法對P-median模型和選址風險模型進行多目標規劃，降低了模型的目標函數值，降低醫療垃圾轉運站對周圍人口造成危害的風險，降低了醫療垃圾的轉運成本。最后采用CRITIC權重法對醫療垃圾轉運站的備選地址進行賦權計算，求出最優醫療垃圾轉運站選址的地理坐標。