基于值和左、右偏離度的模糊數排序

徐晨晨，葉國菊，劉 尉*，史芳芳，趙大方

（1.河海大學理學院,江蘇 南京 210098；2.湖北師范大學數學與統計學院,湖北 黃石 435002）

模糊集理論在許多研究領域都發揮著重大的作用，如決策、模糊信息的處理等。模糊環境下的風險分析，又稱模糊風險分析，越來越受到研究者的歡迎。文獻[1]首先在生產系統中引入了模糊風險分析，其中涉及的參數是發生故障的概率和損失的嚴重程度。不同時期的研究人員提出了各種解決風險分析的方法[2-6]，一般情況下，將這些風險分析問題所涉及的參數表示為語言術語，通常用模糊數來表示。這就需要對這些模糊數進行排序，以便更適當地進行決策。文獻研究[2-6]表明，隨著時代的發展，各種排序方法層出不窮。不幸的是，沒有公認的模糊數的排序方法。人們發現，現有的方法有時無法解釋模糊數的排序順序，因此，需要合乎邏輯的排序方法是極其重要的。許多研究者在模糊數的排序方面做出了巨大的貢獻，提出了越來越多有效的方法。自1976 年以來，已有30 多個模糊數的排序指標被提出[3-19]。

這里，本文對已有的一些排名方法進行簡單的回顧，不同的模糊數的排序方法是基于不同的概念和定義。Yager[7]采用了模糊數質心的概念。Wang 等[8]對質心公式進行了修正，提出了一種廣義的模糊數排序方法。但是文獻[8]中的方法無法區分具有面積補償的模糊數，因此，Yu 等[9]改進了文獻[8]中的方法。此外，該方法已被推廣用于不同類型的模糊數進行排序。Chen 等[10]提出了一種考慮正邊面積、負邊面積和廣義模糊數高度的方法。然而，當模糊數對稱且核相同時，該方法無法區分這些模糊數。Chen 等[11]又提出了一種考慮模糊數的高度和支撐，對不同高度和不同支撐的廣義模糊數排序的方法。然而，該方法無法區分具有面積補償的模糊數。文獻[12]提出了一種基于參考函數角度的模糊數排序方法。然而，具有精確值的模糊數不具有角度的概念；因此，該方法在這種情況下無法區分。Rezvani 等[13]提出了一種利用模糊數Mellin 變換得到的方差指數對梯形模糊數排序的方法。由于具有精確值的模糊數不存在方差，因此，該方法在這類模糊數中無法區分它們。Wang 等[8]首次提出了L-R 偏離度的思想，之后Asady[14]重新定義了L-R 偏離度，但是保留了Wang等[8]方法中的所有缺陷。因此，需要新的方法克服現有方法的這些局限性和缺點。最近，Cheng 等[16]使用了Yager[7]提出的黃金法則代表值的概念并對它進行了推廣，提出了一種新的模糊數排序方法。Barazandeh 等[17]利用模糊數的左、右高度不同，提出了一種對廣義模糊數進行排序的新方法。之后，Patra[18]借助廣義梯形模糊數的均值、面積和周長，提出了一種廣義梯形模糊數的排序方法。此外，在模糊數的排序指標中引入模糊數的值的計算公式能夠產生良好的結果，如Chutia 等[19]利用模糊數的值和模糊度的計算公式，對區間2 型模糊數進行了排序。但是當模糊數的值計算結果相等時，該方法就無法對這些模糊數和它們所對應的像進行正確的排序。

鑒于以上情況，本文提出了一種基于模糊數的值以及左、右偏離度的排序方法，并引入了一個參數λ來衡量排序指標是否包含偏離度。接著，利用模糊數和它們的像之間的各種關系，討論了所提出方法的自反性、反對稱性和傳遞性等性質，從而驗證了該方法的合理性。最后，通過數值例子與其他排序方法進行比較表明，該方法在所有情況下優于其他方法，克服了傳統的排序方法無法對某些模糊數排序的局限性。

1 預備知識

定義1[2]設 R是實數集。若A:R →[0,1]滿足以下條件：

1)A是正規的模糊集，即?x0∈R 使得A(x0)=1；

2)A是凸模糊集，即對任意的x＞y＞z，有A(y)≥A(x)∧A(z)；

3)A是上半連續函數，即對 ?x0∈R，?ε ＞0，?δ ＞0使得當 |x-x0|＜δ 時，有A(x)＜A(x0)+ε；

定義2[4]設A=(a,b,c,d;ω)∈E1是一個廣義的模糊數，其隸屬函數定義為

定義3[4]設A=(a,b,c,d;ω)∈E1是一個廣義的梯形模糊數，其隸屬函數定義為

其中，0 ≤ω ≤1。

如果 ω=1，則A=(a,b,c,d;1)是正規梯形模糊數。如果ω=1并且b=c，則是正規三角模糊數。

定義4[5]設A=(a,b,c,d;ω)∈E1，則稱-A=(-d,-c,-b,-a;ω) 是A的像。

定義5[6]設A=(a,b,c,d;ω)∈E1，s:[0,1]→[0,1]是關于y的函數，則A的值定義為

定義6[5]設Ai=(ai,bi,ci,di;ωi)，i=1,2,···,n，?1是非常小的正數，則Ai的傳遞系數定義為

定義7[4]設Ai=(ai,bi,ci,di;ωi)，i=1,2,···,n，則Ai關于amin和dmax的左、右偏離度定義為

2 主要結論

本節提出了一種利用值和左、右偏離度對模糊數排序的新方法，并給出了一些重要的引理和定理來驗證該方法的合理性。

定義8設Ai=(ai,bi,ci,di;ωi)，i=1,2,···,n，則Ai的排序指標定義為

其中，

定義9設Ai,Aj∈E1，定義以下序關系

引理 1設A=(a,b,c,d;ω)∈E1，則VA=-V-A。

證明：由式子(3)可知

證明：由定義 6 可知

將x代替為-y得，

證明：設Ai?Aj，則

由引理 1、引理 2 和引理3 可得

因此，可以分3 種情況討論。

定理 2設A，B，C是任意3 個模糊數，有以下結論成立：

1）A?A。(自反性)

2）A?B，B?C，則A?C。(傳遞性)

3）如果A?B，B?A，當且僅當A～B。(反對稱性)

證明：1）結論顯然。

2）設A?B，B?C，其中A，B排序指標中的參數λ 記為λ1，B，C排序指標中的參數 λ 記為λ2，證明可以分為以下4 種情況進行討論。

①當 λ1=λ2=0 時，DA≥DB且DB≥DC。因為λ1=λ2=0，所以VA≥VB，VB≥VC，VA≥VC。因此，DA≥DC，A?C。

②當 λ1=λ2=±1時，DA≥DB且DB≥DC。因為λ1=λ2=±1，所以VA=VB，VB=VC，可以得到

則有

因此，DA≥DC，A?C。

③當 λ1=±1，λ2=0時，DA≥DB且DB≥DC。因為λ1=±1，λ2=0，所以V(A)=V(B)，V(B)≠V(C)，可以得到V(B)≥V(C)，V(A)≥V(C)。因此，DA≥DC，A?C。

④當 λ1=0，λ2=±1時，DA≥DB且DB≥DC。因為λ1=0，λ2=±1，所以V(A)≠V(B)，V(B)=V(C)，可以得到V(A)≥V(B)，V(A)≥V(C)。因此，DA≥DC，A?C。

3）設A?B，B?A，則DA≥DB，DB≥DA。因此，DA=DB，A～B。

3 數值例子

例1：假設有一個正規模糊數A=(0.1,0.2,0.2,0.3;1.0)和一個非正規的模糊數B=(0.1,0.2,0.2,0.3;0.8)。很顯然，從人類的直覺角度來說，由于這兩個模糊數具有相同的支撐，并且B的高度為0.8，所以人們更認為A大于B。通過各種方法對這兩個模糊數進行排序，如表1。從表中可以看出文獻[7]、文獻[14]和文獻[15]的方法無法區分它們。文獻[8]、文獻[9]和文獻[13] 可以得到A?B，但是無法區分它們的像。而利用本文提出的方法，由于DA=0.200 0，DB=0.128 0以及根據定理1 可知，對這兩個模糊數及其像進行排序的順序分別為A?B，-A?-B，這是符合人類直覺的。此外，這與文獻[10]、文獻[11]和文獻[12]的結果一致。

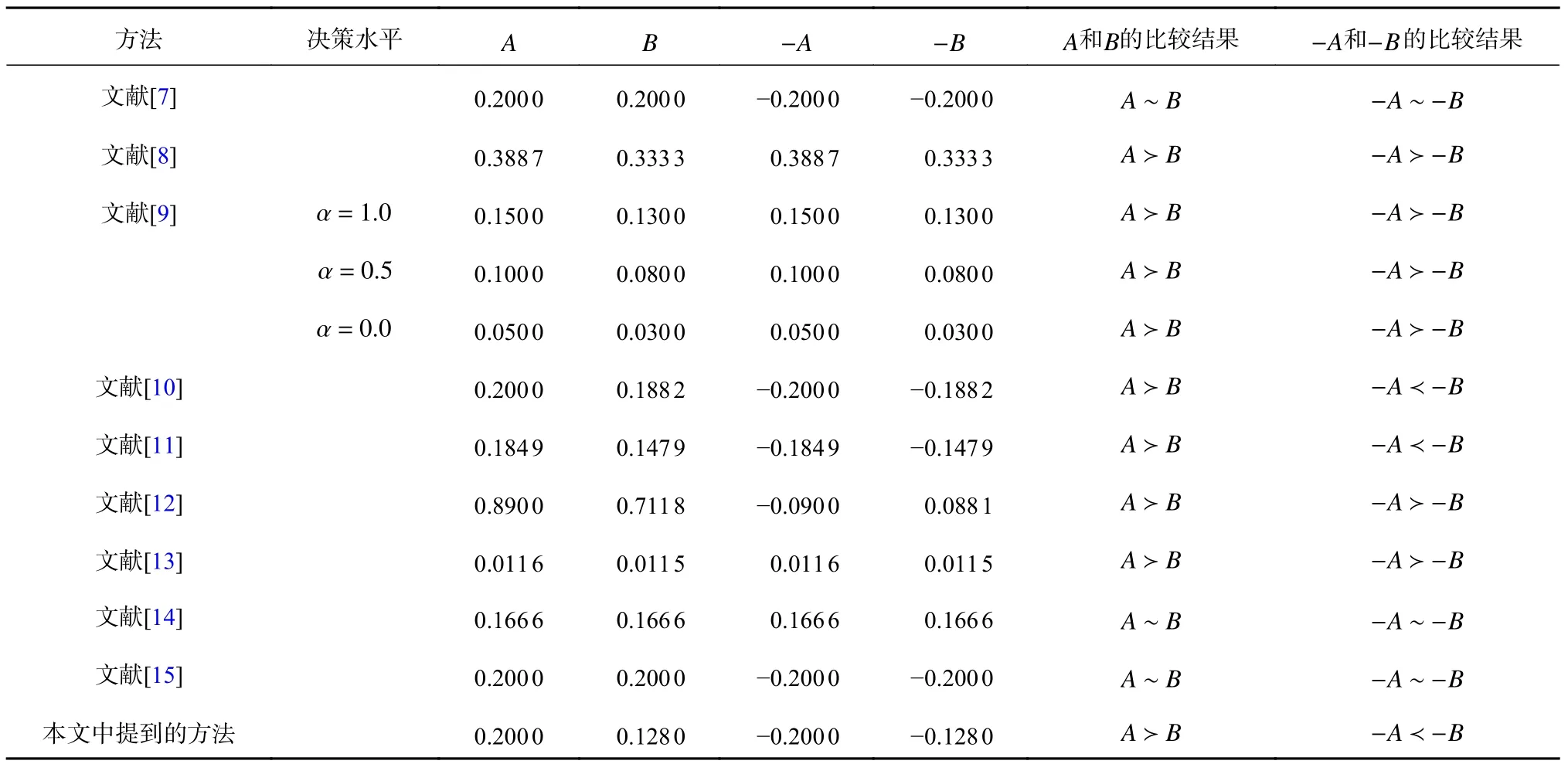
表1 例1 中的模糊數排序Tab.1 Ranking of fuzzy numbers in Example 1。

例2：假設有兩個具有面積補償的模糊數A=(0.1,0.4,0.4,0.5;1.0)和B=(0.2,0.3,0.3,0.6;1.0)，通過各種方法對兩個模糊數進行排序，如表2。從表中可以看出文獻[10]、文獻[11]和文獻[12]的方法無法區分它們。文獻[8]和文獻[13]可以得到A?B，但是無法區分它們的像。而利用本文提出的方法，由于DA=0.366 7，DB=1.6667以及根據定理 1 可知，對這兩個模糊數及其像進行排序的順序分別為A?B，-A?-B，這與文獻[7]和文獻[9]的結果一致。

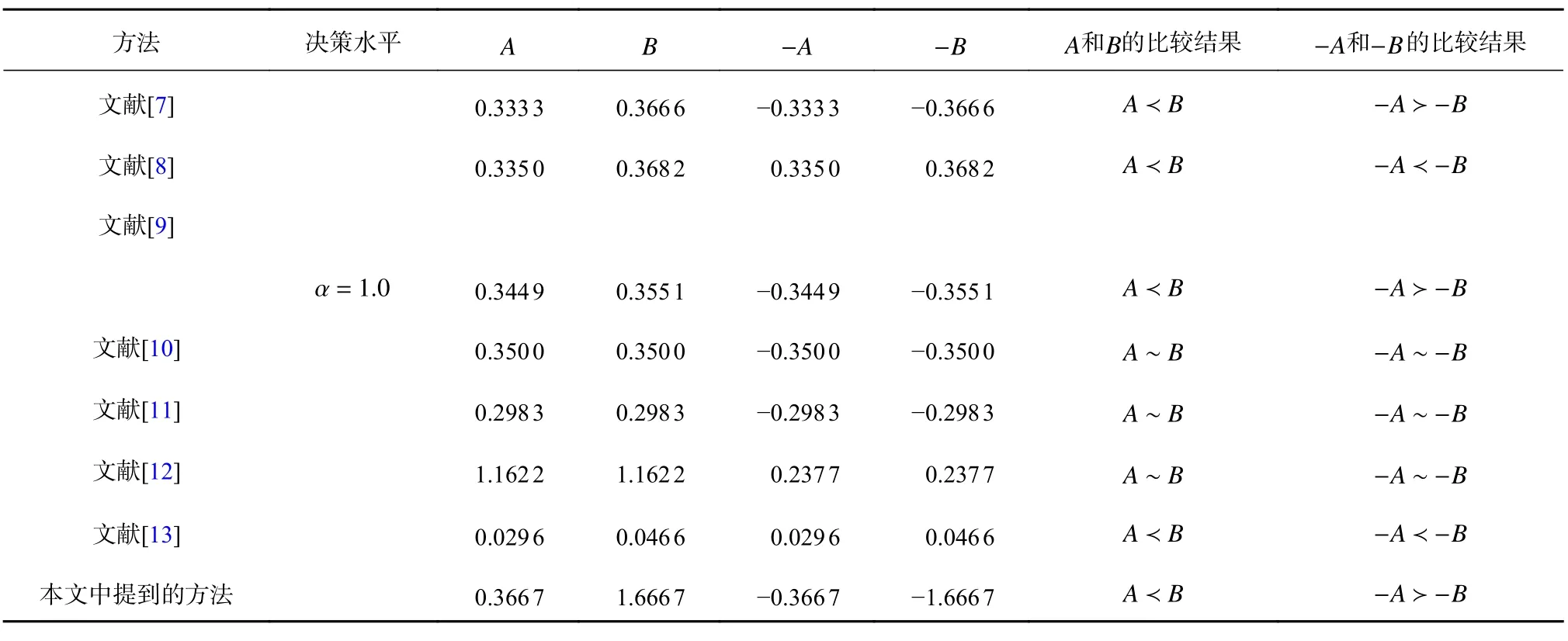
表2 例2 中的模糊數排序Tab.2 Ranking of fuzzy numbers in Example 2。

例3：假設模糊數A=(0.1,0.2,0.2,0.6;1.0)，B=(0.25,0.275,0.275,0.3;1.0)和C=(0.2,0.3,0.3,0.4;1.0)。通過各種方式對這3 個模糊數進行排序，如表3。文獻[7]和文獻[8]根據模糊數的質心進行推斷，當A和C的質心相等時，導致A和C之間的決策難以區分，這是一種錯誤的排序。此外，文獻[8]和[9]的方法表明圖像的排序與這些模糊數不一致。文獻[10]無法區分完全不同的模糊數A和B。雖然，[12]對這些模糊數進行了排序，但他們未能對其圖像進行排序。文獻[13]的排序準則只依賴于模糊數的方差。從模糊數來看，我們可以說A的方差大于C，C的方差大于B，因此得出B?C?A的結論是不正確的。因此，當模糊數具有相同的質心和不同的支撐時，這些方法無法做出正確的決策。然而利用本文提出的方法，由于DA=0.250 0，DB=0.275 0，DC=0.300 0以及定理1 可知，對這些模糊數及其圖像的排序分別為A?B?C，-A?-B?-C，這種方法得到的結果是更符合邏輯的并且與文獻[11]、[14]和[15]結果一致。

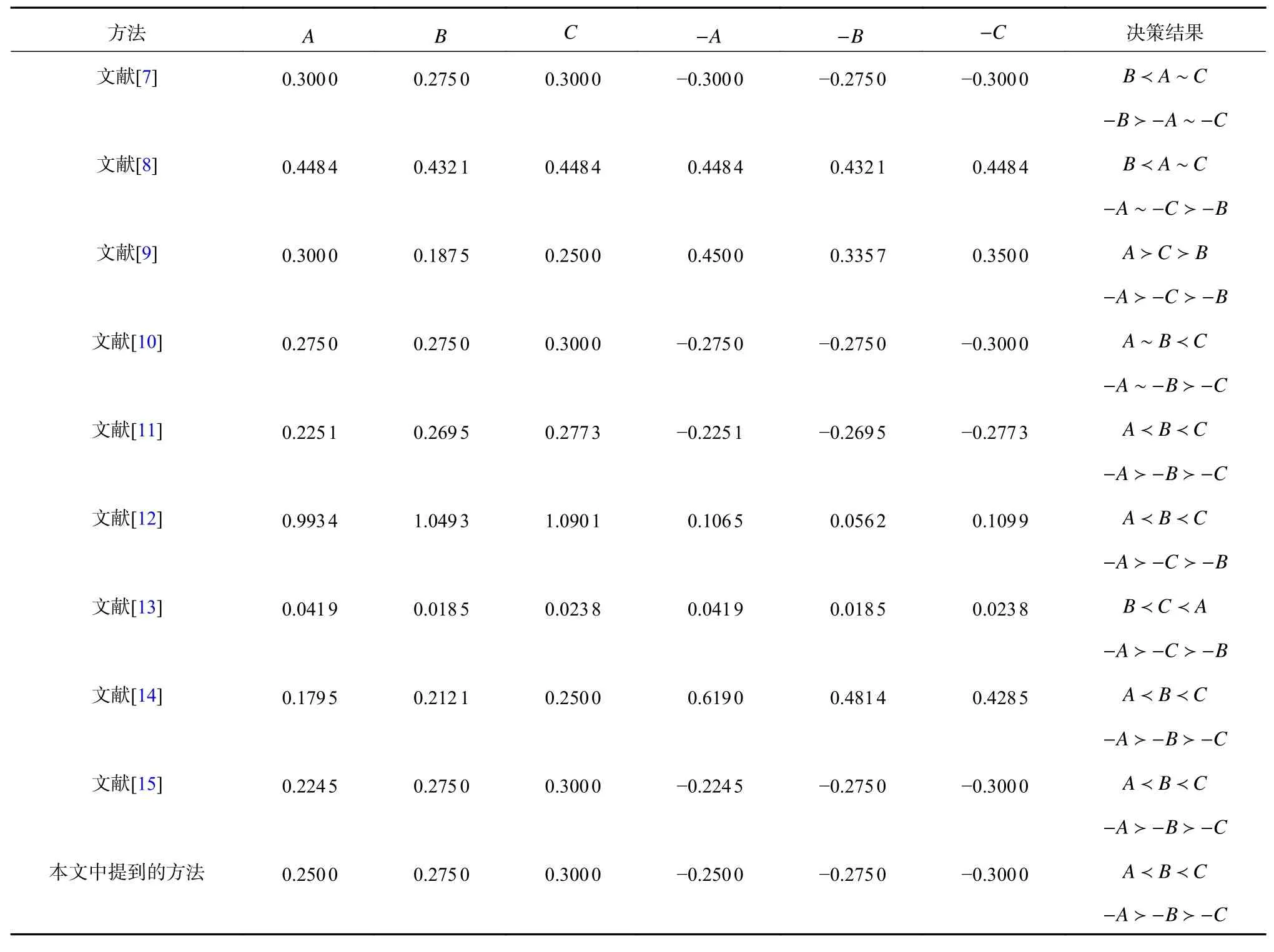
表3 例3 中的模糊數排序Tab.3 Ranking of fuzzy numbers in Example 3。

例4：假設有另一組簡單的例子A=(1.0,1.0,1.0,1.0;1.0)，B=(1.0,1.0,1.0,1.0;0.8)和C=(1.0,1.0,1.0,1.0;0.5)。直觀上，這些模糊數的排序應該是A?B?C，通過各種方法對這3 個模糊數進行排序，如表4。從表中可以看出，文獻[7]、文獻[8]和文獻[13]的方法無法區分這些模糊數。文獻[9]、文獻[14]和文獻[15]的方法認為這些模糊數及其圖像是相同的，這是不合邏輯的。此外，即使這些模糊數不同，但決策者的偏好水平也認為這些模糊數是相同的。因此，表中的大多數方法不能區分具有相同支撐的不同高度的精確值模糊數。由于質心點的期望不受模糊數高度的影響，所以產生了這種限制。然而，本文提出的方法可以克服這些限制，對這些模糊數及其圖像的排序分別為A?B?C和-C?-B?-A，這是符合人類直覺，是合乎邏輯的并且與文獻[10]和文獻[11]結果一致。

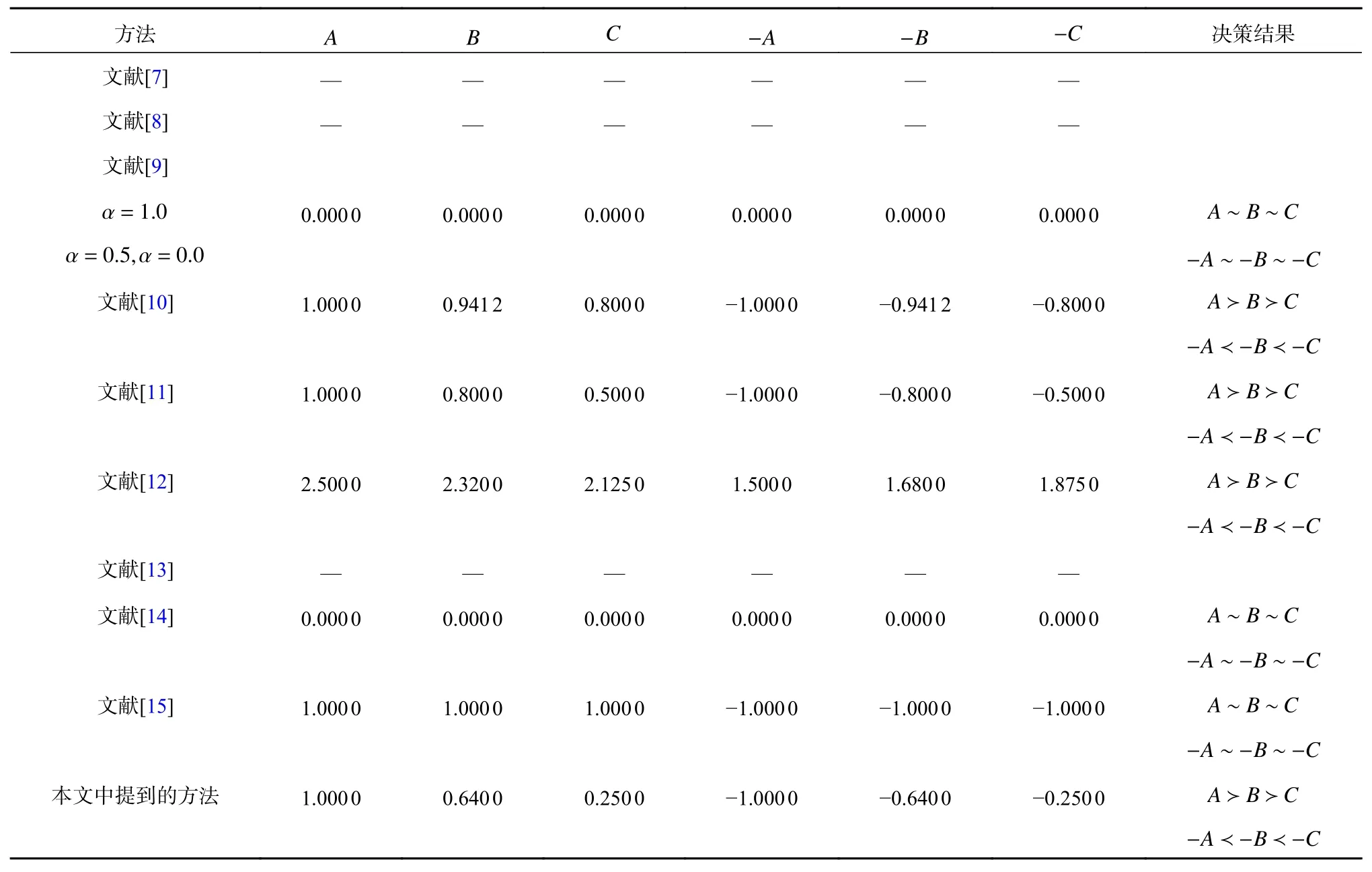
表4 例4 中的模糊數排序Tab.4 Ranking of fuzzy numbers in Example 4 。

4 結論

通過回顧可以看出，現有的排序方法大都不能對某些模糊數進行排序。因此，提出了一種基于模糊數的值以及左、右偏離度的新排序方法。在第4 節中描述的數值例子展示了所提出的方法如何在各種情況下優于其他方法。在例1 中，該方法可以清晰地對具有相同支撐和不同核的模糊數進行排序。從例2 中我們可以看出，現有的大多數方法無法對兩個具有面積補償的模糊數進行排序，而本文中提到的方法可以對這兩個模糊數以及它們的圖像作出正確的排序。在例3 中，當模糊數具有相同的質心和不同的支撐時，大多數方法無法對其做出正確的排序，但是利用本文的方法可以得到合乎邏輯的排序。此外，在例4 中該方法還可以對不同高度且具有精確值的模糊數進行排序，這些模糊數在大多數的研究中常常被忽略。從以上例子可以看出，在排序方法中引入模糊數的值和左、右偏離度是非常合理的，并且得到的結果也完全符合人類的直覺，克服了傳統的排序方法無法對某些模糊數進行排序的局限性。