一個新的涉及高階導函數與部分和的半離散Hilbert型不等式

王愛珍,楊必成

(廣東第二師范學院 數學學院,廣州 510303)

0 引 言

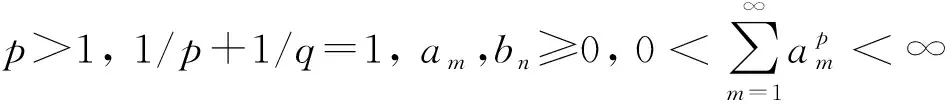
(1)

文獻[2]通過引入參數λi∈(0,2](i=1,2),λ1+λ2=λ∈(0,4],應用Euler-Maclaurin求和公式及實分析技巧建立了式(1)的如下推廣式:

(2)

這里常數因子B(λ1,λ2)是最佳的,

(3)

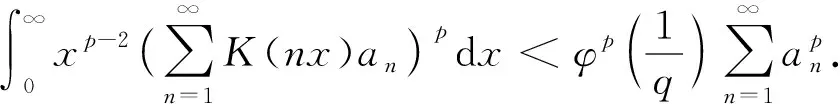
(4)

文獻[16-20]對式(4)進行了一些推廣和應用;文獻[21]應用實分析技巧給出了式(1)推廣式中最佳常數因子聯系多參數的一個等價陳述;文獻[22-28]進行了類似的研究;文獻[29-30]給出了逆向半離散Hilbert型不等式的一些新結果.

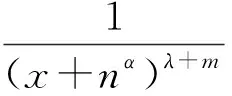
1 引 理

為避免重復陳述,本文設:p>1,1/p+1/q=1,m∈在+=(0,∞)上非負且除有限點外連續,f(k-1)(x)在+上可微且f(k-1)(0+) =0(k=1,2,…,m);對于an≥0,定義部分和(n∈N1={1,2,…}),滿足條件An=o(etnα) (t>0,n→∞).并設

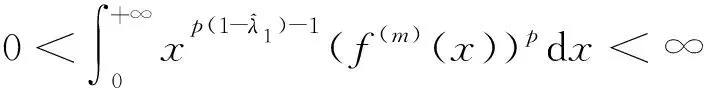
(5)

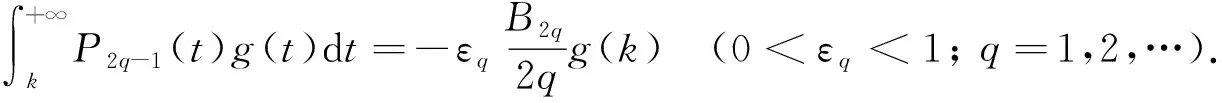
(6)

特別地,在式(6)中取q=1,由B2=1/6,有

(7)

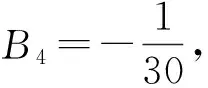
(8)

(ii) 若h(t)(>0)∈C3[k,∞),h(i)(∞)=0(i=0,1,2,3),則有如下Euler-Maclaurin求和公式:

引理2設s∈(0,6],s2∈(0,2/α]∩(0,s),ks(s2)∶=B(s2,s-s2),定義下列權函數:

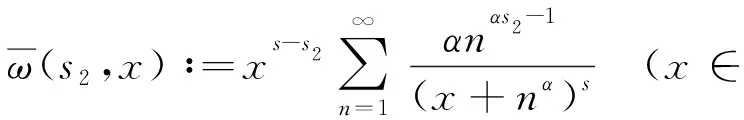
(11)

則有如下不等式:

(12)

由式(7)～(10),可求得

于是可得

定義函數g(σ)(σ∈(0,2/α])如下:

g(σ)∶=720-(420α+6sα2)σ+(60α2+5sα3)σ2-sα4σ3.

對于α∈(0,1],s∈(0,6],可求得

對于s2∈(0,2/α],有

因此有h(x)>0.做變換t=x1/αu1/α,有

因此,式(12)成立.證畢.

引理3設s∈(0,6],s1∈(0,s),s2∈(0,2/α]∩(0,s),則有如下不等式:

證明: 做變換u=x/nα,可求得如下另一個權函數表示式:

(14)

由H?lder不等式[31],有

再由式(12),(14)有式(13)成立.證畢.

注1在式(13)中,設s=λ+1∈(0,6],λ∈(-1,5],s1=λ1∈(0,λ+1),s2=λ2+1∈(0,2/α]∩(0,λ+1),λ2∈(-1,2/α-1]∩(-1,λ).置換f(x)(an)為f(m)(x)(An),由條件式(5),可得如下含新參數的不等式:

引理4對于t>0,有

(16)

(17)

證明: 因為f(m)(x)≥0,所以f(m-1)(x)在+上遞增.又因為f(m-1)(0+)=0,所以f(m-1)(x)≥0.由歸納法,由f(k)(x)≥0,有f(k-1)(x)在+上遞增,又由f(k-1)(0+)=0,可得f(k-1)(x)≥0(x>0;k=1,2,…,m).對于m=0,式(16)取等號成立;當m≥1時,由分部積分法,可得

用k=1,2,…,m疊加易得式(16).

因為Ane-tnα=o(1)(n→∞),故由Abel部分求和公式,有

由不等式1-e-t0)及對于α∈(0,1],有

從而有

即式(17)成立.證畢.

2 主要結果及應用

定理1若λ∈(-1,5](λ>-m),λ1∈(0,λ+1),λ2∈(-1,2/α-1]∩(-1,λ),則有如下涉及高階導函數和部分和的半離散Hilbert型不等式:

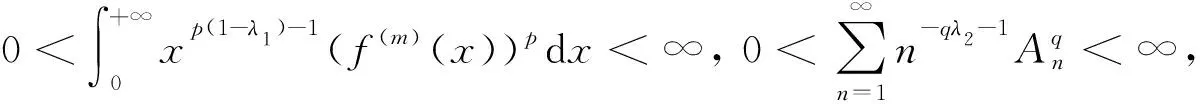
再由式(15)有式(18).證畢.

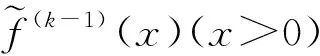
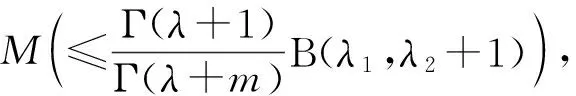
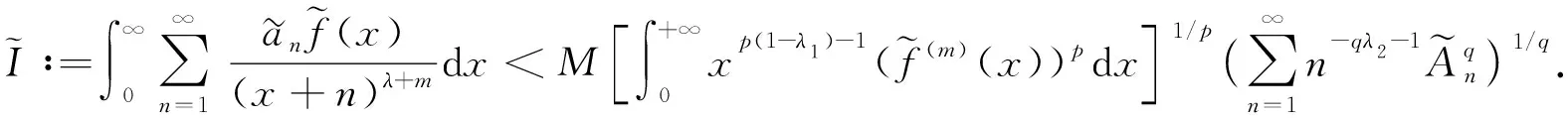
(20)

由式(20)及級數的遞減性質,可得

計算可得

由式(14),可得

基于上述結果,有

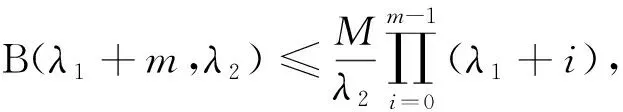
(22)

式(21)取等號的充分必要條件是存在不全為0的常數A和B,使得Auλ-λ2-1=Buλ1-1a.e.于+[31].不妨設A≠0,則有于+,λ-λ2-λ1=0.因而有λ1+λ2=λ.證畢.

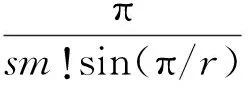
(23)

特別地,當r=p,s=q時,有

(24)

當r=q,s=p時,有

(25)

當p=q=2時,式(24)和式(25)均變為如下Hilbert型不等式:

(26)

上述不等式的常數因子都是最佳值.