如何幫助學生理解“積的變化規律”

陳金波

教學中，教師可以引導學生利用直觀圖式，通過不完全歸納的方式，幫助學生深入理解“積的變化規律”。具體可以采用以下教學方式。

一、利用直觀圖式，感知規律

1.直觀感知，初步感知

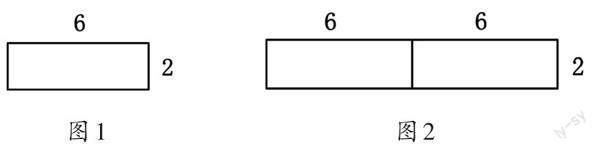
教師呈現圖1，讓學生列式計算這個長方形的面積是多少。接著呈現圖2，讓學生列式計算大長方形的面積是多少。引導學生思考：比較圖1中的長方形和圖2中的大長方形，什么變了？什么沒變？

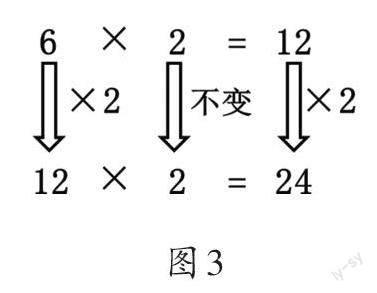
教師根據學生的回答，逐步呈現箭頭圖（如圖3）。

得出結論：在乘法算式中，一個因數乘2，另一個因數不變，積也乘2。

2.自主探究，發現規律

教師給出學習任務：在學習單上畫一個由四個圖1這樣的小長方形組成的大長方形，并寫一寫長方形的長、寬和面積會發生怎樣的變化。

逐一反饋不同的學生作品。

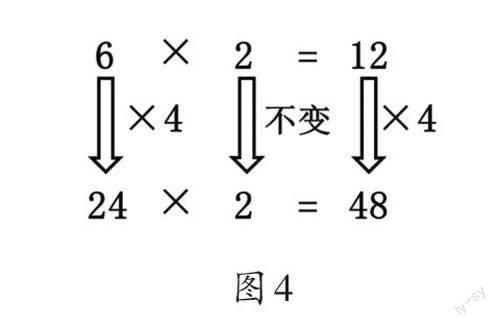
學生作品1：長方形的長變化，寬不變（如圖4）。

得出結論：在乘法算式中，一個因數乘4，另一個因數不變，積也乘4。

學生作品2：長方形的長不變，寬變化（如圖5）。

得出結論：在乘法算式中，一個因數不變，另一個因數乘4，積也乘4。

學生作品3：長方形的長和寬都發生變化（如圖6）。

得出結論：在乘法算式中，一個因數乘2，另一個因數乘2，積乘4。

3.比較算式，猜測規律

通過比較圖3、圖4、圖5、圖6中的算式，猜想：因數和積之間存在什么樣的規律？

二、通過不完全歸納，形成規律

1.獨立思考

通過對這些算式的觀察、比較，發現因數和積之間存在共同變化的規律，那么在其他乘法算式中是否也有這樣的規律呢？

2.舉例驗證

先寫一個乘法算式，然后分別觀察一個因數不變，另一個因數發生變化，以及兩個因數都發生變化兩種情況下積會怎樣變化。

3.形成規律

通過舉例驗證，學生發現有舉不完的例子。在此基礎上，讓學生用語言表達規律。

三、借助多維度觀察，完善規律

1.多維度觀察

通過觀察小長方形組合成大長方形時其長、寬和面積的變化，學生已經發現了因數和積之間的部分變化規律。在此基礎上，組織小組討論：如果將大長方形縮小為小長方形（如圖7），你能發現什么規律？

2.完善規律

在原有舉例的基礎上，讓學生畫一畫、寫一寫，說一說新的發現，完善對規律的認識。特別是要引導學生思考：為什么要“0除外”？

3.質疑問難

引導學生根據自己的學習過程提出問題，如：在乘法算式中，一個因數乘4，另一個因數除以2，積會怎樣變化？

以上教學通過層層推進，讓學生在不斷學習進階中，逐步理解積的變化規律。