縱波與橫波反演能力對比

代福材，張峰*，錢忠平，孫鵬遠，鄒振，李向陽，3

（1. 中國石油大學（北京）油氣資源與探測國家重點實驗室，北京 102249；2. 中國石油大學（北京）CNPC 物探重點實驗室，北京 102249；3. 東方地球物理公司，河北涿州 072750；4. 油氣勘探計算機軟件國家工程研究中心，北京 100088）

1 問題的提出

目前，油氣地震勘探主要利用了縱波（PP 波）的信息。縱波對地層的聲波速度、阻抗的變化最為敏感，在構造成像、斷層解釋等方面得到了廣泛應用；結合巖石物理分析可以在一定程度上描述儲層特征［1］、識別孔隙流體的變化［2-3］。油氣藏的定量解釋依賴于利用地震數據反演所獲得的地層參數，而僅利用有限角度（炮檢距）的縱波數據同步反演多個彈性參數比較困難［4-5］。其中，密度（ρ）反演尤為困難，這是因為縱波對密度的變化不敏感［6］。實例表明，為了準確反演地層密度，需要使用經過各向異性偏移成像、子波拉伸校正、吸收衰減補償等處理的大角度（60°）縱波數據，同時還要保證初始模型可靠、正則化方法適用［7］，而在許多實際勘探工作中難以滿足以上條件。雖然兩參數（縱波阻抗和橫波阻抗、AVO 截距和梯度等）反演方法比三參數（如縱波阻抗、橫波阻抗、密度）反演更加可行，但是反演結果存在一定的誤差和不確定性，這同時對數據和反演方法有著較高的要求［8-9］。此外，縱波在“氣煙囪”成像、復雜和非常規油氣藏的巖性識別、流體預測等方面也存在困難［10-11］。

相比于縱波，橫波（SV-SV 波和SH-SH 波）的動力學特征有著顯著的差異。在同一頻帶、相同的吸收衰減條件下，橫波數據的分辨率更高，對地層的橫波速度（VS）、密度、剪切模量、各向異性參數等更為敏感，因此可以用來更好地反演以上參數。如圖1所示，相比縱波資料，橫波資料在反演橫波速度、密度等參數時不確定性更低，在描述油氣藏的骨架性質、物性特征、裂縫、地應力等方面具有明顯優勢［12-16］。因此，將橫波引入油氣勘探能夠彌補縱波勘探能力的不足，有助于提升復雜油氣藏的儲層預測精度和油氣識別能力［17-19］。

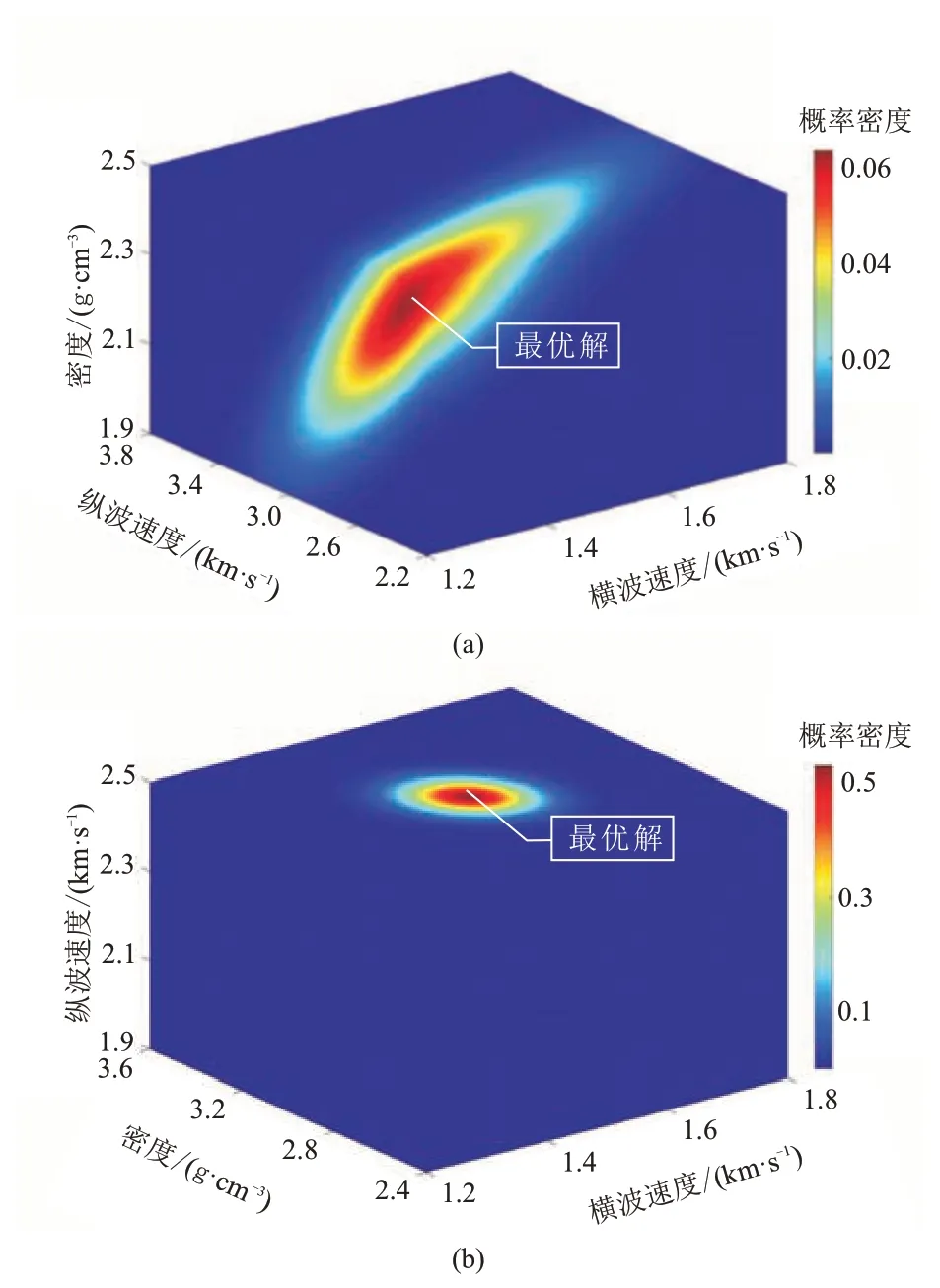
圖1 PP 波（a）與SH-SH 波（b）反演縱波速度、橫波速度、密度的后驗概率密度分布

為了明確橫波的傳播機理，諸多學者開展了理論研究［20-25］。橫波曾在早期被應用于地震勘探［26-28］，通過多分量地震采集得到的橫波各向異性屬性用于裂縫油氣儲層描述［29-30］，但在較長的一段時期內，橫波并沒有在油氣勘探中得到廣泛應用，主要是因為傳統的橫波震源技術無法獲得高品質數據。

轉換橫波不依賴于震源，可以通過爆炸源和垂直力源激發、三分量檢波器接收，因此從20世紀90年代開始，它作為橫波的替代應用于油氣勘探。目前，業界已針對轉換波數據的處理和成像開展了大量的研究工作［31-35］。實際應用結果表明，由于橫波傳播基本不受流體影響，轉換橫波在氣云區成像方面具有一定的優勢［36］；聯合反演縱波和轉換橫波數據有助于改善地層橫波速度和密度的反演結果，提高了反演穩定性和精度［37-39］。然而，相比縱波，轉換橫波的數據品質往往較低，難以獨立應用于儲層的精細描述。縱波和轉換波聯合反演的效果在很大程度上依賴于縱、橫波數據的匹配精度，這導致聯合反演方法在實際應用中受到一定程度的制約。

近年來，大噸位、寬頻橫波可控震源技術在油氣勘探行業中迅速發展，可以激發與縱波數據品質相當的SV-SV 波和SH-SH 波［40-44］，為橫波油氣勘探技術的發展和廣泛應用提供了良好的基礎。但是，目前地震橫波的反演理論尚不完善，有必要進一步開展縱波與橫波的反演能力對比、分析，為橫波反演方法研究提供理論依據。為此，本文首先介紹了不同類型地震波反射系數的近似式，并通過與精確反射系數對比分析近似式的精度；然后構建針對不同彈性參數的線性反演框架，計算不同待求參數組合的反演協方差矩陣，對比PP 波、PSV 波、PP 波和PSV波聯合、SH-SH 波、SV-SV 波在反演不同彈性參數時的不確定性；進而通過計算不同類型地震波反演的特征值和條件數，對比、分析反演問題的不適定性；最后以反演協方差矩陣和反演條件數為依據明確了不同類型地震波的反演能力及橫波反演方法的應用潛力。

2 不同類型地震波反射系數近似公式

不同彈性參數表示的反射系數近似式廣泛應用于地震反演，因此在介紹PP 波、PSV 波、SH-SH 波、SV-SV 波反射系數近似式基礎上，通過與精確反射系數對比分析其精度。

2.1 PP 波

PP波的反射系數近似式為［45-46］

根據彈性參數之間的關系，可得到利用縱波阻抗IP、橫波阻抗IS等參數表示的近似式為［47］

利用IP、剪切模量μ等參數表示的近似式可表示為

對比PP 波反射系數近似式與精確公式，分析近似式在不同入射角的精度。采用的彈性界面參數如表1 所示，其中模型1 和模型2 均為弱阻抗差，模型3和模型4均為強阻抗差。

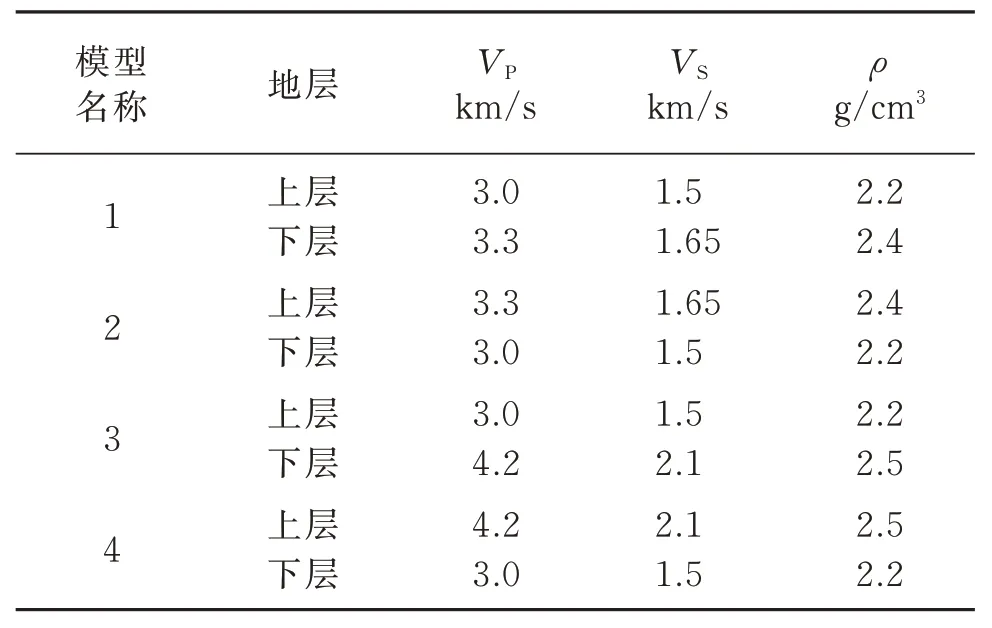
表1 不同模型彈性參數

由圖2 可見，式（1）～式（3）的精度基本相同。在弱阻抗差情況下（圖2a、圖2b），反射系數近似式在入射角50°以內保持較高的精度；在強阻抗差情況下（圖2c、圖2d），雖然在臨界角附近的精度有所下降，但在入射角30°以內依然保持較高的精度。由此可以得出結論，PP 波反射系數近似式可用于后續反演能力分析。

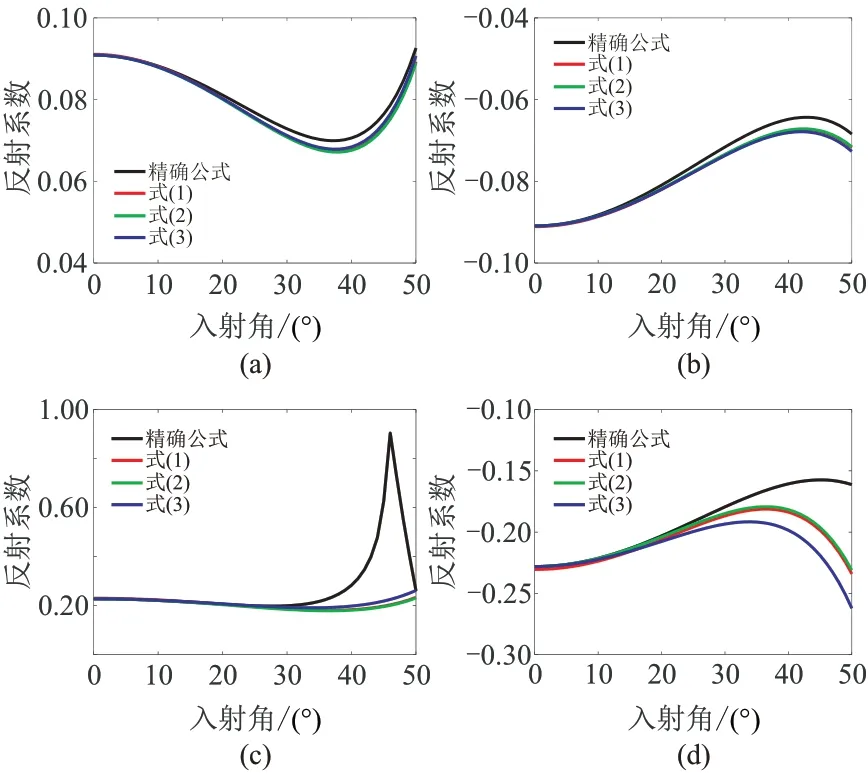
圖2 PP 波反射系數近似式精度分析

2.2 PSV 波

PSV 波的反射系數近似式為［48］

式中θ和?分別表示PP 波的入射角和PSV 波的反射角。

在此基礎上，根據彈性參數之間的關系可進一步整理得到IS和ρ表示的近似式

利用μ和VS表示的近似公式為

從式（4）～式（6）可以看出，PSV 波的反射系數近似式雖然只含有2 個待反演的模型參數，但是由于公式中還包含了θ、?、γ，因此實際上各個待求參數的系數并不是“參數獨立”的。在實際反演時，反射系數公式中的系數項對待求參數的先驗信息的依賴性較高。

對比PSV 波反射系數近似式與精確式，分析近似式在不同入射角的精度。同樣采用表1所示的彈性參數。

由圖3 可見，式（4）～式（6）的精度基本相同。在弱阻抗差情況下，反射系數近似式在入射角50°以內保持較高的精度；在強阻抗差情況下，雖然在臨界角附近的精度有所下降，但在入射角30°以內仍然保持較高的精度。

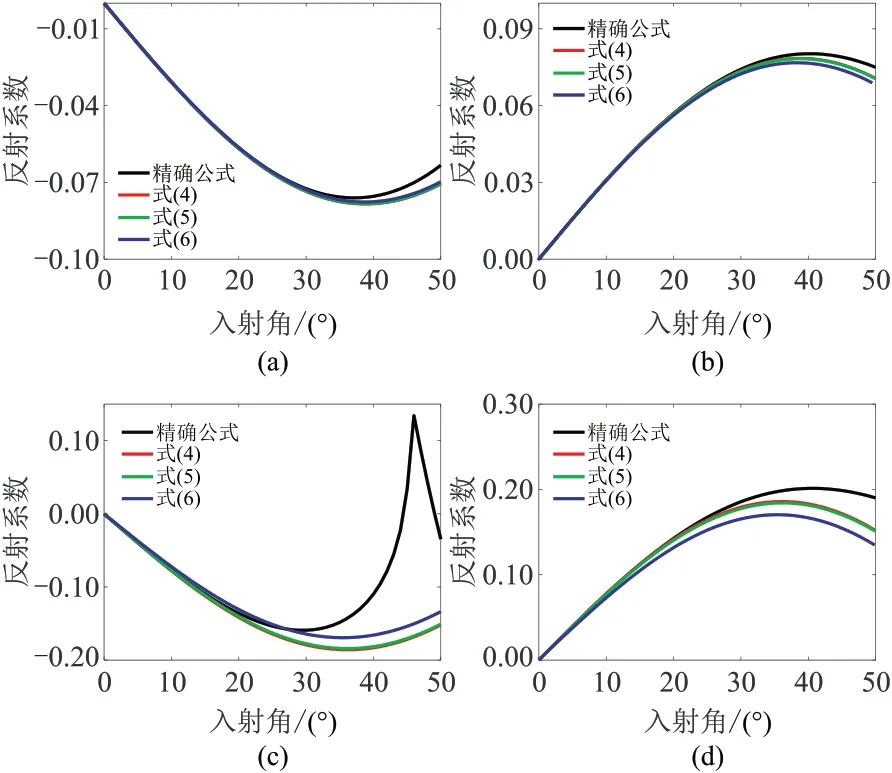
圖3 PSV 波反射系數近似式精度分析

2.3 SH-SH 波

SH-SH 波反射系數的精確式可表示為［49］

式中?1和?2分別表示SH波的入射角和透射角。根據上式，SH波的反射特征僅與地下介質的2個參數（橫波速度和密度）有關，這與PP波的反射特征有顯著差異。

將式（8）代入式（7），忽略二階以上高階項，可推導出用VS和ρ表示的SH-SH波反射系數的近似式［50］

在此基礎上，可進一步推導得到利用IS和VS表示的近似式

利用μ和VS表示的近似式為

從式（9）～式（11）可以看出，SH-SH 波的反射系數方程都具有非常簡單的表達形式，即每個方程只含有2個待反演的模型參數（如式（9）中的VS和ρ），并且各個待求參數的系數是“參數無關的”，在實際反演時無需依賴待反演參數的先驗信息。

對比SH-SH 波反射系數近似式與精確公式，分析近似式在不同入射角的精度，同樣采用表1 所示的彈性參數。

由圖4可見，式（9）～式（11）的精度基本相同。在弱阻抗差情況下，反射系數近似式在入射角50°以內保持較高的精度；在強阻抗差情況下，雖然由于臨界角導致精度有所下降，但在入射角30°以內仍然保持較高的精度。

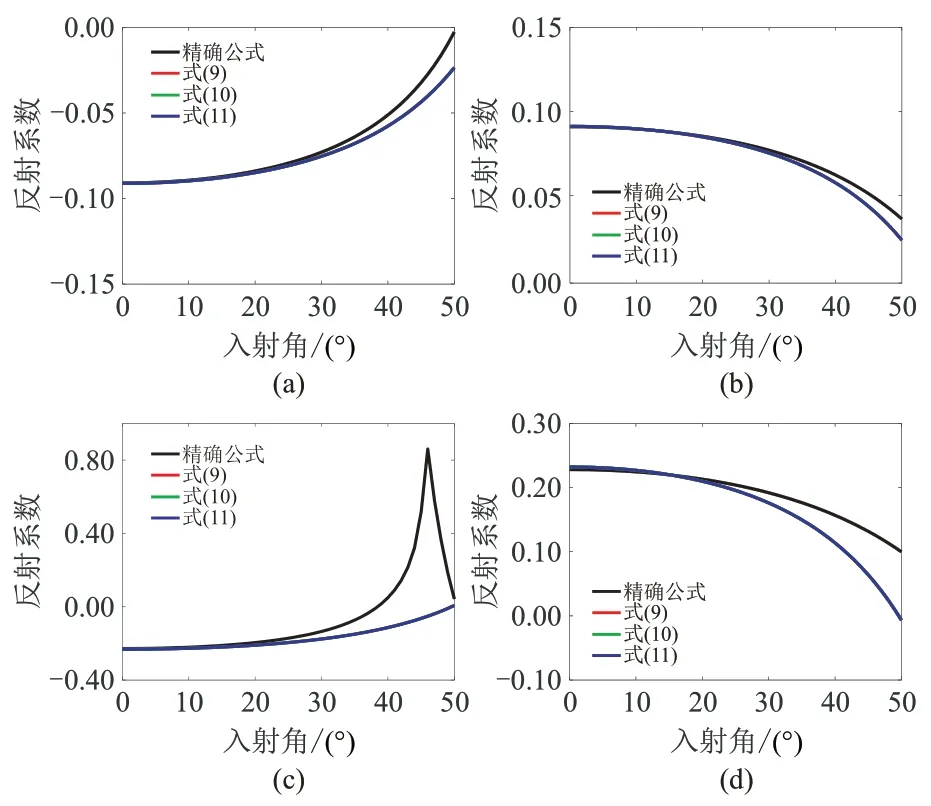
圖4 SH-SH 波反射系數近似式精度分析

2.4 SV-SV 波

Zhang［51］推導了用VS和ρ表示的SV-SV 波反射系數的改進公式，即

式中為SV 波入射角和透射角的平均值。根據彈性參數之間的關系，可推導得到IS和VS表示的近似式

利用μ和VS表示的近似式可表示為

從式（12）～式（14）可以看出，SV-SV 波近似式中的與地層的橫波速度有關，因此SV-SV 波反射系數近似式中各個待求參數的系數不僅與角度有關，同時也受介質VS的影響，并非完全“參數無關的”，并且SV-SV 波反射系數由于受縱波速度的隱性影響導致存在多個臨界角。在VS2>VS1時，三個臨界角分別為多臨界角會導致近似式在臨界角處出現較大誤差。

對比SV-SV 波反射系數近似式與精確公式，分析近似式在不同入射角的精度，同樣采用表1 所示的彈性參數。

由圖5 可見，反射系數近似式式（12）～式（14）的近似精度基本相同。在弱阻抗差情況下，反射系數近似公式在入射角50°以內保持較高的精度；在強阻抗差情況下，多臨界角現象導致近似式精度大幅下降（在模型3時，第一個臨界角約為21°），僅在入射角20°以內保持較高精度。

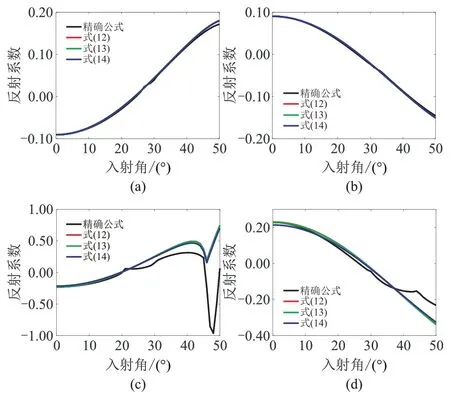
圖5 SV-SV 波反射系數近似式精度分析

綜上所述，不同類型地震波反射系數近似式在弱阻抗差（模型1 和模型2）的情況下，入射角50°以內均保持較高的近似；在強阻抗差（模型3和模型4）的情況下，近似式的精度出現了不同程度的下降，這是由于近似式的推導是基于弱阻抗假設條件的。因此，在后續的反演分析中，本文采用的最大入射角為50°，反射系數近似式的精度可滿足理論分析的需求。

3 基于協方差矩陣的反演不確定性分析

3.1 方法原理

根據不同類型地震波的反射系數近似式可以構建一個線性正演方程

式中R、F、m分別表示反射系數（觀測數據）、正演算子（映射關系）、模型參數（待求參數）。

根據貝葉斯原理，待求參數的后驗概率密度分布的最大值是其期望值，參數的方差可描述后驗概率密度分布與期望之間的離散程度，因此方差可用于描述參數估計的不確定性。參數協方差矩陣的對角線元素表示每個參數估計的方差，而非對角元素表示不同變量之間的相關性，因此參數協方差矩陣可用于研究反演中的不確定性。本文采用Downton［8］和Zhang等［52］的方法，通過計算待求參數的協方差矩陣Cm，定量分析反演的不確定性。當數據噪聲滿足高斯分布，并且符合均勻、不相關的假設，則協方差矩陣Cm可通過下式計算

式中：σn為估算的數據噪聲標準差；不同類型地震波的F矩陣具體形式見附錄A。

利用不同彈性參數表示的反射系數近似式可得到對應的待求參數組合。本文分別計算了最大入射角度分別為30°、40°、50°時的反演協方差矩陣。協方差矩陣中某元素的數值越大，表明反演該元素對應的參數的不確定性越大。結合前人的研究成果，本文將反演協方差矩陣中元素值小于0.05 作為反演不確定性較小的定量評價標準。

3.2 結果分析

3.2.1 PP 波

PP波在不同最大角度下的反演協方差矩陣如圖6所示。由圖可見，對于所有的待求參數組合，反演協方差矩陣中各元素的數值都隨著PP 波數據的最大入射角度的增加而減小，這表明入射角度越大，反演各個參數的不確定性越小。當PP 波數據的最大角度為30°時，只有IP的不確定性較小，而其他參數的不確定性都很高（圖6a），這表明當使用小角度（<30°）的PP波數據反演其他參數時，反演結果的準確性在很大程度上依賴于數據的品質、初始模型的可靠性、正則化方法等。當PP 波數據的最大角度達到40°時，IS的不確定性明顯降低，但是其他參數的不確定性仍然很高（圖6b）。當PP 波數據的最大角度達到50°時，所有參數的不確定性都能夠降低到相對理想的數值（各參數的協方差<0.05），但是ρ和μ的不確定性相比于縱、橫波阻抗仍然較高（圖6c中和圖6c右）。因此，相比于其他參數，需要輸入較大角度的數據（>50°），PP 波才可準確反演ρ和μ。

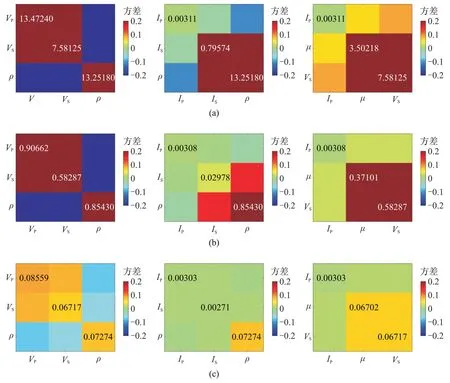
圖6 不同角度數據PP 波反演不同彈性參數時的協方差矩陣

3.2.2 PSV 波

PSV 波在不同入射角下的協方差矩陣如圖7 所示。由圖可見，當PSV 波的最大角度為30°時，只有IS的不確定性較小，其他參數的不確定性都很高（圖7a）；當最大角度達到40°時，各參數的不確定性明顯降低（各參數的協方差<0.1， 圖7b）；當最大角度達到50°時，所有參數的不確定性都非常低（各參數的協方差都接近0， 圖7c）。以上角度均為縱波入射角，在縱、橫波速度比為1.25 時，對應的橫波反射角分別為23.6°、30.9°、37.8°。值得注意的是，相比于縱波數據，PSV 波數據品質相對較低，并且由于PSV波傳播路徑的不對稱性導致其數據處理流程較為復雜，難以獨立應用于精細的儲層描述，一般應聯合應用PSV 波和PP 波數據以提升反演穩定性和解釋的精度。

3.2.3 PP 波和PSV 波聯合反演

由于單獨利用PP 波反演ρ、μ等參數會存在較大的不確定性，在實際應用中，通常加入PSV 波信息，利用PP-PSV 波聯合反演以減少反演的不確定性。

根據PP 波和PSV 波近似式（式（1）～式（6）），PPPSV 波聯合反演不同參數的不確定性如圖8 所示。由圖可見，當最大角度（縱波入射角）為30°時，IP和IS的不確定性較小，其他參數的不確定性相比PP 波反演有所下降，但仍然較高（圖8a）；當最大角度達到40°時，各參數的不確定性明顯降低（各參數的協方差<0.05，圖8b）；當最大角度達到50°時，所有參數的不確定性都非常低（各個參數的協方差都接近0，圖8c）。在縱、橫波速度比為1.25 時，對應的橫波反射角分別為23.6°、30.9°、37.8°。結果表明：相較于單獨使用PP 波，聯合使用PP 波和PSV 波在反演ρ和μ等參數時具有明顯優勢。PSV 波數據的處理過程比純波（PP 波、SV-SV 波、SH-SH 波）更為復雜，因此在實際應用中，聯合反演的效果很大程度上依賴于縱、橫波數據的匹配精度，而實際上地震縱、橫波數據的高精度匹配仍然存在一定的困難。

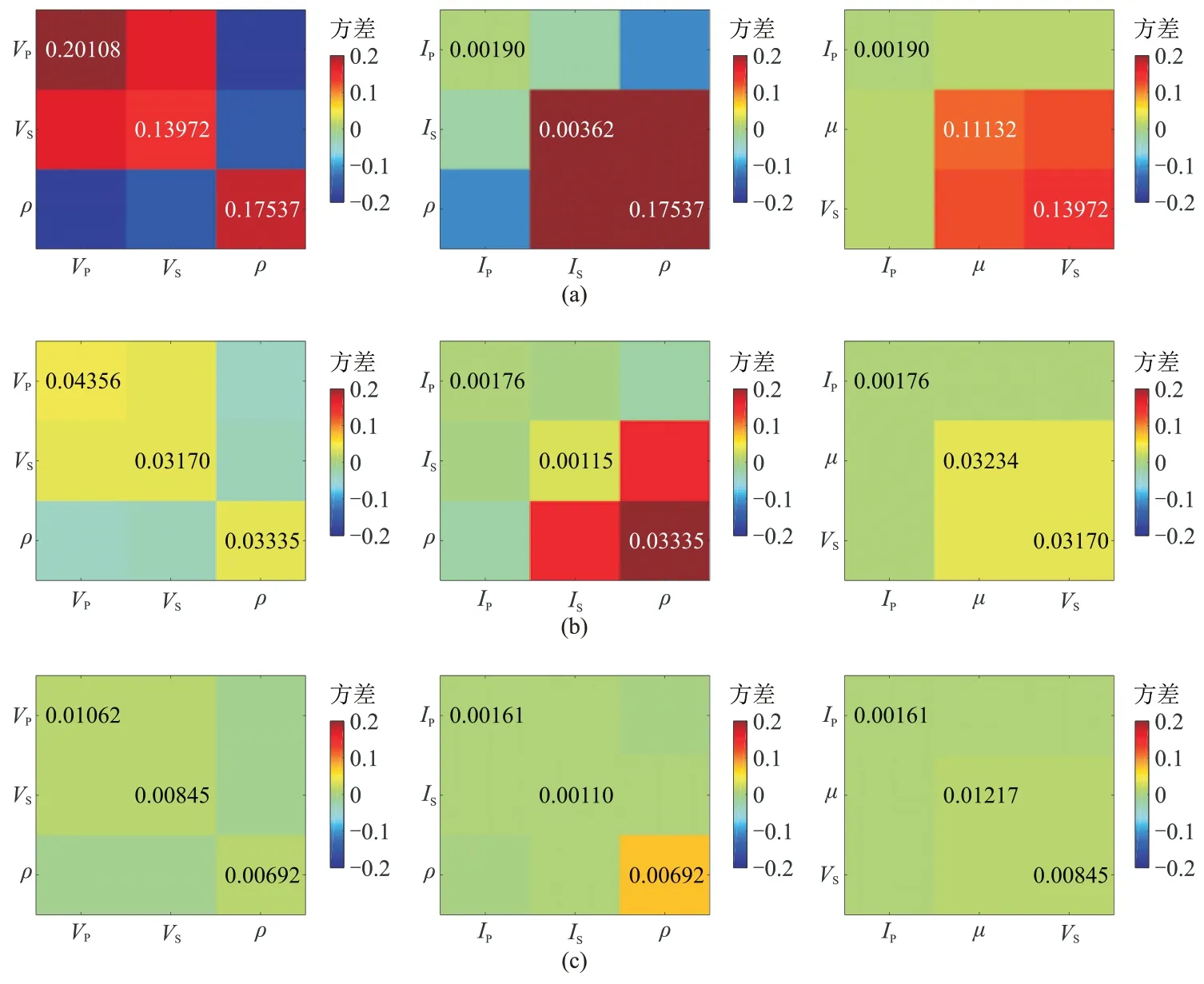
圖8 不同角度PP 波和PSV 波聯合反演不同彈性參數時的協方差矩陣

3.2.4 SH-SH 波

SH-SH波反演不同彈性參數的不確定性如圖9所示。由圖可見，即使使用小角度的數據（<30°），SH-SH波反演IS、VS、ρ、μ的不確定性也較小（圖9a），參數協方差的數值基本與PP 波最大入射角為50°時的反演結果相當。當SH-SH 波數據的最大角度達到40°時，各參數的不確定性進一步降低（各參數協方差<0.05，圖9b）；當最大角度達到50°時，反演的不確定性已經非常小（各參數的協方差接近0，圖9c）。相比于PP波，SH-SH 波在反演ρ和μ等參數時具有明顯的優勢。此外，SH-SH 波的反射系數近似式中各個待求參數的系數是“參數無關的”。在實際反演時，SH-SH 波相比于PP 波和PSV 波（待求參數的系數與γ有關）對待求參數的先驗信息的依賴更小，并且SH-SH 波僅包含兩項待反演參數，因此可有效減少反演的病態性，提高反演的穩定性。

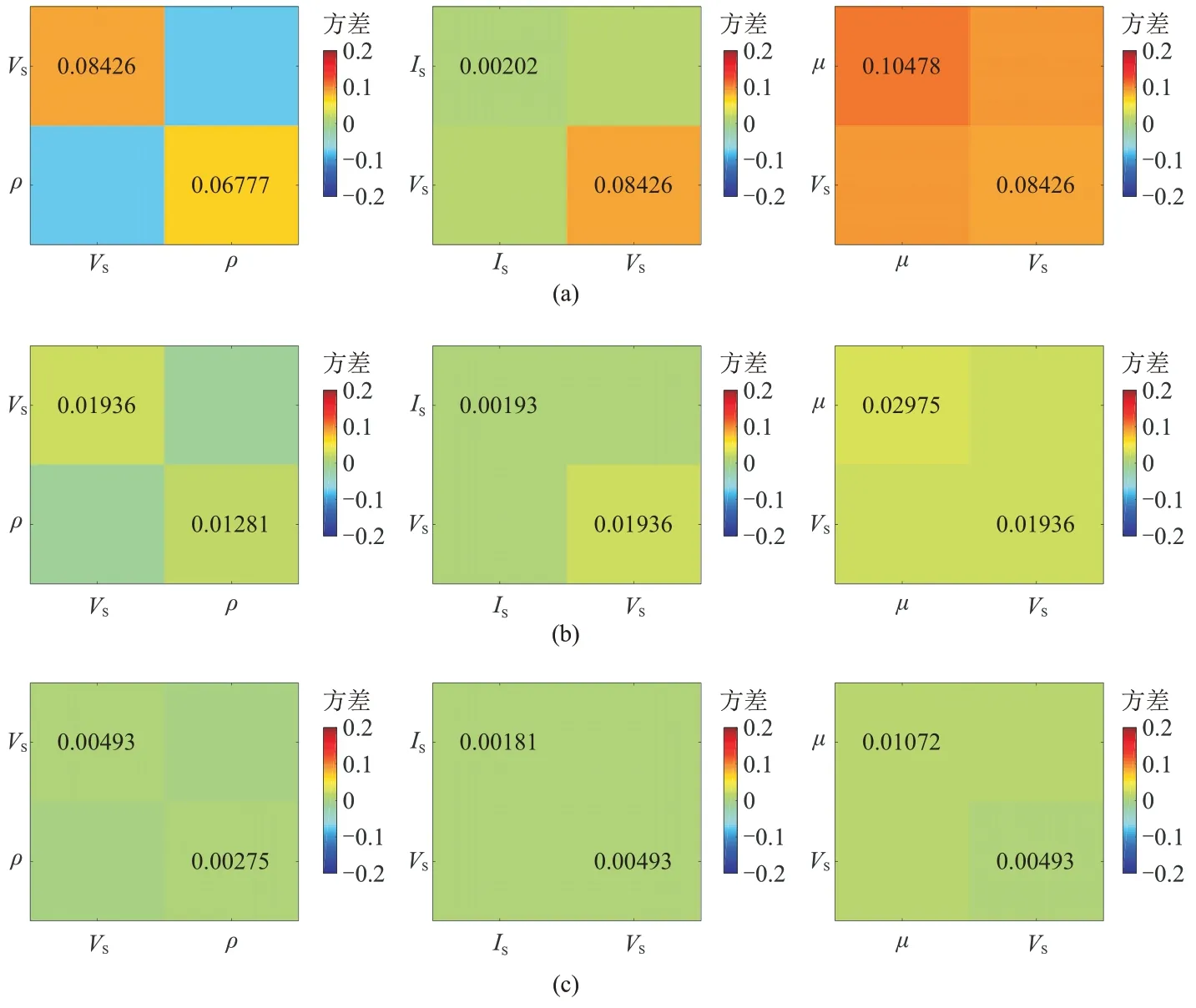
圖9 不同角度SH-SH 波反演不同彈性參數時的協方差矩陣

3.2.5 SV-SV 波

SV-SV 波的反演協方差矩陣如圖10所示。由圖可見，與PP 波相比，SV-SV 波在反演IS、VS、ρ、μ等參數時的不確定顯著降低。僅使用小角度（<30°）的SVSV 波數據即可穩定反演各個參數（各參數協方差<0.05， 圖10a），更大角度的數據對待求參數的不確定性的影響較小（圖10b、圖10c）。因此，相比于SH-SH波，SV-SV 波在反演不同彈性參數時對輸入數據的最大角度的需求更低。值得注意的是，SV-SV 波與SHSH 波雖同屬橫波，在各向同性介質中兩者具有相同的傳播速度，但是SV-SV 波與PP 波的偏振方向在同一平面，SH-SH 波的偏振方向垂直于前兩者所在的平面。因此，在實際數據的波場分離中，SV 波更容易受到P 波的影響［53］，而SH 波則與PP 波完全解耦，并且SV-SV 波存在多臨界角現象。因此，關于SV-SV 波反演和SH-SH 波反演的適用性需要結合實際數據具體分析。

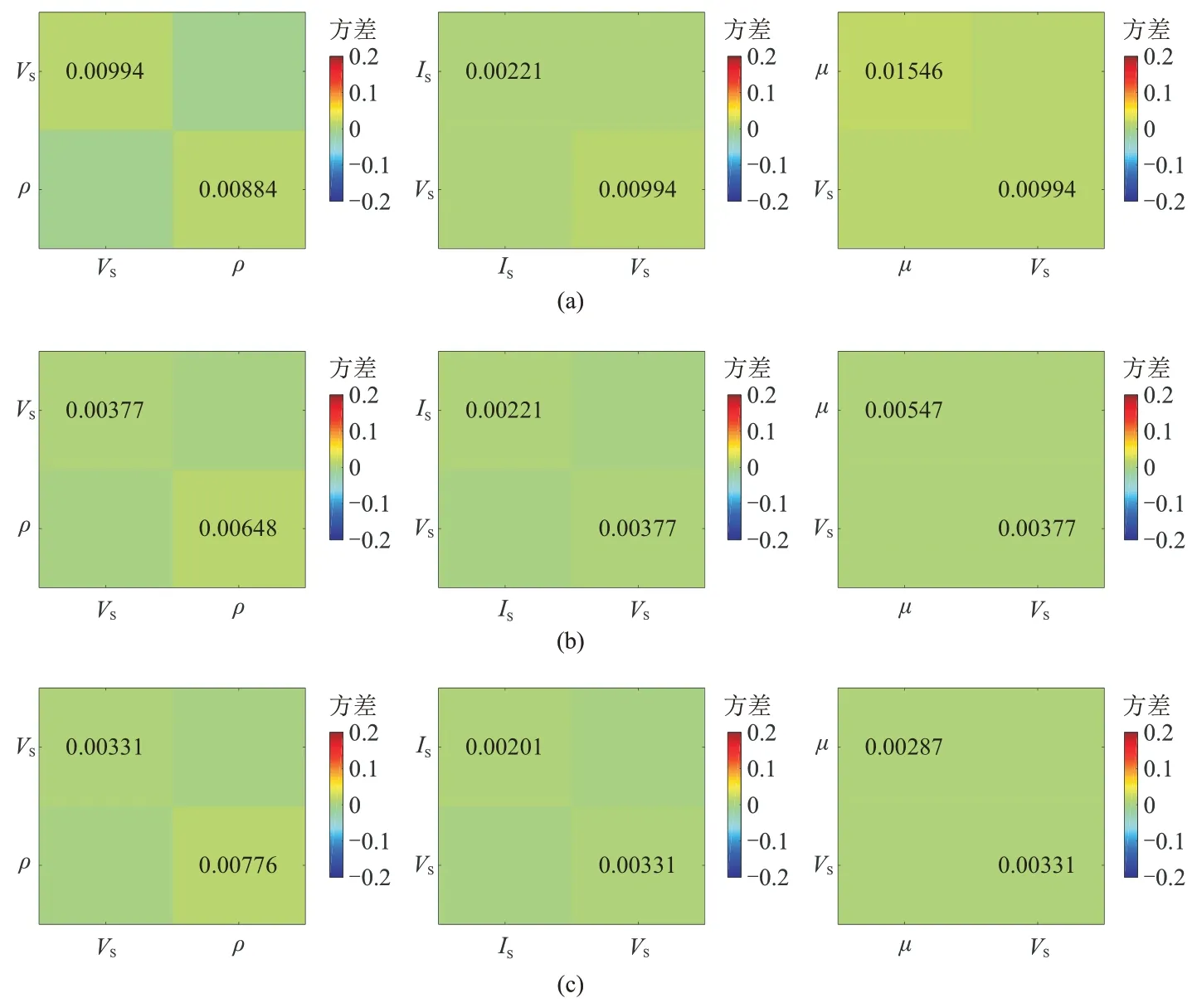
圖10 不同角度SV-SV 波反演不同彈性參數時的協方差矩陣

綜上所述，對于同一類型地震波的不同待求參數組合，反演的不確定性也存在一定差異。PP 波及PP波與PSV 波聯合反演的最佳待求參數組合為IP、IS和ρ；PSV 波的最佳待求參數為IS和ρ；SV-SV 波和SHSH 波的最佳待求參數為IS和VS。地震橫波（SH-SH波和SV-SV 波）在反演μ、ρ等參數時，相較于PP 波和PSV 波在反演能力和反演精度等方面有了顯著的提升。除此之外，地震橫波的數據處理流程與縱波類似，相較于轉換橫波的處理流程而言已大幅簡化，并且反演結果不依賴于高精度的縱、橫波數據匹配，因此在油氣儲層精細描述中具有很大的應用潛力。

4 基于特征值和條件數的反演不適定性分析

4.1 方法原理

在數據空間和模型空間可以將F奇異值分解（Singular Value Decomposition，SVD）為三個正交分量［54］

式中：Λ為特征值的對角矩陣；M表示模型空間的特征向量；D表示數據空間的特征向量（圖11）。特征值表示對應分量的能量，特征值越大表示模型參數對應的能量分量越大。如果不同參數的特征值相差較大，表示反演結果具有較強的病態性，需要大角度信息才可準確反演模型參數。因此，可根據不同角度的特征值分析反演的不適定性。

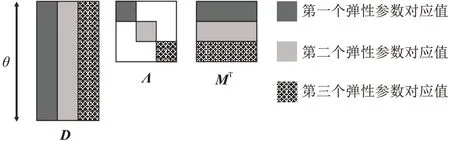
圖11 線性正演算子奇異值分解示意圖［54］

通常可以用條件數描述反演的不適定性，它為F的范數與F的逆的范數的乘積，即

對于反演而言，條件數較大的反演稱為病態，條件數較小的反演稱為良態。因此，可進一步利用條件數隨最大入射角的變化分析線性反演的不適定性。為便于直觀顯示，本文將特征值和條件數的單位均用dB（即20 lgλi，λi表示特征值）表示。由于條件數可表示為最大特征值與最小特征值的比值，在對數形式下，條件數即為最大特征值與最小特征值之差。

4.2 結果分析

根據不同反射系數近似式構建F，并對F進行奇異值分解可分析線性反演的不適定性。為了與前文近似精度分析保持一致，選擇最大入射角為50°，并將反演條件數小于20 dB 作為反演不適定性較小的定量評價標準，即彈性參數對應能量分量最大值與最小值相差10倍。

4.2.1 PP 波

根據PP 波反射系數近似式（式（1））構建F，計算得到的特征值及條件數隨最大入射角的變化情況如圖12 所示。由圖可見，VP特征值隨最大入射角變化較小，并且在三個特征值中一直最大，表示VP對應的能量分量最大；而ρ特征值最小，表示ρ對應的能量分量最小。雖然ρ特征值隨最大入射角增大而增大，但在最大角度為50° 時，ρ特征值與VP特征值仍相差30 dB 左右（圖中紅點處），這表明即使在大角度情況下密度參數仍然難以準確反演。不同參數之間的特征值差異隨著最大入射角的增大而減小，對應的反演條件數隨最大入射角的增大而減小，但在最大角度為50° 時，反演條件數仍然較高（大于20 dB），這表明PP 波三參數反演具有較高的病態性，尤其是難以準確反演密度參數。

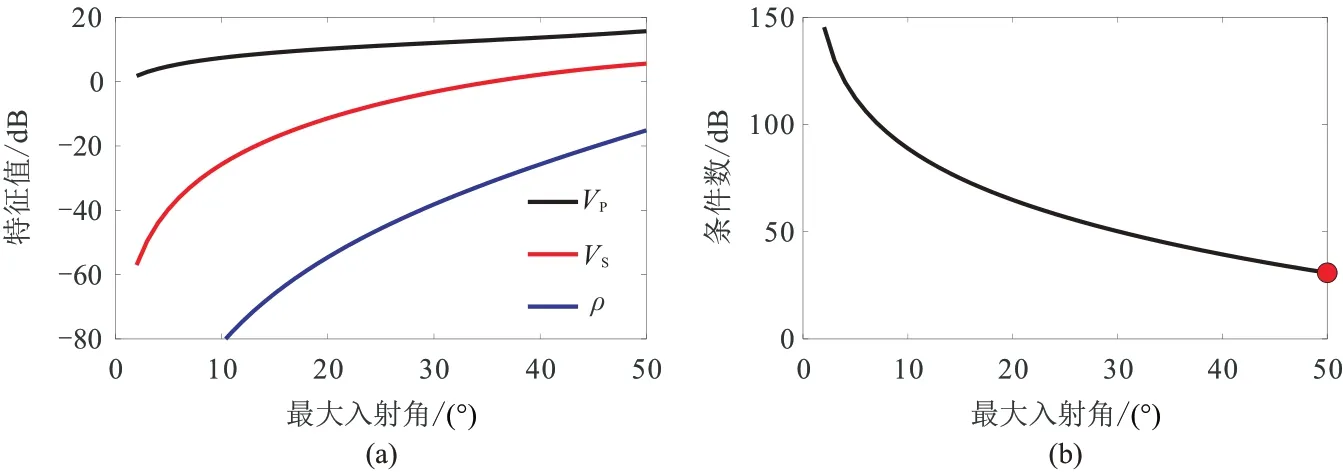
圖12 PP 波反演的特征值（a）和條件數（b）隨最大入射角的變化關系

4.2.2 PSV 波

PSV 波反演的特征值及條件數隨最大入射角的變化情況如圖13 所示，PSV 波反演僅有2 個待反演參數，其中VS特征值較大，表示VS對應的能量分量最大；而ρ特征值較小，隨著最大入射角的增大，ρ特征值逐漸增大，并且在最大入射角為48° 左右時，ρ特征值與VS特征值之差下降到20 dB 左右（圖中紅點處），表明此時可以得到密度參數可靠反演結果。相比于PP 波三參數反演，PSV 波反演的條件數有所下降，在最大入射角為48° 時下降到20 dB 左右，表示PSV 波反演可在一定程度上降低反演的不適定性，但仍需45° 以上的中角度數據才可得到可靠的密度反演結果。

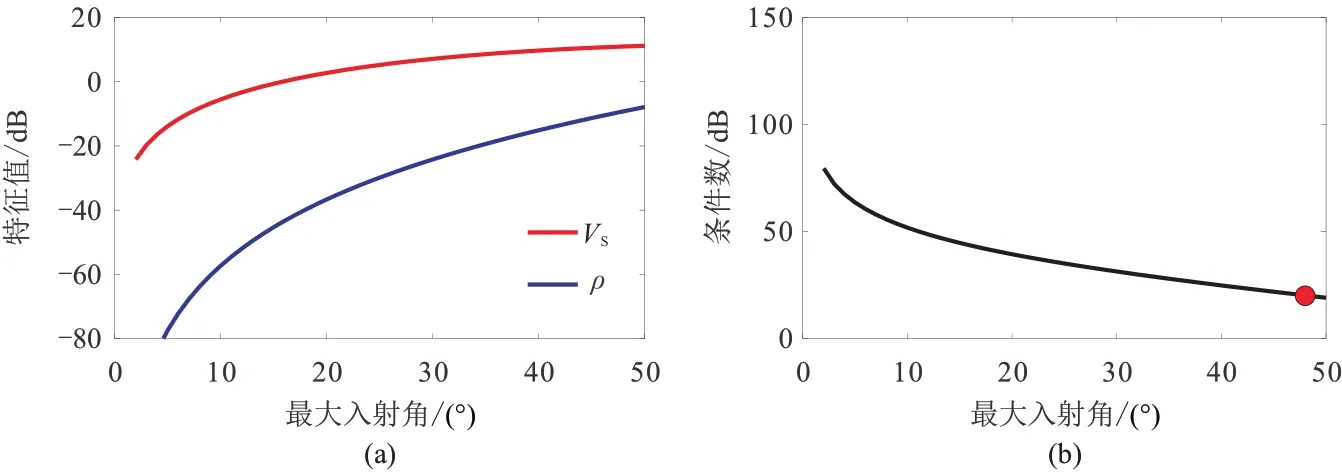
圖13 PSV 波反演的特征值（a）和條件數（b）隨最大入射角的變化關系

4.2.3 PP 波和PSV 波聯合反演

PP波和PSV 波聯合反演的特征值及條件數隨最大入射角的變化情況如圖14 所示。由圖可見，在三個特征值中VP特征值最大，表示VP對應的能量分量最大；而ρ特征值相比于PP 波反演明顯增大，表示ρ對應的能量分量得到提高，因此ρ反演的穩定性得到顯著提升。VP與ρ之間的特征值差異隨著最大入射角的增大而減小，對應的反演條件數隨最大入射角的增大而減小，這表明反演的病態性逐漸減弱。在最大入射角為20° 左右時，反演條件數下降到20 dB 左右（圖中紅點處），表明相比于PP 波三參數反演，PP 波和PSV 波聯合反演可顯著降低反演的不適定性，僅需20°左右的小角度數據即可準確反演密度參數。聯合反演可有效提高反演的穩定性，但在實際應用中需要考慮縱、橫波匹配精度的影響。

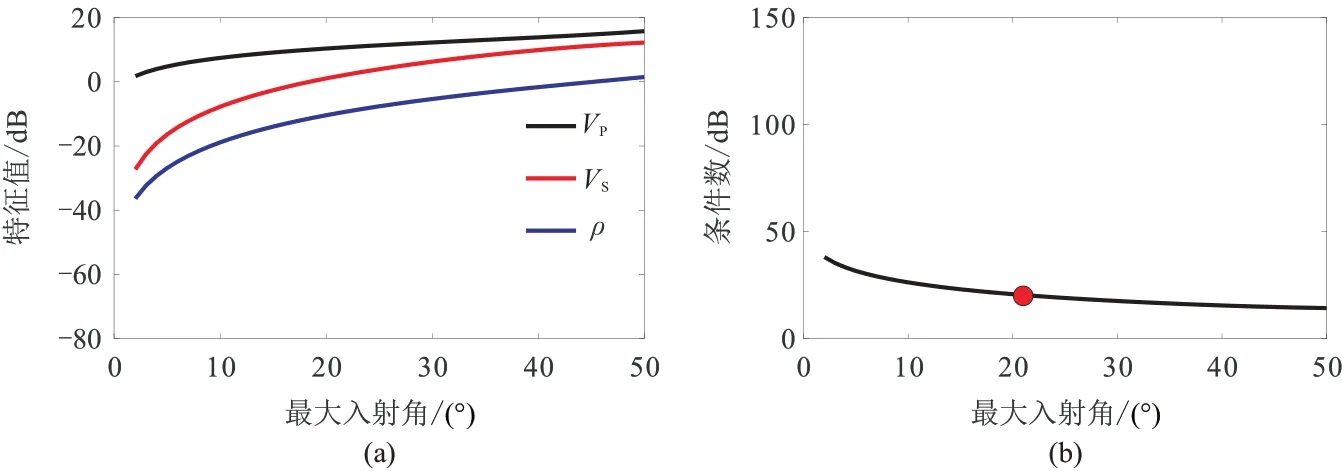
圖14 PP 波和PSV 波聯合反演的特征值（a）和條件數（b）隨最大入射角的變化關系

4.2.4 SH-SH 波

SH-SH 反演的特征值及條件數隨最大入射角的變化情況如圖15 所示。與PSV 波類似，SH-SH 波反演僅有2 個待反演參數，其中VS特征值較大，并且一直大于0，表示VS對應的能量分量最大；而ρ特征值較小，隨著最大入射角的增大，ρ特征值逐漸增大。在最大入射角為35°時，兩者特征值之差下降至20 dB 左右（圖中紅點處），表明ρ的可靠反演僅需35°左右的中角度數據即可。相比于PP 波三參數反演，SH-SH 波反演的條件數大幅下降，表示SH-SH 波反演可有效降低反演的不適定性，在密度反演方面具有較好的應用潛力。

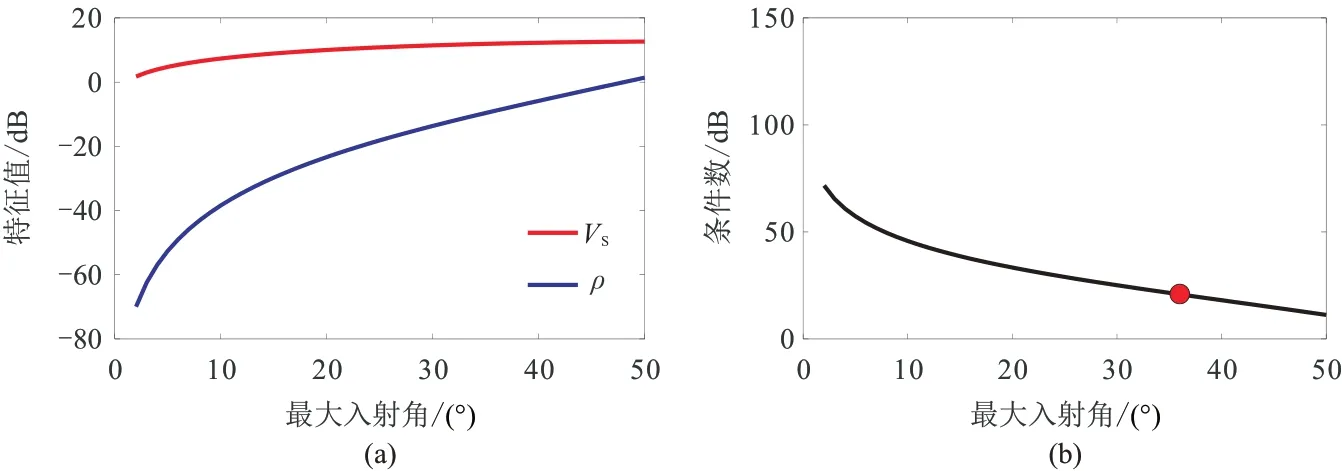
圖15 SH-SH 波反演的特征值（a）和條件數（b）隨最大入射角的變化關系

4.2.5 SV-SV 波

SV-SV 波反演的特征值及條件數隨最大入射角的變化情況如圖16 所示。SV-SV 波反演僅有2 個待反演參數，其中VS特征值隨最大入射角變化較小，但數值一直大于0，說明VS對應的大部分反射波能量分量；而ρ特征值隨著最大入射角的增大也明顯增大。兩者特征值之差在最大入射角為20°左右達到20 dB左右（圖中紅點處），表明ρ的可靠反演僅需20°左右的小角度數據即可。相比于PP 波三參數反演，SV-SV波反演的條件數大幅下降，表明SV-SV 波兩參數反演具有較低的不適定性，在密度反演方面具有顯著優勢。

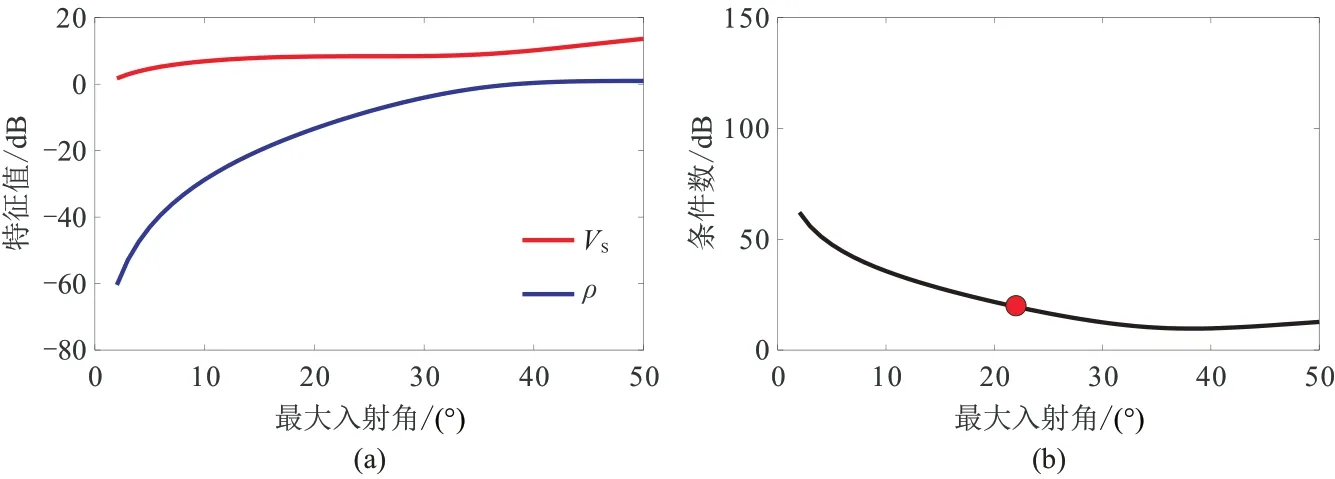
圖16 SV-SV 波反演的特征值（a）和條件數（b）隨最大入射角的變化關系

5 結果

綜上所述，根據反演協方差矩陣和反演條件數可得到不同類型地震波反演彈性參數的反演能力如表2所示。從表中可以看出，橫波（SV-SV 波和SH-SH波）在反演等橫波阻抗IS、橫波速度VS、剪切模量μ、密度ρ等參數時較縱波和轉換橫波有明顯的優勢，有效降低了反演對輸入數據的需求，并且顯著降低了反演的不適定性。

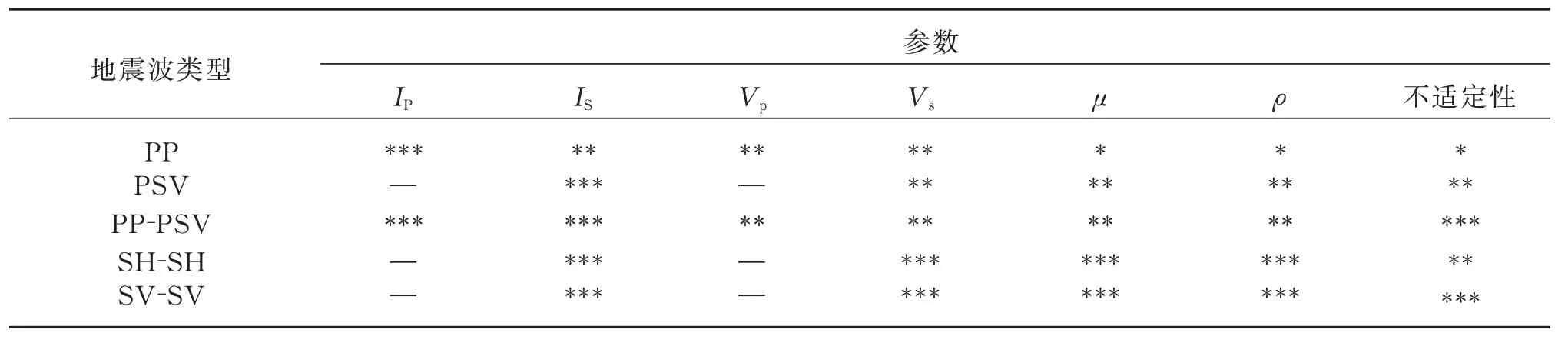
表2 不同類型地震波反演彈性參數時的可行性分析

6 結論與討論

本文基于不同類型地震波反射系數近似式，構建線性反演框架，利用反演協方差矩陣和反演條件數對比、分析了地震縱、橫波對不同彈性參數的反演能力。理論分析驗證了橫波在反演密度、剪切模量、橫波速度等參數方面具有良好的應用潛力，可為橫波反演方法研究提供有力的理論支撐。與轉換橫波相比，橫波的處理過程更為簡單，在彈性參數反演及儲層預測方面具有良好的應用前景。

需要說明的是，以上理論分析并沒有引入正則化，這是因為不同的正則化方法會不同程度地降低反演結果的不確定性和不適定性，不利于客觀地分析不同類型地震波的反演能力。而在實際地震數據反演中，則需要合理使用正則化以降低反演結果的不確定性。另外，在分析中假設不同類型的地震波數據具有相同的信噪比，這一假設可能與應用中的實際情況并不一致。

附錄A 不同類型地震波的線性正演算子F 表達式

根據P P波反射系數近似式（1），待求解參數為縱波速度VP、橫波速度VS和密度ρ時，入射角度分別為θ1，θ2，…，θN（N為角度個數），P P波線性正演算子F可表示為

式中γ為縱橫波速度比。

根據PSV 波反射系數近似式（式（4）），待求解參數為Vs 和ρ時，入射角度分別為θ1，θ2，…，θN，對應的SV 波反射角度為?1，?2，…，?N，F可表示為

根據SH-SH 波反射系數近似式（9），待求解參數為Vs 和ρ時，SH 波入射角度分別為?1，?2，…，?N，F可表示為

根據SV-SV 波反射系數近似式（式（12）），待求解參數為Vs 和ρ時，SV 波入射角和透射角的平均值分別為可表示為

當待求解參數為其他彈性參數時，根據不同類型地震波的反射系數近似式即可得到對應的F的表達式。