基于自適應增量Kriging模型的多目標穩健優化設計方法

田宗睿　智鵬鵬　云國麗　郭新凱　官毅

摘要：提出了一種自適應增量Kriging模型的多目標穩健優化設計方法。依據結構特征及優化目標，構建了增量Kriging代理模型，并提出混合加點采樣策略，提高增量Kriging代理模型的自適應性；提出了柯西變異多目標粒子群優化（CMMOPSO）算法，通過改進慣性權重因子、個體學習因子和社會學習因子，同時引入柯西變異策略，提高優化模型求解的效率和精度；構建以結構相關參數為設計變量、性能指標標準差為目標、3σ變量縮減區間為約束的優化模型，綜合CMMOPSO算法和灰色關聯分析獲得多目標穩健優化最優解。算例分析結果表明，所提方法不僅能夠以較少的性能函數調用次數獲得高精度結構優化模型，而且優化結果與傳統方法相比，收斂速度更快、穩健性更好。

關鍵詞：增量Kriging代理模型；混合加點策略；多目標粒子群算法；多目標穩健優化設計

中圖分類號：U270

DOI：10.3969/j.issn.1004-132X.2023.08.007

Multi-objective Robust Optimization Design Method Based on Adaptive Incremental Kriging Model

TIAN Zongrui1，2 ZHI Pengpeng1，4，5 YUN Guoli GUO Xinkai4 GUAN Yi5

Abstract： A multi-objective robust optimization design method of adaptive incremental Kriging model was proposed. Firstly， according to the structural characteristics and optimization objectives， the incremental Kriging surrogate model was constructed， and a hybrid sampling strategy was proposed to improve the adaptability of the incremental Kriging surrogate model. Secondly， the Cauchy mutation MOPSO（CMMOPSO） algorithm was proposed. By improving the inertia weight factor， individual learning factor and social learning factor， and introducing the Cauchy mutation strategy， the efficiency and precision of the optimization model were improved. Finally， an optimization model was constructed with the structural parameters as the design variables， the standard deviation of the performance indicators as the objective， and the 3σ variable reduction interval as the constraint. The optimal solutions of multi-objective robust optimization were obtained combining CMMOPSO and grey correlation analysis. Analysis results of the example show that the proposed method may obtain a high-precision structural optimization model with fewer performance function calls， and the optimization results have faster convergence rate and better robustness than that of traditional methods.

Key words： incremental Kriging surrogate model; mixed point strategy; multi-objective particle swarm optimization（MOPSO） algorithm; multi-objective robust optimization design

0 引言

傳統的穩健優化方法包括：田口穩健優化、基于容差模型的穩健優化、基于隨機模型的穩健優化方法等。由于這些方法屬于數值方法，不適用于實際工程中需要大規模不確定性分析的黑箱函數問題，因此發展高效且適用范圍廣的穩健優化方法迫在眉睫。

目前相對有效的方法是基于代理模型的穩健優化方法，國內外眾多學者對此進行了研究。LUO等［1］將代理輔助梯度方法應用于渦輪機葉片氣動穩健優化中。RAFIEE等［2］使用Box-Behnken響應面法的十維代理模型與粒子群優化相結合，完成外轉子永磁電機的穩健設計。TAO等［3］將PCA-DBN代理模型嵌入改進的粒子群優化框架中，并將其應用于自然層流翼型和跨音速機翼的穩健氣動設計優化。LIU等［4］利用Kriging模型和田口法對懸掛式單軌車輛參數進行穩健優化。劉太素等［5］基于稀疏混沌多項式展開模型進行了輸彈協調機構的穩健優化設計。萬良琪等［6］針對復雜裝備精密產品提出一種基于多項式混沌擴展的6σ穩健優化設計方法。向國齊等［7］提出一種基于支持向量機和粒子群算法結合的穩健優化方法。上述學者對穩健優化的研究過程主要采用“代理模型+智能進化算法”的邏輯結構，雖然得到了令人滿意的結果，但均是在大量仿真試驗的基礎上展開研究的，未充分利用代理模型的優勢，也忽略了求解精度和求解效率。

利用Kriging模型進行穩健優化設計是解決上述問題的有效途徑。通過序貫Kriging采樣方法，可有效處理穩健優化目標的不確定性，也能避免傳統靜態Kriging模型一次采樣產生低精度預測的缺點。針對單點加點準則，XIAO等［8］提出了加權期望提高準則（weighted expected improvement， WEI），并應用在電磁設計中。AMINE等［9］在期望提高準則（expected improvement， EI）的基礎上提出了WB2準則，增強了局部搜索能力。王彥等［10］提出了nEI準則，與EI準則相比，可得到更高精度的模型，但犧牲了迭代速度。

上述學者對單點加點準則展開了研究，但是能夠提高采樣效率的多點加點策略能與并行計算相結合，在近年來受到了更廣泛的關注。針對多點加點準則，ZHAN等［11］提出偽期望改進準則，通過建立影響函數進行多點加點。LI等［12］開發了一種名為期望提高和交互信息（expected improvement and mutual information， EI&MI）的多點填充準則。陳鵬等［13］結合最小響應面準則（minimizing prediction， MP）和EI準則，提出了一種雙加點動態Kriging模型。樂春宇等［14］利用EI和WB2準則設計了兩階段并行采樣策略。謝延敏等［15］通過并行使用EI準則，在迭代過程中能夠增加兩個采樣點，有效提高了模型的擬合精度。上述研究均提高了黑箱函數的局部精度和最優點附件的精度，但是在穩健優化設計中仍需考慮設計域全局精度的擬合效果。

針對上述問題，為獲得高質量的黑箱函數擬合樣本，兼顧多目標穩健優化設計的求解精度和效率，本文提出一種基于自適應Kriging模型的多目標穩健優化設計方法。與現有方法相比，通過融合EI準則、MP準則和最大方差準則（maximizing square error， MSE）的采樣特性，提出了自適應增量Kriging代理模型的并行加點方法；在此基礎上，提出了能夠高效解決多目標穩健優化問題的柯西變異多目標粒子群優化

（Cauchy mutation multiple objective particle swarm optimization，CMMOPSO）算法；通過數值算例和工程算例進行了驗證。

1 自適應增量Kriging模型

在實際工程中，結構性能的評估指標通常利用仿真過程實現，但是過多的仿真計算不但會增加計算成本，也會降低分析過程的計算速度。因此，針對穩健優化過程，在增量Kriging模型的基礎上，通過引入自適應混合加點策略，考慮距離閾值的樣本刪除策略和自適應收斂準則，提出一種能夠高效擬合結構性能指標的自適應增量Kriging模型。

1.1 增量Kriging模型基本原理

增量Kriging模型［16］可看成是在普通Kriging模型的基礎上進行了理論拓展。與普通Kriging模型相比，增量Kriging模型能夠避免相關函數矩陣求逆耗時的弊端，在模型每次更新時不需要重新計算，能夠有效提高Kriging模型的建模效率。

（1）根據工程要求，確定結構性能的多個評估指標，以及穩健優化的設計變量x=（x1，x2，…，xM）T和設計空間（xL，xU）。

（2）對設計變量x=（x1，x2，…，xM）T進行拉丁超立方抽樣，通過仿真分析輸出性能評估指標真實響應值y=（y1，y2，…，yM）T，建立初始增量Kriging模型。

（3）根據混合加點策略，更新Kriging模型。通過迭代加點，基于當前樣本庫建立增量Kriging模型，同時將更新點加入樣本庫。每完成一次迭代，迭代次數增加1，即k←k+1，當RMSE值滿足eRMSE≤ε（其中ε為精度閾值）時停止加點，進行步驟（4）；否則返回步驟（3）。

（4）建立性能評估指標的Kriging代理模型。通過對設計變量x′=（x′1，x′2，…，x′M）T進行拉丁超立方抽樣，獲得性能評估指標的預測樣本y′=（y′1，y′2，…，y′M）T。

（5）對每組拉丁超立方抽樣樣本進行蒙特卡羅抽樣，獲得性能評估指標的標準差σMC=（σ1，σ2，…，σM），并建立性能評估指標的標準差Kriging代理模型。

（6）以性能評估指標的標準差為優化目標，以基于3σ準則的縮減區間為約束條件，建立多目標穩健優化模型。

（7）利用CMMOPSO算法計算多目標穩健優化模型，輸出帕累托解集。

（8）根據灰色關聯分析篩選出最優帕累托最優解。

（9）輸出最優穩健優化結果。

5 方法驗證及工程應用

5.1 自適應增量Kriging模型有效性驗證

為進一步確定混合加點準則的合理性，選擇經典的EI、EI+MP、Kriging believer（KB）方法［18］進行對比。其中EI方法進行單點加點，EI+MP方法進行雙點加點，KB方法和本文方法進行四點加點。選擇six-hump camel-back（SC）函數算例進行方法驗證，其函數圖像如圖2所示。

由圖2所示，SC函數是一個高度非線性函數，能夠有效驗證混合加點策略的應用可行性和廣泛性，具體表達式為

在本算例中，設置初始擬合樣本量為20，當eRMSE＜0.01時，停止迭代。

利用拉丁超立方抽樣隨機生成50個樣本點作為Kriging模型精度驗證的測試樣本，具體數據見表1。

利用表1中的50組測試樣本計算Kriging模型的RMSE，其值隨加點迭代過程的變化如圖3所示。由圖3可知，本文方法在第16次迭代時達到收斂條件，而KB和EI+MP方法分別需要20和54次；EI+MP方法迭代次數最多，當迭代次數為70時RMSE仍未收斂到0.01，這是由于該方法只關注了局部和全局極小值處的精度，忽略了極大值和不確定樣本的影響。由此可知，所提方法在迭代次數方面表現出了顯著優勢。

加點總樣本數對迭代次數的變化過程如圖4所示。由圖4可知，在保證初始擬合樣本數目相同的條件下，本文方法的迭代次數為16時總樣本數為58，與EI方法相比減少了20.55%，與KB方法相比減少了32.56%。EI+MP方法所需樣本數最多，當迭代次數為70時總樣本數為157。結果表明本文方法能夠調用最少的仿真次數，降低計算成本。

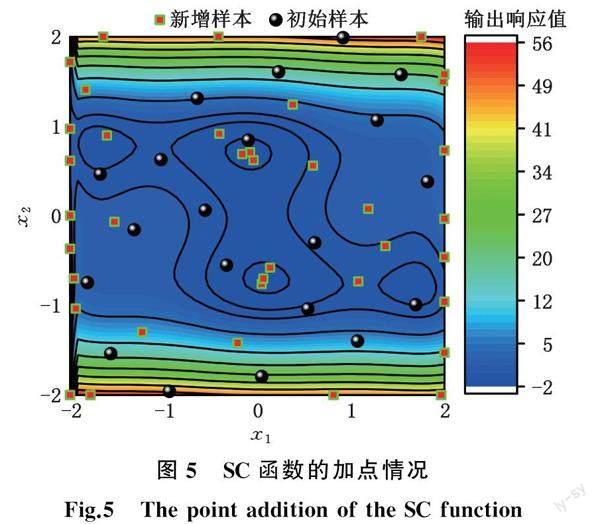
本文方法擬合函數在等高線圖中的加點情況如圖5所示。由圖5可知，拉丁超立方抽樣生成的初始擬合樣本分布均勻性和隨機性較好。所提方法的新增樣本不僅在函數的取值邊界處和極值處采樣，在函數等高線圖的山谷、山峰和山脊處也能夠兼顧采樣，表明所提方法能夠考慮非線性函數全局空間的所有特征，具有良好的可行性和應用價值。

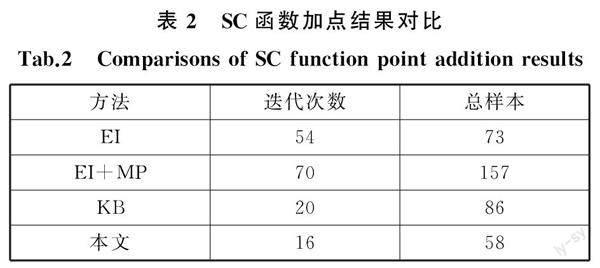
4種方法的對比結果見表2。由表2可知，與EI、EI+MP、KB方法相比，本文方法在迭代次數和調用仿真獲得的總樣本數方面均表現出不俗的優勢。由此可知，本文方法可在一次迭代中增加多個點，提高了代理模型的擬合效率，同時由總樣本數可知，本文方法能夠明顯減少仿真次數，具有良好的經濟效益。

5.2 動車組制動模塊多目標穩健優化

制動模塊作為動車組制動系統的重要組成部分，會承擔各種形式的載荷，從而引起列車的多種失效形式，所以對制動模塊進行性能仿真優化具有重要意義。首先，利用HyperMesh軟件建立制動模塊有限元模型，單元類型主要包括SHELL181、MASS21和BEAM188。其中SHELL181包括四節點四邊形單元和三角形三節點單元，網格大小約為10 mm。有限元模型共包含49 868個節點和48 057個單元。模型性能分析屬于靜強度分析范疇，在4個制動吊座處分別施加X/Y/Z方向、X/Y方向、Y/Z方向和Z方向的位移約束，制動模塊有限元模型如圖6所示。

根據BS EN12663—2010《鐵路應用車輛車身的結構要求》［19］標準，確定制動模塊的超載工況見表3。選擇工況1作為穩健優化的基礎。利用ANSYS對工況1進行靜強度仿真分析，得到的應力云圖見圖7。由圖7可知，動車組制動模塊的結構應力最大值為223.254 MPa，發生在支撐架外側橫向梁和內側縱向梁的連接處，該處的許用應力最大值為235 MPa，滿足要求。但是，由于制動模塊在設計和使用過程中容易受到不確定因素的影響，容易超過安全余量，因此該模型仍有優化空間。考慮制動模塊結構設計過程中板厚的不確定性，借助ANSYS和MATLAB對其進行穩健優化。

首先，根據穩健優化流程，選擇不同結構的板厚作為隨機變量，各變量的分布特征見表4。

其次，選擇制動模塊的應力和質量作為性能評估指標。利用拉丁超立方抽樣方法建立應力和質量的增量Kriging模型。確定應力和質量的初始擬合樣本量分別為20和10，測試樣本量為10，通過有限元分析獲得真實輸出響應值。當eRMSE＜0.1時，停止加點。

通過混合加點準則，獲得應力迭代曲線見圖8，質量迭代曲線見圖9。由圖8可知，對于應力Kriging模型，本文方法收斂速度最快，迭代17次即可達到應力精度要求，EI方法最多需要迭代139次達到精度要求。由圖9可知，對于質量Kriging模型，本文方法收斂速度最快，迭代9次即可達到應力精度要求，EI方法最多需要迭代66次達到精度要求。

將所有算法的計算結果進行對比，具體見表5。由表5可知，對應力進行Kriging代理模型擬合時，本文方法的迭代次數最少為17次，通過仿真獲得的樣本點數最少為65個，所用時間僅為87.68 s。對質量進行Kriging代理模型擬合時，本文方法的迭代次數最少為9次，通過仿真獲得的樣本點數最少為33個，所用時間僅為45.91 s，表明建立的混合加點增量Kriging能夠通過更少的樣本點獲得所需的模型精度。

根據圖1所示的穩健優化流程圖，對制動模塊的應力和質量進行穩健優化。建立穩健優化數學模型表達式：

式中，σs為應力s的標準差；σm為質量m的標準差；XRi為相應變量的標準差，其中XRi=0.03μXi，μXi為各變量的均值。

利用CMMOPSO算法對確定性和穩健性優化數學模型進行計算，得到確定性優化的帕累托解集如圖10所示，穩健性優化的帕累托解集如圖11所示。由圖10可知，與MOPSO算法得到的帕累托解集相比，CMMOPSO算法得到的帕累托解集的分布具有均勻性和廣泛性，應力值在［250，350］區間時，CMMOPSO算法得到的解集能夠支配MOPSO算法得到的解集，表明算法收斂性更強。由圖11可知，當σs在［2，6］區間時，CMMOPSO算法得到的解集在均勻性、收斂性和廣泛性方面均表現出較強的優勢，表明CMMOPSO算法輸出的帕累托解對制動模塊的穩健優化具有工程價值和參考意義。

通過計算帕累托解集的灰色關聯度，評估帕累托解的優劣。選擇灰色關聯度最大的帕累托解作為最佳多目標優化解。確定性優化和穩健性優化帕累托解集的灰色關聯度結果如圖12所示。根據圖12中輸出的確定性優化和穩健性優化的最優解，將其代入Kriging模型中計算，最終優化結果對比見表6。由表6可知，與原始方案相比，確定性和穩健性優化后的應力和質量均有所減小，表明確定性和穩健性優化效果良好。與確定性優化相比，穩健性優化得到的應力均值減小了3.16%，質量均值增大了6.54%，應力標準差減小了27.84%，質量標準差減小了15.12%。綜上所述，穩健性優化明顯減小了應力和質量的標準差，減小了制動模塊產品的性能波動，提高了產品質量特性，證明了所提混合加點增量Kriging模型的多目標穩健優化設計方法的有效性。

6 結論

（1）本文提出自適應增量Kriging模型的建立方法，克服了傳統一次建模精度低的缺點。結果表明：所提方法能夠有效提高模型精度，同時減少模型所需樣本點數量，降低了模型創建成本。

（2）提出CMMOPSO算法，解決了原始MOPSO算法收斂效率低和易陷入局部最優解的缺點。結果表明：改進算法所得帕累托解集的收斂性、均勻性和廣泛性均有所改善，提高了算法的綜合計算性能。

（3）數值和工程結果表明：利用自適應增量Kriging模型能夠高效建立復雜非線性黑箱函數的代理模型；采用CMMOPSO算法進行穩健優化能夠得到均勻性和廣泛性更佳的帕累托解集。穩健優化后制動模塊的質量波動減小，結構穩健性提高，進一步證明了方法的高效性，對機械結構的改進及優化具有重要的工程意義和研究價值。

參考文獻：

［1］LUO J Q， CHEN Z H， ZHENG Y. A Gradient-based Method Assisted by Surrogate Model for Robust Optimization of Turbomachinery Blades［J］. Chinese Journal of Aeronautics， 2022，35（10）：1-7.

［2］RAFIEE V， FAIZ J. Robust Design of an Outer Rotor Permanent Magnet Motor through Six-sigma Methodology Using Response Surface Surrogate Model［J］. IEEE Transactions on Magnetics， 2019， 55（10）：1-10.

［3］TAO J， SUN G， GUO L Q， et al. Application of a PCA-DBN-based Surrogate Model to Robust Aerodynamic Design Optimization［J］. Chinese Journal of Aeronautics， 2020， 33（6）：1573-1588.

［4］LIU W， YANG Y， ZHENG R， et al. Robust Optimization for Suspension Parameters of Suspended Monorail Vehicle Using Taguchi Method and Kriging Surrogate Model［J］. Journal of the Chinese Society of Mechanical Engineers， Transactions of the Chinese Institute of Engineers—Series C， 2019， 40（5）：481-489.

［5］劉太素， 錢林方， 陳光宋， 等. 基于SPCE-HDMR的某輸彈協調機構穩健設計研究［J］. 彈道學報， 2019， 31（4）：90-96.

LIU Taisu， QIAN Linfang， CHEN Guangsong， et al. Research on Robust Design of a Ammunition Coordination Mechanism Based on SPCE-HDMR［J］. Journal of Ballistics， 2019， 31（4）：90-96.

［6］萬良琪， 陳洪轉， 歐陽林寒， 等. 復雜裝備精密產品多項式混沌擴展穩健優化設計［J］. 計算機集成制造系統， 2018， 24（5）：1240-1248.

WAN Liangqi， CHEN Hongzhuan， OUYANG Linhan， et al. Robust Optimization Design of Polynomial Chaos Expansion for Complex Equipment and Precision Products［J］. Computer Integrated Manufacturing Systems， 2018， 24（5）：1240-1248.

［7］向國齊， 殷國富. 基于支持向量機和粒子群算法的穩健優化［J］. 機械設計與研究， 2016， 32（6）：6-9.

XIANG Guoqi， YIN Guofu. Robust Optimization Based on Support Vector Machine and Particle Swarm Optimization［J］. Mechanical Design and Research， 2016， 32（6）：6-9.

［8］XIAO S， ROTARU M， SYKULSKI J K. Exploration Versus Exploitation Using Kriging Surrogate Modeling in Electromagnetic Design［J］. COMPEL—The International Journal for Computation and Mathematics in Electrical and Electronic Enginee-ring， 2012， 31（5）：1541-1551.

［9］AMINE B M， BARTOLI N， REGIS R G， et al. Efficient Global Optimization for High-dimensional Constrained Problems by Using the Kriging Models Combined with the Partial Least Squares Method［J］. Engineering Optimization， 2018， 50（12）：2038-2053.

［10］王彥， 尹素菊. 基于改進EGO算法的黑箱函數全局最優化［J］. 計算機應用研究， 2015， 32（3）：764-767.

WANG Yan， YIN Suju. Global Optimization of Black Box Function Based on Improved EGO Algorithm［J］. Computer Application Research， 2015， 32（3）：764-767.

［11］ZHAN D， QIAN J， CHENG Y. Pseudo Expected Improvement Criterion for Parallel EGO Algorithm［J］. Journal of Global Optimization， 2017， 68（3）：641-662.

［12］LI Z， RUAN S， GU J， et al. Investigation on Parallel Algorithms in Efficient Global Optimization Based on Multiple Points Infill Criterion and Domain Decomposition［J］. Structural and Multidisciplinary Optimization， 2016， 54（4）：747-773.

［13］陳鵬， 章青， 黃磊. 基于雙加點動態Kriging模型的提升塔架優化設計［J］. 中國機械工程， 2019， 30（19）：2335-2341.

CHEN Peng， ZHANG Qing， HUANG Lei. Optimal Design of Lifting Tower Based on Double-point Dynamic Kriging Model ［J］. China Mechanical Engineering， 2019， 30（19）：2335-2341.

［14］樂春宇， 馬義中. 基于Kriging模型的自適應多階段并行代理優化算法［J］. 計算機集成制造系統， 2021， 27（11）：3227-3235.

YUE Chunyu， MA Yizhong. Adaptive Multi-stage Parallel Agent Optimization Algorithm Based on Kriging Model［J］. Computer Integrated Manufacturing System， 2021， 27（11）：3227-3235.

［15］謝延敏， 張飛， 潘貝貝， 等. 基于并行加點kriging模型的拉延筋優化［J］. 機械工程學報， 2019， 55（8）：73-79.

XIE Yanmin， ZHANG Fei， PAN Beibei， et al. Optimization of Drawbead Based on Parallel Adding Kriging Model［J］. Journal of Mechanical Engineering， 2019， 55（8）：73-79.

［16］ZHAN D， XING H. A Fast Kriging-assisted Evolutionary Algorithm Based on Incremental Learning［J］. IEEE Transactions on Evolutionary Computation， 2021， 25（5）：941-955.

［17］COELLO C A C， LECHUGA M S. MOPSO：a Proposal for Multiple Objective Particle Swarm Optimization［C］∥Proceedings of the 2002 Congress on Evolutionary Computation. Honolulu， 2002：1051-1056.

［18］GINSBOURGER D， RICHE R L， CARRARO L. Kriging Is Well-suited to Parallelize Optimization［J］. Adaptation Learning and Optimization， 2010， 2：131-162.

［19］British Standard Institute. Railway Applications Structural Requirements of Railway Vehicle Bodies：BS EN12663-1—2010［S］. London：BSI， 2010.

（編輯 王旻玥）

作者簡介：

田宗睿，男，1997年生，碩士研究生。研究方向為基于代理模型的優化設計與可靠性分析方法。E-mail：tianzongrui9731@163.com。

智鵬鵬（通信作者），男，1989年生，博士、助理研究員。E-mail：zhipeng17@yeah.net。

收稿日期：2022-08-08

基金項目：廣東省基礎與應用基礎研究基金（2021A1515110308）；四川省自然科學基金（2022NSFSC1941）