基于城市標度律模型的不同規模城市發展指標研究

李薇宇，賀 曉，李文皓，孫名揚，范宇瓊

（蘇州科技大學 數學科學學院，江蘇 蘇州 215009）

改革開放以來，中國的各個城市基本上得到了快速的發展，城市經濟呈現上升趨勢[1]。然而，隨著城市化的快速發展，中國的城市內部也出現了一些問題，如人口數量激增、就業壓力大、資源短缺、生態環境惡化等。區域之間也出現了發展不平衡狀況，呈現特大城市群持續擴張，中小城市發展緩慢，城市之間與城鄉之間貧富差距擴大趨勢[2]。傳統研究城市發展的理論并不能很好地適應當下的中國城市發展的狀況[3-4]，因此，需要更好的模型來研究較為復雜的城市系統。標度律（Scaling Law）便是研究城市系統復雜性的理論之一，它是指某種指標在不同情況下所滿足的統一規律[5]，如常見的冪律就是標度律的一種形式。大量研究表明，標度律是物理學、生物學、化學等復雜系統中存在的普遍規律。例如，在生物學上，生物的新陳代謝頻率與個體尺寸的異速增長關系與標度律有關[6]，研究者發現，將不同物種的新陳代謝頻率與生物體的體積畫到對數坐標上，所有哺乳動物基本上落在一條斜率為0.75 的直線上，這個關系式揭示了生物能量消耗的規模效應，即質量越大的組織，單位質量單位時間的能耗更低[7]。而后研究者將標度律引入到城市科學[8]、空間科學領域[9]，在不斷完善和改進過程中，建立了城市標度律的整體框架。

城市標度律的冪函數形式為Y（t）=Y0N（t）β[10]，其中，Y（t）為t 時刻城市的指標，可以指物質方面的資源（例如基礎設施數量、建成區面積），或者為社會活動的度量（例如GDP、煙塵排放量等）；Y0是一個標準化的常量；N（t）代表t 時刻的城市人口規模；β 為標度因子。在城市體系內，城市標度律可以系統化展示某種城市指標與人口規模的冪律關系，在選取了不同的指標后，可以發現和分析整個城市體系的狀態和特征。

目前國內學者對于城市標度律的研究處于初始階段[11-14]，應用層面較少，對城市標度律的理論研究不夠深入，并存在一些誤解。因此，文中立足于我國目前的城市經濟背景與城市可持續發展的政策要求，綜合考慮我國目前不同規模城市發展的情況，圍繞影響城市發展的因素，主要針對以下兩方面進行實證研究：（1）借助城市標度律探討不同城市規模下中國城市綜合發展狀況，在此基礎上進行城市發展指標和影響因素分析，試圖為城市可持續發展提供思路；（2）用數據來驗證城市標度律的適用性，尋找城市標度律的內在邏輯，并借助修正模型來提高城市標度律的準確性和穩定性。

該論文創新點有三：第一，用較為新穎的城市標度律模型代替傳統的城市發展理論來量化城市發展水平指標；第二，利用分形理論，依據人口規模將城市分為三個類別進行研究；第三，利用折線擬合代替直線擬合來提高擬合優度，處理存在異質性的數據。

通過筆者的研究，借助城市標度律量化模型，構建衡量城市發展水平的指標，不僅可以有效評估我國當前城市的發展水平，還在此基礎上分析不同城市規模下城市發展的差異性，結合城市發展模式，從多維度發掘城市發展的內核動力。因此，一方面，論文的研究有利于政府選擇合適的指標來衡量城市發展狀況；另一方面，論文的研究有利于合理規劃不同城市規模的發展方向。

1 數據與區域劃分

文中以中國各城市為研究對象，收集整理了2018 年294 個地級市的城區常住人口、工業廢水排放量（Industrial Wastewater Discharge，簡稱IWD，單位：t）、市轄區建成區面積（Area of Built-up Areas under Municipal Jurisdiction，簡稱BUA，單位：km2）、第一產業GDP（簡稱1GDP，單位：元）、第二產業GDP（簡稱2GDP，單位：元）、第三產業GDP（簡稱3GDP，單位：元）數據[15]，其中常住人口為城區的戶籍人口和暫住人口之和，數據均來自于2018《中國城市統計年鑒》。依據《中國城市規模劃分新標準的適用性研究》，采用第六次人口普查數據將中國城市劃分為三類：城區常住人口100 萬以下的城市為小中城市；城區常住人口100 萬以上500 萬以下的城市為大城市；城區常住人口500 萬以上的城市為特大及以上城市。

2 模型的建立、求解與檢驗

2.1 建立模型

城市標度律通常為冪函數形式Y=Y0Nβ來表示[10]。文中將城市標度律模型優化為

其中，Y 為城市指標，可以表示資源水平（例如學校數量、醫院數量、市轄區建成區面積）或者對于經濟發展、工業發展的度量（例如GDP、硫化物排放量等）；k 為城市劃分標準中的第k 類城市，k=1，2，3；Y0k是一個標準化常量；N 代表t 時刻的城市的人口水平，用來衡量城市的規模；β 為標度因子，βk與1 的大小關系可以反映Y 與城市人口規模N 之間的關系，可將展現城市屬性的變量分為3 種類型[10]：

（1）超線性指標（βk＞1）：與社會交互相關的城市指標（如疾病、GDP、知識產出、違法犯罪等）的標度因子大于1（一般在1.15 左右），該類城市指標隨城市人口規模呈超線性增長，這是因為社會交互隨人口增加呈超線性增長，從小城市到大城市，要素增加率大于人口增長率，體現了規模報酬遞增效應（集聚效應）；

（2）次線性指標（βk＜1）：與城市基礎設施相關的城市指標（如學校數量、醫院數量等）的標度因子小于1（一般在0.85 左右），該類城市指標隨人口規模呈次線性增長，表明從小規模城市到大規模城市，要素增加率小于人口增加率，這是因為大城市有更多居民共享城市基礎設施，反映了規模經濟效應，例如盡管上海有4倍于南通的人口，但上海并不需要南通4 倍數量的加油站（加油站與人口的冪律指數為0.77）；

（3）線性指標（βk=1）：與城市居民個人需求相關的城市指標（如工作崗位數量、住房數量、家庭用水量等個體需求相關）的標度因子等于1，該類城市指標隨城市人口規模呈線性變化。

對城市標度律方程兩邊同時取對數后，采用最小二乘法（OLS）得到回歸檢驗方程[10，16]

式中：對于Y，文中分別統計和計算了代表城市經濟發展水平的GDP、工業廢水排放量、第一產業GDP、第二產業GDP、第三產業GDP，代表城市用地指標的市轄區建成區面積；N 是城市人口；logY0k是常數；βk作為回歸系數參數反映了城市系統中各指標的標度律。

考慮到統計數據質量可能會一定程度地影響實證結果，進行回歸分析時采用殘差平均值正負兩倍標準差剔除異常值。首先對人口及城市要素取對數進行線性回歸擬合，得到斜率βk及截距logY0k，并用實際值減去預期值得到殘差ξ

若logY 在殘差平均值正負兩倍標準差范圍外，則視其為異常值，予以剔除。剔除異常值后再根據保留的數據重新擬合，得到標度因子β 及擬合優度R2。

2.2 模型評價

該模型適用于國內大部分綜合發展型城市，但不適用于資源型城市。因為資源型城市的GDP 數據深受當地礦產資源的影響，不能作為城市發展水平的量化指標，但對于非資源型城市而言，GDP 可以體現當地的城市發展水平。

這里采用擬合優度（R2）和均方誤差根（RMSE）作為模型性能的評價指標，RMSE 和R2定義如下

其中，yi代表某一城市指標的真實值，代表擬合值，n 代表樣本個數。

2.3 規模修正指標

城市標度律是全球城市系統普遍表現出的規律[16-18]，探究其在城市研究中的具體應用是目前國內外大多數學者重點研究的問題。傳統做法上多采用人均指標衡量城市表現，但這忽略了城市指標與人口規模的非線性標度關系。為消除城市人口規模的影響，Bettencourt 等提出了規模修正指標SAMI[10]，其定義式如下

式中：SAMIi為消除規模影響的城市i 的某一指標，實質為城市指標關于人口規模擬合方程的殘差，表示偏離其預期值的程度；Yi為城市i 的某個指標的真實值；Y0Niβ為城市i 的某個指標的估計值；Ni為城市i 的常住人口規模；Y0和β 為擬合參數。

3 結果與分析

3.1 直線擬合

不同指標直線擬合圖，如圖1 所示。對各個指標進行對比分析發現，工業廢水排放量、第二產業GDP、第三產業GDP 和GDP 的β 估值均大于1，說明以上四個指標為超線性指標，體現了規模報酬遞增效應；而市轄區建成區面積和第一產業GDP 的β 估值均小于1，說明以上兩個指標為次線性指標，體現了分散效應。對于截距logY 的估值：第一產業GDP、第二產業GDP、第三產業GDP 和GDP 的logY 估值均為正值，說明以上四個指標中Y＞1，具有擴大作用；對而工業廢水排放量和市轄區建成區面積的logY 估值均為負值，說明以上兩個指標中0＜Y＜1，具有收縮作用。對于P 值：六個指標的P 值均小于2.2×10-16，即均小于0.001，故均在P=0.001 水平上通過了顯著性檢驗。在擬合優度R2方面：工業廢水排放量、市轄區建成區面積和第一產業GDP的R2均約等于0.4，說明以上三個指標擬合優度較差；而第二產業GDP、第三產業GDP 和GDP 的R2均大于6，說明以上三個指標擬合優度較好。

3.2 折線擬合

不同指標折線擬合結果，如圖2 所示。

對所選不同指標進行折線擬合后所得結果進行分析發現，以特大城市、大城市、小中城市的第一產業GDP 為例。對于小中城市的第一產業GDP 指標，截距（logY01）的估值、標準誤差、T 值、P 值分別為-1.420 8、3.397 3、-0.418、0.682 62；β 的估值、標準誤差、T 值、P 值分別為1.828 1、0.585 8、3.121、0.008 12，其中P=0.008 12＜0.01，通過顯著性檢驗；擬合優度為0.428 3，修正擬合優度為0.384 3，方程的擬合程度較好；對于F檢驗，其P 值為0.008 118，顯然小于0.01，該方程在P=0.01 水平上通過顯著性檢驗。對于大城市的第一產業GDP 指標，截距（logY02）的估值、標準誤差、T 值、P 值分別為3.873 7、0.994 9、3.893、0.000 139，其中P=0.000 139＜0.001，通過顯著性檢驗；β 的估值、標準誤差、T 值、P 值分別為0.916 8、0.154 6、5.929、1.54×10-8，其中P=1.54×10-8＜0.001，通過顯著性檢驗；擬合優度為0.164 1，修正擬合優度為0.159 5，方程的擬合程度一般；對于F 檢驗，其P 值為1.538×10-8，顯然小于0.001，該方程在P=0.001 水平上通過了顯著性檢驗。對于特大及以上城市的第一產業GDP 指標，截距（logY03）的估值、標準誤差、T 值、P 值分別為9.144 2、1.727 0、5.295、9.37×10-7，其中P=9.37×10-7＜0.001，通過顯著性檢驗；β 的估值、標準誤差、T 值、P 值分別為0.146 2、0.251 1、0.582、0.562；擬合優度為0.004 016，修正擬合優度為-0.007 841；對于F 檢驗，其P 值為0.562 1。對于其他五個指標折線擬合的結果解讀同上。

3.3 不同城市規模下各個指標的分析

下面分別對三種城市規模的各個指標進行分析（見表1）。以大城市為例，第二產業GDP、第三產業GDP、GDP、工業廢水排放量的β 估值均大于1，說明該指標為超線性指標，體現了規模報酬遞增效應；第一產業GDP、市轄區建成區面積的β 估值均小于1，說明以上指標為次線性指標，體現了分散效應。對于截距logY0的估值，工業廢水排放量和市轄區建成區面積的logY0估值均為負值，說明以上兩個指標中0＜Y＜1，具有收縮作用；第一產業GDP、第二產業GDP、第三產業GDP、GDP 的logY0估值均為正值，說明以上四個指標中Y＞1，具有擴大作用。第一產業GDP、第二產業GDP、第三產業GDP、GDP、工業廢水排放量、市轄區建成區面積的P 值均小于0.001，故均在P=0.001 水平上通過了顯著性檢驗。對于其他兩種城市規模的結果解讀同上。

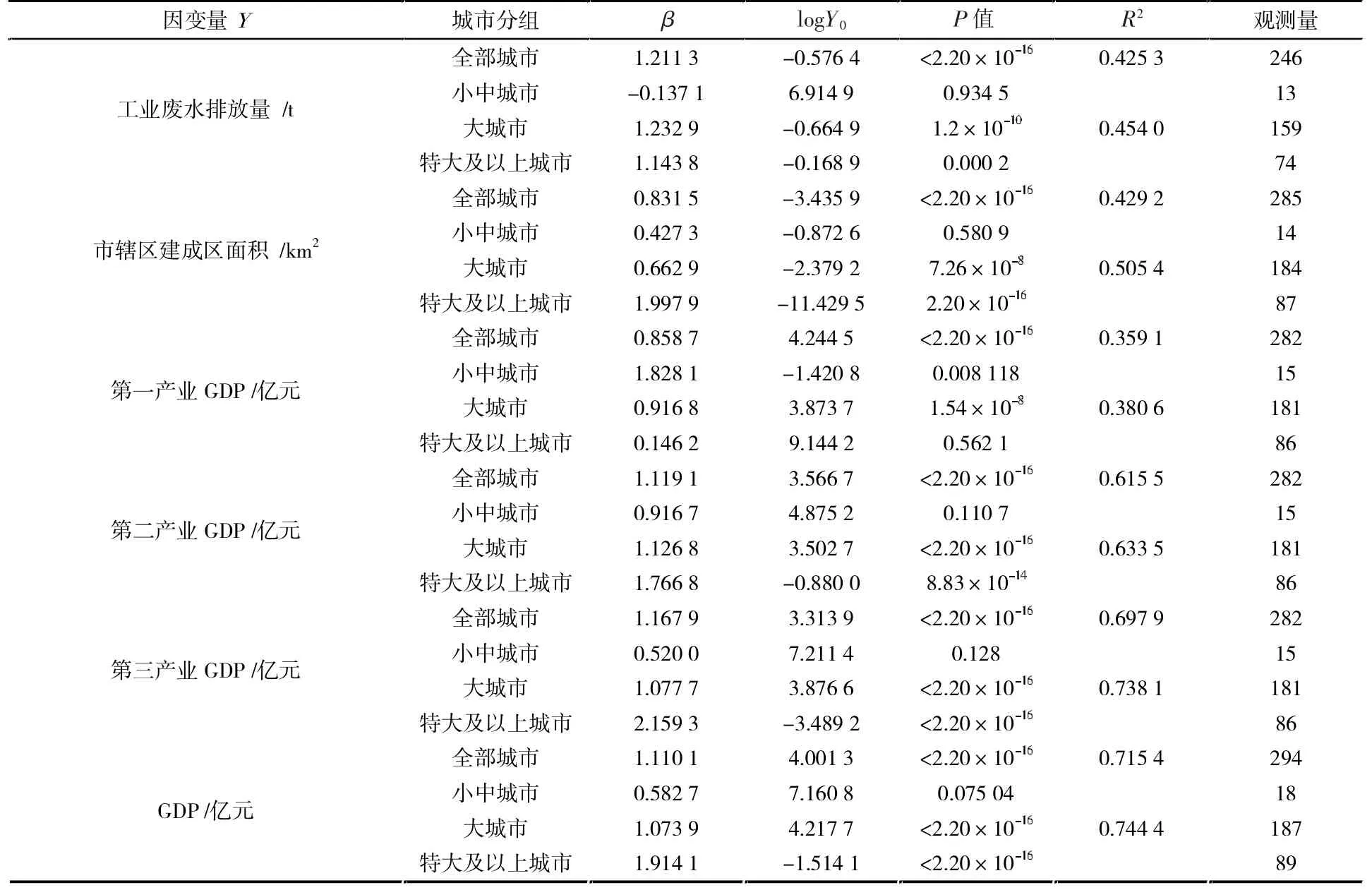
表1 不同規模城市下各指標擬合結果

3.4 不同城市指標下各個城市規模的分析

下面對不同城市指標的各個城市規模進行討論。以GDP 為例，小中城市β 估值均小于1，說明以上指標在該城市規模為次線性指標，體現了分散效應；大城市、特大及以上城市β 估值均大于1，說明該指標為超線性指標，體現了規模報酬遞增效應。對于截距logY0的估值，特大及以上城市logY0估值均為負值，說明該指標中0＜Y＜1，具有收縮作用；小中城市、大城市logY0估值均為正值，說明該指標中Y＞1，具有擴大作用。大城市、特大及以上城市的P 值小于0.001，該方程在P=0.001 水平上通過了顯著性檢驗。R2約等于0.74，擬合優度較好。對于其他五種城市指標的結果解讀同上。

4 結果與討論

4.1 結果

從擬合優度R2來看，折線圖的模型在對異質性數據進行處理時更精確，回歸效果更顯著，將城市按規模進行區分并分段回歸的效果要高于將所有城市視為總體進行線性回歸的結果。

在模型參數解讀方面，異速標度指數β 本質上是分維之比，是同一個系統的兩種測度相對增長率之比[19-21]。針對異速標度指數與1 的大小關系，可以將其分成正異速生長（β＞1）、同速生長（β=1）和負異速生長（β＜1）。就建成區面積—人口規模異速標度指數而言，該指數可作為城市化過程中城市土地利用合理程度的一個定量判別依據。當β＞1，城市常住人口擴張的速度小于城市建成區面積擴張的速度，城市用地浪費；當β＜1，城市人口擴張的速度大于城市建成區面積擴張的速度，城市用地節約；當β=1，城市人口擴張的速度等于城市建成區面積擴張的速度，城市用地恒定。針對擬合結果，發現特大及以上城市用地浪費，小、中城市及大城市用地節約。針對GDP—常住人口規模異速標度指數，當β＞1，城市人口增長率大于經濟增長率，存在經濟產出集聚效應；當β＜1，城市人口增長率小于經濟增長率，存在分散效應；當β=1，城市人口增長率等于經濟增長率，經濟發展穩定。針對擬合結果，發現大、特大及以上城市經濟發展存在集聚效應，小、中城市經濟發展存在分散效應。

4.2 討論

文中將2018 年中國294 個地級市的數據代入得出大、特大及以上城市經濟發展存在集聚效應，小、中城市經濟發展存在分散效應的結論，符合實際城市發展的經濟規律。通過文中的研究可以給予城市發展模式的思考，究竟選擇城市集聚發展還是城市分散發展的經濟模式，不僅取決于城市規模，還取決于城市人口的擴張速度。

在以往的城市標度律研究中，擬合的方式一般采用直線擬合，但這往往會忽視數據可能存在的異質性，從而導致擬合結果較差或參數不符合實際情況，而分段折線擬合更適用于處理存在異質性的數據，可以較好地處理了上述情況。在一定的誤差范圍內，利用分段折線擬合的方式，用折線來代替一整條直線，并將擬合的結果呈現在同一張圖中，這樣可以直觀地展現出不同城市規模下某種指標的擬合結果，方便進行對比。此外，折線擬合得到的擬合優度，相比較直線圖而言，折線圖的模型在對異質性數據進行處理時更精確，回歸效果更顯著，回歸擬合效果更好，提高了數據分析的嚴肅性、有效性和準確性。

然而文中的研究模型也有一定的局限性。第一，對于資源型城市，該模型并不適用，需要尋找更加合理的標度律去度量城市的發展水平；第二，城市標度律模型需要建立在“互動”的社會經濟活動基礎上，即需要人口流動、知識交流、經濟流通等條件；第三，城市標度律系數會隨著空間尺度的變化而變化，以市轄區為劃分尺度是最理想的，但事實上，我國部分城市依然存在這大量的非城市化地區，這對于城市標度律模型的應用是一種挑戰[13]。

研究不同城市規模下中國城市發展指標、中國城市發展的內在規律和影響因素對中國城市的可持續發展尤為重要。因此，以下問題將是未來的研究方向：（1）在基礎設施建設、文化發展、科技水平等方面，是否存在更好地衡量城市、區域發展狀況的城市指標；（2）對于其他的城市規模劃分（如長三角地區、珠三角地區、京津冀地區），城市標度律的適用性如何，哪些數據和空間尺度更能反映城市標度律；（3）在規模修正、減小誤差等方面，城市標度律模型是否可以繼續完善。

5 結語

由文中建模結果分析，結合我國實際情況，針對我國城市的發展提出如下建議：（1）對于特大及以上城市，適當降低建成區面積擴張的速度，實現有效且高效擴張，以避免出現城市用地浪費的現象。（2）對于小中城市，在繼續保持第一產業穩定發展的基礎上，進一步鼓勵第二產業和第三產業的發展，國家提供技術支持和資金保障，拉動小中城市穩健發展，從而提高城市經濟水平；相反，對于特大及以上城市，在發展第二產業和第三產業的同時，更要保障其第一產業的發展滿足第二產業和第三產業的需求，以實現各產業均衡發展，從而進一步提升特大及以上城市的經濟實力。（3）對于小中城市，要促進各產業的綜合發展，積極響應國家相關扶持政策，完善基礎設施建設，促進經濟高速發展，進而實現中國城市經濟的穩步發展。