基于自適應(yīng)動態(tài)規(guī)劃的移動機器人視覺伺服跟蹤控制

羅 彪 歐陽志華 易昕寧 劉德榮

隨著移動機器人控制技術(shù)的發(fā)展,移動機器人如今已廣泛應(yīng)用于工業(yè)生產(chǎn)、國防軍事以及生活服務(wù)等眾多方面[1].視覺傳感器近年來逐漸變得價格經(jīng)濟、易于獲取,加上其本身具有獲取環(huán)境信息豐富、外部感知能力強和適用范圍廣等特點,因而廣泛裝備于移動機器人和其他智能體系統(tǒng)[2].由于視覺傳感器的作用,移動機器人的靈活性和智能性得到極大提高,可以適應(yīng)更加復(fù)雜的環(huán)境,基于視覺的機器人的定位、環(huán)境感知與控制技術(shù)也得到了很大的發(fā)展[3].移動機器人視覺伺服控制主要有兩大控制目標(biāo),一種是位姿校正[4],另一種是軌跡跟蹤[5].在實際應(yīng)用中,軌跡跟蹤相比位姿校正往往更加復(fù)雜且常見,因此基于視覺的移動機器人軌跡跟蹤吸引了大量學(xué)者的關(guān)注與研究.

經(jīng)典的視覺伺服控制主要分為基于圖像的、基于位置的和混合視覺伺服控制.基于圖像的視覺伺服控制是通過在二維圖像平面定義誤差信號進行控制,不需要利用移動機器人三維位姿信息,且其對系統(tǒng)擾動具有魯棒性,但是很難控制移動機器人的偏轉(zhuǎn)位姿[6].基于位置的視覺伺服控制需要在三維歐氏空間定義誤差信號,雖然需要進行三維重構(gòu),但這樣直接對三維空間的誤差進行控制可以保證其收斂性.由于移動機器人具有非完整約束特點以及單目相機深度信息的缺失造成系統(tǒng)帶有不確定性參數(shù),設(shè)計移動機器人的控制器存在很多困難[7].根據(jù)Brockett 定理,連續(xù)定常的控制器無法實現(xiàn)對具有非完整約束的移動機器人位姿校正控制[8].為了克服非完整約束,文獻[9]提出了一種基于反步法的時變狀態(tài)反饋跟蹤控制方法.然而其并未將視覺傳感器引入到控制中,并且一般假設(shè)系統(tǒng)狀態(tài)是精確可測量的.但在移動機器人的視覺伺服跟蹤控制中,由于視覺傳感器的引入給系統(tǒng)帶來了不確定性,以往的設(shè)計方法并不能直接應(yīng)用于視覺伺服控制中.為了克服這些限制,目前已提出了許多非線性控制方法.文獻[5]基于單應(yīng)性技術(shù)設(shè)計了一種自適應(yīng)控制器實現(xiàn)移動機器人的軌跡跟蹤任務(wù),其視覺反饋由搭載于機器人上的相機提供.為保持目標(biāo)特征點在攝像機的視野范圍內(nèi),文獻[10]設(shè)計了一種時變連續(xù)的混合視覺伺服控制器實現(xiàn)對移動機器人一致性跟蹤與位姿校正任務(wù).為了在無需知道移動機器人位姿與速度信息下完成軌跡跟蹤任務(wù),文獻[11]提出了一種自適應(yīng)控制方法實時估計移動機器人的位姿與速度.近期,也有一系列關(guān)于移動機器人的視覺伺服跟蹤控制的相關(guān)成果[12-15].在上述針對移動機器人的視覺伺服跟蹤控制中,大多是為完成視覺跟蹤任務(wù),但考慮最優(yōu)性能指標(biāo)的移動機器人視覺伺服最優(yōu)跟蹤控制問題仍待研究.

考慮到移動機器人的視覺伺服軌跡跟蹤控制問題的系統(tǒng)模型是一個時變仿射非線性系統(tǒng).自適應(yīng)動態(tài)規(guī)劃(Adaptive dynamic programming,ADP)是解決非線性最優(yōu)控制問題的一種有效的方法[16-21].ADP 作為一類智能控制方法,可以有效地解決傳統(tǒng)動態(tài)規(guī)劃中“維數(shù)災(zāi)”的問題,同時具備處理復(fù)雜約束和不確定性的能力.這類方法在處理具有強非線性、強耦合性的復(fù)雜非線性系統(tǒng)時,具有自適應(yīng)性、最優(yōu)性和穩(wěn)定性[22].求解基于ADP 的移動機器人視覺伺服軌跡跟蹤的最優(yōu)控制,需要求解哈密頓-雅可比-貝爾曼(Hamilton-Jacobi-Bellman,HJB)方程.對于非線性定常系統(tǒng)來說,其HJB 方程是一個時不變的偏微分方程,無法求得其解析解,目前大部分求解方法都是設(shè)計合適的神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)來近似未知項[23-24].文獻[25]針對非線性不確定系統(tǒng)設(shè)計了三個神經(jīng)網(wǎng)絡(luò)分別近似系統(tǒng)狀態(tài)、值函數(shù)和最優(yōu)控制.在系統(tǒng)模型已知的情況下,文獻[26]針對移動機器人控制問題提出了一種單網(wǎng)絡(luò)自適應(yīng)評價方法.與上述一般非線性系統(tǒng)不同的是,由于移動機器人系統(tǒng)模型固有的時變特性,最優(yōu)控制問題中的HJB 方程含有兩項偏微分項,且值函數(shù)是狀態(tài)與時間的函數(shù),這使得問題更加復(fù)雜.在現(xiàn)有的研究中針對時變系統(tǒng)的最優(yōu)控制還較少.目前有兩種神經(jīng)網(wǎng)絡(luò)的結(jié)構(gòu)用于近似與時間相關(guān)的值函數(shù): 1)帶時變權(quán)值的神經(jīng)網(wǎng)絡(luò)[27-28];2)常數(shù)權(quán)值與時變激活函數(shù)的神經(jīng)網(wǎng)絡(luò)[29-30].

當(dāng)前基于ADP 的移動機器人視覺伺服控制方法及理論仍然是一個開放性問題,有待深入研究.本文的貢獻主要體現(xiàn)在以下幾個方面.

1)針對移動機器人視覺伺服控制,提出了基于ADP 的跟蹤控制方法.與現(xiàn)有視覺伺服控制方法相比,本文設(shè)計的ADP 控制方法是基于最優(yōu)控制理論,算法收斂后,可得到近似最優(yōu)控制器.

2)現(xiàn)有的大多數(shù)工作針對定常系統(tǒng)設(shè)計,而移動機器人視覺伺服控制系統(tǒng)為時變系統(tǒng),得到的HJB方程是時變的.因而,本文的工作與現(xiàn)有ADP 方法在理論分析與實現(xiàn)存在顯著區(qū)別,這是本文主要解決的理論難題.同時,本文所提的基于ADP 的跟蹤控制方法對于一般性的時變仿射非線性系統(tǒng)的跟蹤控制問題具有普適性和通用性.

3)針對時變HJB 方程,本文設(shè)計了帶時變權(quán)值的神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu),給出了一種新的權(quán)值更新律,證明了神經(jīng)網(wǎng)絡(luò)權(quán)值的收斂性和閉環(huán)系統(tǒng)的穩(wěn)定性.同時,在實驗仿真中驗證了該類結(jié)構(gòu)具有較小的誤差和快速收斂性.

針對時變非線性系統(tǒng)的最優(yōu)控制仍然與時不變系統(tǒng)存在不同之處,同時帶來許多挑戰(zhàn).本文針對移動機器人視覺跟蹤控制問題,提出了一種新穎的基于ADP 的跟蹤控制方法.考慮移動機器人系統(tǒng)模型的時變特性與非完整約束,采用帶時變權(quán)值的神經(jīng)網(wǎng)絡(luò)近似值函數(shù),并給出了一種新的權(quán)值更新律.運用Lyapunov 穩(wěn)定性理論證明了權(quán)值的收斂性以及閉環(huán)系統(tǒng)狀態(tài)是一致最終有界的.

1 問題描述

如圖1 所示,本文考慮帶有單目相機的輪式移動機器人,假設(shè)移動機器人的坐標(biāo)系與相機坐標(biāo)系相同.當(dāng)前相機坐標(biāo)系記為Fc,坐標(biāo)系Fc的原點為移動機器人中心,x軸方向為與移動機器人輪軸平行,z軸方向為相機光軸方向.由右手坐標(biāo)系規(guī)則,y軸垂直于移動機器人運動平面xz向下.坐標(biāo)系Fd與F*分別表示移動機器人在期望位姿和在固定參考位姿處的坐標(biāo)系,其x,y,z軸的定義規(guī)則與坐標(biāo)系Fc相同.在移動機器人的軌跡跟蹤任務(wù)中,期望軌跡在Fd中由一系列關(guān)于特征點的圖像描述.F*為固定參考坐標(biāo)系,由一張關(guān)于特征點的圖像表示.θd和θ分別表示Fd與Fc相對參考坐標(biāo)系F*繞y軸的旋轉(zhuǎn)角.基于以上的坐標(biāo)系定義,本文的目標(biāo)是設(shè)計一種視覺伺服跟蹤控制器以確保移動機器人完成軌跡跟蹤任務(wù),即當(dāng)t→∞時,Fc→Fd.

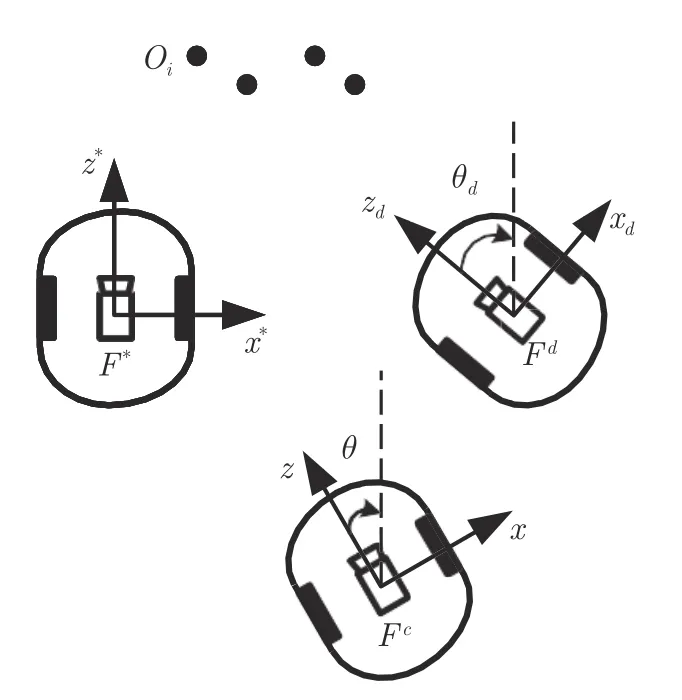
圖1 視覺伺服軌跡跟蹤任務(wù)描述Fig.1 Visual servoing trajectory tracking task

1.1 歐氏重構(gòu)

如圖1 所示,假設(shè)移動機器人僅做平面運動,坐標(biāo)系F*在坐標(biāo)系Fc中的位姿信息可以由[x,z,θ]T表示.其中,x和z分別表示沿著x軸和z軸方向的平移,θ表示繞y軸的旋轉(zhuǎn).同樣,坐標(biāo)系F*在坐標(biāo)系Fd中的位姿信息可以由[xd,zd,θd]T表示.考慮N個共面的靜止特征點Oi(i=1,2,···,N),其在坐標(biāo)系Fc,Fd,F*的三維坐標(biāo)分別為定義為

由針孔相機模型可以得到特征點歸一化三維歐氏坐標(biāo)與可測量齊次像素坐標(biāo)的關(guān)系為

其中,Hc,Hd ∈R3×3分別為當(dāng)前位置、期望位置與參考位置之間的單應(yīng)性矩陣.通過直接線性變換算法,可以將單應(yīng)性矩陣Hc分解得到當(dāng)前相機的尺度化平移和旋轉(zhuǎn)角θ;同樣地,將單應(yīng)性矩陣Hd分解得到期望的尺度化平移和旋轉(zhuǎn)角θd[31].具體定義為

其中,d*為深度信息常量,表示固定參考坐標(biāo)系F*的原點到特征點平面的距離,即d*=由前文的描述可知,當(dāng)t→∞時,若則表示移動機器人完成了軌跡跟蹤任務(wù).

1.2 移動機器人運動學(xué)模型

移動機器人Fc的位姿信息在坐標(biāo)系F*中記為[x*,z*,θ*].經(jīng)典的移動機器人連續(xù)時間運動學(xué)模型可以表達(dá)為

其中,v和ω分別為移動機器人的線速度與角速度.通過坐標(biāo)變換可以得到 [x,z,θ]T與[x*,z*,θ*]T之間的關(guān)系,即

對式 (9)求關(guān)于時間t的導(dǎo)數(shù),并將式 (8)代入求導(dǎo)結(jié)果,可得

將式 (7)代入式 (10)和式 (11),可得

1.3 跟蹤誤差系統(tǒng)模型

移動機器人軌跡跟蹤誤差定義為

其中,ex,ez表示平移誤差,eθ為旋轉(zhuǎn)誤差.由式 (14)可知,當(dāng)e→0 時,則因此上述問題轉(zhuǎn)換為設(shè)計一反饋控制律使得e→0,則表示移動機器人完成了軌跡跟蹤任務(wù).對式 (14)求關(guān)于時間的導(dǎo)數(shù),并將式 (12)和式 (13)代入,可得

為了便于后續(xù)對跟蹤控制問題控制器的設(shè)計,受文獻[32]啟發(fā),使用如下輸入變換:

其中,uv,uω為新的輸入控制量,可見上述變換也是可逆的.由此可以推導(dǎo)出新的誤差模型,即

為估計深度參數(shù)信息,深度參數(shù)d*的估計更新律設(shè)計采用與文獻[33]類似方法,且其收斂性已在文獻中得到證明.

2 控制器設(shè)計

在移動機器人跟蹤控制任務(wù)中,期望軌跡的速度vd(t),ωd(t)是隨時間變化的,導(dǎo)致在誤差模型 (17)中含有時變項.本節(jié)基于ADP 方法設(shè)計最優(yōu)控制器以保證移動機器人完成軌跡跟蹤任務(wù),采用評價神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)近似最優(yōu)值函數(shù),求解最優(yōu)控制輸入.

2.1 最優(yōu)控制設(shè)計

由誤差動力學(xué)方程 (17)可知,該系統(tǒng)是一個連續(xù)時間仿射非線性系統(tǒng),可以表示為

其中,

注意到系統(tǒng)狀態(tài)方程 (18)中控制輸入為二維,而系統(tǒng)狀態(tài)為三維,可見該系統(tǒng)是一個欠驅(qū)動系統(tǒng).

針對此系統(tǒng)的最優(yōu)控制問題,本文的目標(biāo)是設(shè)計一個反饋控制策略使得下列定義的值函數(shù)最小,即

其中,效用函數(shù)取為L(e,u,t)=Q(e)+uTRu,Q(e)是正定的,即對于?e0,Q(e)＞0 且e=0?Q(e)=0,R∈R2×2為對稱正定矩陣.沿著系統(tǒng)軌跡(18),對值函數(shù)求時間微分,可得如下時變Lyapunov方程[34]

注意到與其他仿射非線性系統(tǒng)無窮時域最優(yōu)控制情況不同,式 (21)是與時間t直接相關(guān)的.根據(jù)最優(yōu)性原理,當(dāng)=0 時,可得最優(yōu)控制為

將式 (22)代入式 (20),可得時變HJB 方程

注意到HJB 方程 (23)是一個偏微分方程,很難直接求得此方程的解析解,因此這里使用神經(jīng)網(wǎng)絡(luò)近似估計最優(yōu)值函數(shù)V*(e,t),以期望求得近似最優(yōu)的反饋控制.

2.2 神經(jīng)網(wǎng)絡(luò)近似

與時不變仿射非線性系統(tǒng)最優(yōu)控制問題不同的是,這里的最優(yōu)值函數(shù)V*(e,t)與時間變量t相關(guān).受文獻[35]啟發(fā),帶時變權(quán)值的神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)可以用來近似一致連續(xù)時變函數(shù).假設(shè)V*(e,t)是光滑的,則最優(yōu)值函數(shù)V*(e,t)可由下列神經(jīng)網(wǎng)絡(luò)形式表示

其中,W(t)∈RL為真實的神經(jīng)網(wǎng)絡(luò)權(quán)值向量,L ∈R,L＞0為隱含層節(jié)點數(shù),隨著神經(jīng)網(wǎng)絡(luò)隱含層節(jié)點數(shù)增加,逼近誤差會不斷減小[35],即當(dāng)L→∞,ε(e,t)→0.?(e)=[?1(e),···,?L(e)]T∈RL為與狀態(tài)相關(guān)的連續(xù)可微的激活函數(shù),ε(e,t)為神經(jīng)網(wǎng)絡(luò)逼近誤差.對最優(yōu)值函數(shù)V*(e,t)求分別關(guān)于e和t的偏導(dǎo)

假設(shè) 2.神經(jīng)網(wǎng)絡(luò)逼近誤差ε(e,t)以及其分別關(guān)于狀態(tài)e與時間t的偏導(dǎo)數(shù)?eε(e,t),?tε(e,t)是有界的.真實的神經(jīng)網(wǎng)絡(luò)權(quán)值W(t)以及其對時間的導(dǎo)數(shù)是有界的,激活函數(shù)?(e)以及其對e的偏導(dǎo)數(shù)?e?(e)是有界的: ‖ε(e,t)‖≤εM,‖?eε(e,t)‖≤εeM,‖?tε(e,t)‖≤εtM,‖W(t)‖≤WM,≤WtM,‖?(e)‖≤?M,‖?e?(e)‖≤?eM.

將式 (25)代入式 (22)中,最優(yōu)控制輸入可以表示為

其中,D1(e)=g(e)R-1gT(e).根據(jù)文獻[36],隨著神經(jīng)網(wǎng)絡(luò)隱含層節(jié)點數(shù)L→∞,HJB 方程殘差εhjb(e,t)→0,即對于?εh＞0,?L:‖εhjb(e,t)‖＜εh.

2.3 神經(jīng)網(wǎng)絡(luò)權(quán)值更新

由于真實的神經(jīng)網(wǎng)絡(luò)權(quán)值W是未知的,設(shè)計一個評價神經(jīng)網(wǎng)絡(luò)近似最優(yōu)值函數(shù) (24),即

定義真實最優(yōu)控制輸入與近似最優(yōu)控制輸入之差為

將式 (27)和式 (31)代入式 (32)中,可得

將式 (30)和式 (31)分別作為近似最優(yōu)值函數(shù)和近似最優(yōu)控制代入哈密頓函數(shù) (21)中,可得

根據(jù)式 (34),定義目標(biāo)誤差函數(shù)為

為使目標(biāo)誤差函數(shù)E不斷減小,結(jié)合梯度下降法的思想設(shè)計權(quán)值更新律為

根據(jù)式 (36),可得

將等式 (38)左邊第2 項移到右邊,可得

由式 (39),可得:

根據(jù)式 (31),可得

3 穩(wěn)定性分析

定理 1.針對式 (18)描述的非線性時變仿射系統(tǒng),以式 (31)為控制輸入,式 (36)為評價神經(jīng)網(wǎng)絡(luò)的權(quán)值更新律,則閉環(huán)系統(tǒng)的狀態(tài)e與評價網(wǎng)絡(luò)的權(quán)值估計誤差是一致最終有界的.

證明.選擇Lyapunov 函數(shù)形式為

將式 (18)、式 (25)和式 (26)代入式 (48),可得

將式 (31)代入式 (49),可得

根據(jù)HJB 方程 (28),可得

將式 (52)代入式 (51)中,可得

將式 (47)和式 (53)相加,可得Lyapunov 函數(shù)的導(dǎo)數(shù)為

根據(jù)假設(shè)1 和假設(shè)2,可得

因為Q(e)是正定的,存在一個λq使得eTλqe≤Q(e).根據(jù)文獻[36],隨著神經(jīng)網(wǎng)絡(luò)隱含層節(jié)點數(shù)L的增大,HJB 方程殘差εhjb(e,t)會逐漸收斂到零.假設(shè)存在一正數(shù)εhM,選擇合適的神經(jīng)網(wǎng)絡(luò)隱含層節(jié)點數(shù)L,HJB 方程殘差滿足:εhjb≤εhM.因而,根據(jù)式 (54)和式 (55),可得

其中,

式中,I為合適維度的單位矩陣.選擇參數(shù)使H1＞0,根據(jù)式 (56),如果

在這里,有必要討論一下本文與相關(guān)工作[16,37-39]的區(qū)別.在文獻[37-38] 中,采用基于策略迭代方法設(shè)計控制器,與此不同,本文則是基于ADP設(shè)計自適應(yīng)控制器,因而在實現(xiàn)方法與理論分析上存在著顯著的差異.在文獻[16,39]中,考慮的是非線性離散時間系統(tǒng)的跟蹤控制問題,與本文方法的區(qū)別主要體現(xiàn)在: 文獻[16,39]考慮的是定常系統(tǒng),也就是說,雖然期望軌跡為時變的,但是針對的系統(tǒng)是定常系統(tǒng),也即時不變系統(tǒng);與文獻[16,39]不同,本文考慮移動機器人視覺伺服跟蹤控制問題,不僅期望軌跡是時變的,而且系統(tǒng)也是時變的.因此,文獻[16,39]與本文所針對的問題是完全不同的.

4 仿真研究

為了驗證本文提出的控制方法的有效性,本節(jié)利用計算機進行仿真實驗.選擇4 個共面特征點作為視覺目標(biāo)點,以便能通過單應(yīng)性矩陣分解成對應(yīng)的平移與旋轉(zhuǎn)量.相機標(biāo)定矩陣為

圖2～9 展示了實驗仿真結(jié)果.由圖2 和圖3可以看出,在本文設(shè)計的控制方法下系統(tǒng)狀態(tài)最終收斂到零并且控制輸入也隨著時間最終趨于零.神經(jīng)網(wǎng)絡(luò)的權(quán)值最終如期望的一樣收斂于常數(shù)值如圖4 所示,最終收斂權(quán)值為=[0.0445,0.0458,0.0214,0.0048,0.0180,-0.0005,0.0652,0.0174,0.0004,0.0430,0.0292,0.0021,-0.0021,-0.0011,-0.0009,0.0077,0.0105,0.0048,0.0003,0.0012,-0.0001]T.移動機器人的線速度和角速度如圖5 所示,可以看出,當(dāng)前線速度和角速度與期望軌跡的線速度和角速度逐漸一致.

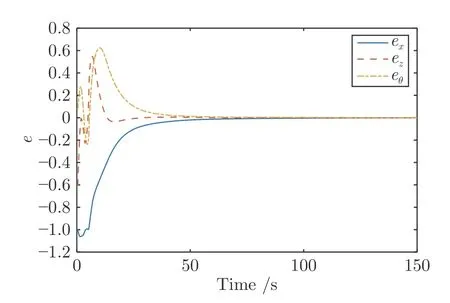
圖2 系統(tǒng)響應(yīng)Fig.2 System response

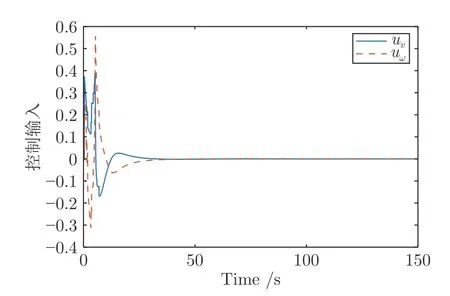
圖3 控制輸入Fig.3 Control input

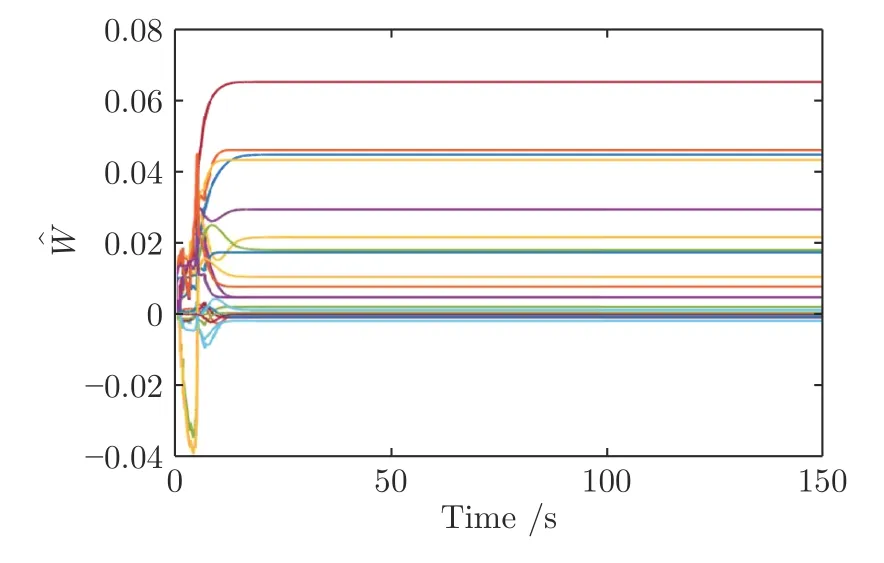
圖4 評價神經(jīng)網(wǎng)絡(luò)權(quán)值的收斂Fig.4 Convergence of critic neural network weights

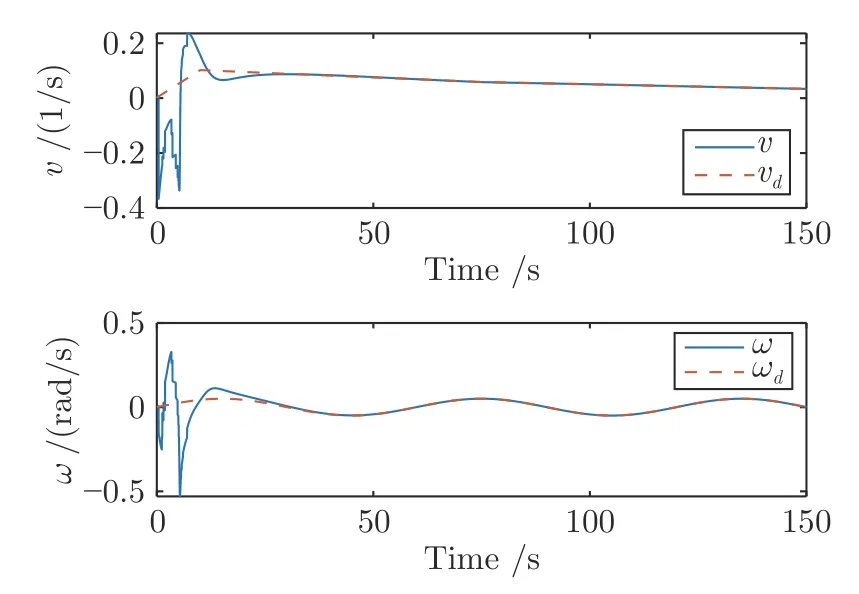
圖5 移動機器人期望軌跡速度與實際運動速度Fig.5 Desired and real velocities of the mobile robot

在仿真過程中,為了驗證本文所提出算法的效果,在保證選取同樣網(wǎng)絡(luò)層數(shù)和隱含層節(jié)點個數(shù)的前提下,將本文提出的時變權(quán)值神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)與文獻 [38] 中提出的時變激活函數(shù)NN 結(jié)構(gòu)進行對比.在最優(yōu)控制問題中,HJB 方程的近似誤差可以用于表征控制器對性能指標(biāo)優(yōu)化程度的好壞.如圖6 所示,在兩種方法下HJB 方程的殘差最終均能收斂至零,但本文所提方法的收斂速度相對要快很多.

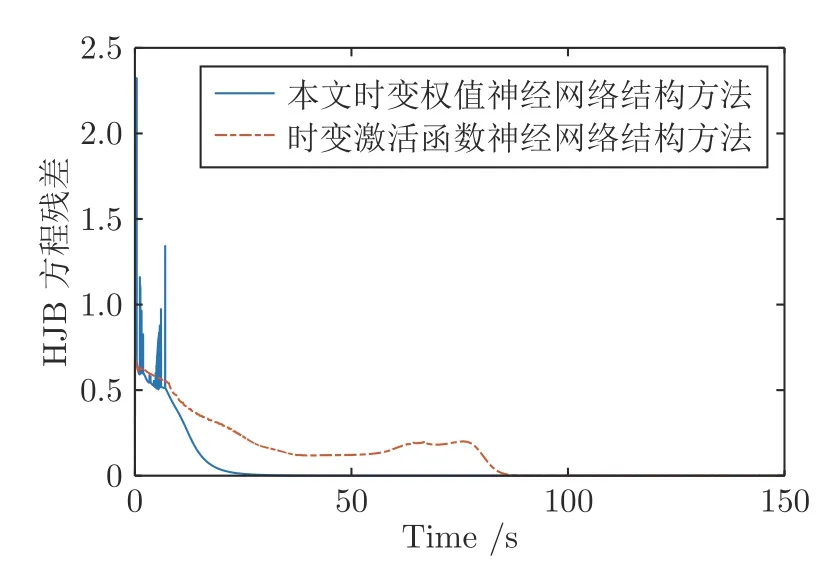
圖6 HJB 方程殘差Fig.6 The residual error of HJB equation

在兩種方法下的移動機器人期望軌跡與實際運動軌跡如圖7 和圖8 所示.可見,在本文所提的時變權(quán)值的神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)方法下,機器人的跟蹤效果更好、跟蹤誤差更小.此外,特征點的二維圖像軌跡如圖9 所示.其中,紅色虛線表示期望圖像軌跡,實心圓點表示初始的期望圖像,五角星表示最終的期望圖像;藍(lán)色實線表示當(dāng)前的真實圖像軌跡,空心圓點表示初始的真實圖像,方形表示最終的真實圖像.由圖9 可知,當(dāng)前實際圖像軌跡與期望的圖像軌跡逐漸一致.

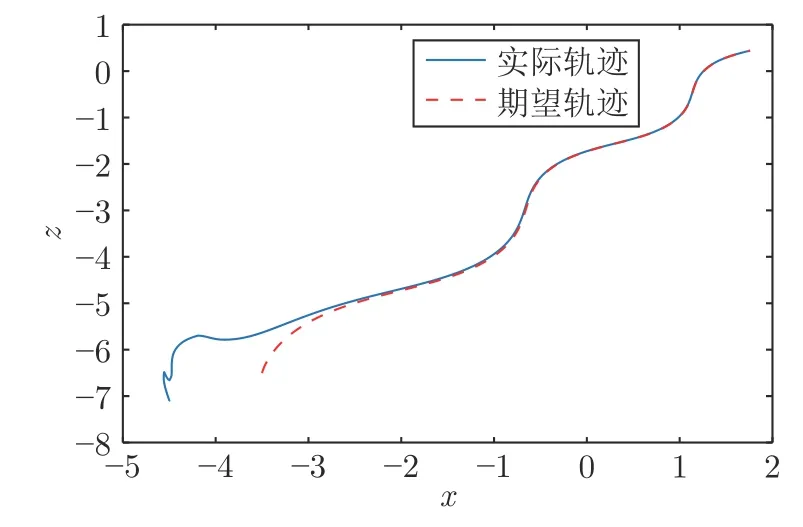
圖7 利用本文時變權(quán)值神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)方法的移動機器人期望軌跡與實際運動軌跡Fig.7 Desired and real trajectories of the mobile robot using time-varying weights neural network structure method in this paper

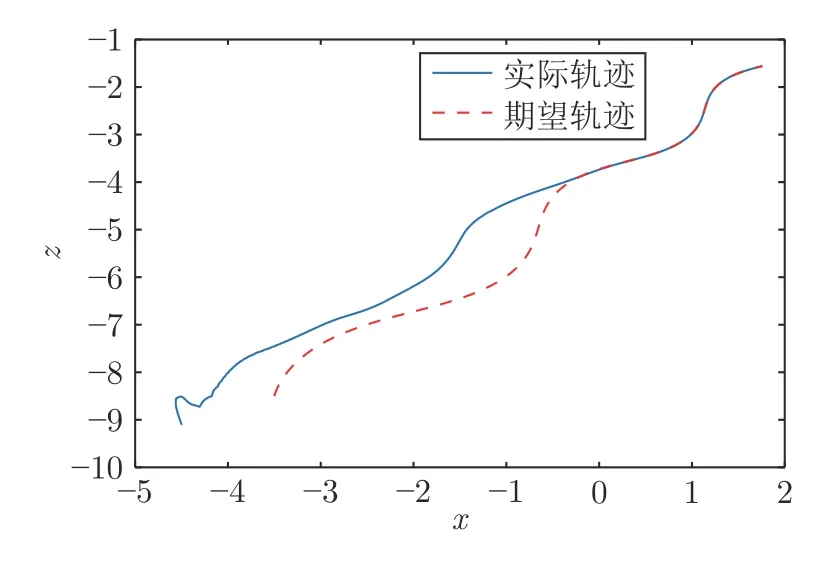
圖8 利用時變激活函數(shù)神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)方法的移動機器人期望軌跡與實際運動軌跡Fig.8 Desired and real trajectories of the mobile robot using time-varying activation neural network structure method

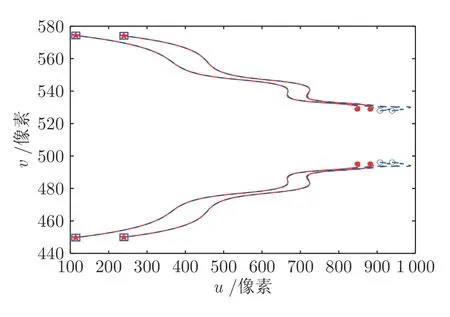
圖9 特征點二維圖像軌跡Fig.9 2D image trajectories of the feature points

5 結(jié)束語

本文設(shè)計了一種新的基于ADP 的跟蹤控制方法來解決移動機器人視覺伺服軌跡跟蹤最優(yōu)控制問題.與以往控制對象不同的是移動機器人視覺伺服軌跡跟蹤的誤差系統(tǒng)模型是一個時變仿射非線性系統(tǒng),針對此系統(tǒng)的最優(yōu)控制問題需要設(shè)計具有時變權(quán)值的神經(jīng)網(wǎng)絡(luò)近似值函數(shù)以求解時變的HJB 方程.運用Lyapunov 穩(wěn)定性理論證明了在本文提出的控制方法作用下神經(jīng)網(wǎng)絡(luò)權(quán)值的收斂性以及閉環(huán)系統(tǒng)的穩(wěn)定性.仿真實驗結(jié)果驗證了所提出方法的有效性與可行性.