層層鋪墊，以“舊”換“新”

杜艷梅 蔣明

眾所周知，乘法分配律在整個數學學習中有著舉足輕重的地位和作用。根據課程標準的要求，現行小學數學教材主要采取了分散滲透與集中安排相結合的方式編排，大體分為三個階段：早期孕伏、逐步過渡、正式學習。下面，筆者就從這三個階段來談談自己在進行乘法分配律的教學中，對教材編排的一些理解和處理方法。

一、早期孕伏

（一）有關乘法分配律最初的知識儲備在教材中體現在二年級上冊第四單元《表內乘法一》，學生第一次真正接觸并初步認識乘法，明白乘法是求幾個相同加數的和的簡便運算，初步理解幾個幾的真正意義。具體操作如下。

1.（書）P48。（1）用3組小熊氣球，每組5個的方式呈現，學生實現從加法等式到乘法等式的自然過渡。學生初步理解加法和乘法之間的區別和聯系。（2）在“做一做”第1小題中，通過擺一擺，讓“幾個幾”的理解從抽象回歸具體。教學中，我在此練習基礎上增加了一組對比練習，在擺的過程中理解4個2和2個4的區別和聯系。（3）第2小題，用8串鑰匙圖再次強化對乘法意義的理解。（4）第3小題，在前面利用數形結合練習的基礎上，直接抽象、提升。（5）此外，根據學生的掌握情況，我設計了一道課后拓展題：利用所學知識，計算18×4的結果，以此強化加法和乘法之間的聯系和應用。在反饋的作業中，除了用加法的方式求得結果外，居然有學生通過擺小棒的，將算式寫成了18×4=10×4+8×4。

2.在乘加、乘減的新課教學之后，練習十二的第一題（見下圖），初看是一道簡單的鞏固練習題，細看，卻是編者再一次滲透乘法分配律知識的練習題。我在教學中等學生計算完，引導他們對比觀察，既能強化乘法意義（幾個幾），又對四年級下冊解決形如：101×78-78和99×78+78的簡便運算進行了初步教學。

（二）二年級上冊第六單元《表內乘法二》，重點教學7、8、9的乘法口訣，在有關乘法分配律知識的鋪墊和滲透上，除了和前面有相同之處，還有一定的提升，具體如下。

1.（書）P74。從乘加、乘減算式過渡到乘法算式，再到現在的以一道乘法算式為例，對應兩道乘加（減）算式。在處理這道練習題，我給了學生充足的時間去發現，然后匯報、交流。如：6個7等于5個7加1個7，也等于7個7減1個7。此時，我再追問：除此以外，6×7還可以用（ ）個7加（ ）個7或（ ）個7減（ ）個7，寫成算式形式：6×7=（ ）×7+（ ）×7或6×7=（ ）×7-（ ）×7，再次建立乘法分配律的初步模型。

2.在接下來的8和9的乘法口訣新課后的練習中再次鞏固練習，加深印象。

3.為了更好地理解掌握這部分知識，在單元結束后，我讓學生嘗試創編這樣的算式，2人一組，互測互評。

二、逐步過渡

計算學習是小學數學學習中的重頭戲，對于三年級上冊的多位數乘一位數的教學，我為乘法分配律的教學作了更進一步的知識儲備，具體體現在以下幾個方面。

（一）多位數乘一位數——口算。

1. 先談教材：教材第57頁（如下圖）。先從口算20×3入手，利用小棒幫助計算，然后過渡到12×3，小棒的擺放從最初的一行調整為豎著擺放，同時在小棒的下面配以相應的乘法算式，數形結合。

2.再談教法：教學中，我重點講解了12×3的橫式計算過程，利用小棒講“先分后合”，幫助學生理解算理——12×3=（10+2）×3=10×3+2×3=36。在接下來的作業處理中，我重點讓學生用“先分后合”的方法計算21×4、23×2、32×3，并說一說解題思路，理解其本質就是乘法意義的應用。最后，課后拓展，再次運用“先分后合”嘗試計算124×3.

（二）多位數乘一位數——筆算。1.（書）P60。教學筆算12×3時，我直接從前面所學的先分后合知識引入，把橫式寫成對應的豎式形式，順利完成不進位乘法的筆算教學。在這里，教師一定要明確12×3的豎式和12×3=10×3+2×3都是依據乘法分配律分別計算2個3加10個3，區別只是筆算寫成豎式，先分后合（即以后的簡便運算）寫成橫式而已。

2.（書）P62。在之后的進位乘法的教學中，我仍然采用將新知轉化為舊知的方法進行。筆算前讓學生先用先分后合的方法進行口算，會有24×9=24×10-24×1或24×9=20×9+4×9兩種不同形式，教師要加以適當的引導。

3.在本單元的整理和復習時，我給學生留了一道課后拓展題：24×26，以此培養學生的知識遷移及靈活運用知識的能力。

4.此外，在第8單元“分數的初步認識”第96頁例題教學中，同分母的加減法計算，也有意滲透了乘法分配律在分數中的應用。

三、正式學習

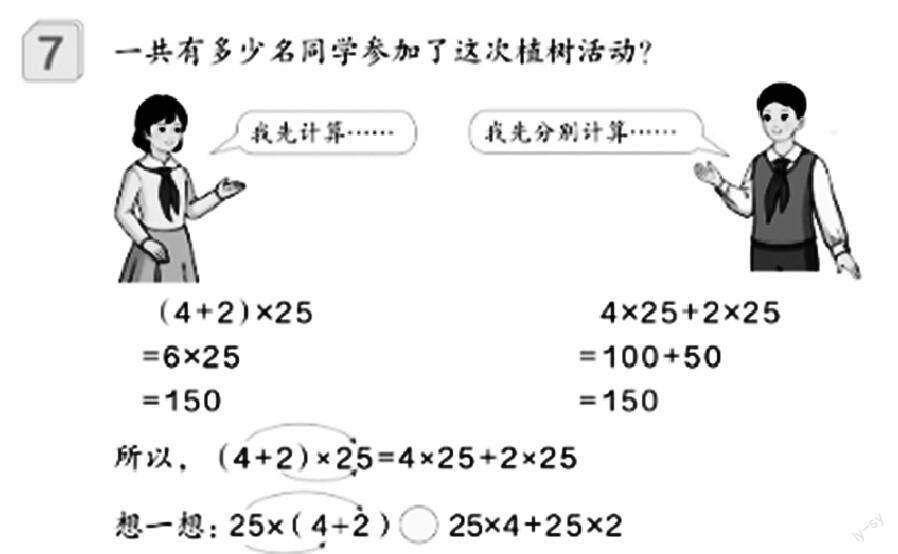
四年級下冊第3單元《運算定律》第26頁中，以一題多解的方式出現兩種不同的解題思路，根據算式和計算結果，可得出（4+2）×25=4×25+2×25。當這個新知識已然變成學生所熟悉的舊知時，學生的知識接受度更高。在這時，我便將這種形式模型化。從數字表示數到用字母代表數，把算術和代數有機地聯結起來，順利實現算術思維向代數思維的一次跨越，讓學生對乘法分配律的理解再次明晰且深刻。

當學生經歷了這樣知識積淀、遷移、運用的過程后，某個知識點掌握很棒是一方面，更重要的是數學素養的逐步形成才是最大的收獲。