素養為本的小學數學多維變式教學

金怡婷

[摘 要] 變式教學策略長期以來在數學教學中得到廣泛應用。但由于實施變式教學的主體——教師對該策略存在一定的認知偏差，加之教師群體實際教學水平參差不齊，當前變式教學出現了過于堆砌、流于形式、短于聯系等問題。因此，文章以核心素養為導向，嘗試用“三維共進”的方式，從“時間”“空間”和“時空”維度，創新傳統變式教學，解決當前變式教學存在的問題，力求將碎片化的學習變得完整、結構化，將機械低效的學習變得有趣、有效，將淺層的學習變得深入、高階，以多維變式引領學生學習，從而發展學生的核心素養。

[關鍵詞] 變式教學；深度學習；結構化學習；小學數學

變式是通過變換同類事物的非本質特征的表現形式，從而突出事物的本質特征。變式教學策略一直以來在數學教學中起著重要的作用。在變式教學中，教師通過合理變換概念或問題的非本質特征，使學生掌握數學對象的本質屬性，促進學生對學科內涵的深入理解。但由于部分教師對變式教學存在認知上的偏差，加上教師群體教學水平參差不齊，當前變式教學在實施中涌現出越來越多的問題。

新課標指出，要在實現知識進階的同時，體現核心素養的進階。多維變式教學嘗試更新觀念，解決傳統變式教學中存在的問題，以結構化視角統整數學知識體系，以多元組織形式推進數學課堂教學，以數學思想方法引領學生數學學習，依托具體的教學內容，逐漸培養學生的核心素養。

一、當前變式教學中存在的問題

（一）過于堆砌

在數學的習題講評課與復習課中，教師過分追求課堂容量，追求“多練”，設計了多而不精的變式練習，想以此來幫助學生加深概念理解，鞏固方法運用。但現實卻是學生常常陷入機械、重復、枯燥解答的困境，在這一過程中，師生都高度關注答題的數量與正確率，忽視了通過解決問題而可能取得的學生能力提升、經驗積累、思想發展等重要收獲，對學生核心素養發展的關注尤為缺失。這些低質堆砌的變式練習，由于缺乏應有的意義、趣味與挑戰，學生被動地參與學習，量大而效低。

（二）流于形式

通過變式，教師可以把問題拓寬，使知識向深處延伸，促進學生的思維向縱深發展。但如若教師只關注“變”，而忽視知識內容本質，將致使問題變得“刁鉆”且毫無意義，不僅使學生失去深入探究的興趣，也不利于學生對知識本質的理解，阻礙了學生發散性思維的生長。這樣，表面上為提質增效而設計的變式練習，實則流于形式，忽視了問題本質與核心內容，對學生發展毫無益處可言。

（三）短于聯系

傳統的變式教學中變式的維度比較單一，集中在相似題目或表征形式的變化上，較少關注變式的組織形式、教學方法、學生思維方式等的變化，也較少引導學生自主地進行變式探索。學生總是被動地接受教師的“指令”，很少真正自發地關聯個體認知基礎與認知結構特點，比如先前的經驗、當前收獲的經驗、未來經驗的預判、學習的情意等，不能用聯系的眼光看待學習內容，本該動態的學習過程變得靜止而呆板，無法走向深度學習。

二、多維變式教學的內涵

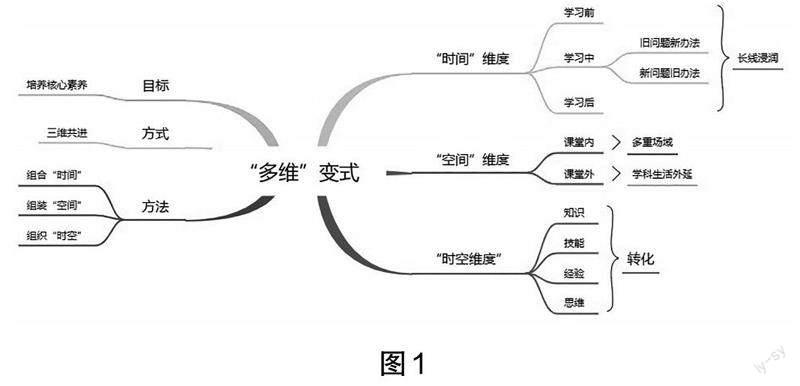
多維變式的“維”包括學生學習的時間維度（學習前、學習中、學習后）、空間維度（課堂內、課堂外）以及時空維度（知識與技能、經驗與思維間的轉化）。多維變式教學是“學生本位”的教學，是以發展學生核心素養為目標，以組合“時間”、組裝“空間”、組織“時空”的具體方法為抓手，以三維共進的方式展開教學。

多維變式立足于傳統變式，多維變式教學除了傳統變式教學中對問題形式、情境內容等的變換，更加注重方法、策略和思維方式的變更，以及教學組織形式、教學方法、教學模式等的變化。多維變式教學更多地關注知識的立體結構，關注學生在經驗與思維方面的收獲。多維變式教學嘗試將變式教學的元素延伸到課堂以外，重視學生學習過程“時間”維度的變化，使碎片化的學習變得完整、結構化；重視學生學習場域“空間”維度的變化，使機械低效的學習變得有趣、有效；重視學生素養發展“時空”維度的變化，使淺層的學習變得深入、高階。

多維變式教學試圖解決當前變式教學中的突出問題，有“破舊立新”之義，試圖從“時間”“空間”“時空”維度共進，創設合適的變式，讓知識在學生的認知結構上自主生成與建構，使不同層次的學生都學有所得。

三、多維變式的教學實踐

（一）“時間”維度變式，在長線中浸潤

學生知識與技能的獲得并不是一蹴而就的，而是在理解一個又一個相關聯的知識點，完成一個又一個相關聯的任務中逐步實現的。在這一過程中，學生不僅逐漸積累了多樣的解題方法與策略，還逐步形成了數學的思維方式。因此，在教學中，教師應當有意識地將同類問題進行整合，打破新舊問題間的壁壘，貫通知識間的聯系，將不同時間段的學習內容進行重疊與組合，在問題的變化中實現認知結構化。

1.舊問題新方法，貫通學習全程。多維變式教學不僅關注問題形式的變化，更關注解題方法的變化。比如，在教學五年級列方程解決實際問題時，經常發現學生更傾向于用原先的算術方法來解決問題，哪怕他們都認同列方程能更清晰地看出數量之間的關系。究其原因，這些問題并不是“新”問題，這些問題其實在之前的學習中就遇到過，其中的數據、情境等外在形式可能有一些變化，但實質并沒有變化。因此，教師不用刻意回避先前的“舊”問題，索性將問題放在一起進行比較，引導學生觀察解題方法的變化，關聯“新”“舊”方法，實現方法優化，也就能更好地建構認知。

這里需要說明的是，多維變式教學倡導方法的多元化，尊重每個學生的個性，在方法的關聯中強化概念理解，在方法的優化中完善認知結構。

2.新問題舊方法，打破知識壁壘。數學課程受課時分配的影響，知識大多以“點”的形式分散于教材中，如果不注意建立知識間的聯系，就容易造成學生的學習碎片化。基于此，多維變式關注了知識的“來龍”與“去脈”，不僅注意“朝前看”，還留心“回頭看”。

比如，在教學四年級“運算律”時，教師在學生完整經歷猜想—驗證—表征—結論這樣的認識過程后，讓學生帶著學習經驗探究乘法中是否也有這樣的運算規律，將原本兩課時的部分內容進行重疊，讓后續的知識學習成為先前學習的拓展與延伸，新的知識生長于舊的經驗之上。

（二）“空間”維度變式，在多重場域中生趣

在“多維”變式教學中，教師不止關注學生在課堂上的學習，還重視學生在課堂之外的學習（如課前學習、課后學習）。不管何種場域的學習，只要有有意義的教學素材，都應當想辦法建立其聯系，使其盡可能發揮出教學價值。因此，教師要善于發現學生在不同學習場域中所接觸到的相關知識元素，整體架構知識系統，讓結構化的知識促成學生結構化的思維。

1.變教學方法，萬物皆數學。古希臘數學家畢達哥拉斯認為“萬物皆數學”， 認為數學是構成宇宙的基礎。的確，人們生活的很多領域，諸如購物、運動、導航、作曲、建筑、探索太空……都與數學有關，甚至花草樹木、風雪雨露等自然現象也都隱藏著數學的奧秘。因此，數學的學習并不僅僅存在于數學課堂上，還有一部分來自課堂之外的廣闊空間。

正是考慮到這一點，多維變式教學也提倡“導學案”的應用，以此拓寬學生的學習空間。在“導學案”的引領下，學生根據給定的材料自主獲取信息、提煉要點、生發疑問、提出猜想、推理論證。到了課堂上，學生在教師的引導下對先前的學習展開質疑、反思、補充、歸納等思維過程。這樣“先學后教”的學習，為學生的個性化發展提供了更多的可能。“導學案”關注的是課前學習，在課后學習中，有一種學習工具比較具有代表性，即思維導圖。學生可以用繪圖的方式梳理新知識，與此同時，這些導圖也可以成為進一步學習的素材。在變化的學習場域中，課外空間與課堂空間發生交互，學生生活的現實世界與數學的抽象世界相聯系。

2.變組織形式，一切可思維。課堂上的數學學習空間也是多元的，不僅有我們所熟悉的師生場域，還有生生等更讓學生神往的學習空間。同樣的教學內容，不同的組織形式，將會帶來截然不同的教學效果。例如，在教學時，讓學生走上講臺來扮演教師的角色，講述自己或是所在小組的發現；又或者由個別學生與教師合作，共同解析重點與疑點知識。在學生自由而豐富的交流過程中，教師給予適時的引導，引發不同層次學生的思維碰撞，在不斷的質疑、補充或贊嘆中主動地思考，積極地建構。在多重場域的學習中，課堂組織形式的轉變，不僅激發了學生的學習興趣，同時帶來的還有素養的發展。

（三）“時空”維度變式，在轉化中發展

學習的發生是“隨時”“隨地”的，但高效的學習一定是符合“天時”“地利”的。多維變式將合適的時間與空間組織在一起，實現知識、技能、經驗、思維四者互相轉化。這需要教師關注學生的認知結構和知識的邏輯結構，動態把握學習的回應，關注學習的全過程。

1.觸發深度學習，使認知結構化。在復習課中，變式的使用最為常見。比如，在六年級“四則運算總復習”的教學中，很多教師會設計較多的運算變式練習，但在設計時，只在這些題目的數據上下功夫，通過大量的同類運算，以幫助學生加深體會。雖然這樣的變式能讓學生獲得一些計算經驗，但這樣的經驗是離散的。因此，除了讓學生經歷比較低水平的變式外，還應借助變式讓學生站在算理的角度去感悟算法的一致性。在實際教學中，教師可以嘗試讓學生總結各類數運算算理，還可以引導學生發現不同運算之間的聯系。在這樣的學習過程中，學生逐步將先前積累起來的散亂經驗重組，讓具有相同意義的經驗串聯，從而產生新知識，加固舊知識。

2.立足核心素養，完善思維結構。過去，教師一塊黑板、一支粉筆向學生講解最樸素的道理；現在，普及的電子產品、豐富的教學軟件、五彩繽紛的教學素材，讓大家可以不受時間與空間的限制，隨心學習，暢快學習。尤其是經歷了線上學習后，現代化的教學手段與教學方式越來越受到大眾的關注。日新月異的變化在訴說一個道理：學習如果局限于在校時間，拘泥于教室這個學習場所，那么學習是狹隘的。

在六年級下冊的綜合實踐課“大樹有多高”中，教師帶領學生走出教室，來到操場、廣場、公園，準備好竹竿、卷尺等工具，嘗試用比例的知識測量大樹的高度。變學習時間，變學習場域，課上與課后學習相結合，教室內與教室外學習相聯系，突破時間與空間限制。學生通過在變化的時間開展學習，收獲了“同一地點，不同時間，影長不同：早上與傍晚長一些，中午短一些”這樣的寶貴經驗；通過在變化的地點開展實驗，收獲了“同一時間，同一地點，影長與物體高度成正比”的學習體會。這些知識皆由不同維度的“變”而生。大樹到底有多高這個數學問題其實已經并不重要，重要的是學生將數學知識應用于真實的生活實踐，并將知識、能力、活動經驗與數學思考四者有機轉化與整合。與此同時，學生在合作交流中共同見證了數學的價值。

參考文獻

[1]中華人民共和國教育部.義務教育數學課程標準（2022年版）[S]. 北京：北京師范大學出版社， 2022.

[2]李昌官.走向素養為本的數學變式教學[J].課程·教材·教法，2021，41（8）：98-104.

[3]劉洋，楊超.“四基”視角下數學變式教學的“優”與“憂”[J].教育觀察，2020，9（15）：122-123.

[4]丁國蘭.注重變式教學，提升學生的思維能力[J].數學教學通訊，2019（26）：24-25，36.

[5]鄭福梅.利用變式教學培育數學學科核心素養的思考[J].數學教學通訊，2019（24）：36-37.

[6]朱俊華，吳玉國.結構化學習因“變式”而精彩[J].中小學教師培訓，2019（4）：63-65.

[7]鄭毓信.數學教育視角下的“核心素養”[J].數學教育學報，2016，25（3）：1-5.

[8]賴梅治.深度學習下小學數學教學探究與實踐[J].試題與研究，2021（24）：85-86.