多自由度混聯Ⅰ型慣容減震系統地震響應分析

李創第, 王瑞勃, 江麗富, 葛新廣

(1. 廣西科技大學 土木建筑工程學院,廣西 柳州 545006;2. 柳州工學院 土木建筑學院,廣西 柳州 545616)

近年來,消能減震技術在建筑結構的抗風抗震中得到廣泛應用[1-2],該技術通過在建筑結構的部分位置設置耗能裝置,使其在外部激勵作用下產生摩擦或剪切滯回變形等方式來消耗地震能量,從而達到降低結構動力反應的目的[3]。為此,眾多學者[4-6]對已有耗能裝置的改進及新型耗能裝置的開發進行了大量研究。20世紀末,“inerter”(慣容)[7]作為一種新型被動控制裝置被提出,慣容與傳統耗能裝置不同,它是兩端點的慣性元件,所產生的慣性力可表示為同質量量綱一致的慣容系數與兩端加速度的乘積。Ikago等[8]提出了以滾珠絲杠作為表觀質量放大器的調諧黏性質量阻尼器(tuned viscous mass damper,TVMD),并首次將TVMD應用于單自由度結構中,研究發現,TVMD相對黏滯質量阻尼器(viscous mass damper,VMD)、黏滯阻尼器(viscous damper,VD)的減震效果更為顯著。Wang等[9]研究了慣容在建筑懸架系統(即垂直基礎隔振)中的性能優勢,結果表明,慣容可以有效減小建筑系統的振動響應。在工程應用中,為進一步提高慣容的減震效果,常將慣容、彈簧以及耗能元件連接共同工作,三種元件連接所形成的動力系統稱之為慣容減震系統。根據三種元件的連接方式將慣容減震系統分為串聯型慣容系統、混聯Ⅰ型慣容系統和混聯Ⅱ型慣容系統[10-12]。串聯型慣容系統由慣容、彈簧、耗能元件三者串聯組成;混聯Ⅰ型慣容系統由彈簧、耗能元件并聯后再與慣容進行串聯形成;混聯Ⅱ型慣容系統由耗能元件、慣容并聯后再與彈簧串聯組成。Pan等[13]以結構隨機振動響應的減緩率為設計指標,提出三種慣容減震系統的單自由度結構基于白噪聲激勵的設計方法,該方法在給定響應減緩率的情形下可快速獲得單自由度慣容系統的關鍵參數,但所用白噪聲激勵與實際地震過程差異較大。Zhang等[14]發現并證明了阻尼增效現象的理論實質,基于阻尼增效方程提出了慣容減震系統通用的設計原理,運用實例對所提的方法及原理進行了驗證。Lazar等[15]將混聯Ⅰ型慣容系統應用到多層建筑結構,研究了慣容系統的減震性能,結果表明,慣容系統不僅可降低調諧質量、減小結構響應而且具有實現輕量化的優勢,但在結構每層都設置慣容系統會使工程造價較高。潘超等[16]將結構減震性能、成本控制同時作為設計控制目標,分析了單自由度結構慣容系統結構響應解析式,在隨機振動響應解析解的基礎上,推導了簡潔適用的參數設計公式。

由于地震過程具有隨機性,國內外學者提出一系列隨機激勵模型擬合地震過程,如白噪聲模型[17]、過濾白噪聲模型[18-19]、胡聿賢模型[20]、李鴻晶模型[21]等。其中,李鴻晶模型不僅考慮了基巖的低頻成分而且消減和控制了基巖的高頻成分,該模型不僅可以描述地震的寬帶特征亦可以描述窄帶特性,是一種普適性強的隨機激勵模型。為深入研究地震激勵對建筑結構的影響,需對結構基于隨機地震模型下的響應進行分析,常用方法為時域法及頻域法。時域法[22-23]以求解響應協方差為主,需求解激勵的協方差;頻域法[24-25]以建立響應和激勵功率譜之間的代數關系為主。相比白噪聲模型及過濾白噪聲模型而言,李鴻晶模型以功率譜函數的形式存在,且功率譜函數較為復雜,運用時域法分析較為繁瑣,頻域法分析較容易。虛擬激勵法[26]是頻域法中典型的分析方法,該方法將平穩隨機過程轉化為簡諧過程,簡化了計算過程,但該方法在求解譜矩時尚需相當繁復的數值積分。針對以上不足,Ge等[27]在此基礎上,提出了譜矩簡明封閉解的計算方法,該方法通過求解響應功率譜的二次分解式(圓頻率和模態復特征值平方和倒數的線性組合形式)將譜矩轉化為模態參數與激勵參數的線性組合,消除了復雜的積分運算且提高了計算精度。

目前針對慣容系統的研究多數基于單自由度結構展開,在多自由度結構中的應用及具體布置方案的研究較少。針對這一問題,本文運用文獻[28]所提出的計算方法,分析混聯Ⅰ型慣容系統在多自由度結構中的地震動響應,同時從性能和經濟性角度出發,對慣容系統在多自由度中的布置方案進行研究。首先,求解多自由度結構部分層設置混聯Ⅰ型慣容系統基于隨機激勵下的運動方程,并依據慣容系統的計算簡圖推導其微分型本構關系。基于此,重構運動方程,并運用復模態理論及虛擬激勵法求解結構絕對位移、層間位移、層間位移角等系列響應的統一解。其次,對結構系列響應功率譜進行了二次分解,獲得響應0～2階譜矩的簡明封閉解。最后,在響應譜矩封閉解的基礎上,通過數值算例對比驗證了所求譜矩的正確性;分析了復振型個數對結構響應譜矩計算精度的影響;確定并驗證了慣容系統布置方案的有效性。

1 重構運動方程

在n層結構的部分層設置混聯Ⅰ型慣容系統共l個(1≤l≤n)構成耗能結構,計算簡圖如圖1所示。

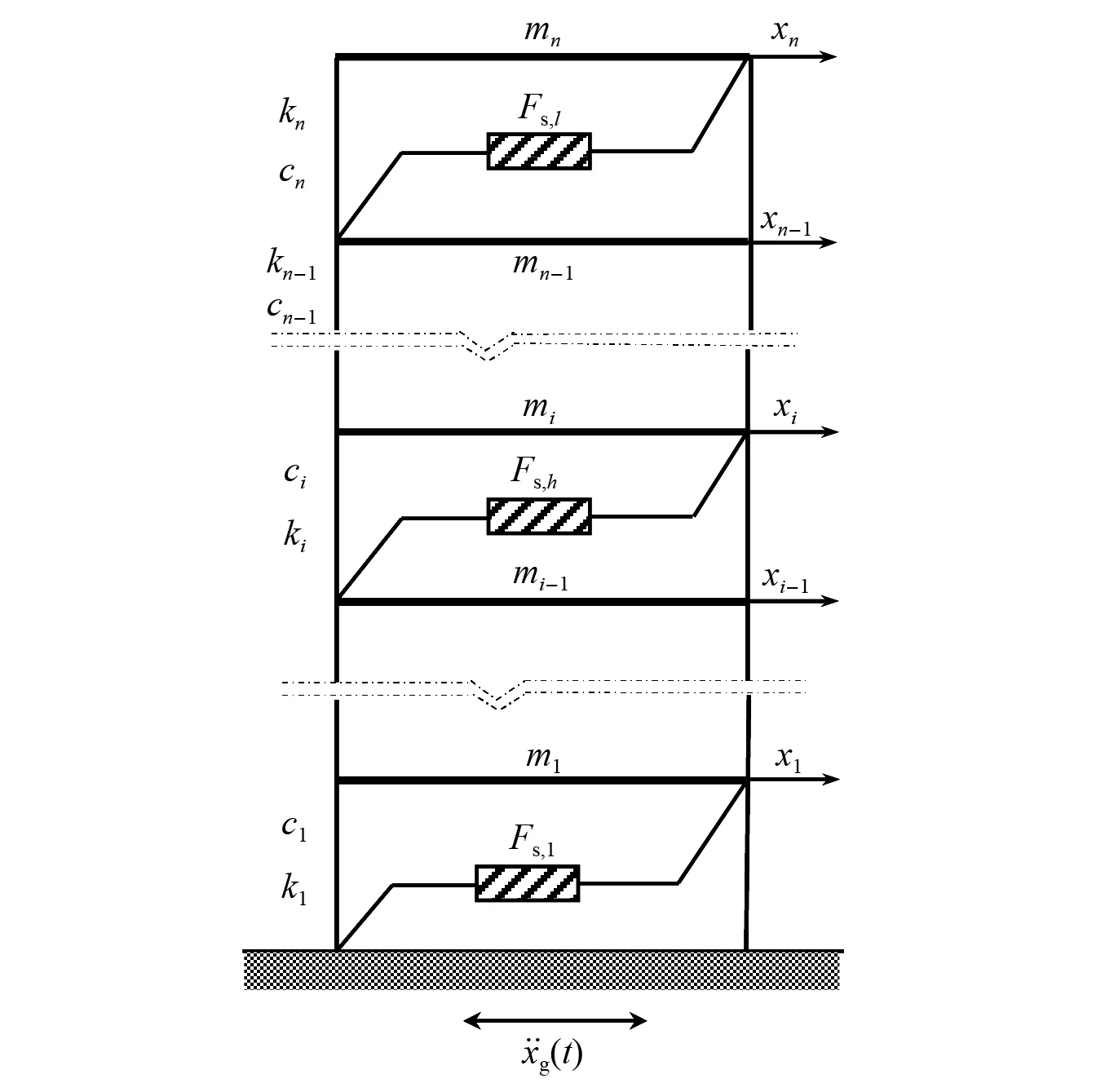
圖1 耗能結構計算簡圖Fig.1 Schematic diagram of the energy-consuming structure

(1)

當結構第1層設置第1個混聯Ⅰ型慣容系統時,計算簡圖如圖2(a)所示;當結構第i層(當i>1)設置第h個(1≤h≤l)混聯Ⅰ型慣容系統時,計算簡圖如圖2(b)所示。由圖2(a)和圖2(b)可知,存在以下力學關系

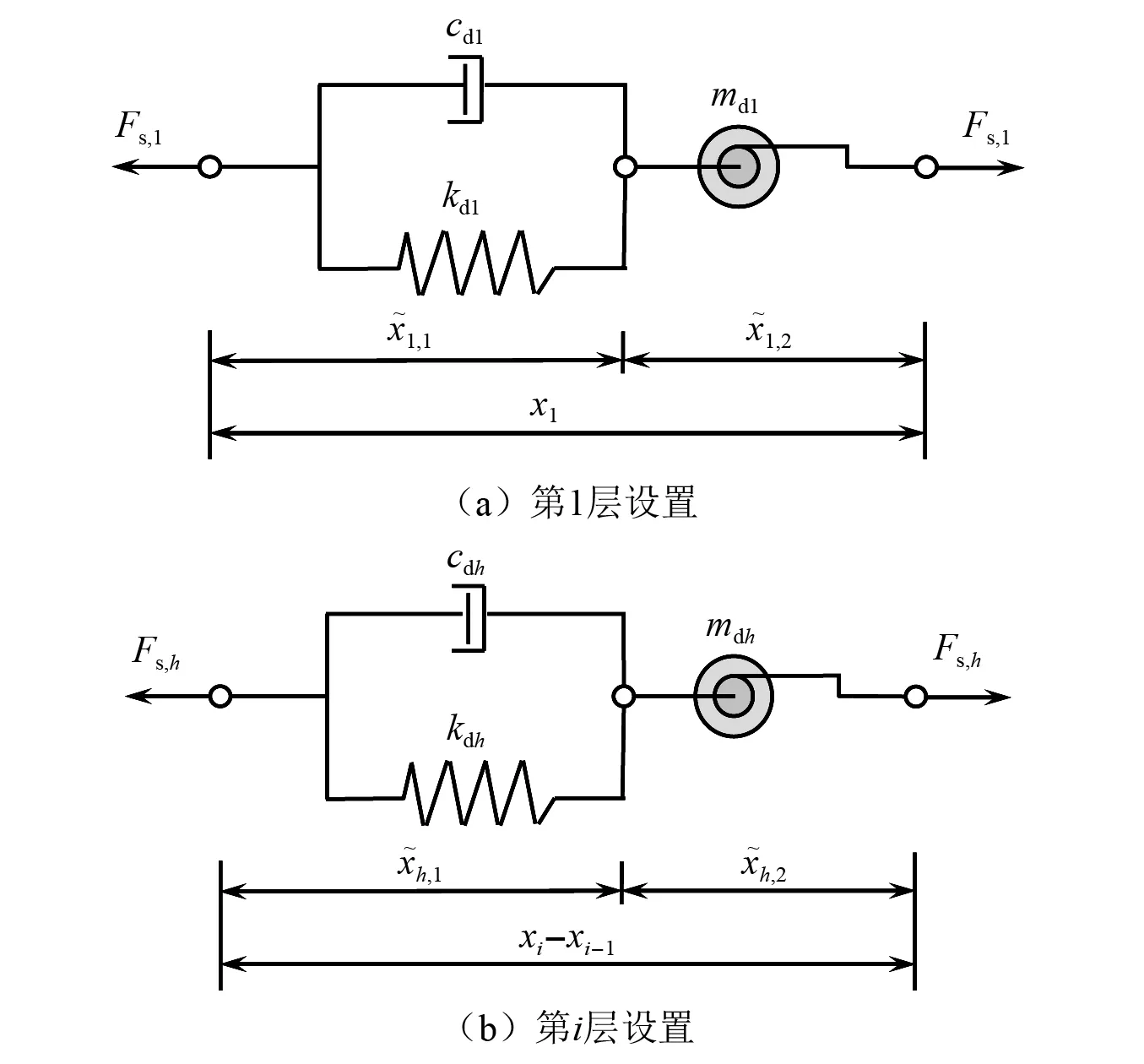
圖2 混聯Ⅰ型慣容系統的布置簡圖Fig.2 Diagram of the arrangement of series-parallel layout Ⅰ inerter system

(2)

(3)

由式(2)、式(3)可知,所設l個慣容系統的力學關系為

(4)

(5)

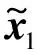
聯立式(4)、式(5),可得慣容系統與結構之間的微分型本構關系為

(6)

引入狀態變量X,聯立式(1)、式(4)～式(6)得到狀態方程為

(7)

(8)

式中:α=[-MIo4o5o4]T,“T”為轉置矩陣;o1為n×n階元素為零的矩陣;o2為n×l階元素為零的矩陣;o3為l×l階元素為零的矩陣;o4為l×1階元素為零的矩陣;o5為n×1階元素為零的矩陣;M0,K0分別為

2 結構系列響應的統一解

2.1 復模態解耦

運用復模態法對式(8)進行解耦,式(8)中存在復特征值矩陣p及左、右特征向量V,U,滿足

p=(VTM0U)-1VTK0U

(9)

引入復模態變換

X=Uz

(10)

式中,z為模態廣義變量。

聯立式(8)～式(10)可得

(11)

式中,η=VTα/(VTM0U)。

式(11)的分量形式為

(12)

式中:zk為響應分量;pk為復特征值;ηk為模態強度系數。

由虛擬激勵法獲得響應分量zk(ω)的頻域解為

(13)

2.2 響應的頻域統一解

聯立式(7)、式(8)、式(13),獲得結構第i層絕對位移和絕對速度的頻域解分別為

(14)

(15)

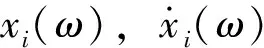
結構第i層的層間位移和層間速度頻域解分別為

(16)

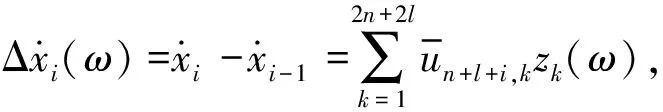
(17)

結構第i層的層間剪力為

(18)

(19)

結構第i層的層間位移角為

(20)

(21)

由式(14)～式(21)可知,結構系列響應的頻域解可統一表示為

(22)

式中:Y(ω)為結構分量zk(ω)的頻域統一解;κk為響應分量的模態系數,具體值由式(14)～式(21)確定。

3 響應功率譜及譜矩計算

3.1 結構系列響應功率譜的二次分解式

根據虛擬激勵法,結構系列響應功率譜為

(23)

將式(13)代入式(23)可得

(24)

頻率響應特征值函數HY(ω)的具體表達式為

(25)

(26)

式中:S0為譜強度系數;ωg,ξg分別為巖土層的特征頻率和阻尼比;ωs,ωh分別為基巖擾動下的低頻以及高頻控制參數。

為便于求解結構響應譜矩,將式(26)進行簡化,得到李鴻晶譜二次分解形式為

(27)

其中,

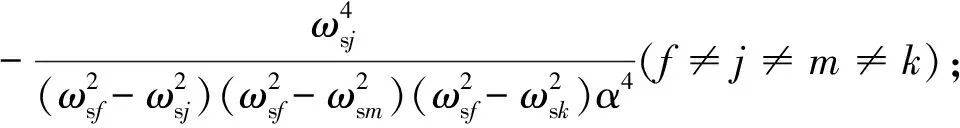
Δ1=-1-4iωsα; Δ2=-1+4iωsα。

根據代數運算將式(25)化簡為

(28)

將式(27)、式(28)代入式(24),獲得結構系列響應功率譜SY(ω)的二次分解式

(29)

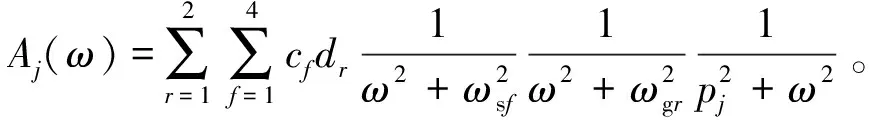
經上文分析可知,SY(ω)為響應分量對應的模態系數κk、復特征值pk、模態強度系數ηk、模態響應功率譜Aj(ω)的線性組合。

3.2 結構響應譜矩的封閉解

隨機振動理論定義譜矩為

(30)

將SY(ω)的表達式(29)代入式(30),令q=0,q=1得到0階、1階譜矩,具體表達式為

(31)

(32)

(33)

由于2階譜矩是位移變化率的0階譜矩,可有位移0階譜矩進行表示,具體表達式為

(34)

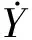
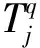
4 算例分析

一棟18層的混凝土結構,抗震設防烈度為8度,場地類別為Ⅱ類場地,場地土為中等土。1層為門廳和服務中心,2～3層用于養育托管管理配套等功能,其余樓層用于住宅。1層層高4.5 m,2～3層層高4 m,4～18層層高3 m;1層質量m1=6.5×105kg,2～3層質量m2=m3=4.9×105kg,4～18層質量為3×105kg;1層抗側剛度k1=3×108N/m,2～3層的抗側剛度k2=k3=2.15×108N/m,4～18層抗側剛度為1.63×108N/m;結構阻尼比?為0.05,主體結構的阻尼依據Rayleigh阻尼分析,即C=aM+bK,其中a,b為Rayleigh阻尼常數。

式中,ω1和ω2分別為結構的第一自振頻率和第二自振頻率,ω1=2.079 7 rad/s,ω2=6.105 5 rad/s。

混聯Ⅰ型慣容系統的主要參數依據式(35)～式(37)確定

μ=md/m

(35)

κ=kd/k

(36)

(37)

式中:μ,κ,ξ分別為慣容系統的慣質比、剛度比以及名義阻尼比;md,cd,kd分別為慣容系統的慣容系數、阻尼系數、剛度系數;m,c,k分別為主體結構的質量、阻尼、剛度;ω0為結構的自振圓頻率。

為同時滿足結構的減震性能和成本要求,需合理擬合慣容減震系統的參數。潘超等研究了單自由度結構中慣容系統同時滿足成本和性能的參數設計方法,利用所提公式及設計流程確定了混聯Ⅰ型慣容系統滿足成本和性能的優化參數值。由于多自由度慣容系統的性能-成本參數優化文獻較少,故本文選取潘超等研究中的表1(混聯Ⅰ型慣容系統的主要設計參數值),以目標阻尼比為0.04確定μ=0.085 1,κ=0.041 7,ξ=0.020 9。

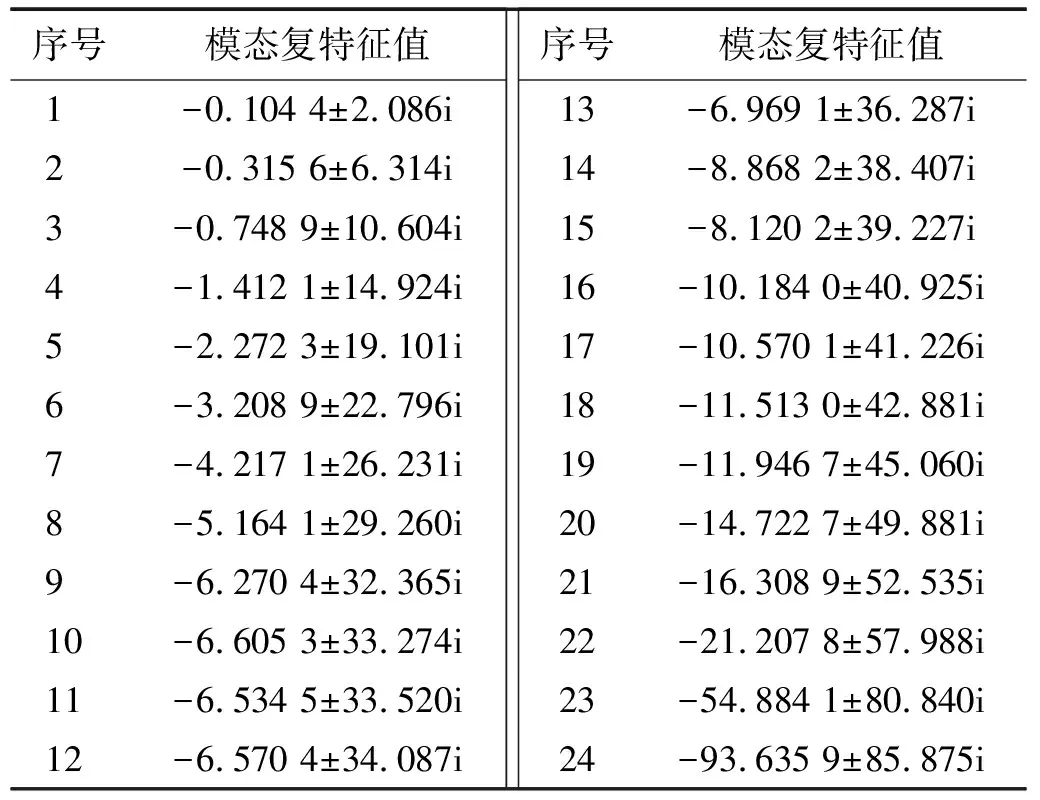
表1 結構響應模態復特征值Tab.1 Modal complex eigenvalues of response of the structure

通過式(35)～式(37)求得md=2.553×104kg,kd=6.797 1×104N/m,cd=2.923×104N·s/m。

4.1 封閉解的正確性驗證

以1層、2層、4層、8層、14層、16層設置慣容系統為例,驗證本文所求耗能結構響應譜矩封閉解式(31)～式(34)的正確性。由于虛擬激勵法是結構隨機響應分析中典型的計算方法,故將本文方法所得譜矩與虛擬激勵法所得結果進行對比驗證。

由附錄A中式(A.9)可知,虛擬激勵法求解響應譜矩需要對響應功率譜Sx(ω)在[0,∞]內進行積分運算,為獲得穩定且精確的譜矩值,經試算積分區間取[0,500]rad/s,積分步長Δω依次取2.0 rad/s,1.0 rad/s,0.5 rad/s,0.1 rad/s。本文方法與虛擬激勵法在4種不同積分步長下的譜矩對比,如圖3所示。

圖3 響應譜矩對比Fig.3 Comparison of response spectral moments

由圖3可知,本文方法直接獲得結構系列響應的譜矩,所得結果唯一、計算精確較高。虛擬激勵法所求譜矩的精確度受積分步長取值的影響較大。當積分步長Δω≥1.0 rad/s時,各樓層譜矩的誤差較大;當Δω≤0.5 rad/s時,各樓層的譜矩值逐漸趨于穩定,最終越來越接近本文方法所求結果;且當Δω=0.1 rad/s時,兩種方法所得結果誤差率小于3%。經上述分析可知,本文方法所求多自由度混聯Ⅰ型慣容系統系列響應譜矩的封閉解正確有效,在推導過程中不僅簡化了計算過程而且提高了計算精度。

4.2 復振型個數對結構響應精度的影響

由結構動力學可知,多自由度實模態分析中前若干振型對結構動力響應的影響顯著,而其他高階振型的影響較小可忽略不計。本文方法所求的振動特征值和振型為復參數,一對復共軛振動特征值和振型由歐拉變換可轉化為一個實特征值和實振型。為滿足結構動力響應的精度要求,并進一步提高本文方法的計算效率,將分析復振型對結構響應精度的影響。

由式(31)可知,本文所求譜矩值是復振動特征值與其他相關參數的線性組合。將以結構1層、2層、4層、8層、14層、16層設慣容系統為例,分析不同復振型下的響應值。表1為結構響應的模態復特征值pk,按照從小到大進行排序,將pk代入式(13),并依據式(14)～式(21)得到絕對位移、絕對速度等響應值,具體結果如圖4所示。

圖4 復振型對響應精度的影響Fig.4 Effect of mode shape on response calculation

由圖4可知,只考慮1階復振型時,所得位移、速度、層間位移角及層間剪力(所有樓層取平均值)依次占全振型的88.3%,78.0%,68.6%,60.0%;考慮前2階復振型所得以上方差平均依次占全振型的98.9%,93.2%,89.9%,88.6%;考慮前3階復振型所得以上響應方差平均依次占全振型的100.0%,98.5%,97.4%,96.2%。由此得出,復振型個數對結構位移的影響不明顯,但對結構的層間位移角等響應影響較為突出,且對剪力的影響最大。高階復振型對于較低樓層的動力響應影響較小,且前3階復振型貢獻率都超過95%。故在結構響應分析過程中,為保證計算精度、減少計算量、提高計算效率可只考慮前3階復振型。

在考慮前3階復振型的情形下,本文方法求解動力響應方差所用時間為0.094 8 s,運用傳統方法計算所需時間為15.47 s,即考慮前3階復振型具有較高的計算效率。

4.3 慣容系統布置方案的研究

在結構設計中,層間位移及層間位移角決定了結構內力和附屬結構的安全。當層間位移或層間位移角過大時,可能導致結構的開裂或損壞,從而影響結構穩定性和舒適度。為滿足結構的抗震性能和經濟要求,以減小結構的層間位移或層間位移角為目標,分析慣容系統的布置方案。依據式(16)、式(17)、式(20)、式(21)對無控結構的層間位移、層間位移角進行了計算,具體結果如圖5所示。

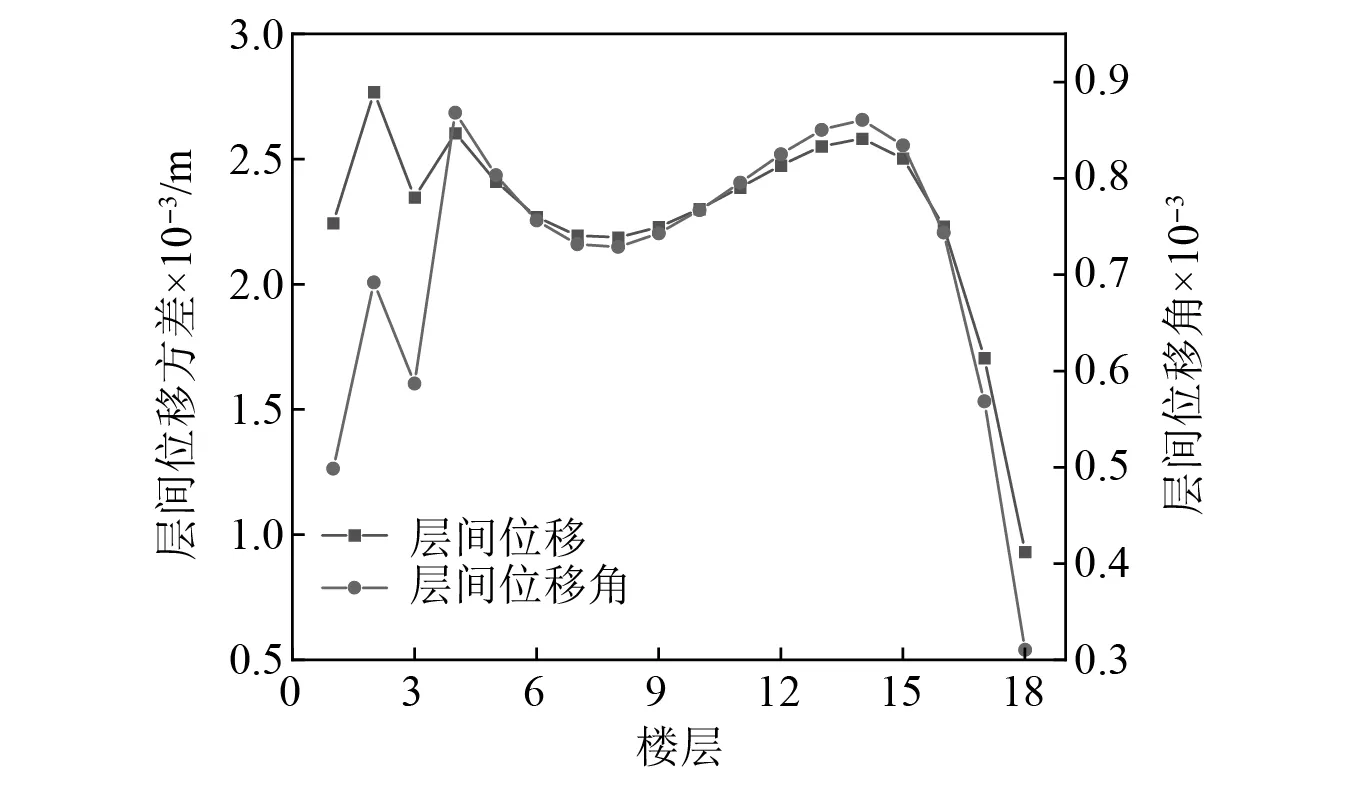
圖5 無控結構的層間位移及層間位移角Fig.5 Interstory displacement and Interstory displacement angle of uncontrolled structure

由圖5可知,在2層、4層、14層結構的層間位移、層間位移角同時出現峰值,此時對結構性能極為不利。依據層間位移、層間位移角峰值所在樓層,分別考慮其上、下層確定慣容系統在多自由度結構中的布置方案。具體方案1為1層、2層、4層、14層設置慣容系統;方案2為1層、2層、3層、4層、13層、14層、15層設置慣容系統;方案3為每層都設慣容系統。

依據式(14)～式(21)、式(31)～式(33)對各方案的位移、層間位移、層間位移角及層間剪力進行了對比計算,具體結果如圖6～圖9所示。

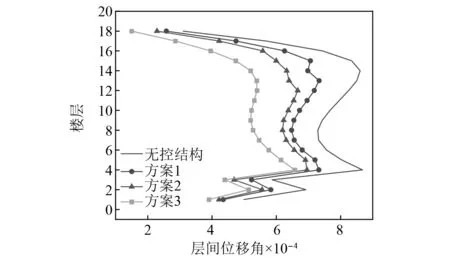
圖6 布置方案的層間位移角對比Fig.6 Comparison of interlayer displacement angles of each program

圖7 各布置方案的層間剪力對比Fig.7 Comparison of interstory shear force for each program

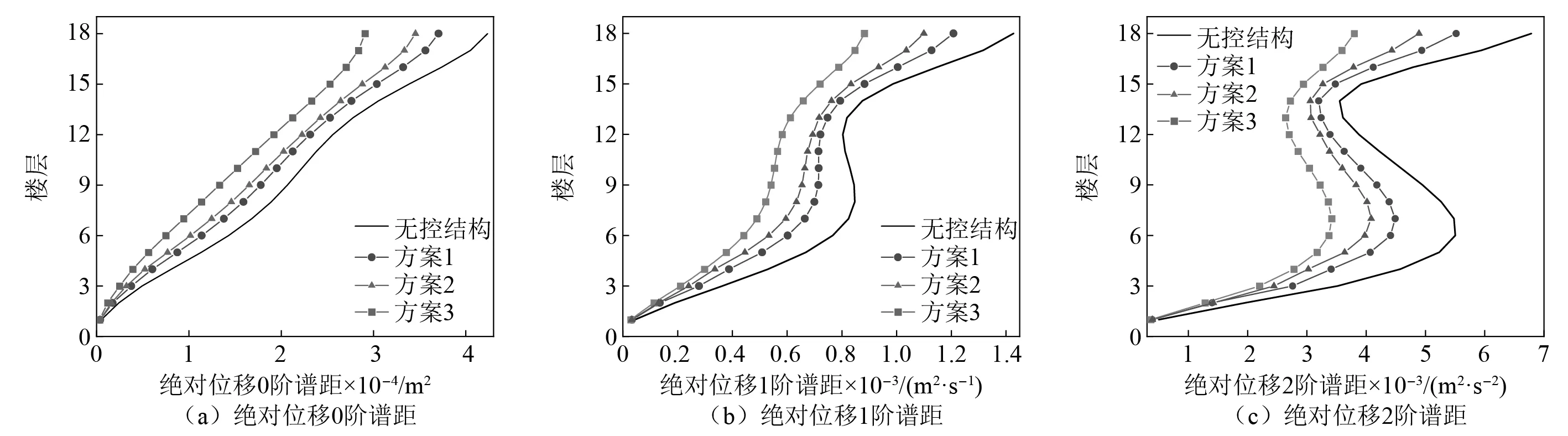
圖8 各布置方案的絕對位移0～2階譜矩對比Fig.8 Comparison of absolute displacement 0-2nd spectral moments of each program

圖9 各布置方案的層間位移0～2階譜矩對比Fig.9 Comparison of 0-2nd spectral moments of inter-story displacement of each program

由圖6～圖9可知,方案3結構每層都設置慣容系統的減震效果最為明顯,當結構中所設的慣容系統數量足夠多時,結構的性能總能達到抗震設計要求,但這種做法從經濟角度考慮是不可取的。

為更準確分析三種方案的可行性,對各方案在層間位移、層間位移角出現峰值樓層(2層、4層、14層)的減震效果進行分析,具體結果如表2所示。由表2可知:方案1對絕對位移、絕對速度、層間剪力、層間位移角、層間位移的最大減震率分別為27.3%,28.5%,34.3%,18.9%,30.9%;方案2對上述系列響應的最大減震率分別為33%,36.5%,48.3%,31.9%,46%。

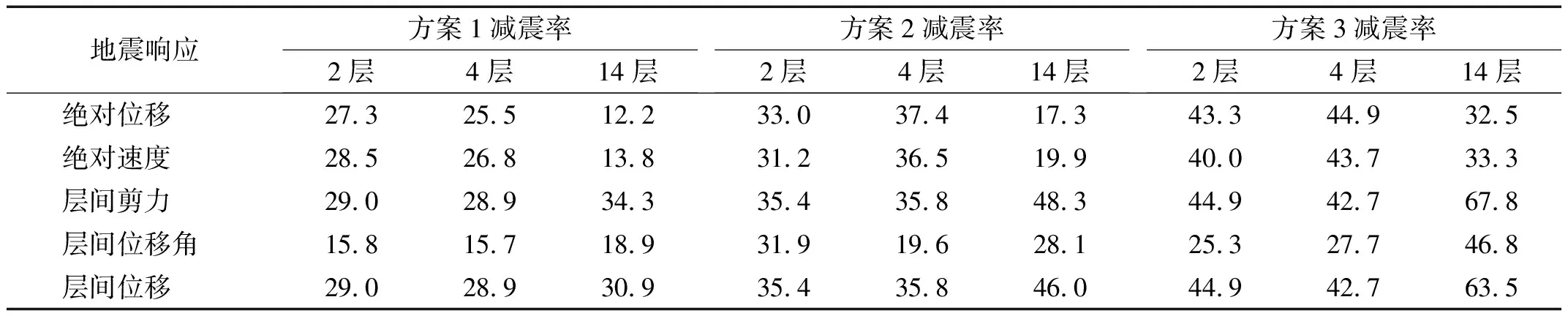
表2 各布置方案的減震效果分析Tab.2 Analysis of vibration damping effect of each program 單位:%

經上述分析可知:方案3的減震效果最好,但所需成本較高;方案2的減震效果較方案1更加明顯,且平均減震率在35%以上,能夠有效降低結構層間位移和層間位移角。

5 結 論

本文將混聯Ⅰ型慣容系統應用于多自由度結構的消能減震中,運用功率譜二次分解法給出了結構系列響應譜矩的封閉解,在結構響應0～2階譜矩封閉解的基礎上,對慣容系統在多自由度結構中的布置方案進行研究。為減小計算量、提高計算效率,本文分析了不同復振型對高層結構響應計算精度的影響。所得結論有:

(1) 本文在n層結構中設置l(1≤l≤n)個混聯Ⅰ型慣容系統,將位移、速度、層間位移角等響應的0～2階譜矩簡化為模態譜矩、復特征值及其他參數的線性組合,運用數值算例驗證了本文方法所求的譜矩正確適用。

(2) 獲得多自由度結構混聯Ⅰ型慣容系統的位移、速度等系列響應的頻域解和0～2階譜矩,對分析實際工程中結構動力可靠度如超過結構性能要求界限的平均率,首次破壞的時間及頻率分布等具有一定的工程意義。

(3) 高階復振型對位移的影響較不明顯,但對速度、層間位移角、層間剪力等響應的影響較為顯著。為準確分析和預測結構的抗震性能,高階復振型的影響不能忽略。前3階復振型對各響應的影響都在95%以上,故為簡化計算量,提高計算效率建議考慮前3階復振型。

(4) 本文在結構響應0～2階譜矩封閉解的基礎上,確定了慣容系統的布置方案。研究發現方案3減震效果最好,但整體造價較高;方案2相對方案1的減震效果較為顯著,有效降低了層間位移和層間位移角,且該方案相對方案3降低了工程造價。為滿足結構性能和經濟要求,建議將慣容系統以方案2進行布置。

附錄A:耗能結構響應譜矩的虛擬激勵法

對式(1)、式(4)、式(5)進行傅里葉變換

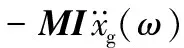
(A.1)

(A.2)

(A.3)

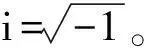
由式(A.2)、式(A.3)得到

(A.4)

(A.5)

把式(A.4)和式(A.5)代入式(A.2)則

(A.6)

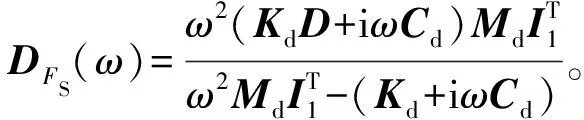
將式(A.6)代入式(A.1)得到結構絕對位移為

(A.7)

式中,Hx(ω)=-Mω2+iωC+K+I1DFS(ω)。

結構層間位移為

Δxi(ω)=xi(ω)-xi-1(ω),i=2～n

(A.8)

式中, Δx1(ω)=x1(ω)。

結構層間剪力為

V1(ω)=k1x1(ω)

(A.9)

Vi(ω)=ki[xi(ω)-xi-1(ω)],i=2～n

(A.10)

結構層間位移角為

(A.11)

(A.12)

結構位移的功率譜為

(A.13)

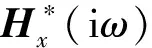
速度的功率譜為

(A.14)

層間剪力、層間位移角等響應可依據位移及速度的功率譜進行求解。

將(A.7)代入譜矩計算公式,得到絕對位移0～2階譜矩為

(A.15)