單邊約束下受脈動(dòng)內(nèi)流激勵(lì)作用簡支輸流管的碰振響應(yīng)研究

王天林, 郭長青, 漆發(fā)輝, 許 鋒, 盧小緬,方孟孟

(1. 南華大學(xué) 土木工程學(xué)院,湖南 衡陽 421001;2. 南華大學(xué) 數(shù)理學(xué)院,湖南 衡陽 421001;3. 貴州師范大學(xué) 大數(shù)據(jù)與計(jì)算機(jī)科學(xué)學(xué)院,貴陽 550025;4. 悉地國際設(shè)計(jì)顧問(深圳)有限公司,廣東 深圳 518000)

輸流管在機(jī)械化工氣力輸送系統(tǒng)[1]、航空航天液壓系統(tǒng)[2]、核工業(yè)冷卻系統(tǒng)[3]以及石油與天然氣的運(yùn)輸[4-5]等諸多領(lǐng)域中應(yīng)用廣泛。輸流管系統(tǒng)的耦合振動(dòng)(管道的結(jié)構(gòu)振動(dòng)、流體的壓力脈動(dòng)等)極易導(dǎo)致管道薄弱部位發(fā)生裂紋,繼而破裂,造成嚴(yán)重的管道安全事故,導(dǎo)致巨大的經(jīng)濟(jì)損失,如11·22青島輸油管道爆炸事件。因此,國內(nèi)外眾多學(xué)者[6-9]對(duì)輸流管的振動(dòng)穩(wěn)定性問題開展了持續(xù)性研究。輸流管運(yùn)用于實(shí)際工程中,管道內(nèi)部會(huì)因動(dòng)力裝置(如,泵、壓縮機(jī)等)的工作而產(chǎn)生脈動(dòng)內(nèi)流,導(dǎo)致輸流管發(fā)生振動(dòng)。輸流管服役期間可能會(huì)遭遇約束松動(dòng)、受工作環(huán)境限制而使輸流管與障礙物相鄰近等問題,導(dǎo)致輸流管在振動(dòng)過程中管道局部與約束發(fā)生碰撞,而碰撞振動(dòng)可能會(huì)降低管道系統(tǒng)的穩(wěn)定性、縮短管道的使用壽命。目前,輸流管與對(duì)稱約束的碰撞振動(dòng)研究已較為成熟,單邊約束碰撞振動(dòng)研究也取得了豐厚的成果,但是單邊約束與輸流管的碰撞振動(dòng)研究還較為少見,因此,很有必要針對(duì)該問題開展相應(yīng)的研究工作。

輸流管與對(duì)稱約束的碰撞振動(dòng)研究中,許多學(xué)者采用了立方非線性彈簧或修正的分段三線性彈簧模擬對(duì)稱約束。Paidoussis等[10-12]先后采用立方非線性彈簧與修正的分段三線性彈簧模擬對(duì)稱約束,分析了對(duì)稱約束下懸臂輸流管的碰撞振動(dòng)特性,并通過試驗(yàn)對(duì)數(shù)值計(jì)算結(jié)果進(jìn)行驗(yàn)證,其試驗(yàn)結(jié)果與理論預(yù)測具有較好的一致性。Wang等[13]研究了對(duì)稱約束下懸臂輸流立管的穩(wěn)定性和混沌運(yùn)動(dòng),并與Jin[14]開發(fā)的懸掛式系統(tǒng)進(jìn)行比較,發(fā)現(xiàn)懸臂輸流立管系統(tǒng)的動(dòng)力學(xué)特性比懸掛式系統(tǒng)更為豐富。唐冶等[15]研究了對(duì)稱約束下受多種激勵(lì)作用懸臂輸流管的非線性動(dòng)力學(xué)行為。Wang等[16]使用立方非線性彈簧模擬對(duì)稱約束,研究了受對(duì)稱約束作用懸臂輸流管的三維動(dòng)力學(xué)行為。

單邊約束由于約束的非對(duì)稱性,吸引了眾多學(xué)者對(duì)其開展研究。Zhang等[17]建立了單邊約束非光滑系統(tǒng)的時(shí)間積分方法框架,并通過曲柄滑塊機(jī)構(gòu)的數(shù)值試驗(yàn),驗(yàn)證了該方法比經(jīng)典的Moreau-Jean時(shí)步法所提框架在精度和效率上更具優(yōu)勢。Peng等[18]提出了一種基于辛方法和線性互補(bǔ)法求解多體碰撞接觸動(dòng)力學(xué)問題的方法,并通過多個(gè)數(shù)值案例證明所提出的方法即使在較大的時(shí)間步長下也具有較高精度。Miao等[19]對(duì)單邊約束下受簡諧激勵(lì)作用的單自由度沖擊振子進(jìn)行研究,從拓?fù)鋵W(xué)的角度研究了Nordmark映射混沌吸引子的結(jié)構(gòu)。Gritli等[20]基于OGY狀態(tài)反饋控制律,研究了單邊約束下單自由度沖擊振子的非線性動(dòng)力學(xué)行為。Reboucas等[21]采用點(diǎn)映射法、標(biāo)準(zhǔn)平均法和非光滑變換相結(jié)合的方法,分析了帶恢復(fù)系數(shù)單自由度模型的振動(dòng)沖擊響應(yīng)。Guo等[22]研究了單邊剛性約束下受簡諧激勵(lì)作用的雙擺模型。通過引入碰撞恢復(fù)矩陣、模態(tài)分析和矩陣?yán)碚?得到了高維非光滑非對(duì)稱系統(tǒng)中單邊雙碰撞周期解的解析表達(dá)式。

目前,只有極少數(shù)的學(xué)者對(duì)單邊約束與輸流管的碰撞振動(dòng)問題開展研究,王乙坤等[23]基于碰撞恢復(fù)系數(shù)構(gòu)造了輸流管與單邊剛性約束碰撞前后管道各處狀態(tài)向量的傳遞矩陣,分析了間隙值和碰撞恢復(fù)系數(shù)對(duì)輸流管系統(tǒng)的影響。

本文對(duì)單邊約束下受脈動(dòng)內(nèi)流激勵(lì)作用簡支輸流管的碰振響應(yīng)問題開展研究。首先,通過Hamilton原理推導(dǎo)出輸流管系統(tǒng)的運(yùn)動(dòng)微分方程。其次,使用Galerkin法將偏微分方程離散為常微分方程組。最后,采用可變階次的數(shù)值微分(numerical differentiation formulas,NFDs)算法[24-25]對(duì)離散后的常微分方程組進(jìn)行求解。研究了脈動(dòng)內(nèi)流激勵(lì)頻率、平均流速、單邊約束位置坐標(biāo)與約束間隙等參數(shù)對(duì)輸流管系統(tǒng)的影響規(guī)律,為輸流管的碰撞振動(dòng)控制提供理論基礎(chǔ)。

1 求解方法

圖1為簡支輸流管與單邊約束的碰撞振動(dòng)模型。當(dāng)輸流管與單邊約束發(fā)生碰撞時(shí),單邊約束對(duì)輸流管有約束反力;輸流管與單邊約束分離后,單邊約束不再影響輸流管的運(yùn)動(dòng)。目前,已有學(xué)者[26]采用碰撞恢復(fù)系數(shù)來處理單邊約束,但使用該方法需滿足兩個(gè)條件:根據(jù)結(jié)構(gòu)的特點(diǎn)和單邊約束的位置坐標(biāo)將管道劃分為多個(gè)單元且單邊約束處于某一單元節(jié)點(diǎn)上;實(shí)際發(fā)生振動(dòng)的自由節(jié)點(diǎn)個(gè)數(shù)等于Galerkin模態(tài)截?cái)鄶?shù)。因此,當(dāng)單邊約束位置坐標(biāo)發(fā)生變化時(shí),需重新劃分單邊、Galerkin離散與構(gòu)造傳遞矩陣,極大地增加了工作量。本文新提出的非線性彈簧(受拉時(shí)剛度幾乎為零、受壓后剛度迅速增大)模型,可在不增加工作量的前提下分析單邊約束任意位置坐標(biāo)對(duì)輸流管系統(tǒng)的影響規(guī)律。

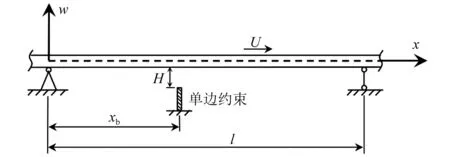
圖1 單邊約束下簡支輸流管示意圖Fig.1 Schematic diagram of simply supported fluid conveying pipe with unilateral constraints

考慮輸流管運(yùn)動(dòng)過程中因軸線變形而導(dǎo)致的幾何非線性因素,根據(jù)Hamilton原理,可將單邊約束下受脈動(dòng)內(nèi)流激勵(lì)作用簡支輸流管的運(yùn)動(dòng)微分方程寫成[27-28]

(1)

式(1)中,脈動(dòng)流的表達(dá)式[29]

U=U0[1+μsin(Ωt)]

(2)

式中:U為管內(nèi)流體的流速;U0為管內(nèi)流體的平均流速;Ω為脈動(dòng)內(nèi)流的脈動(dòng)頻率;μ為脈動(dòng)內(nèi)流的脈動(dòng)幅值。

式(1)中,等效單邊約束非線性彈簧恢復(fù)力Fb與變形量(w+H)的關(guān)系為

Fb=kb[e-s(w+H)+ζ](w+H)

(3)

式中:kb的作用是降低非線性彈簧受拉階段產(chǎn)生的恢復(fù)力;s與非線性彈簧恢復(fù)力的變化速率相關(guān),s越大則非線性彈簧受壓階段恢復(fù)力的增大速率越快;ζ的作用是確保非線性彈簧無負(fù)剛度情況;H為輸流管與約束之間的間隙。

引入如下無量綱參數(shù)

可將式(1)～式(3)寫成如下的無量綱形式

(4)

其中,

u=u0[1+μsin(ωτ)]

(5)

fb=κb[e-ν(η+h)+ζ](η+h)

(6)

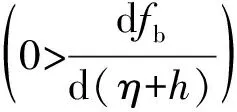
使用Galerkin法對(duì)無量綱運(yùn)動(dòng)方程式(4)、式(6)進(jìn)行離散,輸流管的橫向位移函數(shù)可表示為

(7)

式中:N為Galerkin截?cái)鄶?shù);φj(ξ)為簡支輸流管(簡支梁)第j階的振型函數(shù);Tj(τ)為廣義坐標(biāo),且有

φj=sin(λjξ)

(8)

λj滿足特征方程

λj=jπ

(9)

φ={φ1,φ2,…,φN},T={T1,T2,…,TN}T

(10)

將式(7)代入式(4)和式(6),并在方程兩邊同時(shí)左乘φT,再對(duì)ξ從0～1積分,由模態(tài)函數(shù)的正交性,輸流管的運(yùn)動(dòng)微分方程可離散成如下形式

(11)

其中,

(12)

(13)

(14)

pb=2κbφ(ξb)T{e-ν[φ(ξb)T+h]+ζ}[φ(ξb)T+h]

(15)

(16)

(17)

p=pb-pE-pα

(18)

為了方便后續(xù)的數(shù)值計(jì)算,引入狀態(tài)向量

(19)

將式(11)寫成如下形式的一階狀態(tài)方程

(20)

(21)

式中:I為N階的單位矩陣;Ok為N階的零矩陣;Op為向量分量為0的N維列向量。

式(20)為單邊約束下受脈動(dòng)內(nèi)流激勵(lì)作用簡支輸流管的非線性控制常微分方程組,求解該方程組可獲得輸流管在取定參數(shù)下的動(dòng)力響應(yīng)。

2 計(jì)算結(jié)果驗(yàn)證與分析

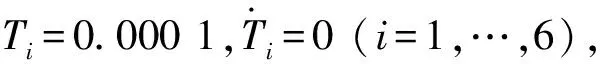
輸流管單邊約束處(ξ=ξb)分岔圖的觸發(fā)條件為該處的速度趨于零,即

(22)

同理,可得輸流管中點(diǎn)處(ξ=0.5)分岔圖的觸發(fā)條件為

(23)

分別記錄下滿足式(21)與式(22)條件時(shí),輸流管單邊約束處(ξ=ξb)的位移η(ξb,τ)與中點(diǎn)處(ξ=0.5)的位移η(0.5,τ)。

2.1 脈動(dòng)激勵(lì)頻率的影響

為驗(yàn)證本文算法的正確性,在不考慮單邊約束情況時(shí),采用王乙坤等研究中的參數(shù)(N=5,u0=4.5,α=0.005,β=0.64,κ=5 000,μ=0.2),本文采用NFDs算法得到的以脈動(dòng)激勵(lì)頻率ω為控制參數(shù)輸流管中點(diǎn)處的分岔圖(如圖3(a)所示)與王乙坤采用四階Runge-Kutta法所得圖像(圖3(b)所示)一致,表明本文算法是可靠的。

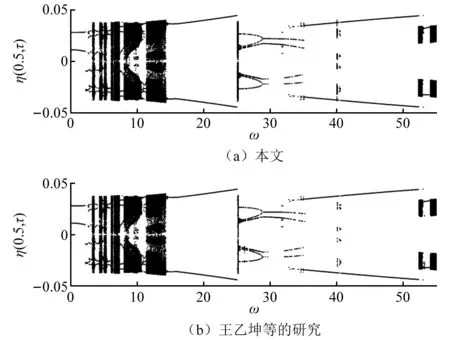
圖3 以脈動(dòng)激勵(lì)頻率ω為控制參數(shù)輸流管中點(diǎn)處的分岔圖Fig.3 With pulsating internal flow excitation frequency ω is used as the control parameter of the bifurcation diagram at the midpoint of fluid conveying pipe

圖4是以脈動(dòng)激勵(lì)頻率為控制參數(shù)輸流管單邊約束處與中點(diǎn)處的分岔圖,結(jié)合Poincare映射圖(由于篇幅限制未繪制在文中)可得系統(tǒng)由穩(wěn)定周期運(yùn)動(dòng)通向混沌窗口與由混沌窗口演化穩(wěn)定周期運(yùn)動(dòng)的演化路徑。當(dāng)17.6≥ω≥7.7時(shí),隨著ω的不斷增大,系統(tǒng)的運(yùn)動(dòng)形態(tài)由周期-2(本文周期-N1為不發(fā)生碰撞的周期N1運(yùn)動(dòng),周期N1為發(fā)生碰撞的周期N1運(yùn)動(dòng),周期N1運(yùn)動(dòng)為系統(tǒng)做穩(wěn)態(tài)周期運(yùn)動(dòng),且其運(yùn)動(dòng)周期為N1倍脈動(dòng)激勵(lì)周期)因發(fā)生碰撞振動(dòng)而直接進(jìn)入第一個(gè)混沌窗口,而后由混沌運(yùn)動(dòng)經(jīng)倒倍周期分岔(周期2n、周期2n-1、…、周期8、周期4、周期2)演化為穩(wěn)定的周期2。當(dāng)25.4≥ω≥21.6時(shí),系統(tǒng)由周期2直接通向第二個(gè)混沌窗口,而后由混沌運(yùn)動(dòng)經(jīng)倒倍周期分岔(周期3×2n、周期3×2n-1、…、周期12、周期6、周期3)演化為穩(wěn)定的周期3。當(dāng)43.6≥ω≥43.5時(shí),系統(tǒng)由周期3直接進(jìn)入第三個(gè)混沌窗口。

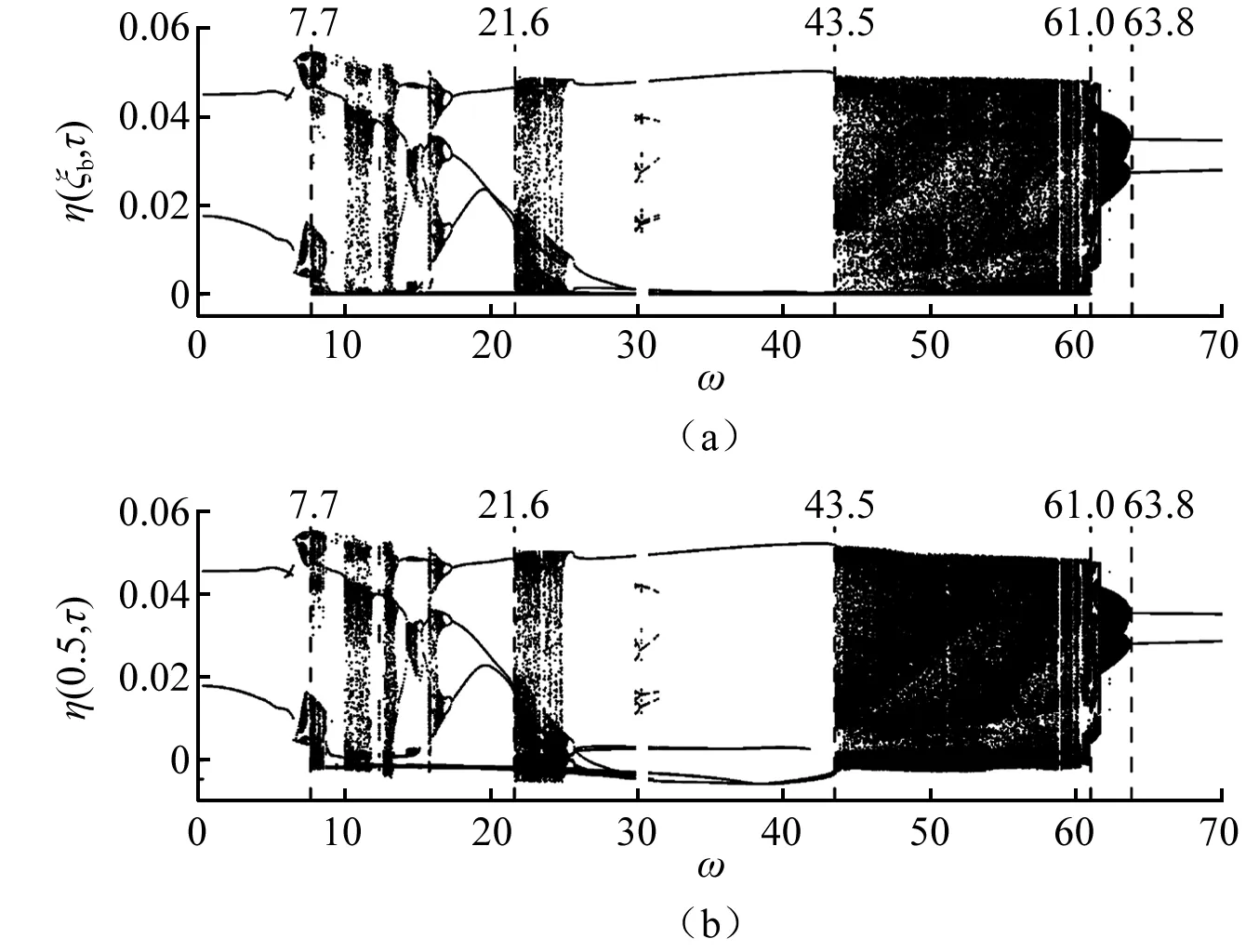
圖4 以脈動(dòng)激勵(lì)頻率ω為控制參數(shù)輸流管單邊約束處和 中點(diǎn)處的分岔圖Fig.4 With pulsating internal flow excitation frequency ω is used as the control parameter of the bifurcation diagram at the unilateral constraint and midpoint of fluid conveying pipe

當(dāng)ω≥61時(shí),系統(tǒng)將不再發(fā)生碰撞振動(dòng)。若繼續(xù)增大ω,當(dāng)ω≥63.8時(shí),脈動(dòng)激勵(lì)頻率將不再影響系統(tǒng)的運(yùn)動(dòng)形態(tài),系統(tǒng)將一直保持周期-1。

當(dāng)ω處于系統(tǒng)發(fā)生碰撞振動(dòng)的脈動(dòng)激勵(lì)頻率范圍時(shí),系統(tǒng)可由穩(wěn)定周期運(yùn)動(dòng)直接進(jìn)入混沌窗口,而后又由混沌運(yùn)動(dòng)經(jīng)倒倍周期分岔演化為穩(wěn)定的周期運(yùn)動(dòng)。

2.2 平均流速的影響

圖5是以平均流速為控制參數(shù)輸流管單邊約束處與中點(diǎn)處的分岔圖,可以觀察到當(dāng)3.16≥u0時(shí),系統(tǒng)不發(fā)生振動(dòng)。當(dāng)4.56>u0>3.16時(shí),系統(tǒng)幾乎處于非碰撞振動(dòng)狀態(tài)。

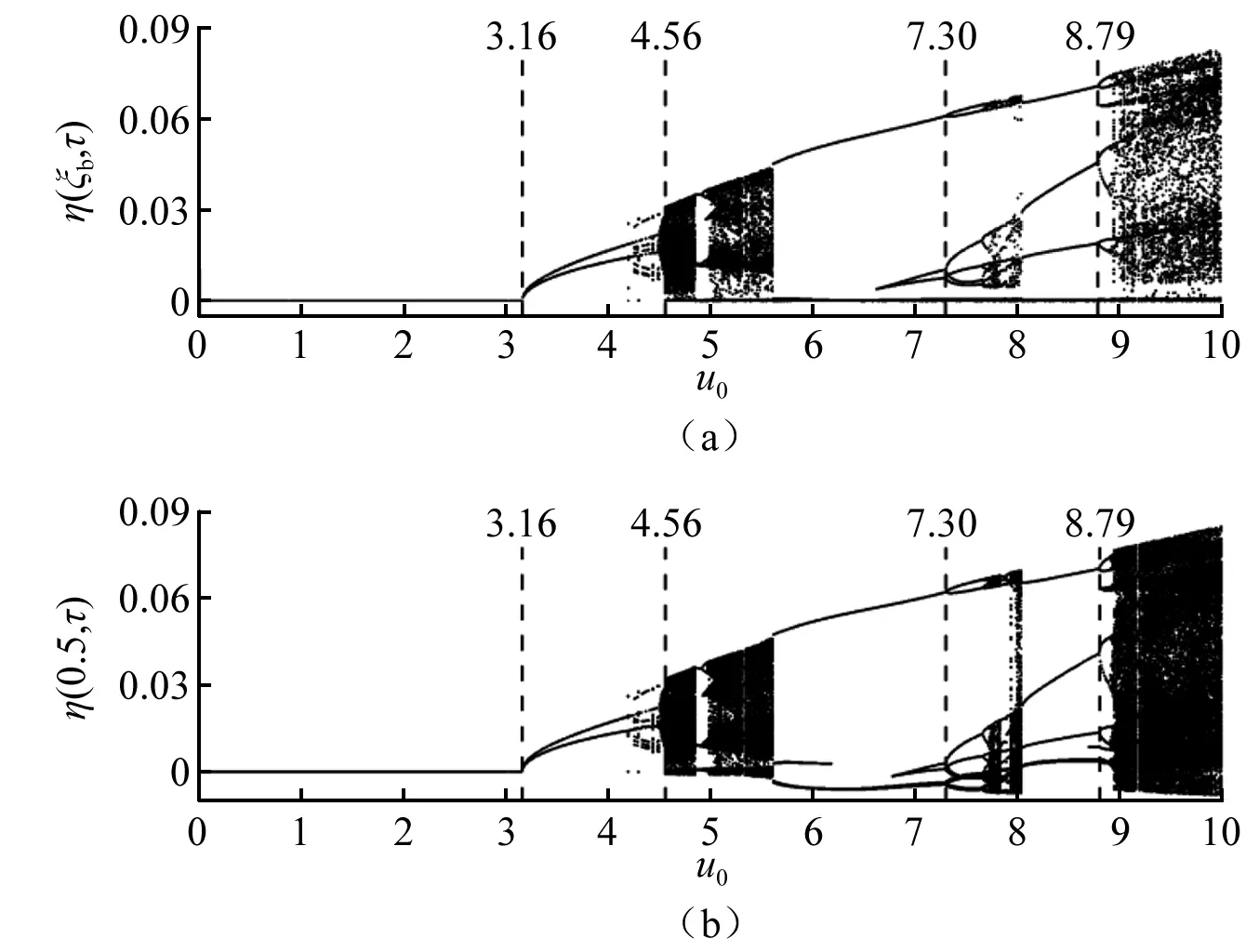
圖5 以平均流速u0為控制參數(shù)輸流管單邊約束處 和中點(diǎn)處的分岔圖Fig.5 With the average flow velocity u0 is used as the control parameter of the bifurcation diagram at the constraint and midpoint of fluid conveying pipe

當(dāng)5.62≥u0≥4.5時(shí),隨著u0的增大,系統(tǒng)的運(yùn)動(dòng)形態(tài)由周期-1經(jīng)穩(wěn)定焦點(diǎn)、吸引圓、概周期運(yùn)動(dòng),最后因發(fā)生碰撞振動(dòng)而進(jìn)入混沌窗口,此過程Poincare映射圖的演化[30]如圖6所示。圖6(a)為隨運(yùn)動(dòng)時(shí)間的增大Poincare映射圖呈順時(shí)針螺旋匯聚成穩(wěn)定焦點(diǎn)的過程;繼續(xù)增大u0,Poincare映射圖將呈現(xiàn)先順時(shí)針螺旋匯聚,到達(dá)轉(zhuǎn)向點(diǎn)(順時(shí)針螺旋匯聚與逆時(shí)針螺旋匯聚的分界點(diǎn))后,逆時(shí)針螺旋匯聚成穩(wěn)定焦點(diǎn),如圖6(b);若再繼續(xù)增大u0,Poincare映射圖將呈現(xiàn)先順時(shí)針螺旋匯聚,到達(dá)轉(zhuǎn)向點(diǎn)后逆時(shí)針螺旋匯聚成吸引圓,且吸引圓隨著u0的增大而不斷向外擴(kuò)張,最終演變?yōu)橐环忾]曲線,此時(shí)系統(tǒng)的運(yùn)動(dòng)形態(tài)為概周期運(yùn)動(dòng),該過程Poincare射圖的演化如圖6(c)～圖6(e);當(dāng)u0≥4.56時(shí),輸流管與約束發(fā)生碰撞振動(dòng)導(dǎo)致封閉曲線崩潰,系統(tǒng)進(jìn)入混沌窗口,其后系統(tǒng)直接由混沌運(yùn)動(dòng)跳躍為周期3而離開混沌窗口。

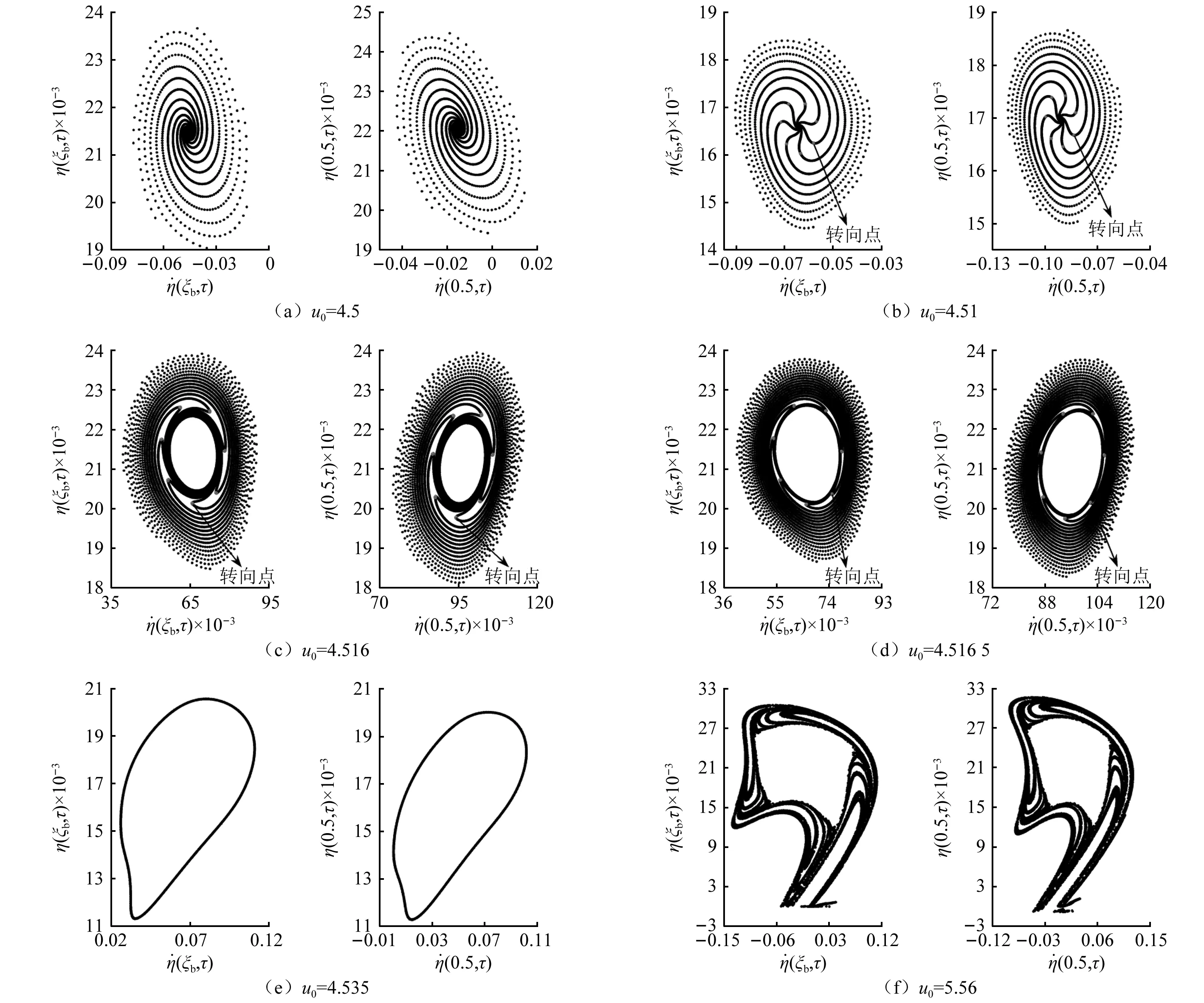
圖6 輸流管單邊約束處與中點(diǎn)處的Poincare映射圖Fig.6 Poincare map at unilateral constraint and midpoint of pipe conveying fluid

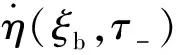
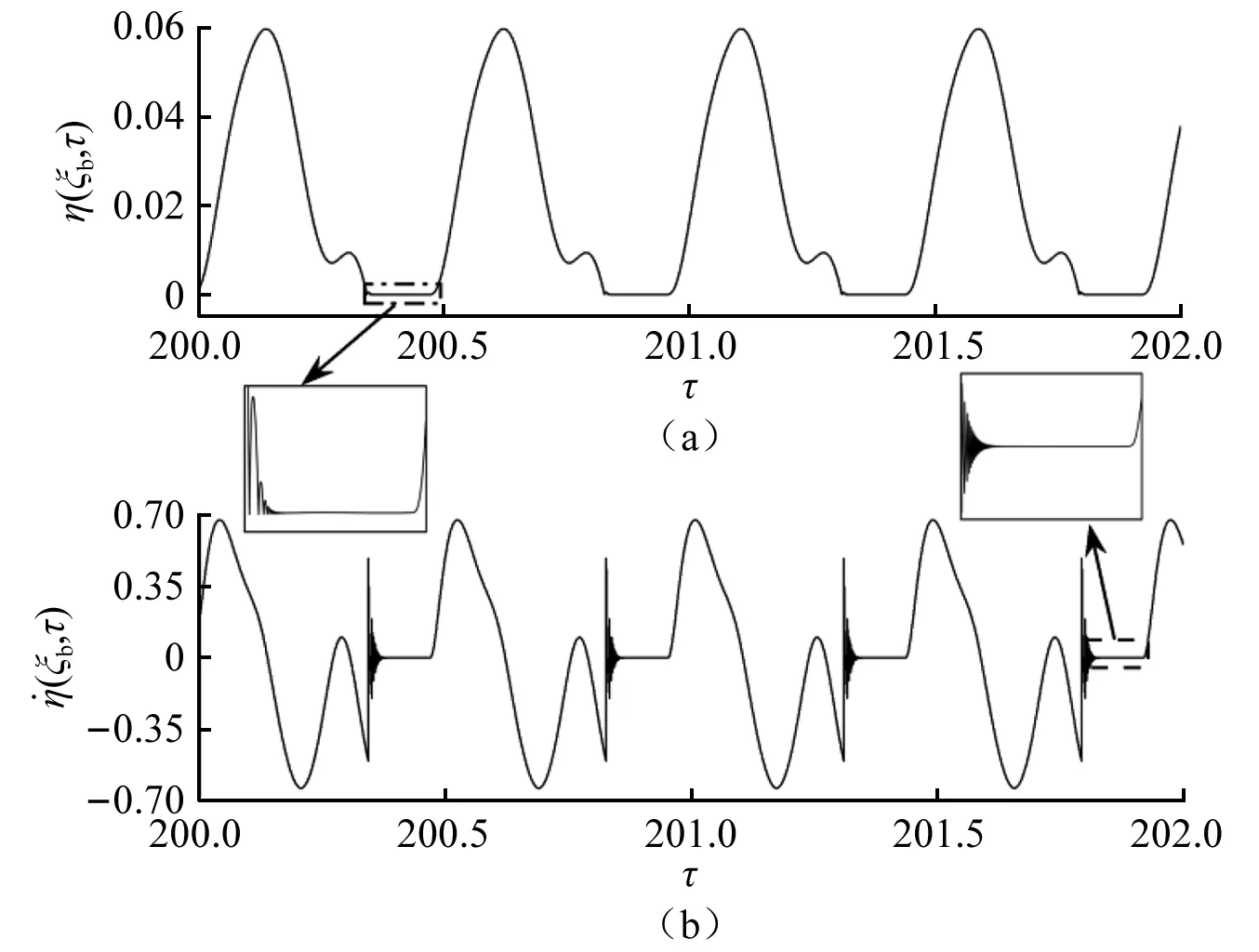
圖7 輸流管單邊約束處的位移時(shí)程曲線與速度時(shí)程 曲線(u0=7.2)Fig.7 Displacement time history curve and velocity time history curve at the unilateral constraint of the flow tube(u0=7.2)

從圖7觀察到系統(tǒng)出現(xiàn)周期性完全顫碰振動(dòng)[31-32],單邊約束下受脈動(dòng)內(nèi)流激勵(lì)的簡支輸流管在此運(yùn)動(dòng)過程中經(jīng)歷三種運(yùn)動(dòng)狀態(tài):參數(shù)振動(dòng)(本文參數(shù)振動(dòng)狀態(tài)只受脈動(dòng)內(nèi)流激勵(lì)作用不碰撞振動(dòng))、顫碰振動(dòng)和黏滯狀態(tài)。系統(tǒng)處于顫碰振動(dòng)時(shí),輸流管約束處的振動(dòng)幅值與沖擊速度(輸流管撞擊單邊約束時(shí)管道單邊約束處的速度)隨著碰撞次數(shù)的增加而不斷減小,但在減小為零之前,輸流管約束處的合力方向發(fā)生改變,系統(tǒng)未能進(jìn)入黏滯狀態(tài)的顫碰振動(dòng)稱為周期性非完全顫碰振動(dòng);將沖擊速度減小為零時(shí),輸流管約束處合力仍然指向單邊約束,導(dǎo)致輸流管與單邊約束黏滯在一起,合力方向發(fā)生改變后,輸流管與單邊約束分離,黏滯狀態(tài)結(jié)束的顫碰振動(dòng)被稱為周期性完全顫碰振動(dòng)。

當(dāng)8.05≥u0≥7.3時(shí),系統(tǒng)由周期3經(jīng)倍周期分岔(周期3、周期6、…、周期3×2n)通向混沌窗口,而后又由混沌運(yùn)動(dòng)跳躍為周期3離開混沌窗口。當(dāng)8.95≥u0≥8.79時(shí),系統(tǒng)由周期3經(jīng)倍周期分岔(周期3、周期6、…、周期3×2n)通向混沌窗口。

通過對(duì)管內(nèi)流體平均流速的研究,觀察到了周期性完全顫碰振動(dòng);發(fā)現(xiàn)了輸流管系統(tǒng)通向混沌的兩種路徑:由穩(wěn)定周期運(yùn)動(dòng)經(jīng)穩(wěn)定焦點(diǎn)、吸引圓、概周期運(yùn)動(dòng)通向混沌窗口與由穩(wěn)定周期運(yùn)動(dòng)經(jīng)倍周期分岔通向混沌窗口。

2.3 單邊約束位置坐標(biāo)的影響

2.3.1 無約束間隙系統(tǒng)(h=0)

圖8是以單邊約束的位置坐標(biāo)ξb為控制參數(shù)輸流管單邊約束處與中點(diǎn)處的分岔圖,從該圖可以清楚地觀察到當(dāng)單邊約束處于始端支座附近(0.173≥ξb>0)時(shí),輸流管與單邊約束一直處于黏滯狀態(tài)。

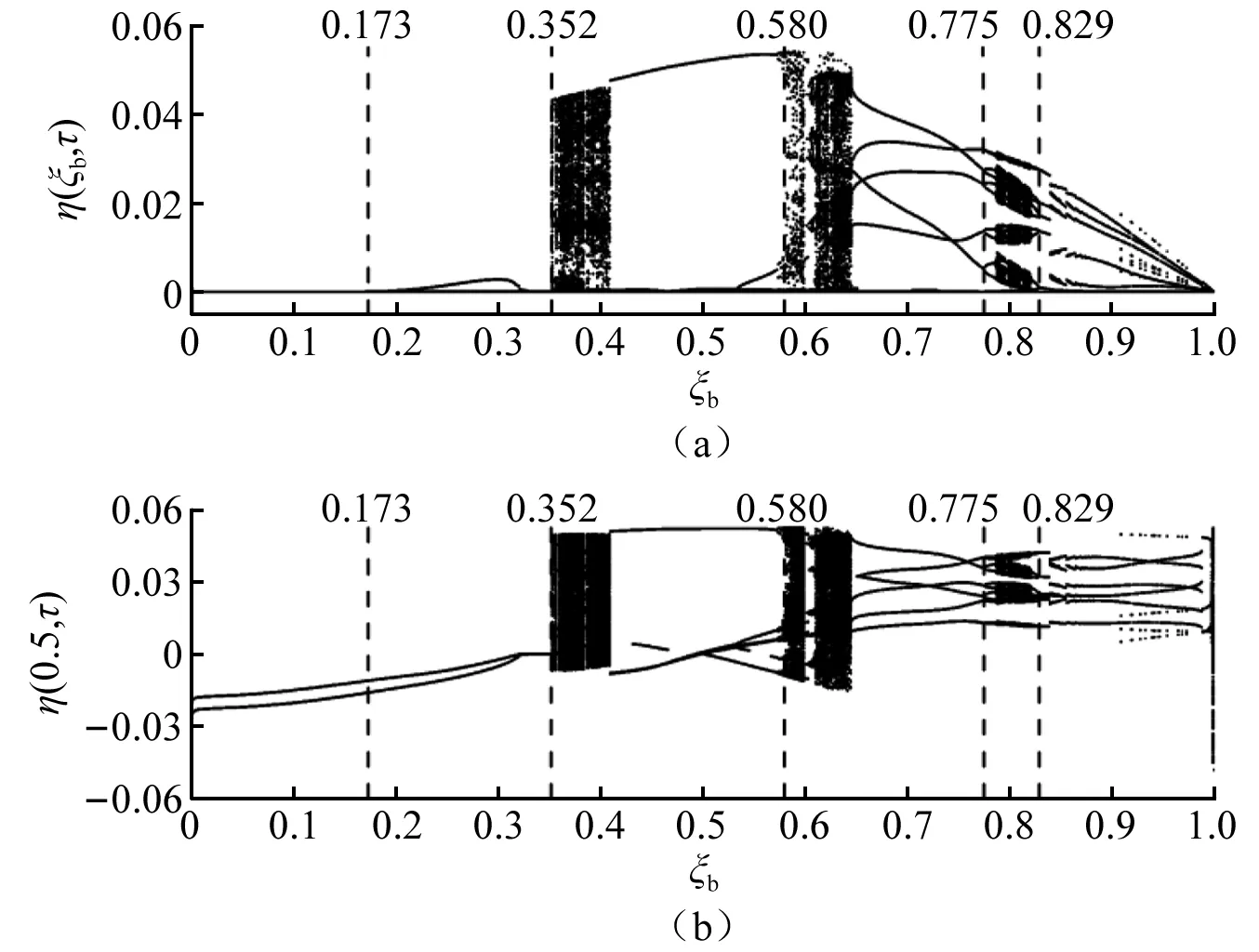
圖8 以約束的位置坐標(biāo)ξb為控制參數(shù)輸流管單邊 約束處和中點(diǎn)處的分岔圖(h=0)Fig.8 The position coordinate of the constraint ξb is used as the control parameter of the bifurcation diagram at the unilateral constraint and midpoint of fluid conveying pipe (h=0)

當(dāng)0.829≥ξb≥0.775時(shí),系統(tǒng)出現(xiàn)周期N1的一種特殊碰撞振動(dòng)形態(tài)——N2/N1周期碰撞振動(dòng),即系統(tǒng)歷經(jīng)N1個(gè)脈動(dòng)激勵(lì)周期,輸流管與約束發(fā)生的碰撞次數(shù)為N2次的現(xiàn)象。為了更清楚地觀察輸流管與約束的N2/N1周期碰撞振動(dòng)現(xiàn)象,圖9～圖12繪制出了輸流管單邊約束處與中點(diǎn)處的相圖以及Poincare映射圖(輸流管單邊約束處相圖中的虛線表示單邊約束)。當(dāng)ξb=0.775時(shí),如圖9所示,由Poincare映射圖可知系統(tǒng)歷經(jīng)了3個(gè)脈動(dòng)激勵(lì)周期,相圖顯示輸流管與約束發(fā)生了1次碰撞,為1/3周期碰撞振動(dòng)。隨著ξb的增大,系統(tǒng)由1/3周期碰撞振動(dòng)經(jīng)倍周期碰振響應(yīng)(1/3周期碰撞振動(dòng)(見圖9所示)、2/6周期碰撞振動(dòng)(如圖10所示)、4/12周期碰撞振動(dòng)(見圖11所示)、…、2n/3×2n周期碰撞振動(dòng))通向混沌窗口(如圖12所示),而后由混沌運(yùn)動(dòng)經(jīng)倒倍周期碰振響應(yīng)(2n/3×2n周期碰撞振動(dòng)、2n-1/3×2n-1周期碰撞振動(dòng)、…、4/12周期碰撞振動(dòng)、2/6周期碰撞振動(dòng)、1/3周期碰撞振動(dòng))演化為穩(wěn)定的1/3周期碰撞振動(dòng)。

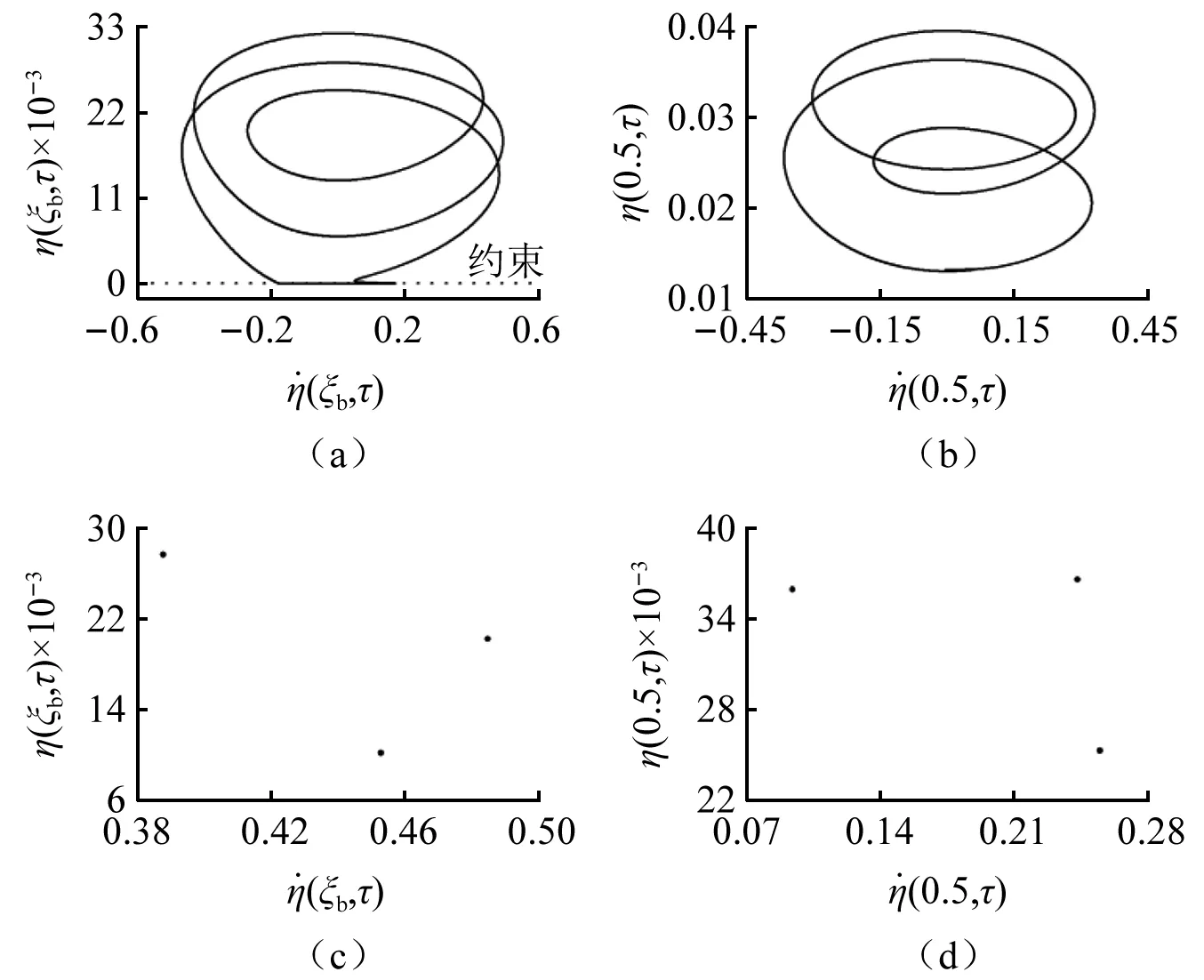
圖9 1/3周期碰撞振動(dòng)(ξb=0.775)Fig.9 1/3 periodic impact vibration (ξb=0.775)

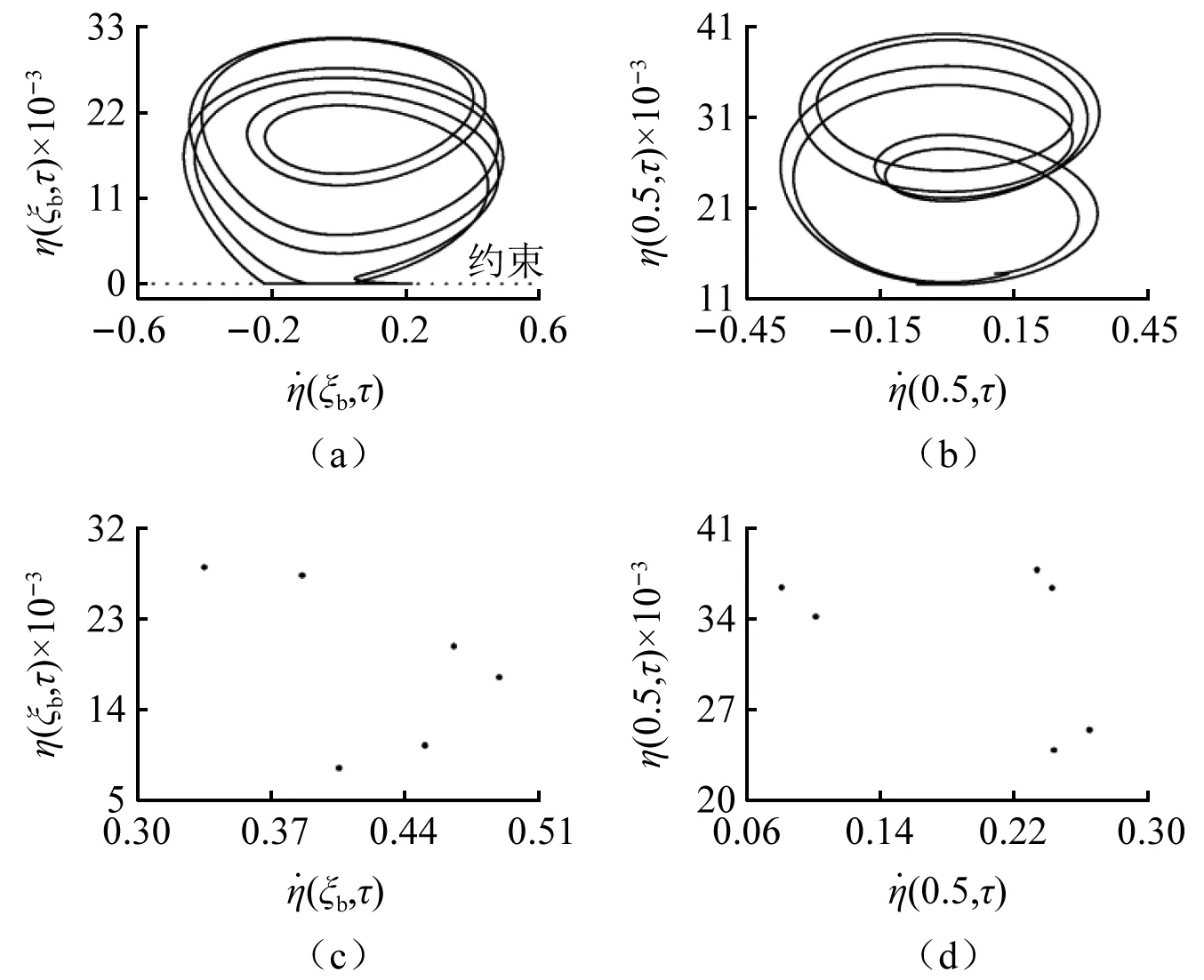
圖10 2/6周期碰撞振動(dòng)(ξb=0.785)Fig.10 2/6 periodic impact vibration (ξb=0.785)

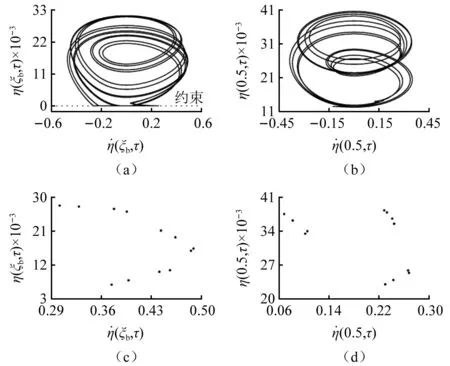
圖11 4/12周期碰撞振動(dòng)(ξb=0.787)Fig.11 4/12 periodic impact vibration (ξb=0.787)

由此可知,對(duì)于無約束間隙輸流管系統(tǒng),當(dāng)單邊約束鄰近始端支座時(shí),輸流管與單邊約束會(huì)一直處于黏滯狀態(tài),即不發(fā)生振動(dòng)。觀察到了N2/N1周期碰撞振動(dòng)現(xiàn)象與系統(tǒng)由穩(wěn)定的N2/N1周期碰撞振動(dòng)經(jīng)倍周期碰振響應(yīng)通向混沌窗口的現(xiàn)象。

2.3.2 具有約束間隙的輸流管系統(tǒng)(h=0.03)

圖13是以約束的位置坐標(biāo)ξb為控制參數(shù)輸流管單邊約束處與中點(diǎn)處的分岔圖,可以觀察到當(dāng)單邊約束處于輸流管中部(0.678>ξb>0.272)時(shí),可使系統(tǒng)的最大響應(yīng)幅值大幅度降低。結(jié)合圖8與圖13可以觀察到,輸流管單邊約束處與中點(diǎn)處的運(yùn)動(dòng)形態(tài)基本一致,由此可知,整個(gè)輸流管都處于同一運(yùn)動(dòng)形態(tài)。可能由于流體流速具有方向性,所以以約束的位置坐標(biāo)ξb為控制參數(shù)的分岔圖未關(guān)于管道中心點(diǎn)的垂線(ξb=0.5)對(duì)稱。

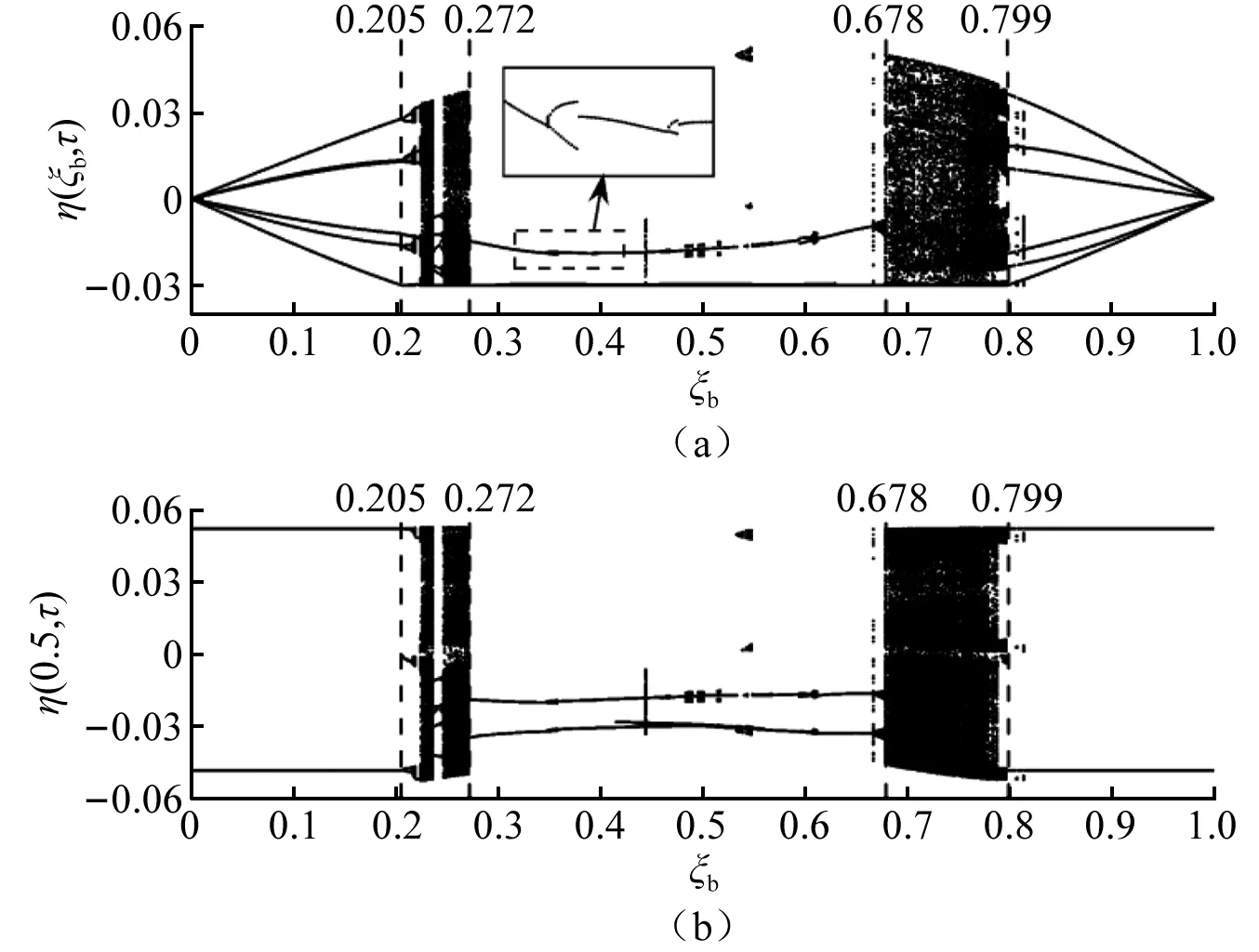
圖13 以約束的位置坐標(biāo)ξb為控制參數(shù)輸流管單邊 約束處與中點(diǎn)處的分岔圖 (h=0.03)Fig.13 The position coordinate of the constraint ξb is used as the control parameter of the bifurcation diagram at the unilateral constraint and midpoint of fluid conveying pipe (h=0.03)

從圖13可以觀察到,ξb過小輸流管會(huì)因始端支座的影響而無法與單邊約束發(fā)生碰撞振動(dòng),但此約束間隙下,隨著ξb的不斷增大,系統(tǒng)終將由非碰撞振動(dòng)經(jīng)擦邊運(yùn)動(dòng)[33-34]發(fā)生碰撞振動(dòng)。通過分岔圖結(jié)合相圖與Poincare映射圖(篇幅限制只繪制部分關(guān)鍵節(jié)點(diǎn)的圖像)可觀察到,當(dāng)0.226≥ξb≥0.205時(shí),隨著ξb的增大,系統(tǒng)的運(yùn)動(dòng)形態(tài)由周期-4、周期-4擦邊、1/4周期碰撞振動(dòng)、倍周期碰撞振動(dòng)響應(yīng)(1/4周期碰撞振動(dòng)、2/8周期碰撞振動(dòng)、…、2n/4×2n周期碰撞振動(dòng))、概周期碰撞振動(dòng)、周期-4、概周期碰撞振動(dòng),最后通向混沌窗口。

當(dāng)0.4≥ξb≥0.34時(shí),隨著ξb的增大,系統(tǒng)先后發(fā)生兩次擦邊運(yùn)動(dòng)導(dǎo)致其運(yùn)動(dòng)形態(tài)由1/1周期碰撞振動(dòng)經(jīng)一系列運(yùn)動(dòng)形態(tài)的演變,最終演化為3/1周期碰撞振動(dòng)。此過程系統(tǒng)運(yùn)動(dòng)形態(tài)的演化為:1/1周期碰撞振動(dòng)(如圖14所示)、1/1擦邊周期碰撞運(yùn)動(dòng)(如圖15所示)、概周期碰撞振動(dòng)、3/2周期碰撞振動(dòng)、2/1周期碰撞振動(dòng)(如圖16所示)、2/1擦邊周期碰撞運(yùn)動(dòng)、6/2周期碰撞運(yùn)動(dòng)、最后演化為3/1周期碰撞振動(dòng)(圖17)。

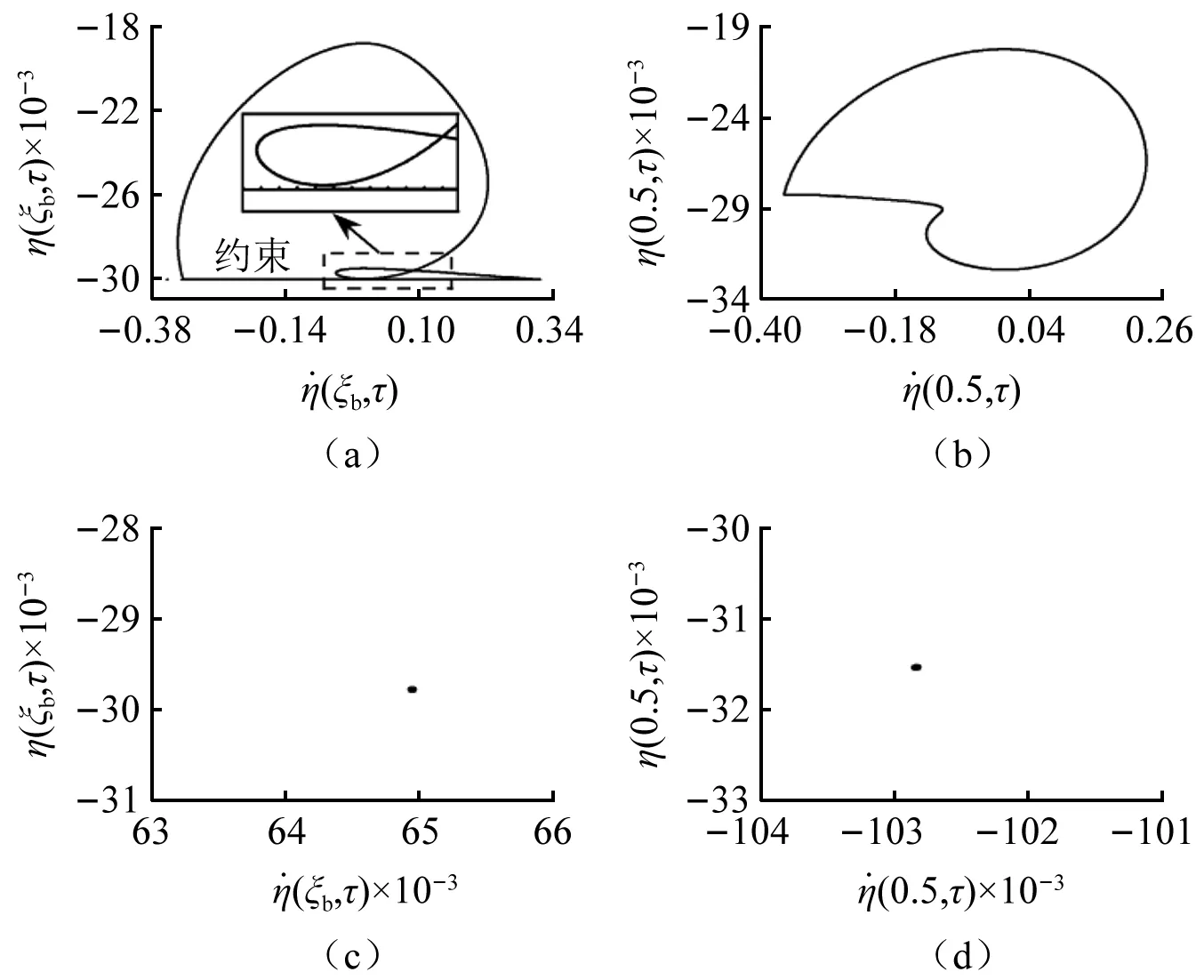
圖15 1/1擦邊周期碰撞振動(dòng)(ξb=0.345)Fig.15 1/1 grazing periodic impact vibration (ξb=0.345)

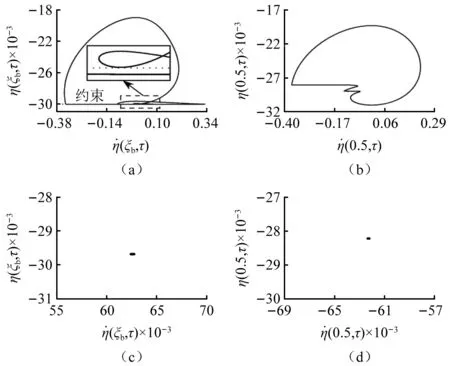
圖16 2/1擦邊周期碰撞振動(dòng)(ξb=0.3907)Fig.16 2/1 grazing periodic impact vibration (ξb=0.3907)

當(dāng)0.815>ξb≥0.786時(shí),隨著ξb的增大,輸流管的運(yùn)動(dòng)受末端支座的影響越來越大,最終將導(dǎo)致系統(tǒng)由碰振運(yùn)動(dòng)演化為非碰振運(yùn)動(dòng)。此過程系統(tǒng)的運(yùn)動(dòng)形態(tài)的演化為:混沌運(yùn)動(dòng)、1/4周期碰撞振動(dòng)、周期-4擦邊、周期-4。雖然當(dāng)ξb≥0.799,輸流管已開始不與約束發(fā)生碰撞振動(dòng),但系統(tǒng)仍會(huì)出現(xiàn)間歇性的碰撞振動(dòng),直至ξb≥0.815,輸流管才無法再與約束發(fā)生碰撞振動(dòng)。此后,系統(tǒng)的運(yùn)動(dòng)形態(tài)將一直維持周期-4。

由此可見,對(duì)于具有約束間隙的輸流管系統(tǒng),當(dāng)單邊約束處于輸流管中部時(shí),可使系統(tǒng)的最大響應(yīng)幅值大幅度降低。擦邊運(yùn)動(dòng)可誘發(fā)系統(tǒng)發(fā)生倍周期碰振響應(yīng)或使系統(tǒng)的碰振形態(tài)發(fā)生跳躍,系統(tǒng)可由碰振混沌運(yùn)動(dòng)經(jīng)周期性碰撞振動(dòng)、擦邊運(yùn)動(dòng)演化為穩(wěn)定的周期性非碰振運(yùn)動(dòng)。

3 結(jié) 論

(1) 單邊約束下受脈動(dòng)激勵(lì)作用的簡支輸流管存在三種路徑通向混沌:由穩(wěn)定的周期運(yùn)動(dòng)經(jīng)穩(wěn)定焦點(diǎn)、吸引圓、概周期運(yùn)動(dòng)通向混沌窗口;由穩(wěn)定的周期運(yùn)動(dòng)發(fā)生倍周期分岔通向混沌窗口;直接由穩(wěn)定的周期運(yùn)動(dòng)跳躍進(jìn)入混沌窗口。

(2) 對(duì)于具有約束間隙的系統(tǒng),當(dāng)單邊約束處于管道中部時(shí),約束使輸流管的最大響應(yīng)幅值大幅度降低;對(duì)于無約束間隙系統(tǒng),當(dāng)單邊約束處于始端支座附近時(shí),輸流管與約束一直處于黏滯狀態(tài)而不發(fā)生振動(dòng)。

(3) 觀察到系統(tǒng)歷經(jīng)N1個(gè)脈動(dòng)激勵(lì)周期發(fā)生N2次碰撞的N2/N1周期碰撞振動(dòng)、倍周期碰振響應(yīng)、周期性完全顫碰振動(dòng)與擦邊運(yùn)動(dòng)等非光滑碰振系統(tǒng)特有的現(xiàn)象。

(4) 擦邊運(yùn)動(dòng)可誘發(fā)系統(tǒng)發(fā)生倍周期碰振響應(yīng)或使系統(tǒng)的運(yùn)動(dòng)形態(tài)發(fā)生跳躍,系統(tǒng)可由混沌運(yùn)動(dòng)經(jīng)周期性碰撞振動(dòng)、擦邊運(yùn)動(dòng)演化為穩(wěn)定的周期性非碰振運(yùn)動(dòng)。