輪軌接觸彈性約束下動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)振動(dòng)特性分析

周生通, 謝陽(yáng)泉, 肖 乾, 陳道云, 朱海燕

(1.華東交通大學(xué) 載運(yùn)工具與裝備教育部重點(diǎn)實(shí)驗(yàn)室,南昌 330013;2.華東交通大學(xué) 軌道交通基礎(chǔ)設(shè)施性能監(jiān)測(cè)與保障國(guó)家重點(diǎn)實(shí)驗(yàn)室,南昌 330013)

近年來(lái),隨著我國(guó)高速鐵路的快速發(fā)展,國(guó)內(nèi)動(dòng)車組列車的營(yíng)運(yùn)速度已普遍提速到300 km/h左右,部分線路實(shí)現(xiàn)了常態(tài)化350 km/h高標(biāo)運(yùn)營(yíng),而最新研制的復(fù)興號(hào)高速綜合檢測(cè)列車更是在2022年4月21日濟(jì)南至鄭州高鐵濮陽(yáng)至鄭州段跑出了單列435 km/h的速度,為我國(guó)400 km/h等級(jí)的高速動(dòng)車組列車順利研制提供重要支撐。作為車輛最終承力部件,動(dòng)車輪對(duì)不但像拖車輪對(duì)一樣承受來(lái)自車體、轉(zhuǎn)向架傳遞來(lái)的全部靜動(dòng)載荷,確保車輛沿鋼軌安全走行,還要傳遞來(lái)自牽引驅(qū)動(dòng)裝置的驅(qū)動(dòng)力矩,是一個(gè)典型的同時(shí)存在彎曲、扭轉(zhuǎn)和軸向變形的高速轉(zhuǎn)子部件,具有復(fù)雜的彎扭軸振動(dòng)特性。事實(shí)上,在高速運(yùn)行環(huán)境下,動(dòng)力輪對(duì)系統(tǒng)持續(xù)受到來(lái)自輪軌接觸、齒輪嚙合以及軸箱軸承等產(chǎn)生的高頻沖擊振動(dòng)作用,然而這些高頻激勵(lì)在傳統(tǒng)的忽略柔性的輪對(duì)剛體模型中是難以被有效考慮的[1]。另一方面,高速帶來(lái)的輪對(duì)轉(zhuǎn)子高速旋轉(zhuǎn),使得動(dòng)力輪對(duì)系統(tǒng)的旋轉(zhuǎn)陀螺效應(yīng)變得更加顯著,系統(tǒng)模態(tài)信息也更加豐富[2,3]。因此,在高速列車動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)的振動(dòng)特性研究中,充分考慮輪對(duì)的柔性、旋轉(zhuǎn)陀螺效應(yīng)及其約束彈性對(duì)準(zhǔn)確把握其動(dòng)力學(xué)特性具有重要意義。

列車在軌道上高速行駛時(shí),構(gòu)成動(dòng)力輪對(duì)系統(tǒng)的輪對(duì)、齒輪、軸承等零部件均承受著從車體、鋼軌等各方面?zhèn)鬟f過(guò)來(lái)的靜、動(dòng)作用力,動(dòng)力輪對(duì)系統(tǒng)從本質(zhì)上形成了一個(gè)復(fù)雜的具有彈性變形的動(dòng)力學(xué)系統(tǒng),而全面把握這一系統(tǒng)的動(dòng)力學(xué)行為,要求能夠正確建立充分反映輪對(duì)振動(dòng)特性的精細(xì)動(dòng)力學(xué)模型。在傳統(tǒng)軌道車輛系統(tǒng)動(dòng)力學(xué)中,輪對(duì)通常被模擬為剛體,但剛性輪對(duì)僅適用于低頻范圍(0～30 Hz)內(nèi)的動(dòng)力學(xué)研究[4,5]。然而,研究發(fā)現(xiàn)自下而上傳遞的輪軌相互作用力中還包含大量的高頻激勵(lì),相較于傳統(tǒng)的剛性輪對(duì)動(dòng)力學(xué)模型,考慮輪對(duì)柔性的動(dòng)力學(xué)模型更符合高速列車的實(shí)際運(yùn)行情況[6]。目前,關(guān)于柔性輪對(duì)的建模方法主要有集總參數(shù)法[7]、連續(xù)體法[8]、傳遞矩陣法[9]、假設(shè)模態(tài)法[10]等。但這些輪對(duì)建模方法都對(duì)模型進(jìn)行了較大程度上的簡(jiǎn)化和等效,無(wú)法保證模型的完整性和分析的準(zhǔn)確性。事實(shí)上,隨著有限元技術(shù)的發(fā)展和成熟,適用于復(fù)雜結(jié)構(gòu)和邊界的有限單元法在輪對(duì)建模中逐漸被關(guān)注和應(yīng)用。當(dāng)前,構(gòu)建輪對(duì)的有限元模型主要有實(shí)體模型與梁模型兩種。其中實(shí)體模型多是借助有限元軟件以實(shí)體單元離散,然后導(dǎo)入多體動(dòng)力學(xué)軟件(如SIMPACK、UM等)中進(jìn)行輪對(duì)剛?cè)狁詈隙囿w動(dòng)力學(xué)仿真研究[11],但實(shí)體模型計(jì)算成本昂貴且在軟件仿真時(shí)難以考慮輪對(duì)旋轉(zhuǎn)陀螺效應(yīng)。相比之下,梁?jiǎn)卧M在滿足計(jì)算精度的同時(shí)還具有計(jì)算效率高的特點(diǎn),在考慮其他因素時(shí)單元整合也更為簡(jiǎn)便。因此,以梁?jiǎn)卧M輪對(duì)的方式也得到了不少學(xué)者的青睞。在基于梁理論的輪對(duì)建模方面,Liu等[12]以有限元實(shí)體模型結(jié)果為參照,對(duì)比研究了基于歐拉伯努利梁和鐵木辛柯梁的傳遞矩陣方法,發(fā)現(xiàn)考慮剪切效應(yīng)的鐵木辛柯梁能更好地反映輪對(duì)的動(dòng)力學(xué)固有特性。另一方面,針對(duì)高速運(yùn)行下的輪對(duì)陀螺效應(yīng),楊柳[13]、王滋昊等[14]基于轉(zhuǎn)子動(dòng)力學(xué)有限元理論以梁?jiǎn)卧绞綐?gòu)建了輪對(duì)的有限元模型,并分別針對(duì)機(jī)車牽引傳動(dòng)系統(tǒng)的振動(dòng)模態(tài)分析、偏心狀態(tài)下輪對(duì)轉(zhuǎn)子動(dòng)力學(xué)響應(yīng)等問(wèn)題開(kāi)展研究。不過(guò),現(xiàn)有基于梁理論的輪對(duì)轉(zhuǎn)子動(dòng)力學(xué)特性研究中,輪對(duì)梁轉(zhuǎn)子模型大多止步于描述彎曲振動(dòng)的四自由度梁模型,但能夠同時(shí)描述彎扭、彎軸和彎扭軸等耦合振動(dòng)特性的五自由度和六自由度梁模型采用較少,使得全自由度下輪對(duì)動(dòng)力學(xué)特性研究不足。

此外,高速運(yùn)行的動(dòng)力輪對(duì)轉(zhuǎn)子受到來(lái)自輪軌接觸和軸箱軸承的彈性約束作用。在非線性瞬態(tài)動(dòng)力學(xué)研究中,這些約束彈性的作用大多被簡(jiǎn)化為非線性激勵(lì)力予以考慮[15],但在振動(dòng)特性研究中則需合理等效線性化為彈簧阻尼元件[16]。例如:王滋昊等在模擬某輪對(duì)-車軸系統(tǒng)時(shí)就將軸承所在的彈性支承簡(jiǎn)化為了彈簧阻尼單元,但在固有特性和臨界轉(zhuǎn)速研究中未考慮輪軌接觸彈性的影響;楊柳等[17]則采用有限元思想將非線性的輪軌作用力和軸承約束力轉(zhuǎn)化為相應(yīng)的彈簧阻尼單元矩陣。不過(guò),在輪軌接觸彈性約束方面,現(xiàn)有研究大多僅考慮了輪軌接觸對(duì)車輪法向(即垂直于車軸方向)的彈性限制,忽略了車輪踏面錐度引起的軸向接觸彈性。

綜上所述,本文聚焦現(xiàn)有輪對(duì)轉(zhuǎn)子系統(tǒng)在振動(dòng)特性建模與仿真中的不足,在充分考慮輪對(duì)柔性、陀螺效應(yīng)和約束彈性的基礎(chǔ)上,以典型高速列車動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)為研究對(duì)象,建立基于鐵木辛柯梁轉(zhuǎn)子有限元理論的動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)彎扭軸有限元模型,推導(dǎo)出模擬輪軌約束彈性的線性化有限單元,并詳細(xì)探討動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)的彎曲、扭轉(zhuǎn)和軸向振動(dòng)特性規(guī)律以及典型外部激勵(lì)作用下動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)的共振穩(wěn)定性問(wèn)題。

1 動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)有限元模型

1.1 動(dòng)力輪對(duì)結(jié)構(gòu)離散與方程建立

如圖1所示,高速列車動(dòng)力輪對(duì)轉(zhuǎn)子部分主要由左右車輪(含輪盤(pán))、車軸和牽引大齒輪組成,并通過(guò)位于左右兩側(cè)的輪軌關(guān)系和軸箱軸承分別與鋼軌和轉(zhuǎn)向架結(jié)構(gòu)相接。為了研究動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)的振動(dòng)特性,將軸箱軸承外圈和鋼軌視作固定約束,以梁轉(zhuǎn)子有限元思想進(jìn)行結(jié)構(gòu)離散,其中,車軸結(jié)構(gòu)離散為梁轉(zhuǎn)子單元,并在軸肩、車輪、軸承、齒輪等位置離散網(wǎng)格;車輪和齒輪結(jié)構(gòu)等效為剛性圓盤(pán)單元,附在對(duì)應(yīng)位置節(jié)點(diǎn)上;輪軌接觸和軸箱軸承的約束彈性則以線性化的彈簧阻尼單元模擬。離散后的動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)有限元模型如圖2所示,其中OXYZ為整體坐標(biāo)系,Z軸沿輪對(duì)軸線方向、Y軸沿輪對(duì)垂向、X沿輪對(duì)縱向。

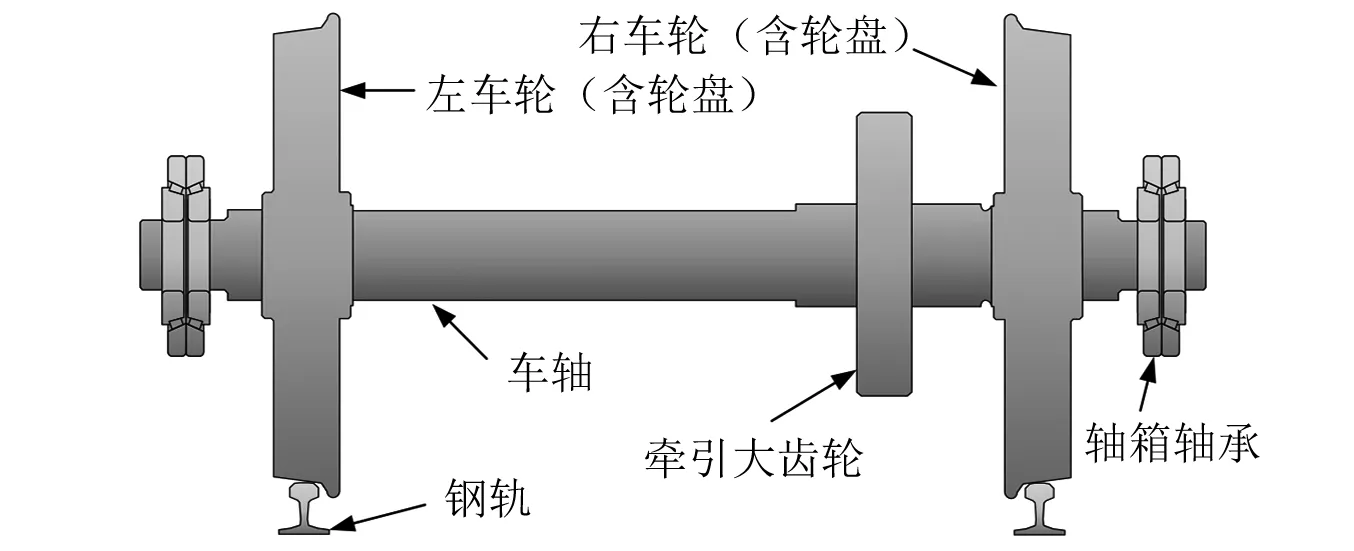
圖1 動(dòng)力輪對(duì)結(jié)構(gòu)示意圖Fig.1 Structure diagram of power wheelset

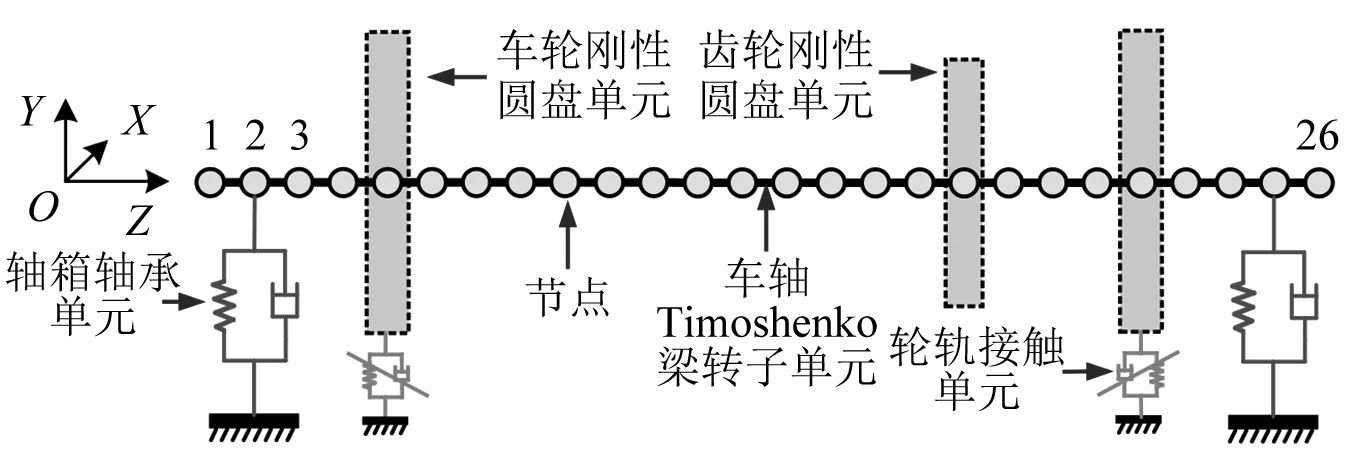
圖2 動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)有限元模型Fig.2 Finite element model of power wheelset rotor system

將各單元矩陣組裝成整體矩陣,可得動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)的動(dòng)力學(xué)微分方程為

(1)

式中,M,C,K,G和F分別為系統(tǒng)的整體質(zhì)量矩陣、阻尼矩陣、剛度矩陣、單位轉(zhuǎn)速下的陀螺矩陣以及外力列向量。其中M,G矩陣主要由模擬車軸的梁轉(zhuǎn)子單元以及模擬車輪和齒輪的剛性圓盤(pán)單元貢獻(xiàn);K矩陣則除了由車軸貢獻(xiàn)外,還包括輪軌接觸約束和軸箱軸承約束的彈性貢獻(xiàn);Ω為輪對(duì)轉(zhuǎn)速。考慮到本文僅研究動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)的彎扭軸模態(tài)特征,故直接令外力向量F=0,且忽略阻尼矩陣C,則可得如下自由振動(dòng)狀態(tài)空間方程

(2)

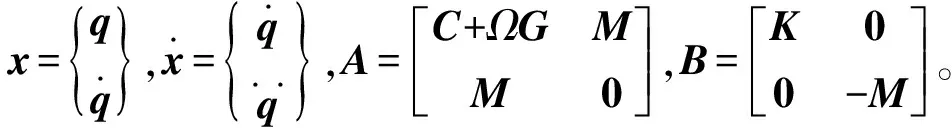
1.2 基于等效圓錐踏面的線性化輪軌接觸單元

輪軌接觸彈性是影響輪對(duì)轉(zhuǎn)子系統(tǒng)振動(dòng)特性的關(guān)鍵因素。為了方便推導(dǎo)線性化的輪軌接觸單元矩陣,這里對(duì)輪軌接觸關(guān)系作一定的簡(jiǎn)化處理:①車輪踏面被等效為錐角為2α的錐面;②忽略車輪和鋼軌的本體彈性以及輪軌切線接觸彈性,僅考慮輪軌法向接觸彈性;③鋼軌接觸表面為連續(xù)外凸曲面,與車輪等效錐面始終保持單點(diǎn)接觸。按照赫茲非線性彈性接觸理論,輪軌法向作用力可表達(dá)為

(3)

式中:G為輪軌接觸常數(shù);δ(t)為輪軌法向接觸壓縮量。顯然,輪軌接觸法向作用力是一個(gè)非線性函數(shù)。為了研究輪對(duì)轉(zhuǎn)子系統(tǒng)的模態(tài)特性,將非線性輪軌法向力線性化,可獲得線性化的輪軌法向接觸剛度

(4)

特別地,如圖3(a)所示,在任意軸重載荷W作用下,輪軌接觸點(diǎn)B將產(chǎn)生法向作用力Fn,若假設(shè)相應(yīng)的輪軌法向接觸壓縮量為δ0,即δ(t) =δ0,那么由式(3)和式(4)即可得車輛軸重平衡狀態(tài)下的輪軌法向作用力和線性化接觸剛度分別為

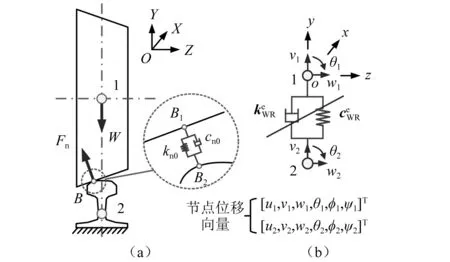
圖3 車輪軸向位移下的力學(xué)分析Fig.3 Mechanical analysis of wheel under axial displacement

(5)

(6)

顯然,該平衡狀態(tài)下的輪軌接觸彈性可由圖3(a)中接觸點(diǎn)B1和B2間的線性化彈簧阻尼元件(kn0,cn0)表達(dá)。但受到接觸位置和方位的影響,該等效線性化元件無(wú)法直接集成到輪對(duì)轉(zhuǎn)子系統(tǒng)方程。

1.2.1 右輪軌接觸單元

為了將上述輪軌法向接觸彈性引入輪對(duì)轉(zhuǎn)子系統(tǒng)有限元方程,這里以右側(cè)輪軌接觸為分析對(duì)象,定義如圖3(b)所示的右輪軌接觸單元。其中,節(jié)點(diǎn)1位于車輪滾動(dòng)圓中心,具有六個(gè)自由度并定義節(jié)點(diǎn)位移向量δ1=[u1,v1,w1,θ1,φ1,ψ1]T;節(jié)點(diǎn)2位于鋼軌截面質(zhì)心,同樣具有六個(gè)自由度且位移向量為δ2=[u2,v2,w2,θ2,φ2,ψ2]T,但由于本文假設(shè)鋼軌底面固結(jié)且不考慮鋼軌本體彈性,因此節(jié)點(diǎn)2等效于接地,自由度為0。相應(yīng)地,該輪軌接觸單元?jiǎng)偠染仃囀且粋€(gè)6×6矩陣,經(jīng)推導(dǎo),單元矩陣形式為

(7)

可以看到單元矩陣中僅在車輪沿y軸沉浮(v)、沿z軸橫移(w)和繞x軸側(cè)滾(θ)三個(gè)自由度上存在元素,這是由于該單元僅考慮了輪軌法向接觸彈性,而該彈性僅在平面oyz內(nèi)提供剛度貢獻(xiàn)。下面分別利用剛度影響系數(shù)法和能量法推導(dǎo)該右輪軌接觸單元矩陣。

1.2.2 基于剛度影響系數(shù)法的單元?jiǎng)偠染仃囉?jì)算

按照剛度影響系數(shù)法,若使剛體車輪在第j個(gè)自由度上產(chǎn)生單位位移而相應(yīng)在車輪第i個(gè)自由度上所施加的力或力矩即為輪軌接觸單元矩陣的元素kij。為此,如圖4所示,在局部坐標(biāo)系oxyz下,令車輪沿z向橫移自由度發(fā)生單位位移w=1,那么由于剛性鋼軌約束限制,車輪受到的附加輪軌接觸法向反力為

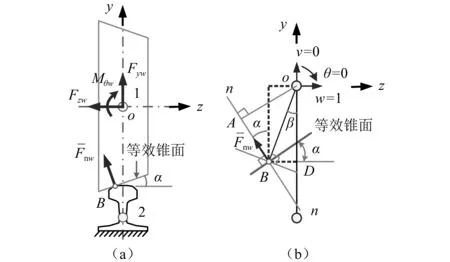
圖4 基于剛度影響系數(shù)法的右輪軌受力分析Fig.4 Force analysis of right wheel-rail based on stiffness influence coefficient method

(8)

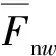
(9)

式中,lOA為局部坐標(biāo)系原點(diǎn)到接觸點(diǎn)法線的距離,大小表達(dá)為

lOA=lOBsin(α+β)

(10)

式中,lOB為原點(diǎn)到接觸點(diǎn)B的距離;β為OB與y軸的夾角。

同理,使車輪沿y軸和繞x軸分別產(chǎn)生垂向和側(cè)滾方向上的單位位移,即v= 1和θ= 1,同樣會(huì)在接觸點(diǎn)B引起附加輪軌接觸法向反力,即

(11)

(12)

顯然,由于單位位移v=1和θ=1是減少輪軌接觸法線壓縮程度的,所以產(chǎn)生的附加反力與w=1時(shí)存在一個(gè)負(fù)號(hào)差異。相應(yīng)地,可得右輪軌接觸單元的其余元素

kvv=-Fyv=-Fnvsin(π/2+α)=kncos2α,
kwv=-Fzv=-Fnvcos(π/2+α)=-knsinαcosα,
kθv=-Mxv=-FnvlOA=knlOAcosα

(13)

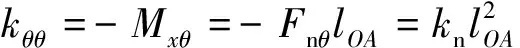
(14)

此外,若令沿x軸伸縮(u)、繞y軸搖頭(φ)和繞z軸點(diǎn)頭(ψ)三個(gè)自由度分別產(chǎn)生單位位移,即u=1,φ=1和ψ=1,可以看到:由于僅考慮輪軌單點(diǎn)接觸的法向彈性,使得這三個(gè)方向上的位移并不產(chǎn)生附加的輪軌法向作用力,故而這三個(gè)自由度所對(duì)應(yīng)的矩陣元素全為零。

綜上,用前述計(jì)算的表達(dá)式重寫(xiě)右輪軌單元矩陣,同時(shí)為簡(jiǎn)化書(shū)寫(xiě)僅保留含非零元素的列與行,有

(15)

1.2.3 基于能量法的單元?jiǎng)偠染仃囉?jì)算

若利用能量法推導(dǎo)輪軌接觸單元?jiǎng)偠染仃?則需首先表達(dá)出單元?jiǎng)菽?進(jìn)而代入拉格朗日方程實(shí)現(xiàn)單元?jiǎng)偠染仃嚨耐茖?dǎo)。如圖3(a)所示,輪軌法向接觸特性被等效線性化為一個(gè)彈簧阻尼元件,因此可按彈簧原理表達(dá)單元?jiǎng)菽?即

(16)

式中,δn為輪軌相對(duì)運(yùn)動(dòng)在接觸點(diǎn)B處引起的法向壓縮量,可由車輪側(cè)接觸點(diǎn)B1和鋼軌側(cè)接觸點(diǎn)B2的相對(duì)位移在法線上的投影計(jì)算得到。考慮到本文假設(shè)鋼軌底面固結(jié)且不考慮其本體彈性,于是依據(jù)剛體上任意一點(diǎn)的位移關(guān)系,利用單元節(jié)點(diǎn)1的位移表達(dá)出接觸點(diǎn)B1的位移

(17)

式中,參數(shù)b和c分別為接觸點(diǎn)B距離單元坐標(biāo)系y軸和z軸的距離。進(jìn)一步將位移分解到法線方向,可得由單元節(jié)點(diǎn)位移δ1=[u1,v1,w1,θ1,φ1,ψ1]T引起的輪軌接觸方向壓縮量

δn=wB1sinα-vB1cosα=

(w1-bθ1)sinα-(v1+cθ1)cosα=Tδ1

(18)

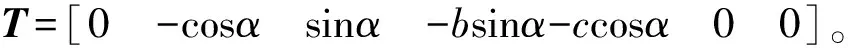
將式(18)代入式(16)獲得由單元節(jié)點(diǎn)位移表達(dá)的勢(shì)能,進(jìn)一步按照拉格朗日方程可得到單元?jiǎng)偠染仃?/p>

(19)

結(jié)果表明式(19)的矩陣運(yùn)算結(jié)果與式(15)相同,即所采用的剛度影響系數(shù)法和能量法的推導(dǎo)結(jié)果一致。

1.2.4 左輪軌接觸單元矩陣

左輪軌接觸單元矩陣可采用前述同樣方法推導(dǎo),如圖5所示。不過(guò),觀察發(fā)現(xiàn):左右輪軌在結(jié)構(gòu)上存在鏡像關(guān)系,即角度α和β在左、右兩輪中的方位恰好是相反的,因此只需將右輪軌接觸單元計(jì)算公式中的α和β分別用-α和-β替換即可得左輪軌接觸單元矩陣,于是

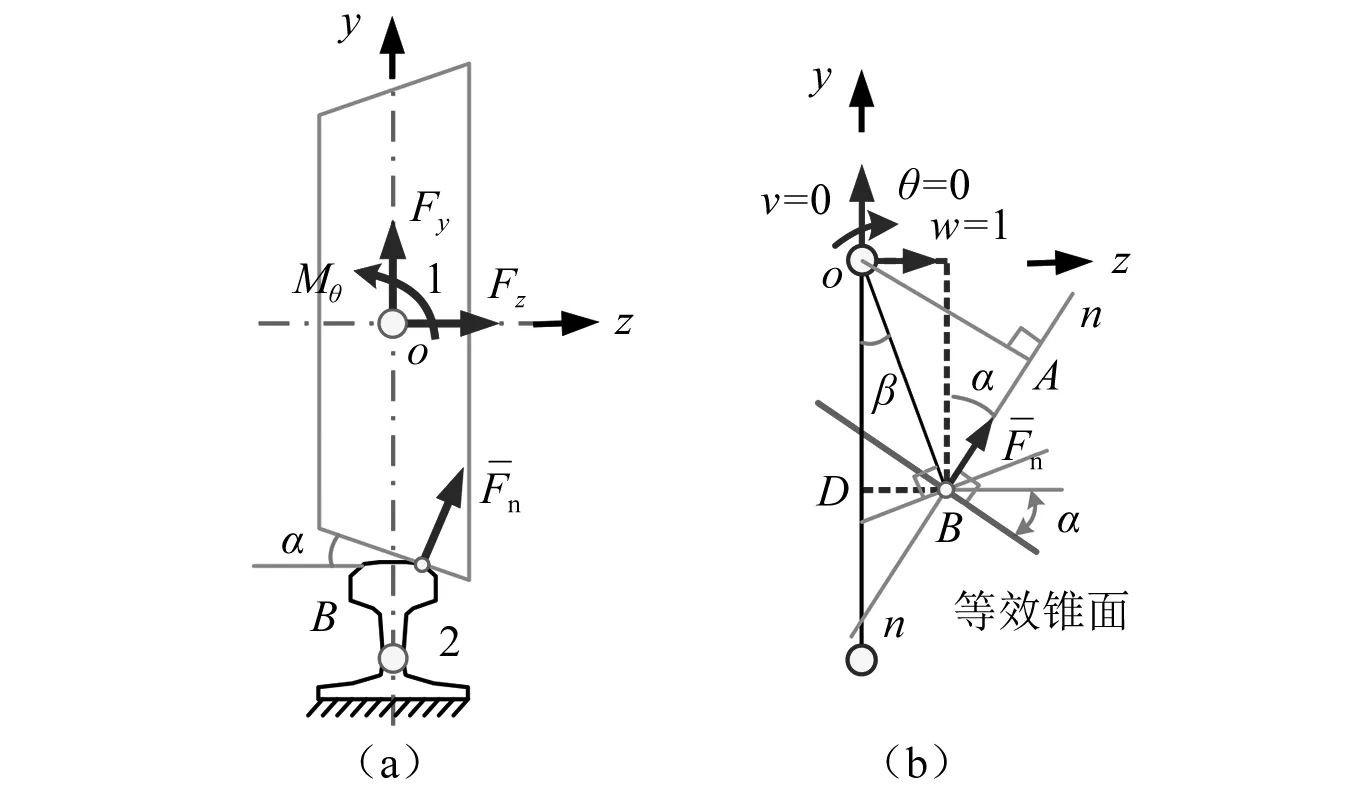
圖5 基于剛度影響系數(shù)法的左輪軌受力分析Fig.5 Force analysis of left wheel-rail based on stiffness influence coefficient method

(20)

需要指出的是,雖然前述線性化輪軌接觸單元是在等效圓錐車輪踏面基礎(chǔ)上推導(dǎo)的,但單元矩陣表達(dá)式同樣適用于車輪真實(shí)踏面,應(yīng)用時(shí)僅需利用諸如跡線法等將輪軌接觸點(diǎn)B的實(shí)際位置確定,并提取接觸點(diǎn)的位置信息(如lOB或lBD)和輪軌接觸角代入單元矩陣表達(dá)式,即可獲得對(duì)應(yīng)狀態(tài)下的線性化輪軌接觸單元矩陣。

2 模型求解與結(jié)果驗(yàn)證

以某型高速動(dòng)車組列車的動(dòng)力輪對(duì)為研究對(duì)象,按照前述方法建立其梁轉(zhuǎn)子有限元模型。其中車輪質(zhì)量為393 kg,直徑轉(zhuǎn)動(dòng)慣量和極轉(zhuǎn)動(dòng)慣量分別為27.3 kg·m2和53.7 kg·m2;大齒輪質(zhì)量為76 kg,直徑轉(zhuǎn)動(dòng)慣量和極轉(zhuǎn)動(dòng)慣量分別為1.56 kg·m2和3 kg·m2;軸箱軸承剛度為1×108N/m;車軸彈性模量為205.8 GPa,密度為7 850 kg/m3。在估算輪軌接觸單元?jiǎng)偠染仃嚂r(shí),取軸重15 t,車輪半徑0.46 m,等效錐形踏面斜度1 ∶10,輪軌接觸點(diǎn)B與車輪質(zhì)心平面的水平距離lBD=10 mm(見(jiàn)圖5)。考慮到我國(guó)高速列車還有提速的空間,取假設(shè)的車輛行駛速度為400 km/h,換算為動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)轉(zhuǎn)速為Ω=2 298.9 r/min。注:后續(xù)凡未明確轉(zhuǎn)速信息的模態(tài)結(jié)果均是指Ω=2 298.9 r/min時(shí)的計(jì)算結(jié)果。

在前述已知的模型數(shù)據(jù)基礎(chǔ)上,利用自編的動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)MATLAB有限元程序,計(jì)算轉(zhuǎn)子的坎貝爾圖、模態(tài)振型以及前4階臨界轉(zhuǎn)速。同時(shí),為了驗(yàn)證結(jié)果正確性,借助ANSYS轉(zhuǎn)子動(dòng)力學(xué)功能模塊,添加自定義的輪軌接觸單元,建立等價(jià)的動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)ANSYS有限元模型,計(jì)算模態(tài)結(jié)果。兩種模型結(jié)果如圖6、圖7和表1所示。注: B1和F1分別為第1階反渦動(dòng)和正渦動(dòng)彎曲振型;T1和A1分別為第1階扭轉(zhuǎn)振型和軸向振型。

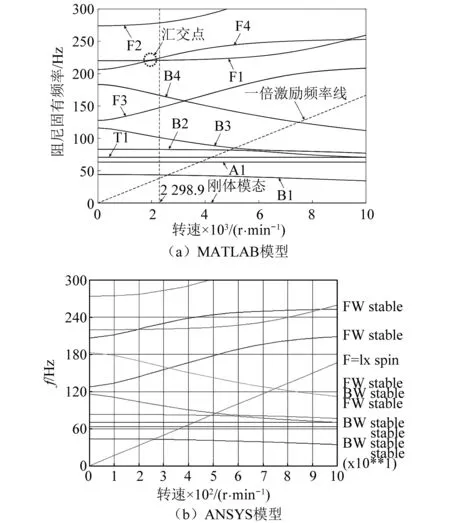
圖6 兩種模型的坎貝爾圖對(duì)比Fig.6 Comparison of Campbell diagram between two models

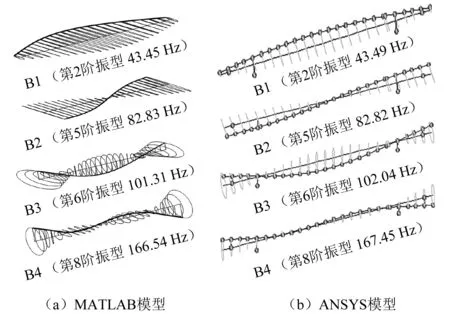
圖7 兩種模型的模態(tài)信息對(duì)比Fig.7 Comparison of modal information between two models

從圖6、圖7和表1可以看出,MATLAB模型得到的坎貝爾圖及其前4階彎曲模態(tài)(振型和固有頻率)和ANSYS模型吻合度較好,且前4階臨界轉(zhuǎn)速也相符合,最大誤差僅0.139 %。因此,驗(yàn)證了所編制的動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)MATLAB有限元程序的正確性。

3 彎扭軸模型下模態(tài)結(jié)果分析

為了更詳細(xì)地分析0～300 Hz內(nèi)動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)的彎扭軸模態(tài)變化規(guī)律,這里進(jìn)一步設(shè)計(jì)四種不同自由度的模態(tài)模型,即四自由度的彎曲模型(模型1)、五自由度的彎扭模型(模型2)、五自由度的彎軸模型(模型3)以及六自由度的彎扭軸模型(模型4,亦即全自由度模型)。考慮到模型4結(jié)果的完備性和篇幅限制,這里僅列出模型4在400 km/h下的模態(tài)數(shù)據(jù)且模態(tài)階數(shù)亦按該數(shù)據(jù)編號(hào),如表2所示。

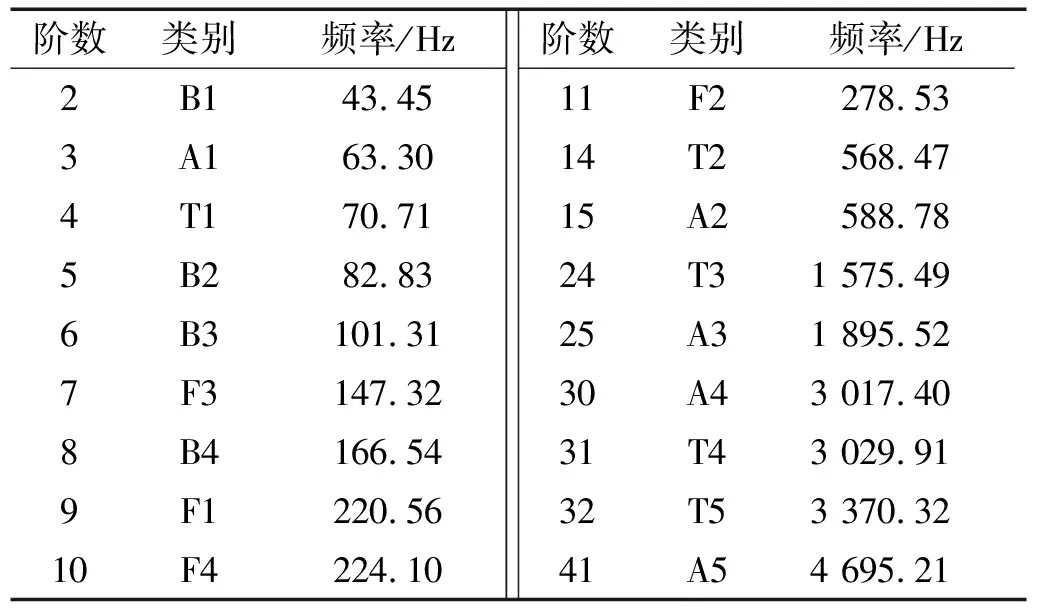
表2 400 km/m下的模態(tài)數(shù)據(jù)(模型4)

同時(shí),將模型1、模型2和模型3分別得到的坎貝爾圖繪制在圖8,結(jié)合模型4的坎貝爾圖(見(jiàn)圖6),可以發(fā)現(xiàn):相比僅具有彎曲自由度的彎曲模型1,彎扭模型2的坎貝爾圖在所關(guān)注的0-300 Hz頻率范圍內(nèi)新增了一根70.71 Hz的扭轉(zhuǎn)振動(dòng)模態(tài)頻率線,而彎軸模型3的坎貝爾圖則是新增了一根63.3 Hz的軸向振動(dòng)模態(tài)頻率線,其余模態(tài)頻率線則是三種模型所共有的彎曲振動(dòng)模態(tài)。進(jìn)一步,對(duì)比圖8與圖6,可以看到具有全自由度的模型4的頻率線涵蓋了前三種模型出現(xiàn)的所有頻率線,即包含了全部的彎曲、扭轉(zhuǎn)和軸向模態(tài)信息,并且具有的固有頻率和振型數(shù)據(jù)也基本保持一致。因此,后續(xù)的模態(tài)分析均以彎扭軸(模型4)的結(jié)果展開(kāi)討論。

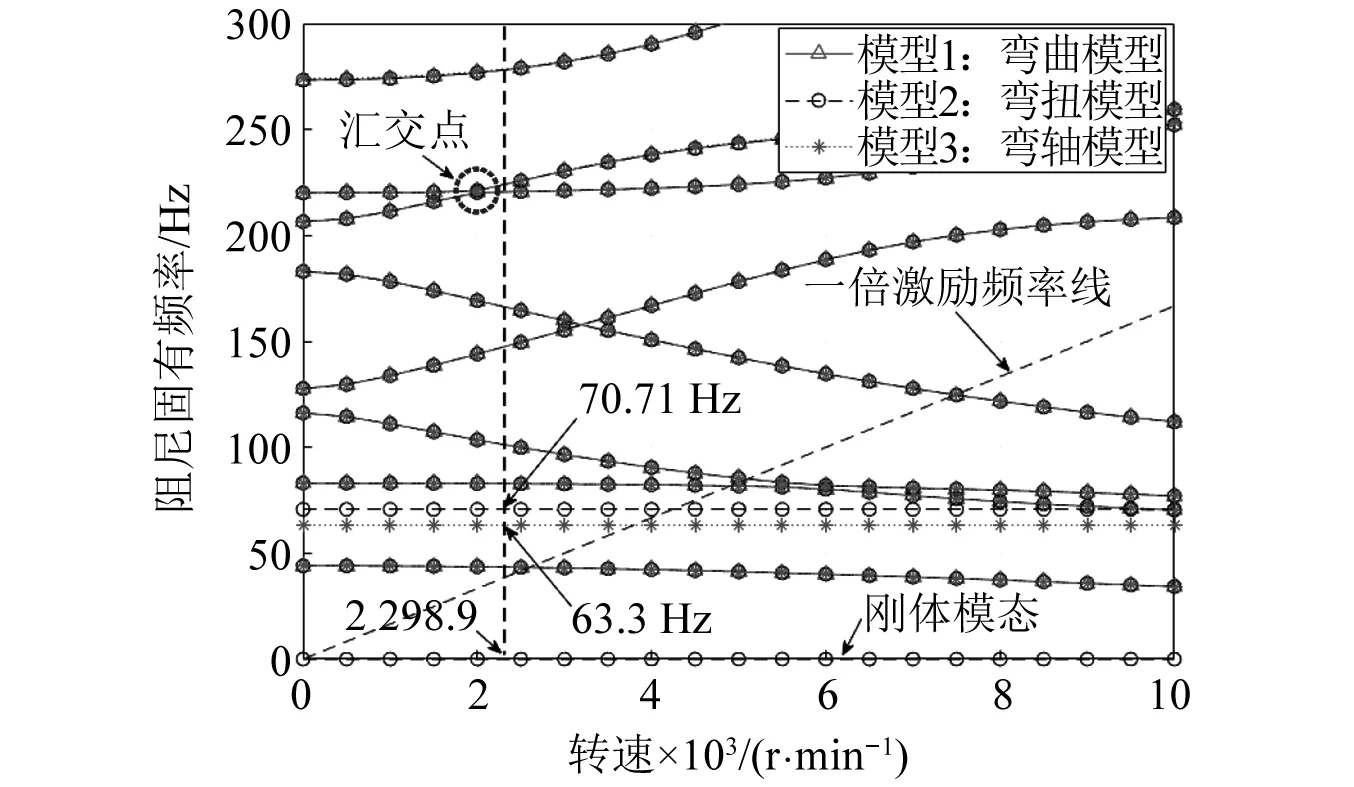
圖8 三種自由度模型坎貝爾圖對(duì)比Fig.8 Campbell diagram comparison of three degree of freedom models

3.1 彎曲模態(tài)的渦動(dòng)軌跡及振型分析

首先,分析動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)彎曲模態(tài)的渦動(dòng)軌跡。圖9繪制了左輪(節(jié)點(diǎn)5)、右輪(節(jié)點(diǎn)22)和大齒輪(節(jié)點(diǎn)18)位置處的前4階彎曲振型渦動(dòng)軌跡。結(jié)合圖7和圖9可以看到,動(dòng)力輪對(duì)轉(zhuǎn)子的彎曲振型均呈現(xiàn)橢圓狀,而且前2階彎曲振型(B1和B2)還整體表現(xiàn)出了嚴(yán)重的“扁平”狀(即橢圓長(zhǎng)半軸顯著大于短半軸)。究其原因主要是由于輪軌接觸約束彈性的存在造成動(dòng)力輪對(duì)轉(zhuǎn)子在垂向(y向)的支承剛度遠(yuǎn)大于縱向(x向)支承剛度,形成了顯著各項(xiàng)異性的支承特性,而且由于左右車輪所在節(jié)點(diǎn)位置較大地參與了第1和第2階彎曲振型(B1和B2),從而使得前2階彎曲振型的渦動(dòng)軌跡呈現(xiàn)嚴(yán)重“扁平”狀。相比起來(lái),左右車輪位置距離第3和第4階彎曲振型(B3和B4)的振節(jié)較近(見(jiàn)圖7),使得輪軌接觸剛度引起的支承剛度各項(xiàng)異性影響變?nèi)?相應(yīng)的渦動(dòng)軌跡扁平化現(xiàn)象也相應(yīng)地變?nèi)酢＝Y(jié)合圖7和圖9可以發(fā)現(xiàn),當(dāng)外界激勵(lì)頻率能夠激發(fā)B1和B2兩階彎曲振型時(shí),動(dòng)力輪對(duì)勢(shì)必將產(chǎn)生較大的縱向主振動(dòng),易出現(xiàn)車輪打滑現(xiàn)象,致使踏面磨損嚴(yán)重;而B(niǎo)3和B4振型激發(fā)下,雖然車輪處振動(dòng)較小,但兩端的軸箱軸承位置振動(dòng)垂向較大,易傳遞給車體而引起車體垂向的劇烈振動(dòng)。

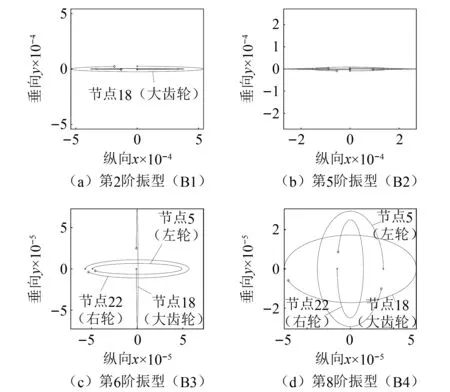
圖9 模型4下前4階彎曲振型渦動(dòng)軌跡Fig.9 The swirling trajectory of the first four bending modes under model 4

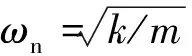
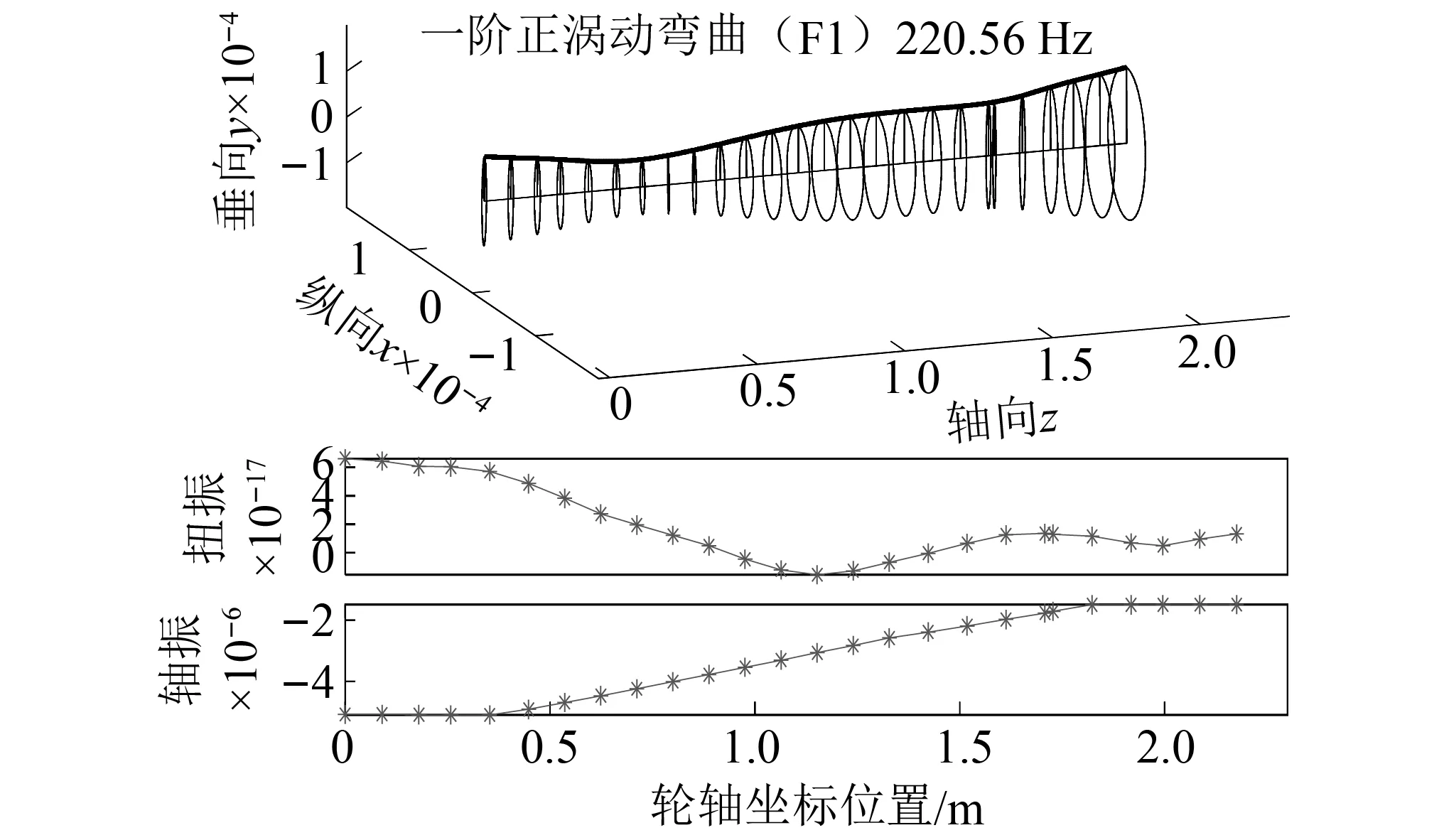
圖10 模型4第9階振型(F1)Fig.10 The 9th mode shape of model 4 (F1)

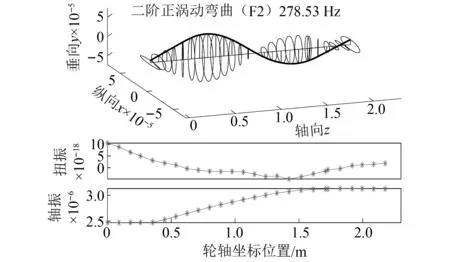
圖11 模型4第11階振型(F2)Fig.11 The 11th mode shape of model 4 (F2)

此外,觀察圖10和圖11中F1和F2彎曲振型包含的扭轉(zhuǎn)和軸向振動(dòng)情況,可以發(fā)現(xiàn)軸向振動(dòng)(量級(jí)在10-6)明顯大于扭轉(zhuǎn)振動(dòng)(量級(jí)在10-17或10-18),更接近彎曲振動(dòng)(量級(jí)10-5),這一現(xiàn)象同樣出現(xiàn)在其他階振型中,表明實(shí)際中彎軸振動(dòng)耦合將會(huì)明顯高于彎扭振動(dòng)耦合。這一現(xiàn)象可以解釋為:因?yàn)檩嗆壗佑|存在一定傾角,使得輪軌接觸垂向和軸向剛度存在較大耦合關(guān)系,當(dāng)車輪受到垂向力的作用下,通過(guò)接觸傾角產(chǎn)生軸向的分力,進(jìn)而引起軸向的振動(dòng),因此,軸向和彎曲振型的同時(shí)出現(xiàn)符合實(shí)際情況,而扭振則難以伴隨彎曲、軸向振動(dòng)一起出現(xiàn)。此外,不難推斷出,由于輪軌接觸剛度的垂向和軸向耦合關(guān)系,使得振型的彎軸振動(dòng)耦合明顯,同時(shí)具有較大的軸向(即對(duì)應(yīng)車體橫向)和垂向振動(dòng),這勢(shì)必將影響車輛的抗傾覆穩(wěn)定性、蛇形穩(wěn)定性等性能評(píng)估。

3.2 模態(tài)頻率線匯交處的振型分析

從圖6可以看到,當(dāng)動(dòng)力輪對(duì)轉(zhuǎn)子轉(zhuǎn)速處在2 000 r/min附近時(shí),模型4的第9階振型和第10階振型對(duì)應(yīng)的頻率線發(fā)生交匯,這種情況同樣存在于模型1～3(見(jiàn)圖8)中。由于該位置所處的車輛實(shí)際行駛速度與當(dāng)前我國(guó)350 km/h十分接近,即接近列車實(shí)際的復(fù)雜高頻運(yùn)行環(huán)境,因此有必要對(duì)交匯位置附近的輪對(duì)轉(zhuǎn)子振型作深入分析。

圖12展示了模型4中轉(zhuǎn)速在2 000 r/min附近動(dòng)力輪對(duì)轉(zhuǎn)子的第9、第10階振型演變情況。理論上講,兩者應(yīng)在頻率交叉點(diǎn)處發(fā)生振型交換,但從圖12中可以看到,隨著轉(zhuǎn)子轉(zhuǎn)速的提升,在1 881～1 991 r/min內(nèi),原本處于第10階的1階正渦動(dòng)彎曲(F1)消失,使得4階正渦動(dòng)彎曲振型(F4)同時(shí)存在于第9、10階振型。此時(shí),1階彎曲振型僅剩1階反渦動(dòng)彎曲振型(B1)存在于第2階,而4階彎曲則由于交匯的影響同時(shí)出現(xiàn)在3階振型中(即第8階的四階反渦動(dòng)彎曲振型和第9、第10階的4階正渦動(dòng)振型)。由于消失的1階正渦動(dòng)彎曲共振主要表現(xiàn)在垂向上(見(jiàn)圖12(b)),易加劇車輛垂向振動(dòng),而加倍出現(xiàn)4階正渦動(dòng)彎曲共振在兩車輪處主要表現(xiàn)在縱向渦動(dòng),使得車輪更易磨損。因此,可以預(yù)測(cè)在該交匯頻率范圍內(nèi)若存在高頻激勵(lì)激發(fā)相應(yīng)共振,則車輪踏面損傷的可能性將會(huì)顯著增加。

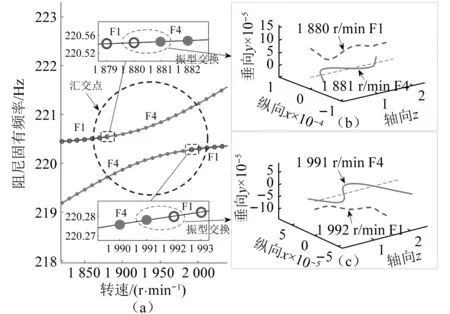
圖12 頻率匯交處振型變化情況Fig.12 The change of vibration mode at frequency intersection

3.3 扭轉(zhuǎn)和軸向模態(tài)的振型分析

作為傳遞驅(qū)動(dòng)力矩和確保列車沿鋼軌走行的關(guān)鍵部件,動(dòng)力輪對(duì)轉(zhuǎn)子的扭轉(zhuǎn)和軸向振動(dòng)模態(tài)對(duì)高速列車動(dòng)力學(xué)性能同樣存在著重要影響,應(yīng)避免正常工況下可能存在的共振問(wèn)題。圖13和圖14分別繪制了模型4的扭轉(zhuǎn)振型以及軸向振動(dòng)振型,結(jié)合圖6和表2可以發(fā)現(xiàn):該動(dòng)力輪對(duì)轉(zhuǎn)子的軸向振型和扭轉(zhuǎn)振型出現(xiàn)的階次非常接近,基本上是在一前一后兩個(gè)相鄰的振型,例如T1(70.71 Hz)在A1(63.3 Hz)之后的1階振型出現(xiàn),A2(588.78 Hz)在T2(568.47 Hz)之后出現(xiàn),但到T5(第32階振型,3 370.32 Hz)和A5(第41階振型,4 695.21 Hz)時(shí)不再出現(xiàn)這種情況。

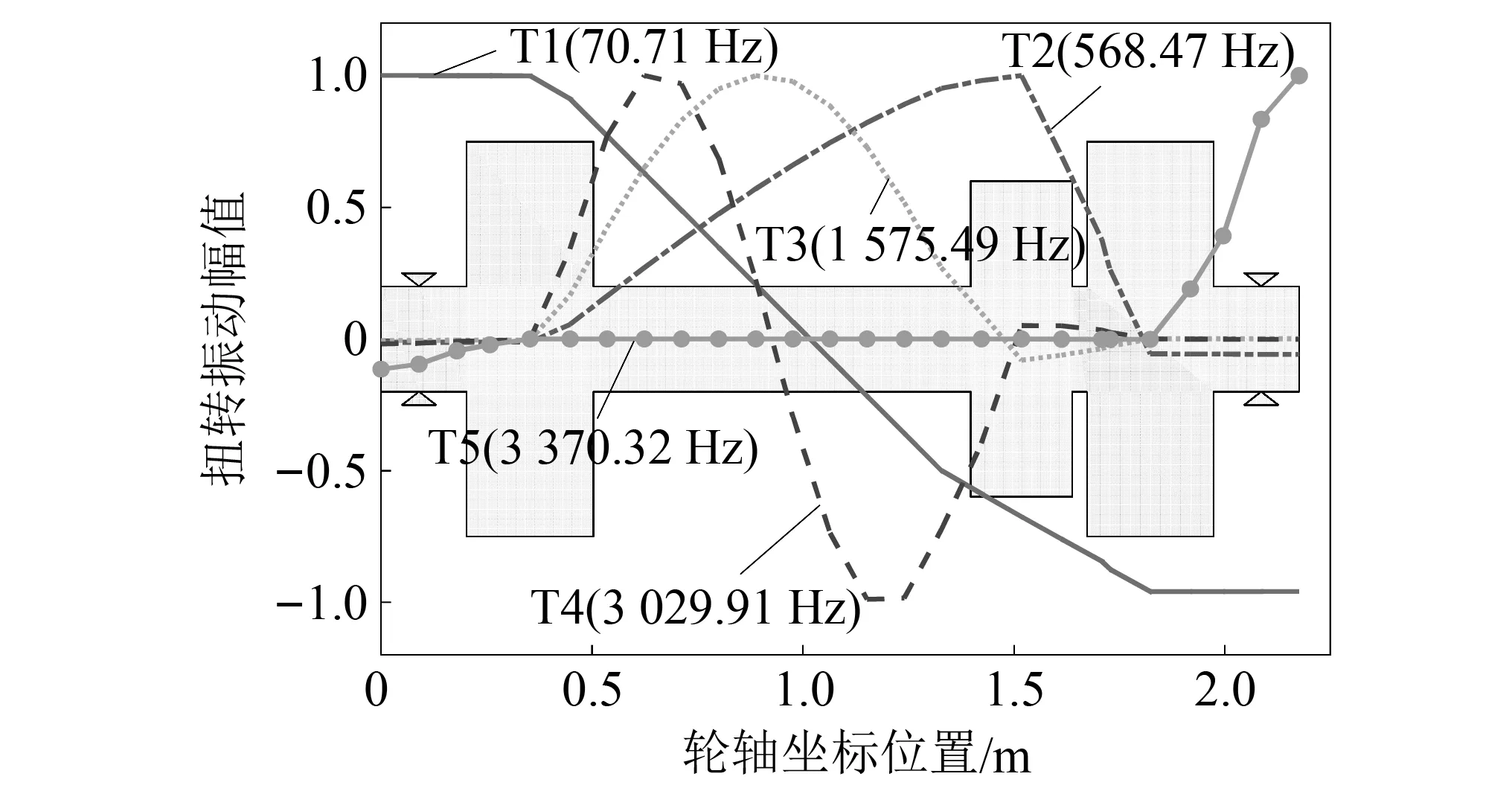
圖13 模型4的扭轉(zhuǎn)振型Fig.13 Torsional mode shapes of model 4

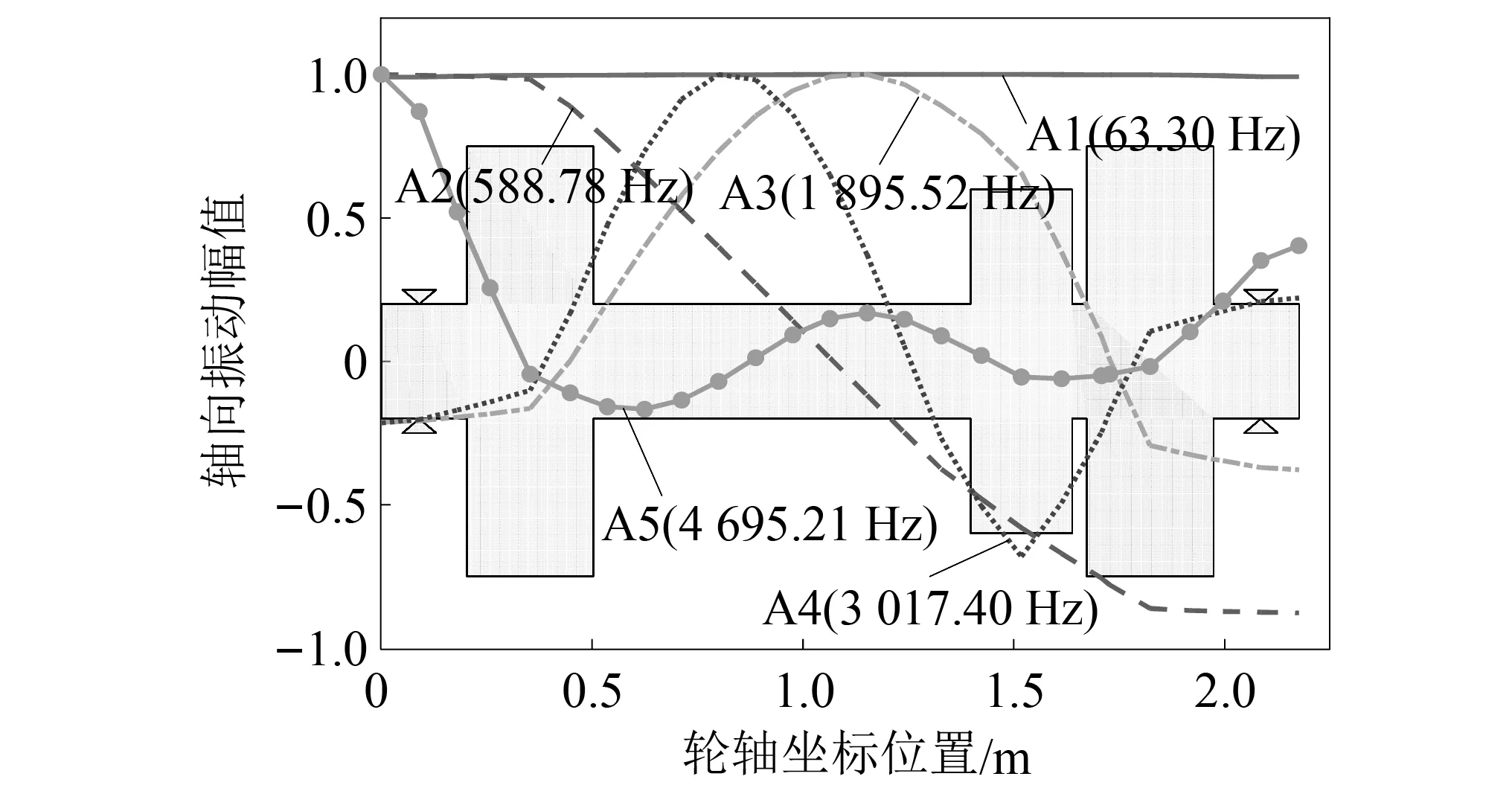
圖14 模型4的軸向振型Fig.14 Axial mode shapes of model 4

由扭轉(zhuǎn)振型圖13可知,T1在左右車輪兩側(cè)的振型較大,車軸中間部位的振型最小,在經(jīng)過(guò)左右車輪節(jié)點(diǎn)位置以及大齒輪節(jié)點(diǎn)位置時(shí),均出現(xiàn)振型幅值突變的情況(幅值減小或增幅減緩)。扭轉(zhuǎn)振幅突變同樣出現(xiàn)在T2,T3,T4及T5,這表明扭振的傳遞會(huì)被具有較大轉(zhuǎn)動(dòng)慣量的元件(如車輪、大齒輪等)所阻礙,甚至阻斷[18]。其中,T2在大齒輪節(jié)點(diǎn)處出現(xiàn)最大振幅,而在車輪兩側(cè)振幅相對(duì)小的多,若該振型被激發(fā)則極易引起齒輪嚙合不平穩(wěn);T3和T4的振動(dòng)形態(tài)則主要被限制在左右車輪之間的車軸部位;T5的扭轉(zhuǎn)振動(dòng)主要出現(xiàn)在左右車輪的外伸軸段部分,其中右側(cè)車輪的外伸軸段扭振幅度遠(yuǎn)大于左側(cè),若該振型被激發(fā)則易引起右端軸箱軸承的扭振波動(dòng),加劇內(nèi)、外圈和滾子的接觸疲勞,同時(shí)也易使得車軸在右車輪處發(fā)生扭振疲勞。

由軸向振型圖14可知,在具有大質(zhì)量的車輪和齒輪部位也呈現(xiàn)軸向振動(dòng)幅值突變的現(xiàn)象,但明顯程度略低于扭轉(zhuǎn)振型。其中:A1(63.3 Hz)的振幅波動(dòng)非常小(實(shí)際計(jì)算出的最大振幅(4.89×10-4m)及最小幅值(4.85×10-4m)相差也很小),在無(wú)量綱化振型圖中幾近一條直線,表明該振型是動(dòng)力輪對(duì)轉(zhuǎn)子在軸向約束彈性限制下沿軸向作整體運(yùn)動(dòng)的振型,因此該振型中的動(dòng)力輪對(duì)可看作剛體;A2(588.78 Hz)的最大振幅位于左右兩側(cè)車輪的外側(cè)軸段,整個(gè)車軸呈現(xiàn)向兩側(cè)的對(duì)稱拉壓運(yùn)動(dòng),該振型下易造成車輪輪緣外側(cè)與鋼軌擠壓,進(jìn)而加劇車輪踏面的磨損;A3(1 895.52 Hz)最大振幅位置出現(xiàn)在車軸軸身中心部位;A4(3 017.4 Hz)最大振幅位置出現(xiàn)在軸身中心以及大齒輪等效集中質(zhì)量部位,在大齒輪處達(dá)到最大振幅后出現(xiàn)反轉(zhuǎn),振幅迅速呈下降趨勢(shì),此時(shí)軸向大振幅下引起的擠壓易使斜齒輪嚙合面法向受壓迫,加速齒面磨損;A5(4 695.21 Hz)最大振幅位置出現(xiàn)在車軸靠近左車輪的一端,向右出現(xiàn)振幅不規(guī)律的波動(dòng),整體呈現(xiàn)向右側(cè)的軸向振動(dòng)。

3.4 輪軌接觸點(diǎn)位置對(duì)模態(tài)結(jié)果的影響

考慮到輪軌接觸點(diǎn)B的初始位置會(huì)因車輪橫向運(yùn)動(dòng)或鋼軌軌底坡等原因而發(fā)生變化,如圖15所示。本小節(jié)以點(diǎn)B到車輪質(zhì)心平面的距離lBD為參數(shù)(圖5所示),討論不同lBD值下動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)振動(dòng)模態(tài)的變化規(guī)律。

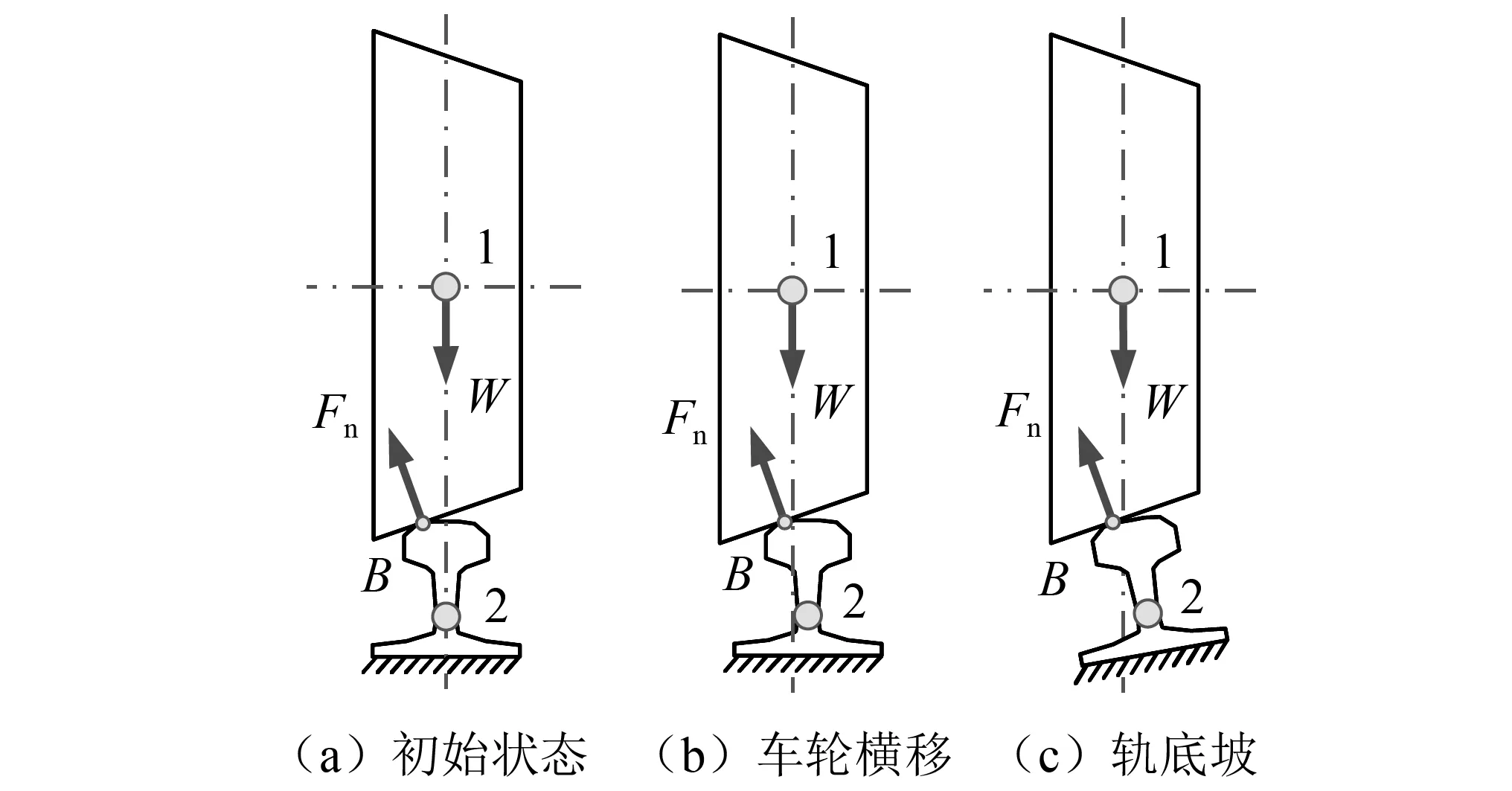
圖15 車輪橫移或軌底坡引起的輪軌接觸位置變化Fig.15 Wheel rail contact position change caused by wheel lateral movement or rail bottom slope

為此,選取lBD∈[0, 0.02]m內(nèi)的不同值計(jì)算系統(tǒng)固有頻率,在統(tǒng)計(jì)前20階固有頻率變化后,發(fā)現(xiàn)隨著lBD值的改變,第2～5、第12及第14～20階模態(tài)的固有頻率變化均在1 Hz以內(nèi),可見(jiàn)較低和較高階模態(tài)固有頻率受輪軌接觸點(diǎn)位置的改變影響非常有限。相比之下,中間模態(tài)(即第6～11及第13階)的固有頻率則受輪軌接觸點(diǎn)位置的改變影響更大一些,如表3所示。注:變化中“↑”“↓”分別表示固有頻率值上升或下降超過(guò)1 Hz,“↗”“↘”分別表示固有頻率值上升或下降低于1 Hz,“-”表示固有頻率值不變。

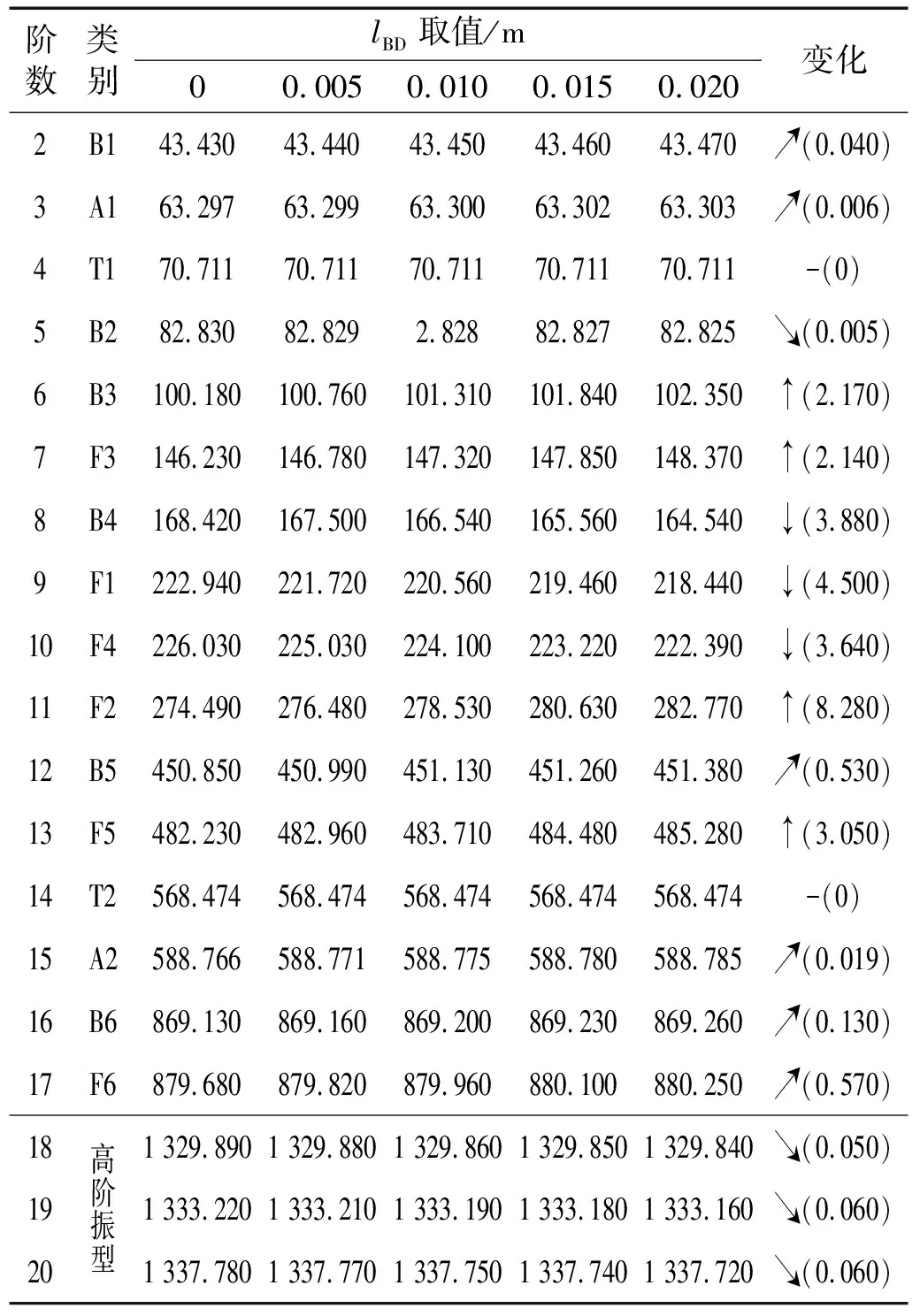
表3 模型4模態(tài)頻率隨lBD值變化情況

由表3可以發(fā)現(xiàn),第6(B3)、第7(F3)、第11(F2)和第13階(F5)模態(tài)的頻率隨著lBD取值增大而增大;第8(B4)、第9(F1)和第10階(F4)模態(tài)的固有頻率隨著lBD取值增大而減小。此外,動(dòng)力輪對(duì)的軸向模態(tài)頻率受lBD的影響較于彎曲模態(tài)小很多,而扭轉(zhuǎn)模態(tài)頻率則完全不受lBD的影響。總體來(lái)說(shuō),動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)固有頻率受輪軌接觸點(diǎn)位置的影響較小(模態(tài)頻率變化最大值僅8.28 Hz)。

4 考慮故障激勵(lì)的動(dòng)力輪對(duì)共振模態(tài)分析

在實(shí)際運(yùn)行中,動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)不斷受到輪軌接觸、軸箱軸承力、齒輪嚙合力、車輪損傷、軌道不平順等外部復(fù)雜激勵(lì)的持續(xù)作用,激勵(lì)頻率不但范圍寬,而且異常豐富,特別是存在故障時(shí)[19-22]。顯然,在復(fù)雜的激勵(lì)頻率下,高速運(yùn)行的柔性動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)極易產(chǎn)生振動(dòng)穩(wěn)定性問(wèn)題,誘發(fā)共振模態(tài)。

按照振動(dòng)穩(wěn)定性設(shè)計(jì)準(zhǔn)則,假設(shè)當(dāng)激勵(lì)頻率處于系統(tǒng)固有頻率的5%以內(nèi)便認(rèn)為系統(tǒng)存在共振問(wèn)題。表4列出了前述幾種典型故障激勵(lì)下本算例中動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)可能被激發(fā)的共振模態(tài)信息。其中,v=400 km/h為列車運(yùn)行速度;R=0.46 m為車輪半徑;f1=93.36 Hz為電機(jī)軸轉(zhuǎn)頻;f2=38.44 Hz為輪軸轉(zhuǎn)頻;fm=3267.6 Hz為齒輪嚙合頻率(大齒輪數(shù)為85,小齒輪數(shù)為35);Z=19為軸承滾子數(shù);d=26 mm為滾動(dòng)體直徑;α=10°為軸承接觸角;dm=183.93 mm為軸承節(jié)徑。

表4 典型外部激勵(lì)下動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)的共振模態(tài)

可以看到,在400 km/h的高速列車運(yùn)行環(huán)境下,這些典型激勵(lì)頻率很容易落入動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)的共振頻率范圍內(nèi),特別是車輪損傷故障頻率。當(dāng)考慮軌道不平順激勵(lì)時(shí),其短波、中波和長(zhǎng)波下的激勵(lì)頻率通過(guò)輪軌接觸作用傳遞到輪對(duì)系統(tǒng),則更易誘發(fā)系統(tǒng)共振。因此,面對(duì)越來(lái)越高速的動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng),在全面掌握其彎曲、扭轉(zhuǎn)和軸向振動(dòng)特性的同時(shí),應(yīng)注重抗共振模態(tài)設(shè)計(jì)。不過(guò),需要特別注意的是,雖然動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)中與齒輪和軸承相關(guān)的故障激勵(lì)頻率存在達(dá)到模態(tài)共振條件的情形,但考慮到與其相關(guān)的故障激勵(lì)誘發(fā)的振動(dòng)能量通常很小,尤其是諸如齒輪裂紋、軸承保持架等振動(dòng)能量極小的故障激勵(lì),往往是無(wú)法誘發(fā)相對(duì)應(yīng)的系統(tǒng)共振模態(tài)的,最多是加劇輪對(duì)系統(tǒng)或零件自身的局部振動(dòng),在抗共振模態(tài)設(shè)計(jì)和制定維護(hù)策略時(shí)應(yīng)與輪軌故障激勵(lì)區(qū)分對(duì)待。

5 結(jié) 論

聚焦現(xiàn)有高速列車動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)振動(dòng)特性的研究不足,在充分考慮輪對(duì)的柔性、陀螺效應(yīng)和約束彈性基礎(chǔ)上,推導(dǎo)了一種基于等效圓錐踏面的線性化輪軌接觸單元,建立了基于鐵木辛柯梁轉(zhuǎn)子有限元理論的動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)方程,詳細(xì)討論了輪軌接觸彈性和軸箱軸承彈性約束下高速列車動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)的彎曲、軸向和扭轉(zhuǎn)振動(dòng)特性。主要研究結(jié)論如下:

(1) 利用剛度影響系數(shù)法和能量法分別推導(dǎo)了輪軌接觸單元,且兩種方法結(jié)果一致;所推導(dǎo)的輪軌接觸單元不但適用于圓錐踏面車輪,還可推廣至具有真實(shí)車輪踏面的場(chǎng)合,僅需根據(jù)實(shí)際情況獲得輪軌接觸點(diǎn)位置和接觸角即可。

(2) 通過(guò)與ANSYS模型結(jié)果作對(duì)比,驗(yàn)證了自編MATLAB模型程序的正確性;基于自編MATLAB程序設(shè)計(jì)的四種模態(tài)模型中具有全自由度的模型4的模態(tài)結(jié)果涵蓋了其他三種自由度模型的所有頻率和振型。

(3) 詳細(xì)分析了全自由度模型4的彎扭軸模態(tài)規(guī)律及其與輪對(duì)宏觀振動(dòng)特性關(guān)系,可以發(fā)現(xiàn)——①受輪軌接觸剛度的影響,一方面使得反渦動(dòng)彎曲模態(tài)(B1和B2)的渦動(dòng)軌跡沿縱向呈現(xiàn)嚴(yán)重的扁平狀,該振型激發(fā)狀態(tài)下易加劇車輪踏面的磨損;另一方面將正渦動(dòng)彎曲模態(tài)(F1和F2)推遲出現(xiàn)在了更高階的頻率段;②由于推導(dǎo)的輪軌接觸單元考慮了垂向和軸向的剛度耦合關(guān)系,使得耦合下的軸向和彎曲振動(dòng)量級(jí)接近(見(jiàn)F1和F2),對(duì)車輛運(yùn)行抗傾覆性、蛇形穩(wěn)定性等性能評(píng)估將產(chǎn)生影響;③具有較大等效轉(zhuǎn)動(dòng)慣量和質(zhì)量的車輪和齒輪零件使得對(duì)應(yīng)車軸位置處的扭轉(zhuǎn)和軸向振動(dòng)顯著減小;④輪軌接觸點(diǎn)位置對(duì)動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)的振動(dòng)特性存在影響,但影響程度較小。

(4) 在典型外部激勵(lì)下動(dòng)力輪對(duì)轉(zhuǎn)子系統(tǒng)存在共振失穩(wěn)的可能性,尤以車輪損傷故障激勵(lì)可能激發(fā)的系統(tǒng)模態(tài)階數(shù)較多,實(shí)際中應(yīng)開(kāi)展合理化模態(tài)設(shè)計(jì)。