滾珠絲杠支承系統(tǒng)滾珠絲杠軸承綜合軸向變形分析計(jì)算

徐曉華 蔣桂平 韓興國(guó) 張政潑

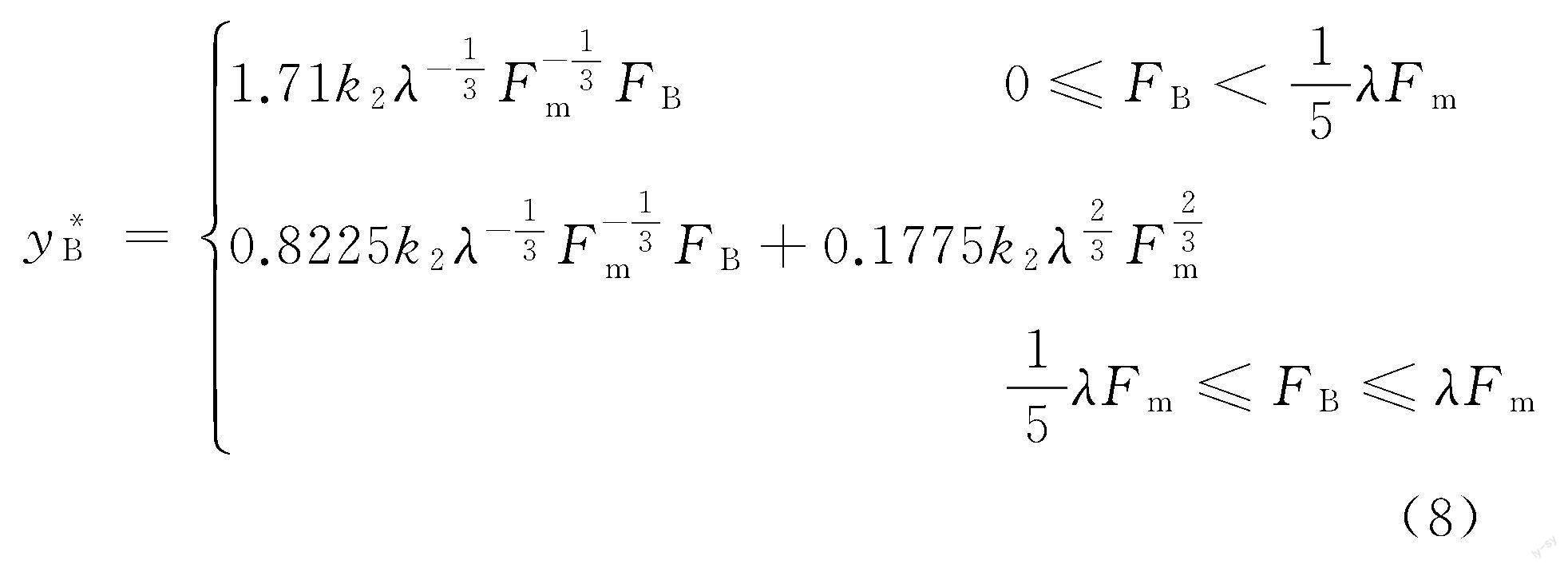
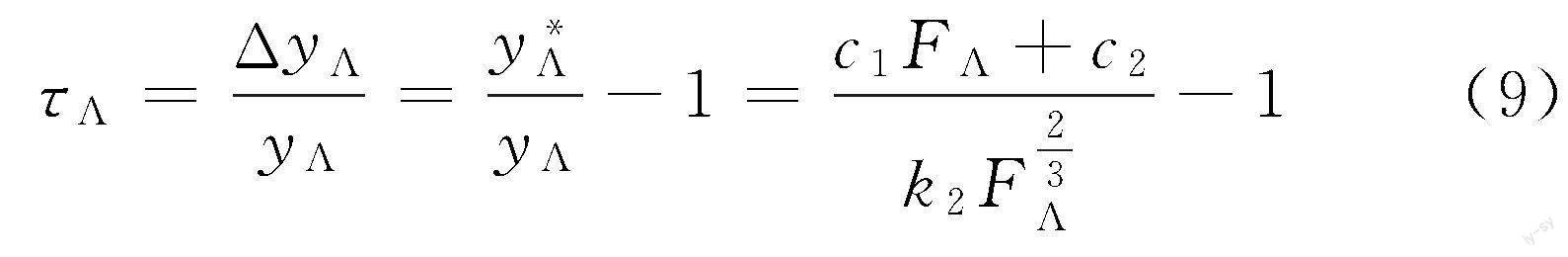
摘要：對(duì)兩種常用滾珠絲杠支承系統(tǒng)的滾珠絲杠軸承進(jìn)行分析，采用三折線逼近法推導(dǎo)出滾珠絲杠支承系統(tǒng)滾珠絲杠軸承綜合軸向變形量隨位置和負(fù)載變化的雙變量函數(shù)關(guān)系式，綜合軸向變形量隨位置的變化形態(tài)近似呈開口向下的非對(duì)稱弧線形，推導(dǎo)出最大綜合軸向變形量及其位置坐標(biāo)的計(jì)算式。分析和試驗(yàn)結(jié)果表明，隨著滾珠絲杠、軸承兩者最大變形量之比逐漸減小，滾珠絲杠軸承綜合軸向變形量變化形態(tài)趨于平緩，出現(xiàn)最大變形量的位置坐標(biāo)逐漸沿負(fù)載方向離開兩支承跨距的中心。

關(guān)鍵詞：滾珠絲杠支承系統(tǒng)；軸向負(fù)載；綜合軸向變形；位置坐標(biāo)

中圖分類號(hào)：TG502.1;TH132

DOI：10.3969/j.issn.1004132X.2023.07.009

Analysis and Calculation of Comprehensive Axial Deformations of

Ball Screw-Bearing in Ball Screw Support Units

XU Xiaohua1 JIANG Guiping2 HAN Xingguo1 ZHANG Zhengpo1

1.College of Mechanical and Electrical Engineering，Guilin University of Aerospace Technology，

Guilin，Guangxi，541004

2.Guilin Guanglu Measuring Instrument Co.，Ltd.，Guilin，Guangxi，541213

Abstract： The ball screw-bearing of two kinds of common ball screw support units were analyzed. Using three-broken-line approximation method， the bivariate function of comprehensive axial deformations of ball screw-bearing in ball screw support units was derived with the change of position and load. The comprehensive axial deformations with the change of position was approximately asymmetric arc with the opening downward， and the calculation formula of maximum comprehensive axial deformations and the position coordinate were derived. Analysis and experimental results show that the change form of the comprehensive axial deformations of ball screw-bearing tends to flat while the ratio of maximum deformation between ball screw and bearing decreasing gradually， and the position coordinates of maximum deformation move away gradually from the center of the two supporting spans along the load direction.

Key words： ball screw support unit; axial load; comprehensive axial deformation; position coordinate

0 引言

滾珠絲杠傳動(dòng)機(jī)構(gòu)是數(shù)控機(jī)床進(jìn)給傳動(dòng)系統(tǒng)的關(guān)鍵部分，在負(fù)載作用下滾珠絲杠支承系統(tǒng)的軸向變形是影響位置精度的主要部分。

滾珠絲杠支承系統(tǒng)在軸向負(fù)載作用下產(chǎn)生的軸向變形量包括絲杠軸向拉壓變形、軸承接觸變形、絲杠螺母接觸變形、絲杠扭轉(zhuǎn)變形、支承座和螺母座的軸向變形等，其中絲杠和軸向承力軸承（以下簡(jiǎn)稱軸承）的軸向變形占總變形的大部分。現(xiàn)行的絲杠系統(tǒng)軸向變形計(jì)算方法主要采用各部分獨(dú)立計(jì)算和直接疊加的方式計(jì)算［1-3］。近年對(duì)滾珠絲杠支承系統(tǒng)相關(guān)的預(yù)拉伸力、軸向變形和精度等進(jìn)行分析的研究較多，如文獻(xiàn)［4-5］考慮最大負(fù)載和溫升作用的滾珠絲杠支承系統(tǒng)預(yù)拉伸力，指出了兩端固定絲杠系統(tǒng)受力和變形復(fù)雜的相互關(guān)聯(lián)性；文獻(xiàn)［6］考慮接觸區(qū)外彈性變形的滾珠絲杠副靜剛度分析，主要研究了一端固定一端浮動(dòng)的支承形式；文獻(xiàn)［7］研究包括聯(lián)軸器環(huán)節(jié)的滾珠絲杠進(jìn)給系統(tǒng)靜剛度模型；文獻(xiàn)［8］對(duì)滾珠絲杠副主要環(huán)節(jié)進(jìn)行計(jì)算，包括對(duì)軸承環(huán)節(jié)的有限元分析；文獻(xiàn)［9］對(duì)兩端雙向固定的包括絲杠軸向剛度和絲杠螺母間軸向剛度兩個(gè)環(huán)節(jié)的滾珠絲杠副軸向靜剛度進(jìn)行建模與研究，但沒有包括軸承環(huán)節(jié)。以上研究主要基于各部分變形獨(dú)立計(jì)算直接疊加的方式。

另外，文獻(xiàn)［10］應(yīng)用有限元法對(duì)兩端雙向固定、一端雙向固定一端浮動(dòng)兩種支承形式的滾珠絲杠軸承系統(tǒng)進(jìn)行軸向剛度的分析研究，通過(guò)圖線形式給出剛度變化特性；文獻(xiàn)［11］研究了絲杠螺母位于不同位置以及不同的軸向載荷時(shí)，滾珠絲杠系統(tǒng)軸向、橫向和扭轉(zhuǎn)等多種變形對(duì)絲杠螺母接觸載荷分布的聯(lián)合影響特性；文獻(xiàn)［12］研究了滾珠絲杠傳動(dòng)系統(tǒng)軸向和角度方向的振動(dòng)變形問(wèn)題；文獻(xiàn)［13］研究了滾珠絲杠傳動(dòng)系統(tǒng)軸向彈性變形模型，并提出了變形補(bǔ)償方式以提高定位精度。以上研究主要針對(duì)一端雙向固定一端浮動(dòng)支承形式。

實(shí)際上，常用的滾珠絲杠支承形式還包括兩端單向固定、一端雙向固定一端單向固定形式，這兩種形式與兩端雙向固定形式需采取預(yù)拉伸安裝措施，此時(shí)預(yù)拉伸力就是軸承的預(yù)緊力。通過(guò)分析可知，在軸向負(fù)載作用下，絲杠軸向拉壓變形、軸承的軸向接觸變形及作用力相互關(guān)聯(lián)和影響，絲杠軸承應(yīng)作為一個(gè)整體進(jìn)行綜合分析。

現(xiàn)有研究都未涉及滾珠絲杠軸承環(huán)節(jié)的綜合軸向變形隨位置坐標(biāo)和軸向負(fù)載變化的函數(shù)解析式，以及出現(xiàn)最大綜合軸向變形時(shí)的絲杠螺母位置坐標(biāo)的計(jì)算確定方法。本文采用整體描述和綜合分析方法，對(duì)滾珠絲杠支承系統(tǒng)滾珠絲杠軸承環(huán)節(jié)的上述分析計(jì)算方法展開研究，主要針對(duì)文獻(xiàn)基本沒有涉及但卻常用的兩端單向固定、一端雙向固定一端單向固定兩種支承形式。

1 絲杠軸承受力與變形分析

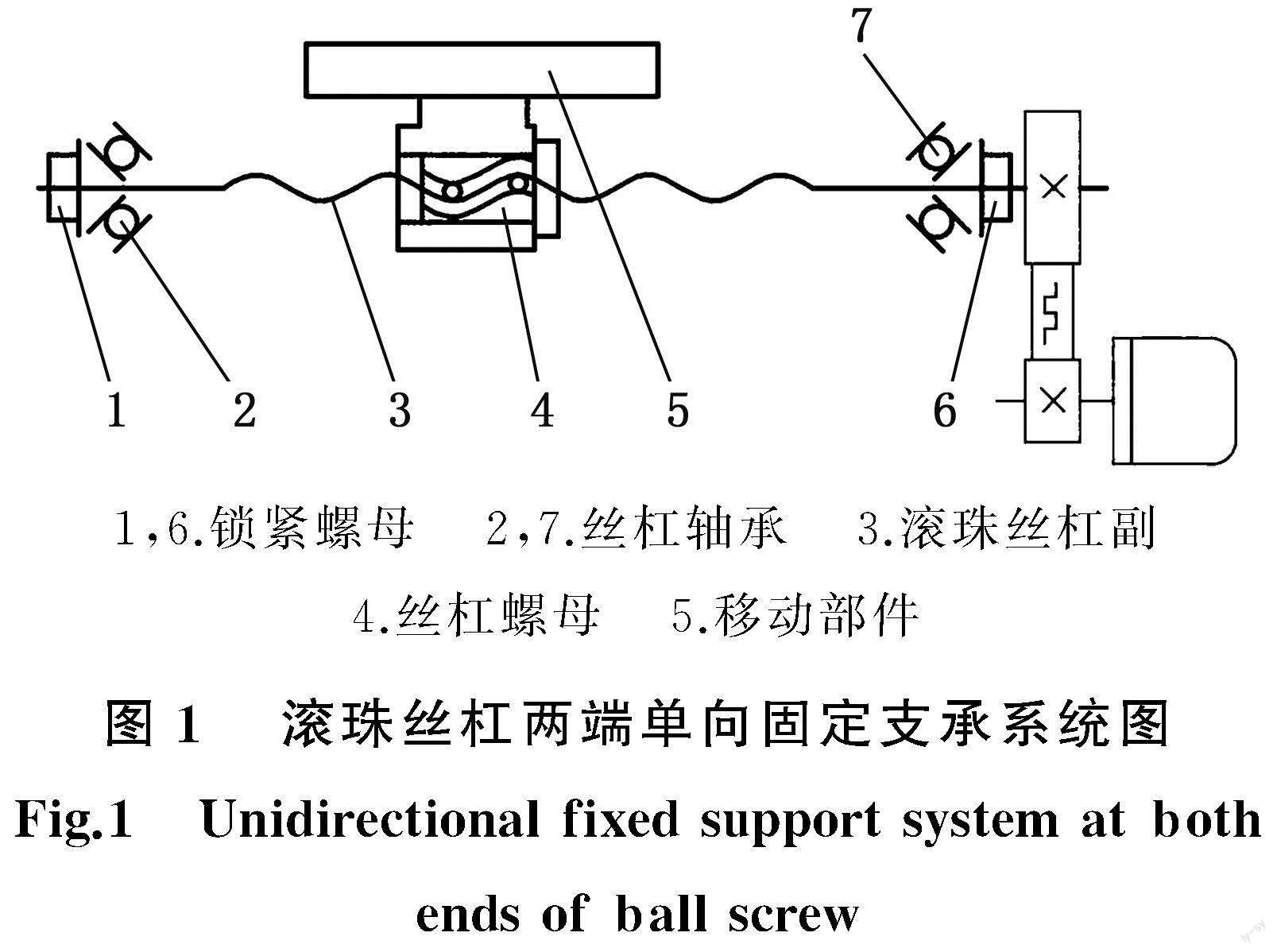
滾珠絲杠旋轉(zhuǎn)類型的支承形式主要有以下五種：一端雙向固定一端自由、一端雙向固定一端支承（浮動(dòng)）、兩端單向固定、一端雙向固定一端單向固定、兩端雙向固定，其中后三種都要采取預(yù)拉伸安裝方式，使得在絲杠支承系統(tǒng)最大軸向負(fù)載和工作溫升情況下，絲杠始終處于受拉狀態(tài)或臨界狀態(tài)。在預(yù)拉伸力作用下，第三、四種絲杠支承系統(tǒng)的絲杠軸承受力和變形特性相同，這是因?yàn)椋谒姆N支承形式負(fù)載指向單向端時(shí)比指向雙向端時(shí)的剛度相對(duì)較弱，且與第三種支承形式相同，而弱方向特性作為代表特性。因此本研究針對(duì)兩端單向固定支承形式開展，結(jié)論也適用于一端雙向固定一端單向固定支承形式。

通常滾珠絲杠支承系統(tǒng)需綜合考慮最大軸向負(fù)載和工作溫升從而確定綜合臨界預(yù)拉伸力，當(dāng)達(dá)到工作溫升，進(jìn)入熱平衡后，綜合臨界預(yù)拉伸力即變?yōu)橹豢紤]最大軸向負(fù)載時(shí)的臨界預(yù)拉伸力［4］，因此筆者分析計(jì)算絲杠支承系統(tǒng)的軸向變形時(shí)，相當(dāng)于只考慮最大軸向負(fù)載時(shí)的狀態(tài)。在下文敘述中，筆者主要提及只考慮最大軸向負(fù)載的臨界預(yù)拉伸力，但實(shí)際施加的是綜合預(yù)拉伸力。

圖1為數(shù)控機(jī)床滾珠絲杠兩端單向固定支承形式示意圖。圖2為絲杠支承系統(tǒng)處于預(yù)拉伸狀態(tài)但還未作用有軸向負(fù)載時(shí)的初始狀態(tài)力學(xué)模型圖。其中，F(xiàn)s0為只考慮最大軸向負(fù)載時(shí)的臨界預(yù)拉伸力（以下簡(jiǎn)稱臨界預(yù)拉伸力），F(xiàn)s0=λFm，λ為臨界預(yù)拉伸力系數(shù)，F(xiàn)m為最大軸向負(fù)載。A、B分別表示左、右軸承，L為支承跨距，C表示絲杠螺母，x為絲杠螺母（以下簡(jiǎn)稱螺母）位置坐標(biāo)。在Fs0作用下，絲杠AC段、BC段拉伸變形分別為Δ0AC、Δ0BC，軸承A、B軸向接觸變形為Δ0A、Δ0B。圖3為軸向負(fù)載Fa作用下的力學(xué)模型圖，Ls為螺母移動(dòng)的極限行程位置，F(xiàn)A、FB分別為軸承A、B的軸向反力，ΔA、ΔB分別為軸承A、B的軸向接觸變形，ΔAC、ΔBC分別為絲杠AC段、BC段軸向拉伸變形，Δx為螺母C由于絲杠和軸承變形而形成的綜合軸向變形量。由于當(dāng)Fa不變時(shí)絲杠螺母間的軸向接觸變形為恒定［14］，為了便于分析，此項(xiàng)變形不納入本文的滾珠絲杠軸承變形部分。

在實(shí)際應(yīng)用中，可能根據(jù)需要采用比臨界預(yù)拉伸力略大的預(yù)拉伸力，但對(duì)分析計(jì)算影響較小，因此本研究只考慮按臨界預(yù)拉伸力安裝的場(chǎng)合。

根據(jù)圖3狀態(tài)的受力平衡，有

FA=FB+Fa（1）

根據(jù)圖2、圖3的變形狀態(tài)，有如下變形量平衡方程

Δx=（ΔAC－Δ0AC）+（ΔA－Δ0A）=（Δ0BC－ΔBC）+（Δ0B－ΔB）（2）

在力F作用下，絲杠軸向拉壓變形為［15］Δ=k1xF，式中k1為絲杠的變形因數(shù)， k1=1/（SE），S為絲杠截面積（精確分析時(shí)按中徑，設(shè)計(jì)校核時(shí)也可按底徑算），E為絲杠材料彈性模量；根據(jù)彈性接觸理論，球軸承的軸向接觸變形為［1，4，16］Δ=k2F2/3，k2為軸承軸向接觸變形因數(shù)，與軸承的幾何參數(shù)和材料特性相關(guān)。通常兩端的軸承規(guī)格和數(shù)量不一定相同，即兩端的k2不一定相同，但為了簡(jiǎn)化分析，可按平均值取值。將絲杠、軸承變形計(jì)算式代入式（2），得

結(jié)合式（1），整理后得

式（3）、式（4）即為滾珠絲杠支承系統(tǒng)滾珠絲杠軸承綜合軸向變形與位置坐標(biāo)、軸向負(fù)載的關(guān)系方程組。原理上可從式（4）中解出FA，再代入式（3）得出以x、Fa為變量的Δx函數(shù)表達(dá)式，并可采用極值解法求出Δx最大值及相應(yīng)位置坐標(biāo)，但由于式（3）、式（4）的指數(shù)函數(shù)性質(zhì)，很難求出準(zhǔn)確的解析式和相應(yīng)解。

2 滾珠絲杠軸承綜合軸向變形分析和近似計(jì)算

通過(guò)考察分析可知，式（3）、式（4）的近似解法可有多種，較為實(shí)用的主要有圖線算法和解析式算法。圖線算法是預(yù)先將數(shù)值代入式（3）、式（4）計(jì)算并繪制相應(yīng)圖線簇而形成的方法，應(yīng)用計(jì)算時(shí)，根據(jù)實(shí)際Fa、x從對(duì)應(yīng)圖線中查出FA，再將相對(duì)應(yīng)的x、FA代入式（3）即可求出Δx。由于圖線簇只能是離散的，因此在實(shí)際應(yīng)用時(shí)可能還需采用線性插值法計(jì)算。本方法在作圖、查圖取值和插值計(jì)算過(guò)程都會(huì)存在一定的誤差，而且對(duì)于每一具體結(jié)構(gòu)參數(shù)組都需計(jì)算繪制一簇圖線，且不易求解最大變形量，應(yīng)用不方便。如果能夠建立適用于所有常規(guī)結(jié)構(gòu)參數(shù)的近似解析式計(jì)算方法將更有利于應(yīng)用。

考察式（3）、式（4），難以進(jìn)行方程組解析求解的原因是方程中同時(shí)包含有指數(shù)項(xiàng)k2F2/3A和k2（FA－Fa）2/3，因此尋求近似解析式計(jì)算方法也應(yīng)從這兩項(xiàng)的近似表達(dá)分析著手，并在滿足一定精確程度條件下盡可能簡(jiǎn)單。

2.1 指數(shù)項(xiàng)的近似表達(dá)式

2.1.1 指數(shù)項(xiàng)近似表達(dá)式的初步推導(dǎo)

根據(jù)式（1）、式（2）對(duì)應(yīng)的受力變化關(guān)系，F(xiàn)A隨x單調(diào)遞減，并有

式中，F(xiàn)Amax、FAmin分別為軸承A的最大、最小軸向反力。

式（5）即FA的變動(dòng)范圍。為方便分析，同時(shí)也不影響精確性，可假定絲杠螺母行程等于支承跨距。令yA=k2F2/3A，圖4給出了yA函數(shù)曲線，并以D1D2直線段近似。同時(shí)根據(jù)式（1）得FA－Fa=FB，并令yB=k2F2/3B，即

根據(jù)式（1）、式（5）及臨界預(yù)拉伸力的定義，即最大軸向負(fù)載下絲杠螺母移動(dòng)至末端時(shí)末端軸承正好不出現(xiàn)間隙，得0≤FB≤λFm，因此FB取值范圍在圖4的OD1段。直接按直線段OD1代替相應(yīng)的yB曲線段誤差較大，而采用雙折線OD3-D3D1代替則近似程度更好，其中D3位置的選擇有多種方案。根據(jù)定性分析，通常出現(xiàn)最大綜合軸向變形時(shí)的螺母C位置不出現(xiàn)在靠近兩端的位置，因此，較長(zhǎng)的D3D1段更有利于計(jì)算。

圖4中D1、D2坐標(biāo)值為D1（λFm，k2λ2/3F2/3m）、D2（（1+λ）Fm，k2（1+λ）2/3F2/3m），則直線D1D2方程如下：

yA=c1FA+c2（7）

式中，yA為直線D1D2函數(shù)值。

如圖4選擇D3的橫向位置坐標(biāo)，則D3坐標(biāo)為D3（0.2λFm，0.342k2λ2/3F2/3m），令yB為OD3-

D3D1折線段的函數(shù)值，則

分析D1、D2范圍內(nèi)的函數(shù)值差別如下。令ΔyA=yA－yA，則

式中，τA為相對(duì)誤差率。

顯然式（9）有最大值。對(duì)τA求導(dǎo)并令之為0，得

dτAdFA=c13k2F－23A－2c23k2F－53A=0

將參數(shù)c1、c2值代入，求得相應(yīng)函數(shù)最大值時(shí)的FA，記為FA1：

為簡(jiǎn)便又不失一般性，常規(guī)臨界預(yù)拉伸力系數(shù)λ按0.55～0.75取值［4-5］。代入式（10）、式（9）得τA最大值，記為τAm，范圍為－2%～-2.9% ，與λ為遞減關(guān)系。τAm很小，顯然以直線D1D2近似代替yA曲線段是有效的。參照上述分析方法，式（8）第二式即D1D3段的最大相對(duì)誤差率為τBm=－6.8%，同樣τBm很小，可認(rèn)為近似代替有效。由于OD3段通過(guò)原點(diǎn)，無(wú)法采用相對(duì)誤差率計(jì)算評(píng)定，后面將采用絕對(duì)誤差形式證明其近似有效。

2.1.2 補(bǔ)償修正和最終近似表達(dá)式

根據(jù)圖4形態(tài)及相對(duì)誤差率的分析計(jì)算，可對(duì)式（7）、式（8）進(jìn)行補(bǔ)償修正。將式（10）和λ取值范圍代入ΔyA=yA－yA，得到相應(yīng)的絕對(duì)誤差值ΔyAm的范圍為－（0.021～0.027）k2F2/3m。同樣可算出τBm=－6.8%對(duì)應(yīng)的絕對(duì)誤差ΔyBm的范圍為－（0.026～0.031）k2F2/3m。由于ΔyAm、ΔyBm范圍相對(duì)很小，可按其中間值的1/2作為參考值進(jìn)行補(bǔ)償搜索優(yōu)化，考慮到各端點(diǎn)的關(guān)聯(lián)和相應(yīng)變化，確認(rèn)0.01k2F2/3m為整體補(bǔ)償修正的相對(duì)最佳值，即端點(diǎn)D1、D2、D3及相應(yīng)線段整體上移0.01k2F2/3m（圖5），得到更為精確的最終近似表達(dá)式：

2.1.3 近似計(jì)算誤差

可以驗(yàn)證，考慮D1、D2、D3點(diǎn)，采用式（11）、式（12）計(jì)算的最大相對(duì)誤差率τAm范圍縮小為－1.1%～-1.8%，τBm范圍縮小為－4.3%～-4.6%。根據(jù)式（3）、式（4）中的近似項(xiàng)構(gòu)成，并在誤差估算中可認(rèn)為k1LFA近似等同于k1xFA，將誤差項(xiàng)代入式（3）、式（4）進(jìn)行代數(shù)運(yùn)算，可得對(duì)應(yīng)OD3段時(shí)Δx的最大計(jì)算誤差ΔΔxmax為

ΔΔxmax=（ΔyAmax+Δy′Bmax）－ΔyAmax=Δy′Bmax

式中，Δy′Bmax、ΔyAmax分別為OD3、D1D2段近似的最大誤差。

采用極值求解方法，代入λ值范圍，得

ΔΔxmax=Δy′Bmax=－（0.031～0.039）k2F2/3m

由于OD3段絕對(duì)誤差比D1D3段絕對(duì)誤差要大，因此上述誤差也是Δx的最大絕對(duì)誤差。其中k2F2/3m為軸承的最大獨(dú)立變形量，從而上述誤差相對(duì)于常規(guī)的變形量很小，可滿足正常應(yīng)用要求，因此OD3段也近似有效。

2.2 絲杠軸承綜合軸向變形的解析計(jì)算

整理式（4）、式（11）～式（13）得

式（14）和式（15）即為軸承A軸向反力FA的近似計(jì)算表達(dá)式，F(xiàn)A與x為遞減關(guān)系。將式（14）、式（15）代入式（11），得

將式（16）代入式（3），并整理得

式（17）即為滾珠絲杠支承系統(tǒng)滾珠絲杠軸承綜合軸向變形與螺母位置x的函數(shù)關(guān)系式。式（17）第五式表示參數(shù)v1、v2、v3與變形因數(shù)、臨界預(yù)拉伸力系數(shù)、支承跨距、軸向負(fù)載和最大軸向負(fù)載都有關(guān)系。為便于表達(dá)，v1、v2、v3按復(fù)合參數(shù)形式表示，由式（11）～式（15）、式（17）確定。由于存在兩段取值范圍，Δx隨x的變化呈開口向下的非對(duì)稱弧線形。將式（17）轉(zhuǎn)化為

式（18）即為滾珠絲杠軸承綜合軸向變形Δx與位置x和軸向負(fù)載Fa的雙變量函數(shù)解析式，wi為復(fù)合參數(shù)。應(yīng)用式（18）及復(fù)合參數(shù)計(jì)算式，可以計(jì)算某一負(fù)載作用下任一位置的滾珠絲杠軸承綜合軸向變形量。可以證明，Δx與Fa為單調(diào)遞增關(guān)系。

2.3 滾珠絲杠軸承綜合軸向變形最大值及其位置坐標(biāo)計(jì)算

顯然式（17）存在最大值，假設(shè)滾珠絲杠支承系統(tǒng)滾珠絲杠軸承對(duì)應(yīng)某一Fa的相對(duì)最大綜合軸向變形為Δm時(shí)，螺母位置為xm，根據(jù)極值求解公式得

由于采用復(fù)合參數(shù)形式，在進(jìn)行計(jì)算時(shí)需聯(lián)合求解式（11）～式（15）、式（17）、式（19） ；在u1、u2、u3中間參數(shù)計(jì)算中存在式（14）、式（15）兩個(gè)值域，根據(jù)經(jīng)驗(yàn)，通常情況下Δm、xm計(jì)算滿足式（14）范圍，可先按式（14）計(jì)算和驗(yàn)證值域。根據(jù)式（17）、式（19），Δm與Fa為單調(diào)遞增關(guān)系。當(dāng)Fa=Fm時(shí)，Δm最大，為絕對(duì)最大綜合軸向變形，記為ΔM，相應(yīng)的位置坐標(biāo)xm記為xM。

上述近似解析式算法可適用于所有常規(guī)結(jié)構(gòu)參數(shù)范圍內(nèi)的滾珠絲杠支承系統(tǒng)在取值范圍內(nèi)的任一軸向負(fù)載作用下、在任一位置坐標(biāo)處的滾珠絲杠軸承綜合軸向變形量的直接計(jì)算，以及最大綜合軸向變形及其對(duì)應(yīng)位置坐標(biāo)的直接計(jì)算，且計(jì)算誤差較小，滿足一般應(yīng)用要求，因此相對(duì)于圖線算法，近似解析式計(jì)算方法應(yīng)用更為方便。

3 近似解析式算法的計(jì)算示例和試驗(yàn)分析

3.1 計(jì)算示例

令δB=k1LFm，δT=k2F2/3m，δT、δB分別為最大負(fù)載作用下滾珠絲杠和軸承的軸向變形量，δT/δB為滾珠絲杠軸承最大變形比，表示滾珠絲杠、軸承的變形或剛度大小的關(guān)系，決定臨界預(yù)拉伸力系數(shù)λ［4］。

根據(jù)式（17），求得Δx變化曲線如圖6中實(shí)線。通過(guò)驗(yàn)算，以上計(jì)算符合相應(yīng)FA值域要求。

3.2 試驗(yàn)驗(yàn)證和分析

根據(jù)支承結(jié)構(gòu)原理，對(duì)于一端雙向固定一端單向固定支承形式，當(dāng)負(fù)載作用于滾珠單向固定端時(shí)，其軸向剛度相對(duì)于負(fù)載作用于雙向固定端時(shí)的軸向剛度弱，弱方向特性應(yīng)作為該支承形式的代表特性，而這一弱方向的受力變形特性與兩端單向固定支承形式的受力變形特性相同，因此可以只按兩端單向固定支承形式進(jìn)行試驗(yàn)。

3.2.1 試驗(yàn)參數(shù)

采用可適應(yīng)兩組參數(shù)的裝置進(jìn)行試驗(yàn)。為便于開展試驗(yàn)，兩組參數(shù)主要在于絲杠直徑的不同，從而形成兩組不同的k1和δT/δB值；并按只考慮最大軸向負(fù)載取臨界預(yù)拉伸力，得到不同的λ值。

3.2.2 試驗(yàn)裝置和試驗(yàn)原理

搭建滾珠絲杠支承系統(tǒng)試驗(yàn)平臺(tái)，如圖7所示。在絲杠兩端設(shè)置精密千分表對(duì)絲杠預(yù)拉伸量進(jìn)行測(cè)量，通過(guò)換算確認(rèn)預(yù)拉伸力。采用可移動(dòng)調(diào)整位置的螺旋施力機(jī)構(gòu)和杠桿機(jī)構(gòu)對(duì)絲杠螺母施加軸向作用力，具體作用力可根據(jù)杠桿力平衡方程求出。為了簡(jiǎn)化試驗(yàn)裝置，采用直徑規(guī)格相同、配合間隙較小的T型絲杠螺母副代替滾珠絲杠螺母副，其受力變形效果一致，但可避免施力過(guò)程絲杠螺母副產(chǎn)生逆運(yùn)動(dòng)。采用精密杠桿千分表直接檢測(cè)靠近絲杠螺母兩端、安裝固定在絲杠上的可調(diào)整測(cè)量環(huán)，此方法避開了絲杠螺母的接觸變形。由于施加作用力后可能出現(xiàn)支承座變形，故設(shè)置精密檢測(cè)表對(duì)左支座的右端面進(jìn)行監(jiān)控（圖7中未示出監(jiān)控表）。絲杠螺母處的位置變化（即變形）等于杠桿千分表（圖7中9、12）的變化值均值減去監(jiān)控表變化值。進(jìn)行兩次試驗(yàn)檢測(cè)并取均值。

試驗(yàn)檢測(cè)采集間隔如圖6、圖8所示。進(jìn)行最大軸向變形量及其位置坐標(biāo)檢測(cè)時(shí)，首先根據(jù)式（19）計(jì)算理論xM值，在計(jì)算xM值的附近進(jìn)行加密搜索試驗(yàn)，可找出試驗(yàn)最大值ΔM及其對(duì)應(yīng)位置坐標(biāo)xM。

3.2.3 理論計(jì)算和試驗(yàn)對(duì)比

兩組試驗(yàn)參數(shù)組合下滾珠絲杠軸承綜合軸向變形的數(shù)值計(jì)算和試驗(yàn)結(jié)果見圖6、圖8。最大綜合軸向變形及其位置計(jì)算和試驗(yàn)結(jié)果見表1。

3.2.4 誤差分析

由于理論推導(dǎo)過(guò)程作了近似簡(jiǎn)化，同時(shí)機(jī)械裝置制作存在一定誤差，機(jī)械系統(tǒng)運(yùn)行和試驗(yàn)操作影響因素多且復(fù)雜，如可能出現(xiàn)微小徑向分力及隨機(jī)因素，因此理論計(jì)算和試驗(yàn)值存在一定偏差。本計(jì)算模型采用三折線近似取代指數(shù)曲線，根據(jù)2.1.3節(jié)分析計(jì)算方法，Δx的最大計(jì)算絕對(duì)誤差分別為－0.000 56 mm、－0.000 52 mm，從而最大計(jì)算相對(duì)誤差率為－3.9%、－4.6%。本次試驗(yàn)中精密杠桿千分表經(jīng)過(guò)檢定和扣除系統(tǒng)偏差后，其測(cè)量誤差為0.0005 mm，相對(duì)測(cè)量誤差率分別為4.4%和4.8%，考慮其他環(huán)節(jié)（如軸承與支座接觸面的接觸變形、操作誤差等）的誤差影響，理論計(jì)算和試驗(yàn)對(duì)比存在的誤差是合理的。另外還可以看出，由于本試驗(yàn)裝置絲杠軸承系統(tǒng)本身綜合軸向變形較小，而基本試驗(yàn)操作誤差難以縮小，相對(duì)偏差率較大是正常的，當(dāng)絲杠軸承本身綜合軸向變形較大時(shí)，這一相對(duì)偏差率將減小。同時(shí)，理論計(jì)算和試驗(yàn)值變化趨勢(shì)相同。綜上可知，所推導(dǎo)的解析式計(jì)算方法是合理可行的。

3.2.5 對(duì)比分析結(jié)論

（1）根據(jù)式（11）～式（18），可以針對(duì)在某一軸向負(fù)載Fa作用下，絲杠螺母處于某一位置x時(shí)的軸承反力FA和滾珠絲杠軸承綜合軸向變形Δx進(jìn)行計(jì)算，以及對(duì)相應(yīng)的相對(duì)最大綜合軸向變形Δm及其位置xm進(jìn)行計(jì)算；FA與x為單調(diào)遞減關(guān)系，Δx隨x的變化形態(tài)呈開口向下的非對(duì)稱弧線形；Δm與Fa為單調(diào)遞增關(guān)系，當(dāng)Fa=Fm時(shí)，Δm為最大ΔM。

（2）根據(jù)文獻(xiàn)［4-5］，λ取決于δT/δB。根據(jù)式（19），當(dāng)δT/δB=∞時(shí)λ=1，軸承為相對(duì)完全剛性，可推出xM=L/2；當(dāng)δT/δB=0時(shí)λ=0.35，絲杠為相對(duì)完全剛性，可推出xM=∞，意味著各處綜合軸向變形相等。以上是兩個(gè)極端情況，實(shí)際是不存在的，但可體現(xiàn)變化規(guī)律。

（3）根據(jù)理論計(jì)算和試驗(yàn)結(jié)果分析，當(dāng)δT/δB逐步減小，即λ逐步減小時(shí)，相當(dāng)于滾珠絲杠軸承系統(tǒng)從軸承相對(duì)完全剛性這一極端逐步向絲杠相對(duì)完全剛性這一極端方向變化，Δx變化趨于平緩，xM逐步沿負(fù)載方向離開兩支承跨距的中心。

（4）與近似圖線算法比較，圖線算法也存在一定的誤差，且應(yīng)用相對(duì)不方便；而近似解析式算法雖然存在相對(duì)固定的計(jì)算誤差，但誤差較小，滿足要求且應(yīng)用方便。

4 結(jié)論

（1）絲杠支承系統(tǒng)滾珠絲杠軸承綜合軸向變形的近似計(jì)算可有多種方式，可實(shí)用的有近似圖線算法和本文近似解析式算法，但近似解析式算法應(yīng)用更為方便，便于對(duì)數(shù)控裝備該兩種支承形式進(jìn)給機(jī)構(gòu)的滾珠絲杠軸承綜合軸向變形分布形態(tài)和精度變化特性進(jìn)行細(xì)化分析及精確校核，有利于數(shù)控裝備位置精度的預(yù)測(cè)和運(yùn)行監(jiān)控。

（2）通過(guò)解析計(jì)算和試驗(yàn)對(duì)比分析可知，滾珠絲杠軸承綜合軸向變形隨螺母位置的變化形態(tài)呈開口向下的非對(duì)稱弧線形；當(dāng)絲杠軸承最大變形比逐步減小時(shí)，綜合軸向變形的變化趨于平緩，最大值對(duì)應(yīng)的位置坐標(biāo)逐步沿負(fù)載方向離開兩支承跨距中心。

（3）對(duì)于所推導(dǎo)的近似解析式算法，后續(xù)還可作進(jìn)一步改進(jìn)和擴(kuò)展研究，如增加變系數(shù)誤差修正項(xiàng)及誤差敏感性研究、將其他變形環(huán)節(jié)（如絲杠副滾珠滾道接觸變形）納入計(jì)算模型的研究，以及增加對(duì)一端雙向固定一端單向固定支承形式的試驗(yàn)等。

參考文獻(xiàn)：

［1］ 《現(xiàn)代實(shí)用機(jī)床設(shè)計(jì)手冊(cè)》編委會(huì). 現(xiàn)代實(shí)用機(jī)床設(shè)計(jì)手冊(cè)（上冊(cè)）［M］. 北京：機(jī)械工業(yè)出版社，2006：1833-1836.

Modern Pratical Design Handbook of Machine Tool Write Group. Modern Pratical Design Handbook of Machine Tool（Part One）［M］. Beijing：Mechanical Industry Publishing， 2006：1833-1836.

［2］ 文懷興，夏田. 數(shù)控機(jī)床系統(tǒng)設(shè)計(jì)［M］. 2版. 北京：化學(xué)工業(yè)出版社，2017：132-134.

WEN Huaixing， XIA Tian. Design of CNC Machine Tool System［M］. 2nd ed. Beijing：Chemistry Industry Press， 2017：132-134.

［3］ 武文革，辛志杰，成云平，等. 現(xiàn)代數(shù)控機(jī)床［M］. 北京：國(guó)防工業(yè)出版社，2016：256-257.

WU Wenge， XIN Zhijie， CHENG Yunping， et al. Modern CNC Machine［M］.Beijing：Defence Industry Press， 2016：256-257.

［4］ 張政潑，胡義華，王湘. 絲杠系預(yù)拉伸力的綜合分析計(jì)算與探討［J］. 機(jī)械工程學(xué)報(bào)，2015，51（23）：175-181.

ZHANG Zhengpo， HU Yihua， WANG Xiang. Comprehensive Analysis and Calculation Discuss about Preload Stretching Force of Screw System［J］. Journal of Mechanical Engineering，2015，51（23）：175-181.

［5］ 張政潑，呂勇，徐曉華，等. 現(xiàn)代數(shù)控裝備設(shè)計(jì)［M］. 武漢：華中科技大學(xué)出版社，2022：112-113，130.

ZHANG Zhengpo， LYU Yong， XU Xiaohua， et al.Modern CNC Equipment Design［M］. Wuhan：Huazhong University of Science and Technology Press， 2022：112-113，130.

［6］ 朱永進(jìn). 考慮接觸區(qū)外彈性變形的滾珠絲杠副進(jìn)給系統(tǒng)軸向靜剛度分析［D］. 南京：東南大學(xué)，2021.

ZHU Yongjin. Axial Static Stiffness Analysis of Feed System with Ball Screw Considering Elastic Deformation Outside Contact Zone［D］. Nanjing：Southeast University，2021.

［7］ 史盼盼. 數(shù)控機(jī)床進(jìn)給系統(tǒng)靜剛度匹配設(shè)計(jì)［D］. 天津：天津大學(xué)，2019.

SHI Panpan. Matching Design of Static Stiffness of Feed System of NC Maching Tool［D］. Tianjin：Tianjin University，2019.

［8］ 李帥，胡軍旺. 數(shù)控機(jī)床滾珠絲杠副的系統(tǒng)剛度分析與研究［J］.機(jī)械研究與應(yīng)用，2021，176（6）：1-5.

LI Shuai， HU Junwang. Analysis and Research on the System Stiffness of Ball Screw Pair of CNC Machine Tool［J］.Mechanical Research &Application， 2021，176（6）：1-5.

［9］ 王露郎，王科社，查初亮，等. 滾珠絲杠副軸向靜剛度的建模與研究［J］.組合機(jī)床與自動(dòng)化加工技術(shù)，2015（8）：39-42.

WANG Lulang， WANG Keshe， ZHA Chuliang， et al. Modeling and Analysis of Axial Static Rigidity of Ball Screw［J］. Modular Machine Tool & Automatic Manufacturing Technique， 2015（8）：39-42.

［10］ 宋威. 滾珠絲杠系統(tǒng)軸向剛度分析與研究［J］.現(xiàn)代制造工程，2014（10）：71-75.

SONG Wei. Analysis and Research of the Axial Stiffness of Ball Screw System［J］. Modern Manufacturing Engineering，2014（10）：71-75.

［11］ LIU C， ZHAO C， MENG X， et al. Static Load Distribution Analysis of Ball Screws with Nut PositionVariation［J］.Mechanism & Machine Theory， 2020，151（4）：103893.

［12］ VICENTE D A， HECKER R L， FLORES G M. Ball Screw Drive Systems：Evaluation of Axial and Torsional Deformations［J］. Mecnica Computacional，2009（38）：3265-3277.

［13］ KAMALZADEH A， GORDON D J， ERKORKMAZ K. Robust Compensation of Elastic Deformations in Ball Screw Drives［J］. International Journal of Machine Tools & Manufacture， 2010， 50（6）：559-574.

［14］ 張政潑，呂勇，蔣桂平，等. 滾珠絲杠螺母副附加摩擦力矩分析計(jì)算與研究［J］制造技術(shù)與機(jī)床，2020 （9）：160-164.

ZHANG Zhengpo，LYU Yong， JIANG Guiping， et al.Analysis Calculation and Research on Additional Friction Moment of Ball Screw Mechanism［J］.Manufacturing Technology &Machine Tool， 2020（9）：160-164.

［15］ 孫國(guó)均，趙社戌. 材料力學(xué)［M］.2版. 上海：上海交通大學(xué)出版社，2015：336.

SUN Guojun， ZHAO Shexu. Mechanics of Materials［M］. 2nd ed. Shanghai：Shanghai Jiao Tong University Press， 2015：336.

［16］ 楊咸啟. 接觸力學(xué)引論與滾動(dòng)軸承設(shè)計(jì)分析［M］. 武漢：華中科技大學(xué)出版社，2018：44-47.

YANG Xianqi. Introduction to Contact Mechanics and Design Analysis of Rolling Bearings［M］.Wuhan：Huazhong University of Science and Technology Press， 2018：44-47.