基于動態廣義正交模糊集的多屬性決策方法
柳曉燕,張晨雪,李小南,馮 鋒
(1.西安郵電大學 理學院,陜西 西安 710121; 2.西安翻譯學院 信息工程學院,陜西 西安 710105; 3.西安電子科技大學 數學與統計學院,陜西 西安 710126)
隨著時間的推移,人們在社會經濟活動中面臨著越來越復雜的決策問題。決策中涉及的不確定因素不斷增加,導致處理決策問題所需要的知識在深度和廣度上也隨之提升[1]。經典多屬性決策理論不能有效地刻畫實際決策過程中的復雜性和不確定性,使得現代決策科學愈發重視和發展處理不確定性問題的數學理論和模型,并用其來解決復雜的決策問題。面對這一挑戰,Zadeh[2]在1965年提出了模糊集的概念,以程度化的方式表達和處理不確定性。在處理更復雜的問題時,往往需要從正反兩方面進行考慮,Atanassov為此于1983年提出了直覺模糊集[3]。Xu和Yager[4]將直覺模糊集中各元素的隸屬度和非隸屬度組成的序對稱為直覺模糊數。2013年,Yager[5]松弛了隸屬度和非隸屬度的約束條件,定義了畢達哥拉斯模糊集,并應用于解決實際決策問題。隨后,Yager[6]再次推廣了畢達哥拉斯模糊集的定義,提出了廣義正交模糊集。廣義正交模糊集滿足隸屬度的q次方與非隸屬度的q次方之和不超過1,擴展了直覺模糊集和畢達哥拉斯模糊集的適用范圍,在實際應用中更加靈活方便。
自廣義正交模糊集問世以來,很多學者研究了基于廣義正交模糊集的多屬性決策方法。在廣義正交模糊決策研究中,廣義正交模糊數的比較、排序和集結方法發揮了核心作用。廣義正交模糊數的排序方法可以歸結為兩類:第一類,根據得分函數[7]和精確函數[8]進行排序;第二類,根據基于幾何表示的方法[9-15]進行排序。杜文勝[9]研究了廣義正交模糊數的Minkowski距離,并給出了相關排序方法。在廣義正交模糊信息集結方面,衛貴武等[16]研究了廣義正交模糊數的廣義海倫平均算子和幾何海倫平均算子,并對其相關性質進行了研究。王軍等[17]提出了廣義正交模糊Maclaurin對稱平均算子和廣義正交模糊加權Maclaurin對稱平均算子。杜文勝[18]提出了廣義正交模糊數的算術運算,并研究了一些相關性質。在文獻[19]中,杜文勝又提出了廣義正交模糊加權冪平均算子和廣義正交模糊有序加權冪平均算子,對其基本性質進行了詳細的研究,并將其應用于解決多屬性決策問題。
在實際決策問題中,備選方案往往處于動態變化中,需要考慮備選方案在不同時間段內的動態表現并進行綜合決策。但經典多屬性決策方法僅能對當前狀態下的備選方案進行評價和排序,具有一定的局限性。為此,學者們將靜態的經典多屬性決策問題向動態方向拓展,提出了動態多屬性決策,在理論深度和應用廣度上極大地豐富了多屬性決策研究。一些學者將逼近理想解排序法[20-22](Technique for Order Preference by Similarity to Ideal Solution,TOPSIS)和多準則妥協解法[23-24](VIseKriterijumska Optimizacija I Kompromisno Resenje,VIKOR)等傳統決策方法擴展應用到動態多屬性決策中,在這些研究中集結算子和權重確定方法至關重要。在集結算子研究方面,Xu和Yager[20]提出了動態直覺模糊加權平均(Dynamic Intuitionistic Fuzzy Weighted Averaging,DIFWA)算子,并結合基于Minkowski距離的TOPSIS法研究了動態直覺模糊多屬性決策方法。權重的確定方法包括屬性權重和時間權重兩方面:屬性權重客觀確定方法包括離差最大化法[25]、熵權法[26-27]和主成分分析法[28]等;時間權重確定方法[29]包括基本單位區間單調(Basic Unit-interval Monotonic,BUM)函數法、正態分布法和指數分布法等。此外,部分學者認為集結過程會造成信息損失,通過構建評價模型[30-31]進行綜合計算,以此解決動態多屬性決策問題。
目前,現有文獻中對廣義正交模糊環境下的動態多屬性決策方法鮮有探索。為此,擬著重關注動態廣義正交模糊集及其在動態多屬性決策中的應用。首先,給出動態廣義正交模糊集及其基本運算的定義。然后,在動態廣義正交模糊環境下探索決策信息的集結問題,提出一種動態廣義正交模糊多屬性決策方法。最后,將所提決策方法應用于5G通信企業評估問題,并通過對比分析驗證其合理性。
1 預備知識
模糊集、直覺模糊集、畢達哥拉斯模糊集、廣義正交模糊集及其運算等基礎知識概述如下,若無特殊說明,論域均表示為U。
1.1 模糊集與畢達哥拉斯模糊集
定義1[2]映射μ:U→[0,1]稱為論域U中的一個模糊集。表示模糊集的映射μ稱為隸屬函數,稱μ(u)為u對于μ的隸屬度,用于量化u屬于μ的程度。
定義2[3]論域U上的直覺模糊集定義為
I={(u,tI(u),fI(u))|u∈U}
式中:映射tI:U→[0,1]和fI:U→[0,1]分別稱為I的隸屬函數和非隸屬函數;函數值tI(u)和fI(u)分別稱為u對于I的隸屬度和非隸屬度,且滿足0≤tI(u)+fI(u)≤1。
定義3[5]論域U上的畢達哥拉斯模糊集定義為
P={(u,tP(u),fP(u))|u∈U}
1.2 廣義正交模糊集
定義4[6]論域U上的廣義正交模糊集定義為
G={(u,tG(u),fG(u))|u∈U}
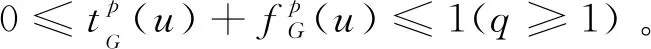
定義5[6]論域U上的廣義正交模糊集
A={(u,tA(u),fA(u))|u∈U}B={(u,tB(u),fB(u))|u∈U}
的交、并、補運算分別定義為
A∩B={(u,min{tA(u),tB(u)},max{fA(u),fB(u)})|u∈U}A∪B={(u,max{tA(u),tB(u)},min{fA(u),fB(u)})|u∈U}A′={(u,fA(u),tA(u))|u∈U}
定義6[6]設

其中,(a1,a2)和(b1,b2)為廣義正交模糊數。
廣義正交模糊數的一些基本運算定義如下。
定義7設A=(a1,a2)和B=(b1,b2)是廣義正交模糊數,若λ為任意正實數,則有
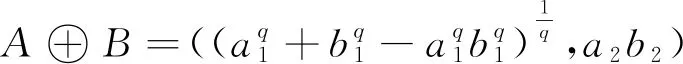
2 動態廣義正交模糊集
設GOFSq(U)表示U上全體廣義正交模糊集構成的類。將(U,T)稱為動態論域,其中T是與U中對象關聯的所有時間參數構成的集合,稱為時域空間。應當注意,即使U是有限集時,T也可以是一個無限集。
定義8二元組I=(ω,A)稱為論域U上的一個動態廣義正交模糊集,其中A?T稱作I的時間參數集,映射ω:A→GOFSq(U)(q≥1)稱為I的動態近似函數。
通過引入時間參數,動態廣義正交模糊集給出了動態不確定概念在不同時刻的靜態近似描述。對任意的t∈A,稱ω(t)∈U為I的t-近似元集。
為了更好地描述和處理廣義正交模糊環境下的動態決策問題,下面將廣義正交模糊集的運算進行動態擴展。
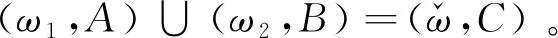


定義12設I=(ω,A)是論域U上的一個動態廣義正交模糊集,λ為任意正實數。λ和I的標量積為一個動態廣義正交模糊集Ω=λI=(θ,A)。?t∈A和?u∈U,Ω的動態近似函數θ定義為

(1)
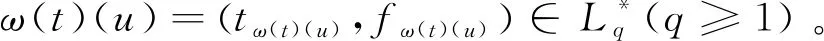
3 動態廣義正交模糊多屬性決策
3.1 動態廣義正交模糊信息集結方法
定義13設(P1,≤1)和(P2,≤2)為兩個偏序集,P1×P2上的字典序定義為
(a1,b1)≤(a2,b2)?(a1<1a2)∨(a1=a2∧b1≤2b2)
其中,(a1,b1),(a2,b2)∈P1×P2。
下面將文獻[32]中直覺模糊數的字典序定義推廣至廣義正交模糊數的范疇,具體如下。
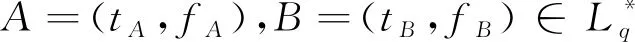
(2)
在廣義正交模糊決策中,集結算子可將一組輸入數據融合為一個輸出數據,其定義如下。


條件2f(a1,a2,…,an)=(0,1),其中ai=(0,1) (i=1,2,…,n)。
條件3f(a1,a2,…,an)=(1,0),其中ai=(1,0) (i=1,2,…,n)。

條件1a1≤b1∧…∧an≤bn?
f(a1,a2,…,an)≤f(b1,b2,…,bn)


Ωw(a1,a2,…,an)=w1a1⊕w2a2⊕…⊕wnan
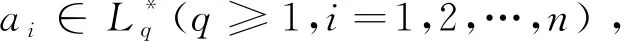
根據定義17,用數學歸納法可證關于GOFWA算子的如下結論。
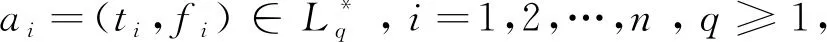

(3)
其中,w=(w1,w2,…,wn)T是權重向量。

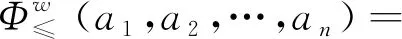
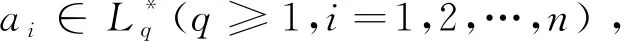

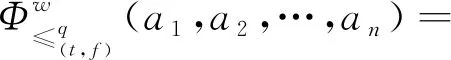
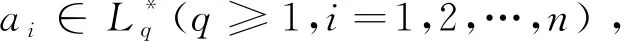

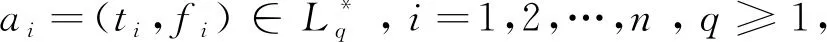
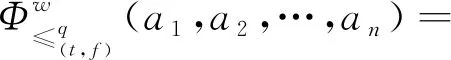
(4)
其中,w=(w1,w2,…,wn)T是算子權重向量。

證明根據定義16,分別證明以下兩個條件。
條件1考慮算子集結后仍是一個廣義正交模糊數,分別令
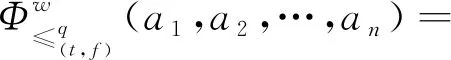

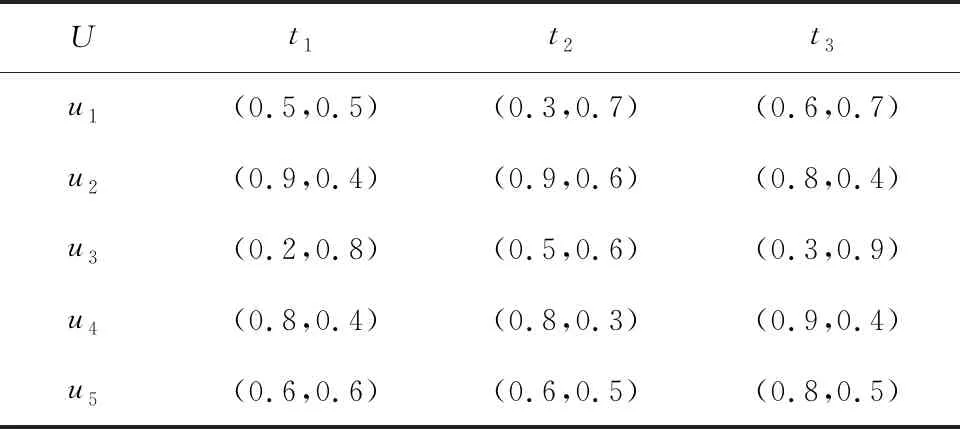
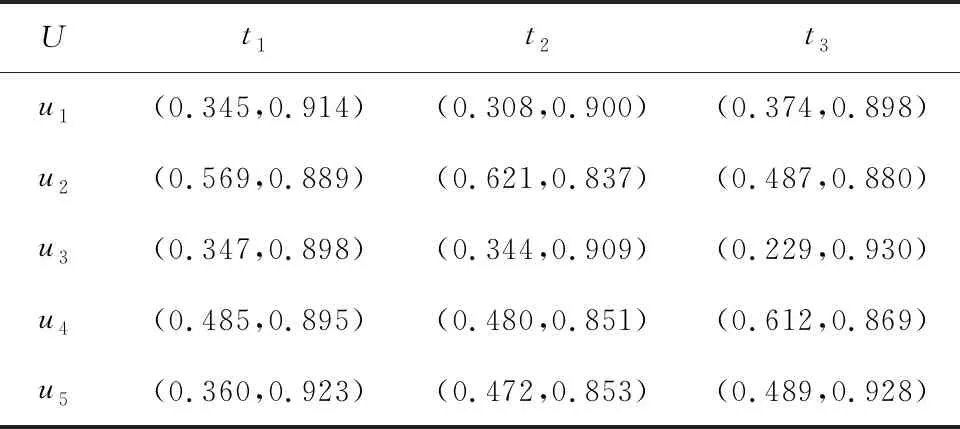
設共有k組ai和bi滿足ti 情況1若k≠0,則tσ(i)≤uσ(i)(i=1,2,…,n)(當k=n時,有tσ(i) 于是, 因此, 情況2若k=0,則tσ(i)=uσ(i)∧fσ(i)≥vσ(i)。類似情況1中的推導過程,可得 條件2根據廣義正交模糊數的交與并的定義,分別令 再根據其單調性可得 其中, 且i=1,2,…,m,j=1,2,…,n,k=1,2,…,l。 由定義20和定理2,可以證明如下結論。 定理4設I=(ω,A)是動態有序加權平均廣義正交模糊集,則可計算其動態近似函數 ω(tj)(ui)= (5) 其中, 其中,q≥1且i=1,2,…,m。 由定義21和定理1,可證如下結論。 定理5給定論域U={u1,u2,…,um}上一個動態廣義正交模糊集I=(ω,A),其中時間參數集A={t1,t2,…,tn},且 (6) (7) 考慮到不同時間段內,不同屬性的重要程度也會隨之變化,因而應給不同時間段的屬性不同的權重值。為此,下面采用文獻[25]中的最大偏差法確定屬性權重。屬性評價值均為廣義正交模糊數,選擇常用的漢明距離度量偏差。兩個q階廣義正交模糊數a=(a1,a2)和b=(b1,b2)之間的漢明距離為 (8) 在tj(j=1,2,…,n)時刻屬性ek(k=1,2,…,l)下所有備選方案的屬性評價值的偏差之和為 (9) 如果每個備選方案的評價值在某個屬性下偏差和較小,即幾乎沒有差異,則表明該屬性在方案排序過程中的作用較小,應被賦予較小的權重;相反,如果某個屬性的評價值偏差和較大,則該屬性在方案排序中有重要作用,應分配較大的權重。在此僅考慮屬性權重信息完全未知的情況,根據上述思想,即求解優化模型獲得屬性權重,優化模型為 (10) 而后將求得的屬性權重進行歸一化,即可得到屬性權重 基于廣義正交模糊集的多屬性決策方法中,階數q大多采用了直接指定的處理方式。這種方式依賴于決策者的主觀判斷,會在一定程度上對決策結果的客觀性產生影響。如何給出確定階數的合理方法是一個重要問題。Riyahi等提出了一種確定廣義正交模糊集的合理階數的基本策略[34]。借鑒文獻[34]中的思想,下面給出一種簡便方法,以便在實際應用中確定動態廣義正交模糊集的階數q。 設I=(ω,A)是論域U上的動態廣義正交模糊集,A為時間參數集。記 ω(a)(u)=(tω(a)(u),fω(a)(u)) 其中,a∈A且u∈U。令 (11) 當階數q滿足條件Mq+Mq≤1時,I中所有廣義正交模糊數均可滿足對應的約束條件。由此可得 (12) 為降低冪運算造成的信息損失,實際應用中可選取使上式成立的最小正整數作為動態廣義正交模糊集的最優階數。 I(k)=(ω(k),T) (k=1,2,…,l) 記其動態近似函數為 基于GOFOWA算子的動態廣義正交模糊多屬性決策方法的流程如圖1所示,具體步驟如下。 圖1 動態廣義正交模糊決策方法流程 步驟1根據給定的動態決策信息在論域U上建立l個動態廣義正交模糊集 步驟2將屬性集合E按照效益型屬性和成本型屬性劃分為兩個不相交的子集Eb和Ec。 步驟6給定廣義正交模糊有序加權平均算子的算子權重w=(w1,w2,…,wl)T。 步驟8利用時間熵最大化方法確定時間權重向量η=(η1,η2,…,ηn)T。 運用數值實例與現有方法進行比較,驗證所提動態廣義正交模糊多屬性決策方法的合理性。 5G是第五代移動通信技術的簡稱,其并不是一種獨立的、全新的無線接入技術,而是現有無線接入技術(包括2G、3G、4G和WiFi)的演進,以及通過集成一些新的互補無線接入技術形成的解決方案的總稱[35]。與傳統的通信技術相比,5G是一種將多種通信技術相結合的綜合性新技術,具有速度快、流量密度高、時延短、能效高、支持海量連接及增強移動寬帶等諸多優點。5G技術優勢顯著,其將帶動多行多業的發展,且具有非常廣闊的應用前景。運營商選擇5G通信企業合作伙伴時,會先從多個方面對企業的5G通信產品進行評估,再綜合各項評價給出最優選擇。在此過程中,需要有合理、可靠的評估指標為決策過程提供支持,以保證決策結果的科學性和可用性。 選用文獻[35]中的e1、e2、e3、e4和e5等5個指標作為評估的關鍵因素,其中:e1表示峰值數據速率,描述了最大可實現數據速率;e2表示用戶體驗的數據速率,描述了覆蓋區域可實現數據速率;e3表示區域流量容量,描述了覆蓋區域總流量;e4表示能量效率,描述了每單位能耗發送/接收的數據;e5表示延遲,描述了數據包在網絡中傳輸的延遲時間。 設論域U={u1,u2,…,u5},其中ui(i=1,2,…,5)分別代表三星、中興、愛立信、華為及諾基亞。某運營商計劃從這5家領先的5G企業中選擇一家進行合作。將上述5個指標構成的屬性集記作E={e1,e2,e3,e4,e5},時域空間記為T={t1,t2,t3},并取時間參數集A=T。專家將從t1(2018年)、t2(2019年)和t3(2020年)等3個時段依照上述5個評價指標對待選企業進行評估。根據指標含義,指標e1、e2、e3、e4均為效益型屬性,指標e5為成本型屬性。專家打分通過轉換處理后均以廣義正交模糊數的形式量化,如表1所示。 表1 動態廣義正交模糊集 利用所提動態廣義正交模糊多屬性決策方法求解步驟如下。 步驟2將屬性集合E按照效益型屬性和成本型屬性劃分為兩個不相交的子集Eb={e1,e2,e3,e4}和Ec={e5}。 表2 動態廣義正交模糊集I(5)=(ω(5),T) 步驟4根據式(12)分別求出動態廣義正交模糊集I(k)(k=1,2,3,4,5)的最優階數分別為 步驟5根據式(8)和式(9)求得在tj時刻屬性ek下所有待選企業之間決策信息評估值的偏差之和分別為 將上述結果代入式(10)求解優化模型 求得的權重向量分別為 經過歸一化處理后,分別得到tj(j=1,2,3)時刻下的3個屬性權重向量分別為 w(1)=(0.073 6,0.108 2,0.037 5,0.093 4,0.687 4)Tw(2)=(0.326 5,0.077 5,0.027 9,0.125 9,0.442 2)Tw(3)=(0.023 2,0.282 8,0.022 5,0.052 6,0.618 9)T 步驟6取態度特征值為0.1,計算可得GOFOWA算子的算子權重為 w=(0.347,0.277,0.214,0.124,0.038)T 2)將5個加權動態廣義正交模糊集Ω(k)=(θ(k),T)中的廣義正交模糊數進行排序,使 成立,其中i=1,2,…,5,j=1,2,3,k=1,2,3,4,5,且(σ(1),σ(2),…,σ(5))為(1,2,3,4,5)的一個置換。 3)根據定義20和式(5),利用算子權重w=(w1,w2,w3,w4,w5)T將置換后得到的5個加權動態廣義正交模糊集集結為1個動態有序加權平均廣義正交模糊集I=(ω,T),如表3所示。 表3 動態有序加權平均廣義正交模糊集I=(ω,T) 步驟8假設決策者在各時段數據中較重視近期數據,根據文獻[33]中時間度的標度參考表,取時間度λ=0.3,根據式(7)求解非線性規劃模型 可得到時間權重向量為η=(0.15,0.30,0.55)T。 步驟9根據定義21和式(6),由η和I求得時間加權平均廣義正交模糊集分別為 G(u1)=(0.356,0.901)G(u2)=(0.560,0.868)G(u3)=(0.311,0.919)G(u4)=(0.581,0.868)G(u5)=(0.473,0.904) u4?u2?u5?u1?u3 根據偏好排序結果給出決策建議,在當前決策環境下,建議選擇的合作企業是華為。 為了研究階數q對方法結果的影響,現保持上述其余變量不變,僅改變階數q的取值,所得排序結果如表4所示。 表4 不同階數q下的排序結果 從表4排序結果可見,q=3時的排序與其余結果存在些許差異,而由式(12)所確定范圍內的階數q對應的排序結果完全一致,這表明3.2節中所提最優階數的確定方法是合理的。 各種方法所得排序結果如表5所示。 表5 不同決策方法的結果比較 由表5中的排序結果可見,所提方法與文獻[20]和文獻[21]中動態多屬性決策方法給出的排序結果基本一致,u4和u2在排序中均處于前兩位,u3均處于最末位。排序結果存在微小差異的原因在于文獻[20]和文獻[21]使用直覺模糊集或畢達哥拉斯模糊集描述決策信息,而4.2節中的部分數據并不滿足直覺模糊集或畢達哥拉斯模糊集的約束條件。所提方法先結合屬性權重計算加權動態廣義正交模糊集,然后綜合考慮各個時刻對備選方案整體評價的影響,且評價信息的表示由直覺模糊集或畢達哥拉斯模糊集擴展為動態廣義正交模糊集,擴大了相關決策方法的應用廣度和深度。 文獻[9]中方法基于Minkowski距離計算備選方案的貼近度(即備選方案遠離負理想且接近正理想的程度)并給出方案排序。參數p不同時,分別對應漢明距離(p=1)、歐幾里得距離(p=2)和切比雪夫距離(p=∞),對應排序結果略有差異。由于文獻[9]方法并未考慮時間因素的影響,其排序結果與上述方法相比差別較大。文獻[35]在畢達哥拉斯模糊環境下擴展了CoCoSo多屬性決策法,該方法與所提方法的排序結果基本一致,均認為u4是最優方案,u3是最劣方案。與文獻[9]和文獻[35]相比,所提方法考慮了時間因素對決策過程的影響,能夠捕捉不同時刻決策信息的變化,從而做出更符合實際情況的科學決策。 考慮到在實際決策環境中,備選方案在不同時刻的重要性往往處于動態變化之中,因此,對廣義正交模糊集進行動態擴展,定義了動態廣義正交模糊集及其基本運算。利用動態廣義正交模糊集和廣義正交模糊有序加權平均算子,提出了動態廣義正交模糊環境下的一種多屬性決策方法。該決策方法考慮了時間因素對決策過程的影響以及不同時間段內決策信息的重要程度,充分反映了專家對備選方案的總體評價隨時間變化的特點。最后,通過5G通信企業評估問題驗證了所提方法的有效性,并與現有幾種方法進行了對比分析,結果表明,基于動態廣義正交模糊集的多屬性決策方法考慮了時間因素對決策過程的影響,能夠動態捕捉不同時刻決策信息的變化,從而做出更符合實際情況的科學決策。 上述研究僅將動態廣義正交模糊集與GOFOWA算子進行結合,今后可嘗試將其他算子與動態廣義正交模糊集相結合,提出更符合實際應用需求的動態多屬性決策方法。






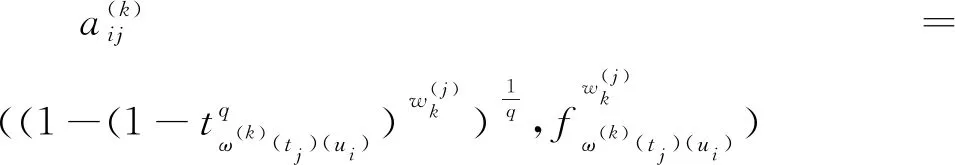
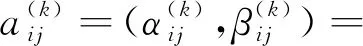
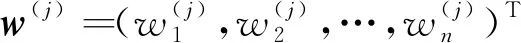



3.2 動態廣義正交模糊多屬性決策方法











4 算例分析
4.1 5G通信企業評估問題
4.2 問題求解
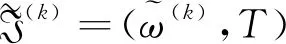

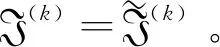


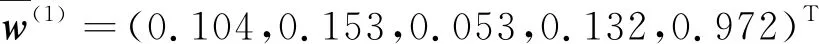








4.3 對比分析


5 結語

