基于監督學習的信息繭房減弱方案研究

黃 之,許學裔,吳佳澤,徐超陽,吳培榕,孟慶欣

(湖州師范學院 理學院,浙江 湖州 313000)

0 引 言

信息繭房(informationcocoons)是由哈佛大學教授凱斯·桑斯坦提出的一個概念,是指人們的信息領域習慣性地被自己的興趣所引導,從而將自己的生活桎梏于像蠶繭一般的“繭房”中的現象[1].隨著互聯網和信息技術的發展,用戶獲得的信息越來越窄化、個性化,信息繭房現象也越趨于明顯.國外對信息繭房的研究較早,西方學者更傾向于認為信息繭房可能只是“一個擔憂”和“不準確的預言”,真正的信息繭房可能并不存在.在政治領域,西班牙學者Cardenal通過研究西班牙媒介系統發現,用戶獲取的信息呈現多元化;在社會領域,印度數學科學家和英國學者認為,假新聞能夠通過“信息繭房”進行傳播,甚至很多帶有情緒偏見的信息也能夠通過信息繭房進行傳播,給社會帶來極大的危害.而國內學者對信息繭房更傾向認為其真實存在且不能隨意地將概念外延.最明顯的概念外延現象是在“信息繭房”與“過濾氣泡”這兩大概念上的混用.合理的概念外延有利于掌握信息繭房的范圍和打破信息桎梏.目前,國內有關信息繭房的研究較多[2-7],主要停留在利用問卷調查、SPSS等統計軟件進行統計分析,并針對個案提出一些改進措施.例如,徐翔等利用BERT模型,以新浪微博用戶為例,實證檢視社交網絡內容生產中的用戶“繭房趨同性”現象[8];張禹基于SOR理論,以高校大學生為研究對象,實證信息繭房對傳統文化認同的影響[9];崔椒潔等通過引入正當程序規則限制數據挖掘機構的數據權力,建立數據挖掘機構與個人信息主體之間有效互動的通道和程序,以助于實現對個人信息的保護[10];彭曉曉利用內容分析方法和社會網絡分析方法,以廣告業界和學界為例,證實桑斯坦提出的“信息繭房”效應的存在[11];任秋菊通過數據分析,以新冠病毒疫情為例,證實日常生活信息查詢行為表現出較強的社會網絡依賴[12].這些研究都受限于一定群體,不能很好地反映信息繭房的實際存在.因此,如何盡可能地規避信息繭房,削減信息繭房效應的消極作用,這是本文的研究重點.尤其是對信息高速流通和發展的浙江省,如何從用戶角度出發建立數學模型,是本文的創新與特色.

1 基于機器學習的模型

目前,在信息繭房預測模型的研究中,大多只采用單一的算法建立模型,如支持向量機等.本文通過隨機森林、支持向量機、樸素貝葉斯3種模型的對比分析,選取最優模型,建立信息繭房預測模型;采用adaboost、GBDT集成學習方法構建信息繭房與系統主導模式/用戶主導模式之間的Boosting集成回歸模型,并比較兩個模型的評估指標,最終得出最優模型.

1.1 SVM算法

支持向量機模型(SVM)是一種二分類模型,它的基本模型是定義在特征空間上間隔最大的線性分類器.它能非常成功地處理回歸問題(時間序列分析)、模式識別(分類問題、判別分析)等問題,并可推廣應用于預測和綜合評價等領域.例如,葉林等利用支持向量機法的結構風險最小化原則,建立了短期風電功率組合預測模型[13];袁勝發等研究了支持向量機在機械故障診斷中的應用[14].

1.2 樸素貝葉斯算法

樸素貝葉斯算法是基于特征條件獨立假設和貝葉斯定理的一種分類算法.首先,基于特征條件獨立假設,對已給定的訓練數據集學習輸入輸出的聯合概率分布;其次,基于此模型,利用貝葉斯定理求使得實例X后驗概率最大的輸出y.例如,范慧芳等在考慮特征屬性與類別之間,以及各特征屬性之間的依賴關系的基礎上,利用ReliefF算法和相關系數法分別對特征屬性進行加權處理,構造了一個基于樸素貝葉斯定理的改進的樸素貝葉斯網絡模型[15].

1.3 隨機森林算法

隨機森林模型(RF)是先利用重采樣技術,從原始訓練樣本集N個樣本中隨機抽取k個樣本進行替換,生成一個新的訓練樣本集,然后生成k個分類樹,最后形成基于自助樣本集的隨機森林.當需要對某個樣本進行預測時,先統計森林中每棵樹對該樣本的預測結果,然后通過投票法從這些預測結果中選出最后的結果.單一決策樹簡單的分類能力被龐大數量的森林結構綜合起來,最終的分類結果經投票選取后,比單棵決策樹的準確率及效率大大提高.例如,張雷等利用RF處理預測變量數目極大且超過觀測值數目這類情況,并對其進行云南松分布模擬研究[16];賴成光等基于RF構建洪災風險評價模型[17].

1.4 Boosting算法

提升樹模型是機器學習中處理分類問題的常用方法之一.其基本思想是:增加前一個基學習器在訓練過程中預測錯誤樣本的權重,使后續基學習器更加關注這些打標錯誤的訓練樣本,以盡可能地糾正這些錯誤,從而一直向下串行直至產生需要的T個基學習器,最終對T個基學習器進行加權結合,產生集成學習器.例如,馮中華等利用梯度提升樹算法實現了一個高校的DGA域名檢測模型[18].

2 特征選取與數據預處理

特征選取與數據預處理流程見圖1.

2.1 特征選取

將X的特征名稱設為年級、性格、擁有電子產品的數量、興趣廣泛程度、用戶心理指標1～4、用戶行為指標1～7、用戶信息素養1～4、系統習慣導向1～3、信息相關性1～4、技術智能程度1～3.將Y的特征名稱設為類型.

2.2 樣本來源

根據所選取的特征,針對浙江省高校學生初步設計調查問卷,并發放80份問卷進行前期預調查.依據預調查結果對問卷不合理處做出改進,形成最終問卷.利用最終問卷,通過線上與線下相結合的方式進行問卷調查,共發放問卷500份,回收500份,其中有效問卷481份,男生300份、女生181份,有效回收率為96.2%.本文將以問卷結果轉化所得的數據作為數據樣本.

2.3 ADASYN處理失衡數據

對本文所研究的二分類問題進行數據分析,發現標簽為0的一類占比為70.1%,標簽為1的一類占比為29.9%,兩者差異高達40.2%,數據樣本嚴重失衡.因此,本文采用ADASYN算法對失衡數據進行處理.

ADASYN算法是在SMOTE(Synthetic Minority Over-sampling Technique)算法的基礎上提出的一種自適應的合成樣本生成算法,相當于一種插值算法.其基本思想為:根據每個少數類樣本周圍的分布密度決定生成合成樣本的數量.首先,計算每個少數類樣本周圍的密度;然后,根據所得的密度確定生成合成樣本的數量,密度越大的樣本生成的合成樣本越多,越能夠準確反映數據集的分布情況.

ADASYN算法的具體數據采樣過程為:

對m個樣本的數據集{xi,yi},i=1,2,…,m,其中xi為n維特征空間X中的一個實例,yi∈Y={1,-1}是與xi相關的類別識別標簽.將ms和mi分別定義為少數類樣本和多數類樣本.因此,ms≤ml,且ms+ml=m.

第一步,計算數據樣本不平衡程度,d=ms/ml,d∈(0,1].

第二步,計算需要為少數類樣本生成的合成樣本數量,G=(ml-ms)×β,其中β為一個參數,可在生成合成數據后指定所需的平衡水平.若β=1,則表示創建了一個完全平衡的數據集.

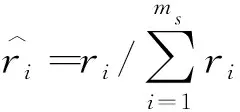
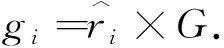
第五步,從數據xi的K個最近鄰中隨機選擇一個少數類樣本xzi,通過公式si=xi+(xzi-xi)×λ產生合成樣本,其中λ∈[0,1]為一個隨機數,(xzi-xi)為n維空間中的差異向量.

預處理前后數據對比見表1.

表1 非平衡數據與平衡數據對比

通過ADASYN算法對數據樣本預處理后,標簽為0的一類占51.6%,標簽為1的一類占48.4%,數據達到均衡標準.

2.4 消融實驗

為提升模型的預測準確率,本文進行特征工程、數據樣本的平衡工作.下面利用GBDT模型進行消融實驗,以驗證特征工程和樣本數據的平衡是有效的.

原始模型評估結果見表2.

表2 利用原始數據建立的GBDT模型的評估結果

實驗1:在建立GBDT模型的基礎上加特征工程,模型評估結果見表3.

表3 已進行特征工程的數據建立的GBDT模型的評估結果

實驗2:在建立GBDT模型的基礎上加對樣本數據的平衡,模型評估結果見表4.

表4 已平衡的樣本數據建立的GBDT模型的評估結果

實驗3:在建立GBDT模型的基礎上加特征工程和樣本數據的平衡,模型評估結果見表5.

表5 已進行特征工程和平衡的數據建立的GBDT模型的評估結果

結果表明,實驗1和實驗2的模型效果都低于實驗3,說明同時進行特征工程和樣本數據的平衡工作對GBDT模型的提升是有效的.

3 模型的建立與分析

在構建和使用信息繭房的監督學習預測模型和集成回歸模型前,將信息繭房問卷數據集劃分為訓練集和測試集,訓練集與測試集的比例為7∶3.本研究采用多模型比較分析選取最優模型.

3.1 信息繭房預測模型的建立與分析

信息繭房預測模型流程見圖2.

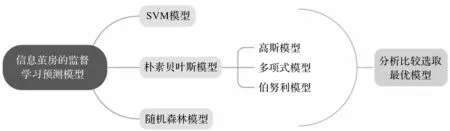
圖2 信息繭房預測模型流程

3.1.1 樸素貝葉斯預測模型的構建與分析

首先,構建樸素貝葉斯的3種不同模型,即高斯模型、多項式模型、伯努利模型.針對這3種不同模型,對數據進行分析處理:由于數據特征都為離散類型,所以通過對特征概率的平滑處理,構建多項式模型;由于數據集的一些特征不符合高斯分布,所以通過平方根變化使特征數據正態化,構建高斯模型;由于離散數據變量取值不同,所以通過定義一個二值化方法將輸入特征值二值化,構建伯努利模型.然后,將包含多個實例點的X_testset傳入構建好的貝葉斯模型預測函數中,對測試數據點進行預測劃分,并將返回值存儲到對應的文件名稱中.最后,通過metrics.accuracy_score函數計算3種貝葉斯模型的預測精度.

通過分析得到,高斯模型在訓練集上的預測準確率最高,為0.74;伯努利模型和多項式模型在訓練集上的預測準確率相對較低,分別為0.54和0.62;高斯模型在測試集上的預測準確率最高,為0.63.針對伯努利模型,通過調整binarize參數值發現,當binarize參數值太大或太小時,伯努利模型的預測準確率呈斷崖式下降,見圖3.因此,參數值的選取必須在樣本集所有特征值的最小值和最大值之間.圖3中,當binarize值在4.5附近時,伯努利貝模型的預測準確率較高.

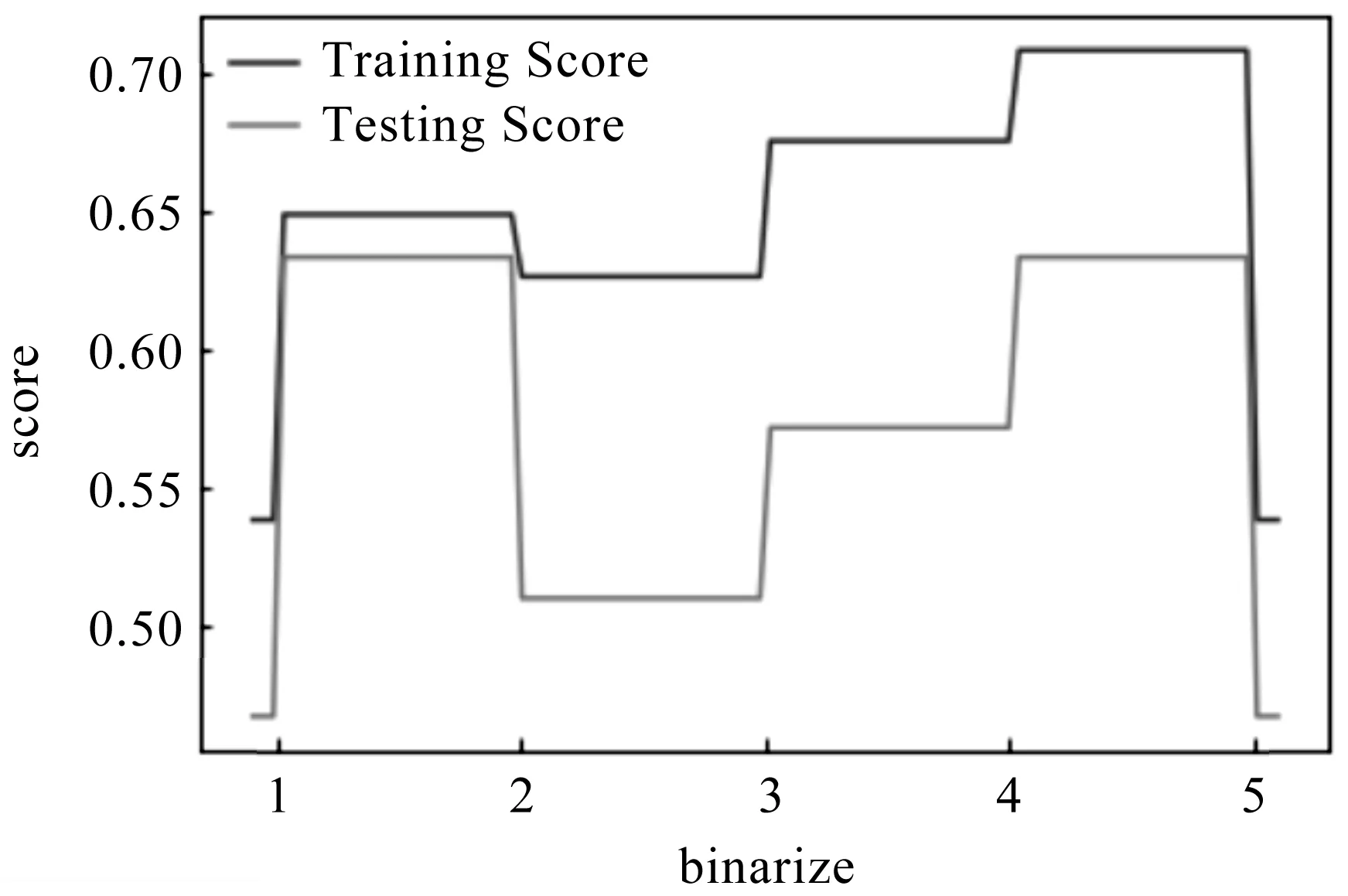
圖3 不同參數值下伯努利模型的預測準確率

3.1.2 SVM預測模型的構建與分析

由于問卷數據具有線性不可分性,所以本文選用非線性支持向量機模型.本研究在Mercer定理的基礎上選取徑向基函數(RBF)作為核函數,將低維空間中算得的數據輸入空間映射到高維特征空間,構造最優超平面,并對構建模型分類規律的可靠性進行檢驗.SVM模型評估結果見表6.

表6 SVM模型評估結果

3.1.3 隨機森林預測模型的構建與分析

利用RandomForestClassifier()模型,構建信息繭房預測模型.其步驟為:

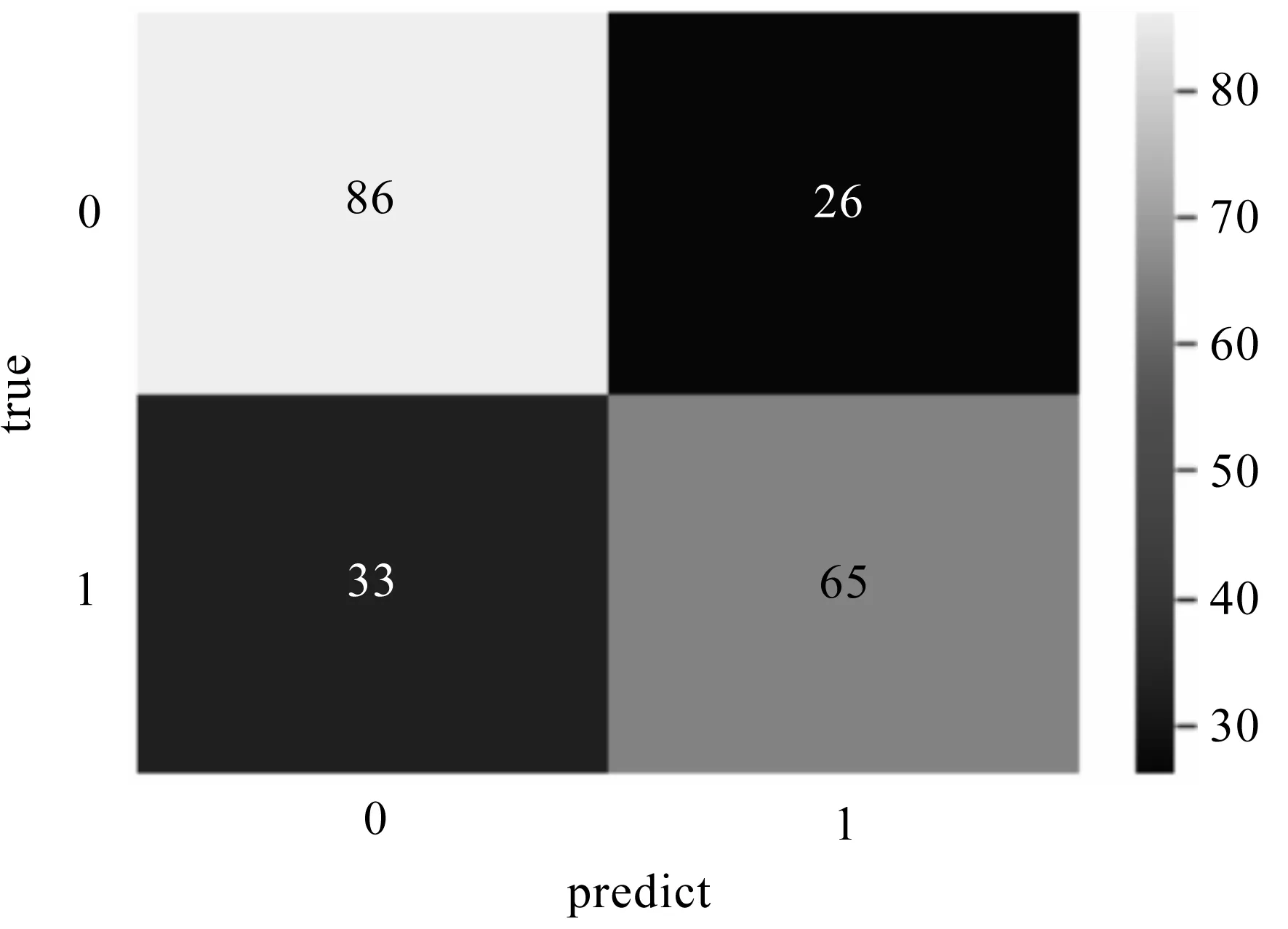
圖4 隨機森林模型混淆矩陣圖

(1)對浙江省高校學生信息繭房問卷數據進行導入,并獲取響應變量和特征矩陣;

(2)將數據集劃分為70%訓練集和30%測試集;

(3)用訓練特征矩陣和訓練響應變量訓練并構建隨機森林信息繭房預測模型;

(4)使用已構建的模型對測試集進行預測,并比較預測值與實際值;

(5)計算模型預測的精度.

繪制成的隨機森林模型混淆矩陣見圖4.混淆矩陣的對角線元素為預測正確的樣本量.由圖4可得,隨機森林模型的預測準確率為72%.

3.1.4 3種信息繭房預測模型的比較

通過分析發現,支持向量機模型在訓練數據集上的模型準確率、召回率、精確率和F1均比在測試集上的高,說明該模型在測試集上的預測損失較大,存在過擬合現象.雖然支持向量機模型有利于解決特征空間較大的機器學習問題,但當觀測樣本較多時,其預測的效率并不高.因此,本文不選用支持向量機模型.

通過分析隨機森林模型和樸素貝葉斯模型發現,隨機森林模型的預測準確率為72%,略低于高斯模型的預測準確率.其原因可能是:訓練數據及測試數據中有許多特征屬性的取值太多,如問卷中有許多量表題的取值都是1～5,這會對隨機森林模型的分類預測結果產生影響,因此隨機森林對這些數據產生的屬性權值不能完全采用;而高斯模型通過計算樣本數據的概率分布對其分類,量表中的取值對其影響較小,且高斯模型的處理效率較高,在信息繭房預測中的準確率高達74%.因此,本文選用高斯模型作為信息繭房的預測模型.

3.2 信息繭房集成回歸模型的建立與分析

信息繭房集成回歸模型流程見圖5.

3.2.1 提升樹模型的建立

分別利用adaboost、GBDT模型,將用戶心理指標1～4、用戶行為指標1～7、用戶信息素養1～4、系統習慣導向1～3、信息相關性1～4、技術智能程度1～3作為特征,學習率設為1,構建是否處于信息繭房與系統主導模式和用戶主導模式之間的集成回歸模型.

3.2.2 提升樹模型的結果

從adaboost模型特征篩選結果看,感興趣信息所在的頁面內容安排模式是類似的特征重要性為10%(最大特征重要性為20%),對判斷是否處于信息繭房起到重要作用.

通過繪制adaboost混淆矩陣檢驗模型的預測準確性,混淆矩陣見圖6.混淆矩陣的對角線元素為預測正確的樣本量[7].adaboost模型評估結果見表7,adaboost模型測試數據評估結果見表8.

表7 Adaboost模型評估結果

表8 Adaboost模型測試數據評估結果

從GBDT模型特征篩選結果看,推送信息與自己日常生活聯系的特征重要性為6.9%(最大特征重要性為7%),不能快捷準確地讀取自己獲得信息的特征重要性為6.9%(最大特征重要性為7%).這些重要特征對判斷是否處于信息繭房起關鍵作用.

通過繪制GBDT混淆矩陣檢驗模型預測的準確性,混淆矩陣見圖7.混淆矩陣的對角線元素為預測正確的樣本量.GBDT模型評估結果見表9,GBDT模型測試數據評估結果見表10.

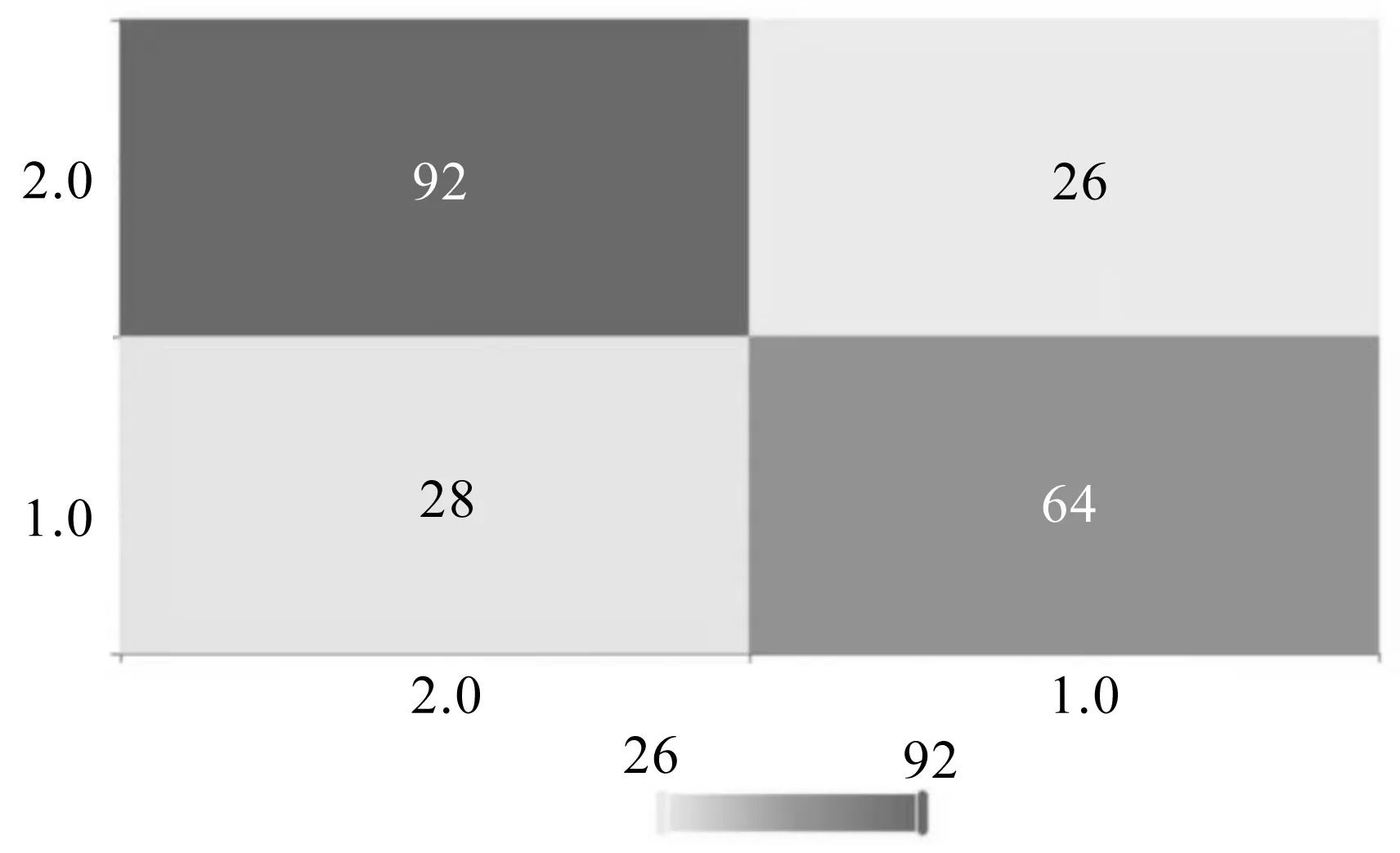
圖7 GBDT模型混淆矩陣圖

表9 GBDT模型評估結果

表10 GBDT模型測試數據評估結果

3.2.3 Adaboost模型與GBDT模型的對比

通過比較adaboost和GBDT兩個模型在訓練集和測試集上的準確率、召回率、精確率和F1,發現adaboost在訓練集上的4項參數數值均低于GBDT,在測試集上的4項參數數值也均低于GBDT.因此,本文選擇GBDT作為構建是否處于信息繭房與系統主導模式和用戶主導模式之間的集成回歸模型.

4 結 論

根據以上模型和預測結果可知,56.67%的浙江高校大學生未受到信息繭房的影響,43.33%的大學生處于信息繭房狀態.這說明浙江省高校大學生在行為和心理指標方面表現良好,具備較高的信息素養水平.這一趨勢可能與浙江省的信息化發展水平和教育水平密切相關.本文采用3種機器學習模型進行信息繭房預測,并對他們進行比較分析.這些模型雖然在預測上表現出色,但預測準確率仍有提升空間.因此,以后的研究應采用多模型融合方法,如stacking異質集成學習,來提高模型的預測準確率,以有助于更準確地預測浙江省高校大學生是否受信息繭房的影響.