富水地層大直徑盾構施工引起的沉降規律分析
李偉
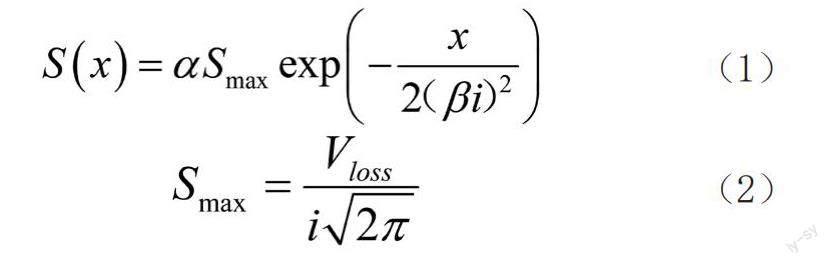


摘要:為了研究富水軟土地層大直徑盾構施工引起的沉降情況,選取杭州地鐵8號線一期工程為研究背景,基于有限差分軟件建立三維數值模型,分析了盾構隧道施工引起的沉降規律。大直徑泥水盾構施工使得地表橫向沉降量不斷增加,且越靠近隧道中心區域地表沉降越嚴重。施工階段的增加也造成了地表縱向沉降的增大,距離施工起始點越遠,沉降變化量越小。地表至拱頂之間的區域,整體沉降量不斷增加,而距離地表越遠、越靠近拱頂區域盾構施工引起的地表沉降變化幅值越大。研究結果表明:大直徑泥水盾構施工會造成施工區域整體富水軟土地層出現不同程度沉降,其中隧道中心、施工起始點和拱頂區域施工引起的地表沉降影響最嚴重。
關鍵詞:富水地層;盾構隧道;有限差分;地表沉降
0? ?引言
近年來,城市地下空間作為城市空間結構的重要組成部分,朝著“網絡化、立體化、集約化、深層化、綜合化”方向發展趨勢更加明顯,人民群眾對城市公共地下空間安全性、舒適性等品質化需求也日益提高[1-2]。
地鐵作為城市軌道交通中最常見的一種形式,通常采用盾構法施工[3]。盾構法施工在一些特殊地質環境建設工程中,尤其在富水軟土地層可達到較好施工效果。但采用盾構機進行施工,所有施工行為都在巖土體內部完成,難免會引起隧道周圍土體的變形與沉降[4],一旦沉降情況超過安全警戒線,便會給帶來不可估量的經濟損失,并可導致人身安全受到威脅。
近年來,相關領域學者針對地表沉降變化進行了大量研究。Peck對隧道開挖引起的地表沉降規律進行了總結,并假定地表沉降曲線符合正態分布,提出了著名的Peck公式。O'Reilly等[5]根據大量工程經驗,認為i和隧道埋深H之間存在簡單的線性關系,即i=kH。文獻[6-7]采用統一土體移動模型,分析隧道施工引起的不同方向的土體變形情況,再結合土體水平位移計算公式,得出施工引起的具體沉降變化值。但是該研究結果不夠精準。
王睿[8]針對目標盾構隧道施工區域,布置多個監測點,分別獲取現場沉降監測數據。結合隧道尺寸、地質條件等多方面影響因素,獲取未來地表沉降預測結果。但該方法的沉降研究時間成本較高。
魏綱[9-10]采用太沙基一維固結理論,得到地面工后固結沉降的理論計算公式。但當隧道埋深較大時,可能產生土拱效應。胡達、馬乾瑛等[11-12]在分析盾構施工引起的土拱效應的前提下,明確施工進程與地表沉降量之間的關聯性。再結合隧道收斂面積、隧道埋深等施工參數,得出地表沉浸計算值。該方法基于彈性假設,簡化了復雜土層的應力應變關系,但未考慮地下水等因素的影響,因此應用存在較大局限性。
基于上述分析,本文以富水軟土地層為研究重點,針對杭州市單洞雙線盾構地鐵隧道施工工程,運用數值模擬分析軟件,模擬大直徑泥水盾構施工過程,研究施工引起的地表沉降變化情況。
1? ?Peck公式修正系數
Peck經驗公式作為預測地表沉降最常用的公式在實際工程中被廣泛運用。然而,該公式是基于早期有限的盾構隧道實測數據而得到的經驗公式,特別是對于復雜地質條件和不同施工方案等因素引起的盾構施工地表沉降,直接用來預測沉降值會存在一定的誤差。
截止目前,大量學者結合不同地區的盾構隧道施工對其適用性進行了修正,即引入地表最大沉降量的修正系數α和沉降槽寬度修正系數β來定義地表沉降曲線的形狀。修正后的Peck公式如下:
式中:x為離隧道中心線的水平距離;Smax為隧道上方沉降最大值;Vloss為施工引起的地層損失;i為沉降槽寬度。
部分學者對這兩個修正系數,通常采用大量工程實測數據進行歸納分析,并通過將修正Peck公式取對數函數的方法,將分散點進行線性擬合找到α和β之間的關系,以此得到修正系數區間的大小,隨后取合適值來預測地表沉降值。
雖然該種方法能夠得到較為準確的預測模型,但在某些情況下缺少適合特定工程的以往實測數據。與此同時,O'Reilly等對沉降槽寬度的取值并沒有考慮到隧道直徑這一因素。為了簡化修正系數的取值,本文通過直接建立沉降槽寬度修正系數β與埋深比之間的關系來確定其大小。計算關系式如下:
式中:n為埋深比系數,H為隧道埋深,D為隧道外徑。由于盾尾注漿的影響,實際地層損失率難以精確計算,對于最大沉降量的修正系數α本文仍然取1。
為了得到n的大小,本文將3個工程案例的實測結果與修正Peck公式進行比對分析,案列一[13]、案列二[14]和案列三[15]的詳情可參考具體文獻,對比結果如圖1所示。當n的取值區間為[0.70,0.80]時,實測結果與Peck修正公式擬合程度較高,因此本文推薦埋深比系數n取0.75較為合適。
2? ?工程概況
本文以杭州地鐵8號線一期工程為研究對象,其施工區域跨越了下沙和大江東兩個經濟開發區,采用大直徑泥水平衡盾構機進行施工,起始和終止里程分別為K2+196.000、K5+702.550,隧道全長為3466.1m,埋深9.5~36.5m,最大坡度26.73‰,最小曲線半徑800m。區間段平面圖如圖2所示。
區間先后下穿錢塘江施工段和北岸海塘施工段,長度分別為2090m和50m,并下穿南岸海塘施工段,長度為30m。區間隧道盾構機開挖直徑為11.7m,管片外徑為11.3m,內徑10.3m,壁厚500mm,每環寬2m。盾構機施工參數如表1所示。隧道斷面地質狀況如圖3所示。
為保證富水軟土地層大直徑泥水盾構施工的順利進行,需在施工區間中部建設一座水泵房,并從施工起點開始共布置14道防護門,相鄰防護門之間的距離小于230m。本區間隧道下穿兩段重點區域,分別是錢塘江北岸下沙段標準海塘、錢塘江南岸蕭圍西線海塘,起止里程分別為DK2+630~DK2+680、DK4+770~DK4+800,區間段各地層的土體參數如表2所示。
3? ?三維數值模型
3.1? ?模型參數
本文采用FLAC 3D有限差分軟件,針對目標盾構施工段建立三維數值模型,如圖4所示。模型長50m,寬32m,高45m,其中模型底部邊界采用固定約束,側面邊界均采用水平法向約束。本文假定如下:土層水平且為各向同性,土體視為理想彈塑性體,服從Mohr-Coulomb屈服準則。管片采用彈性本構模型,管片材料為C55高性能混凝土,混凝土抗滲等級P12,管片視為均質圓環,不考慮橫、縱向螺栓的影響。不考慮開挖面地下水滲流對沉降的影響。
該區段屬于穿江盾構隧道,根據地勘報告取江面水位線高3.5m,各土層參數如表2所示,圖5展示了隧道與地質剖面的關系。
針對大直徑盾構隧道穿越富水軟土地層,施工過程中需要著重考慮水壓力的影響,水壓力矢量如圖6所示。開挖前地層在自重應力下達到平衡,初始地應力如圖7所示。隨后進行位移清零并準備開挖。
3.2? ?測點布置
距離起始開挖面16m處選定15個沉降特征點并進行對稱分布,針對橫向沉降進行監測,測點布置如圖8所示。開挖前后通過A1、B1、C1、D1和E1等5個地表監測點,研究地表縱向沉降。拱頂監測點與之平行,均位于隧道中線平面內,其距初始開挖面的距離分別為4m、8m、16m、20和24m。
4? ?結果分析
4.1? ?橫向沉降
地表橫向沉降值的變化曲線如圖9所示。從圖9可知,隧道中心線處的沉降值最大,隨著水平距離的增加,地表沉降值在不斷減小,曲線基本呈正態分布。隨著開挖面的不斷推進,各測點沉降值遞增,其中位于中心線的測點沉降值從6.9mm逐漸遞增至11.5m。
本文計算結果與Peck經驗公式相比較為接近,但隨著水平距離的增加誤差不斷增大。原因是該經驗公式是基于理想正態分布函數曲線而得到,與實際相比具有一定的誤差。實測沉降對比如圖10所示,從圖10可以看出,修正Peck公式結果與現場實測值相比較為吻合。
4.2? ?縱向沉降
圖11反映了地表沉降值隨不同掘進長度的變化規律。從圖11可以看出,在縱向中心線測點前后4m處的范圍內掘進時,沉降值的增加速度最快,之后緩慢增加。分析認為,開挖面通過測點附近時,地層損失迅速增大,導致地表沉降值的增加,開挖面通過一定距離后對沉降影響較小。
由不同測點間的沉降值對比可知,相同掘進距離下,開挖面先通過的測點沉降值更大。其中,掘進長度大于10m后測點A1的沉降值偏小。這是由于開挖卸載及管片上浮等原因,導致沉降幅度削減。
不同掘進長度下拱頂沉降值的變化曲線如圖12所示。與地表沉降曲線變化規律類似,拱頂沉降同樣在開挖面通過時增長速度最大,在掘進完成后,最大拱頂沉降為15.1mm。相較于地表沉降,拱頂沉降更大,這是因為拱頂沉降直接受到盾尾間隙大小的影響。
5? ?結束語
本文針對富水軟土地層大直徑盾構隧道施工,基于有限差分軟件建立三維數值模型,分析了隧道開挖引起的沉降變化規律,得到如下結論:
隧道埋深比是影響沉降槽寬度修正系數大小的重要因素,建議埋深比系數的取值為0.70~0.80之間。地表橫向沉降槽基本呈正態分布形狀,隨著開挖面的推進,沉降值逐漸遞增;隧道中線處沉降值最大,并隨著水平距離的增加而不斷減小,理論與實測結果較為吻合。地表縱向沉降隨著掘進長度的增加不斷增大,在開挖面通過前后4m的范圍內沉降速度最快,之后沉降緩慢增加。拱頂縱向沉降規律與地表類似,但沉降值更大,最大拱頂沉降為15.1mm。距離開挖起始面越遠,沉降值越低。
參考文獻
[1] 陳湘生.我國城市軌道交通高質量可持續發展的思考[J].城市軌道交通,2023,.87(5):28-31.
[2] 郭鴻.“平戰結合”:人防建設與地下空間的開發與管理[D].南昌:南昌大學,2016.
[3] 申志軍,夏勇.黃土隧道馬蹄形盾構工法選擇及應用[J].隧道建設(中英文),2017,37(12):1518-1528.
[4] 王建秀,付慧仙,朱雁飛,等.基于地層損失的盾構沉降計算方法研究進展[J].地下空間與工程學報,2010,6(1):112-119+150.
[5] O'reilly M P, New B M. Settlements above tunnels in?the United Kingdom: their magnitude and prediction[C] // Proceedings of tunnelling 82. London: Institutionof Mining and Metallrugy, 1982: 17
[6] 魏綱.盾構法隧道統一土體移動模型的建立[J].巖土工程學報,2007,173(4):554-559.
[7] 魏綱,劉加灣.盾構法隧道統一土體移動模型參數取值研究[J].鐵道建筑,2009,420(2):48-51.
[8] 王睿.探析地鐵隧道盾構法施工引起的地表沉降[J].工程機械與維修,2020,291(2):81-83.
[9] 魏綱.盾構施工引起地面長期沉降的理論計算研究[J].巖石力學與工程學報,2008,206(S1):2960-2966.
[10] 張海豐,馬保松,周維.太沙基土拱理論計算隧道受力存在的問題[J].現代隧道技術,2017,54(2):55-60.
[11] 胡達,肖超,梁小強,等.考慮土拱效應的盾構隧道施工地表沉降預測[J/OL].工程地質學報:1-12[2023-09-15].https://doi.org/10.13544/j.cnki.jeg.2022-0561.
[12] 馬乾瑛,業嘉超,蔣小慧.考慮土拱效應的盾構隧道施工地表沉降預測研究[J].現代隧道技術,2021,58(6):148-154.
[13] 廖趙勝,相龍勝,高順宇,等.粉細砂地層雙線盾構施工實測地表沉降規律分析與預測[J]. 土木與環境工程學報(中英文):1-11.
[14] 李宇健,黃戡,孫逸瑋.盾構參數對復合地層損失率和地表沉降的影響[J].交通科學與工程,2022,38(1):70-78.
[15] 陳亦軒,李筱艷,陳松.基于Peck公式的隧道盾構施工引起的地表沉降預測研究[J].安全與環境工程,2023,30(2):79-83+91.

