基于SVR算法的高速鐵路施工全過程造價預測方法

雷保忠

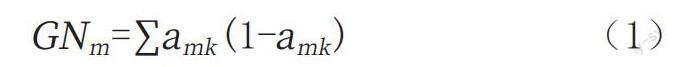
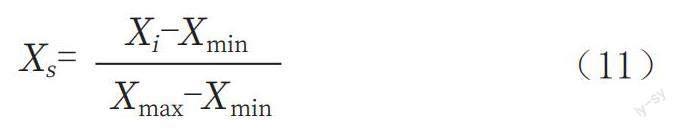
摘要：傳統高速鐵路施工全過程造價預測方法，由于直接選取造價預測評價指標未對影響因素進行分析，造成傳統方法預測偏差率高。針對于此，提出一種基于SVR算法的高速鐵路施工全過程造價預測方法。對高速鐵路施工造價影響因素進行分析，提取影響較大因素的相關數據，并基于SVR算法建立造價預測模型，對高速鐵路項目造價進行預測。設計對比實驗，實驗結果表明：所提出的設計方法預測高速鐵路施工全過程造價偏差率最低，充分證明了所提出設計方法的可行性。

關鍵詞：SVR算法；高速鐵路施工；造價預測；預測方法

0? ?引言

高速鐵路項目是交通運輸的重要解決方案，是具有強周期性和多變量約束的建設項目[1-2]。高速鐵路項目建設階段的造價預測關系到建設的整個生命周期，直接影響項目的實際效益，因此施工單位都對其非常重視。

目前國內很多學者對高速鐵路建設造價預測方法進行了研究，雖然這些研究取得了一定的效果，但仍存在精準度不足等問題。為了解決這些問題，本文提出在SVR算法的基礎上，建立高速鐵路建設全過程的造價預測模型[3]。

使用SVR算法對造價進行分析，可以獲得高速鐵路建設階段最穩定的預測結果。基于SVR算法的高速鐵路工程施工階段造價預測方法降低了預測難度，保證了建設階段造價預測結果的準確性，有效降低了預測方法的偏差率。

1? ?高速鐵路施工造價影響因素分析

不同的造價影響因素都能夠改變預測的準確性。本文采用基尼指數（Gini指數）來評估影響高速鐵路項目造價的因素。基尼指數計算公式如式（1）所示：

GNm=∑amk（1-amk）? ? ? ? ? ? （1）

式中：GNm=為高速鐵路造價影響因素。m為重要性評分。amk為隨機算法中第m個節點的Gini指數。

在節點m前后Gini指數變化量如公式（2）所示：

SimGini=GNm-GNa-GNb? ? ? ? ? ? （2）

式中：SGini為影響因素節點在im上的重要因素，即高速鐵路造價算法中意外分解的m節點雜質的平均變化。GNa和GNb分別為兩個新節點a和b除以m個節點的基尼分量。

如果造價影響系數在j中顯示m次，則造價影響系數顯示在等式中的重要性評價如（3）所示：

SjGini=∑SjGiniGNm? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? （3）

式中：造價影響因素SjGini為造價影響系數在第j次的重要性評分。

隨機算法中影響高速鐵路造價的Gini系數如等式（4）所示：

SiGini=? ?∑SjGini? ? ? ? ? ? ? ?（4）

式中：SiGini為造價影響因素的重要性評估。在算法中n為偶然確定的數量。SGini的值越高，就認為該造價影響因素對于實際工程造價值越重要。

接下來，計算高速鐵路造價影響因素與實際項目造價之間的皮爾遜相關系數，測量兩者之間的線性相關性，并驗證公式（5）中規定的影響因素的產出造價。

式中：為xi和yi之間的皮爾遜相關系數。cov（xi，yi）為xi和yi的協方差，yi為i高速鐵路項目的實際造價，xi為i高速鐵路項目造價的影響因素，[-1，1]的值越接近-1或1，影響因素和造價之間的線性關系就越強。

選取高速鐵路工程各造價影響因素評分排名較高的造價影響因素，以此作為輸入變量代入高速鐵路工程預測模型中，用于進一步計算。

2? ?選取造價預測評價指標

從排名較高的造價影響因素中，提取對高速鐵路施工全過程造成影響較大的因素，完成預測評價指標選取。其中可再生能源市場價格的選取值、施工時間指標的勞動力市場價格與指標的實際值相對應，選取公式如下：

S1=? ?qeB（xi，yi）? ? ? ? ? ? ?（6）

式中：S1為預測的取值用，q為預測的實際值用。e為具體的選取系數。

高速鐵路施工全過程結構的選取公式如公式（7）所示：

S2=1/auc? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（7）

式中：u為整個高速鐵路建設過程中貨物結構的子部分，c為整個高速鐵路建設過程中石灰結構的部分，a為整個高速鐵路施工過程中加強特定結構的比例。

高速鐵路工程中應用的基座包括矩形基座、梯形基座、三角形基座以及重疊基座等，這些基座是用來支撐鐵路軌道和相關結構的基礎，可根據下式來確定選取合適的基座類型：

S3=1/ （m+y+o+z+b）e2? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（8）

式中：b為高軌建設過程中重疊基座的應用比例，o為高軌建設過程中梯形基座的應用比例，y為高速鐵路建設過程中矩形基座的應用比例用，z為整個高速鐵路建設過程中三角形基座的應用比例，m為高速鐵路建設過程中普通基座的應用比例。

高速鐵路工程中常用的材料或構件包括支撐板、水泥分組板和增強管道板等，其選取公式如下：

S4=? ?eknp? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（9）

式中：p為整個高速項目中使用的加固管道的比例，n為整個高速工程中使用的水泥的比例，k為整個高速鐵路中使用支撐流量的比例。

兩個抗震等級和地基處理難度的選取方法也需充分[4]，高速鐵路工程過程的各級抗震等級包括1至4級，選取公式（10）：

S5= ek2? ? ? ? ? ? ? ? ? （10）

式中：k為所有高速鐵路工程過程的抗震等級。

根據上述工程特點，在整個高速鐵路建設過程中，為便于進行造價預測，需要對指標數據進行標準化處理，歸一化公式表示如下：

式中：Xi為高速鐵路建設過程造價預測指數的平均值，X為標準化后獲得的高速鐵路建設全過程造價預測指標值，Xmax為高速鐵路建設過程中造價預測指標的最大值，Xmin為高速鐵路施工全過程造價預計指數的最小值。

3? ?基于SVR算法建立施工全過程造價預測模型

從相關性的角度來看，所有高速鐵路施工全過程造價預測主要分為兩部分：影響因素分析和指標選擇。因此，有必要建立一個造價預測模型，以預測高速鐵路項目的造價。

為減少對造價預測結果的影響因素，通過SVR算法計算得到的高速鐵路工程造價描述如下：

綜合貼近度可以通過結合SVR算法的最大、最小貼近的方法計算，可表示為以下公式：

dH（w，vk）=? V∑∣v-w∣（k=1，2，…，m）? ? （13）

式中：vk為高速鐵路項目v的第k個元素，m為特性元素，dH為待測項目。

總貼近度計算為：

tH（w，vk）=1-dH（w，vk）? ? ? ? ? （14）

當比較各種工程項目的要素集之間的近似值之和的最大值和高速鐵路建設的近似值時，可以獲得測試項目的高速比Bw和高速鐵路施工比vk。

未測量的不確定關系系數為：

在綜合相似性的基礎上，對影響因素的相似性進行排序，高速鐵路項目造價與影響因素的相似度越大，項目造價對影響因素的影響就越大。根據SVR算法計算，高速鐵路工程單元的造價計算如下：

式中：tk1、tk2、tk3為高速鐵路工程因素的綜合相似度。C1、C2和C3為高速鐵路項目的單方面造價[5]。

根據上述公式，對提取的高速鐵路項目造價特征信息進行誤差計算，并再通過SVR算法計算獲得高速鐵路項目的動態數據，得到一個全新依賴關系的高速鐵路工程施工全過程造價預測模型，模型計算如下：

式中：y為高速設計階段的造價預測模型。u（i）為道路項目階段不同信息的造價特征，n為未知x數的重要性，gi為高速鐵路項目造價的影響因素。

4? ?實驗論證

針對本文上述提出的基于SVR算法的高速鐵路施工全過程造價預測方法，為驗證該方法具有較低的預測偏差率，設計如下對比實驗：

4.1? ?實驗準備

實驗選取某高速鐵路施工路段的特定區域，作為實驗對象，收集7個高速鐵路建設案例的資料并進行整理。7個高速鐵路施工長度在1564.26～1869.41km之間。將7個高速鐵路施工全過程作為造價預測實驗樣本，采用本文設計方法和傳統方法Ⅰ、Ⅱ，對7個高速鐵路項目的所有造價進行預測和分析。實驗中的客觀誤差為0.0001，輸入層的初始速率為0.01。

本實驗以高速鐵路工程的全過程造價預測為測試指標，共采用3種方法。根據相關規定，高速鐵路工程造價預測的全過程偏差率不得超過3%，否則預測不具有參考值和預測方法的精度。

4.2? ?實驗對比

利用公式（17）計算本文高速鐵路建設過程的造價，計算的具體結果如表1所示。

根據表1。使用ER軟件計算7個高速鐵路施工過程的造價預測偏差率，并將其作為實驗數據。3種方法造價預測偏差率對比如表2所示。

從表2可知，應用本文設計方法預測高速鐵路施工全過程造價偏差率最低，比傳統方法的造價預測偏差率平均分別低了5.421%和 3.121%，基本與實際情況一致。

實驗結果證明，基于SVR算法的高速鐵路施工全過程造價預測方法具有較低的預測偏差率，在高速鐵路施工全過程造價預測方面具有可行性，預測結果與實際情況基本相符合。

5? ?結束語

傳統高速鐵路施工全過程造價預測方法，由于直接選取造價預測評價指標未對影響因素進行分析，造成傳統方法預測偏差率高。針對于此，本文提出一種基于SVR算法的高速鐵路施工全過程造價預測方法。

先對高速鐵路施工造價影響因素進行分析，提取影響較大因素的相關數據，然后基于SVR算法建立造價預測模型，對高速鐵路項目造價進行預測。

本文研究的預測方法使高速鐵路工程施工全過程造價預測結果的偏差達到最低值，有效降低了預測的困難。采用基于SVR算法建立高速鐵路施工全過程造價預測模型，并進行了合理分析，可降低預測方法的偏差率。

參考文獻

[1] 李謨興，何永秀，柳洋，等.基于大數據的高速鐵路工程造價預測[J].河北電力技術，2023，42（1）：37-44.

[2] 李謨興，何永秀，柳洋，等.基于大數據與機器學習的配電網電纜線路工程造價預測[J].山東電力技術，2023，50（1）：40-46.

[3] 孫勤，李蔚東，肖輝，等.基于模糊貼近度原理的“充砂袋”圍堰造價預測方法應用[J].湖南交通科技，2022，48（4）：178-181.

[4] 袁兆祥，張血琴，郭裕鈞，等.基于Stacking集成模型的電網輸電工程造價預測研究[J].山東電力技術，2022，49（12）：14-19.

[5] 關曉帆.利用模糊聚類算法分析預測輸水線路工程造價[J].黑龍江水利科技，2022，50（8）：158-160.