多角度思考關注數學本質以提升核心素養
——以2023年新高考Ⅱ卷立體幾何為例

吳瑞瑞

(安徽省淮北市第一中學,安徽 淮北 235000)

2023年高考試題突出強調對基礎知識、基本概念的深入理解和靈活掌握,注重考查學科知識的綜合應用能力,落實中國高考評價體系中“四翼”的考查要求,助力“雙減”政策落地.同時,合理控制試題難度,科學引導中學教學,力圖促進高中教學與義務教育階段學習的有效銜接.立體幾何是培養學生邏輯推理、數學運算、直觀想象學科核心素養的一個很好的載體,本文以2023年新高考Ⅱ卷的立體幾何試題為例,從不同角度對解法進行分析,以期為老師的教學,學生的學習提供可借鑒的方法和思路.

1 試題再現

題目(2023年新高考Ⅱ卷第20題)如圖1,三棱錐A-BCD中,DA=DB=DC,BD⊥CD,∠ADB=∠ADC=60°,E是BC的中點.

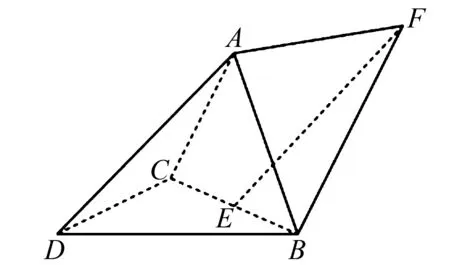
圖1 2023年新高考Ⅱ卷第20題

證明:(1)BC⊥DA;

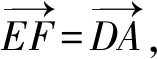
2 試題解析

分析第(1)問要證明的是異面直線垂直,常用到的方法是證明線面垂直以達到證明線線垂直的目的,或把異面直線問題轉化為共面直線問題,體現降維思想.再利用三角形的有關知識解決,或者利用基底法證明向量數量積為0,也可以選擇特殊的基底,比如常用到的坐標法也就是選擇單位正交基底來進行解決.

第(2)問求二面角的正弦值,可以采用傳統幾何法找到二面角,然后解三角形;也可以采用向量法,利用選擇的基底表示面的法向量;也可采用坐標法(特殊的基底),找面的法向量或者是找到垂直于交線的兩個向量,進而求出二面角的正弦值[1].

2.1 第(1)問解析

解法1如圖2,連接DE,AE,因為DB=DC,所以DE⊥BC.又由DA=DB=DC,∠ADB=∠ADC=60°知,△ADC≌△ADB或△ADC,△ADB為等邊三角形.因此AB=AC.故AE⊥BC.又AE∩DE=E,所以BC⊥面ADE.又DA?面ADE,所以BC⊥DA.

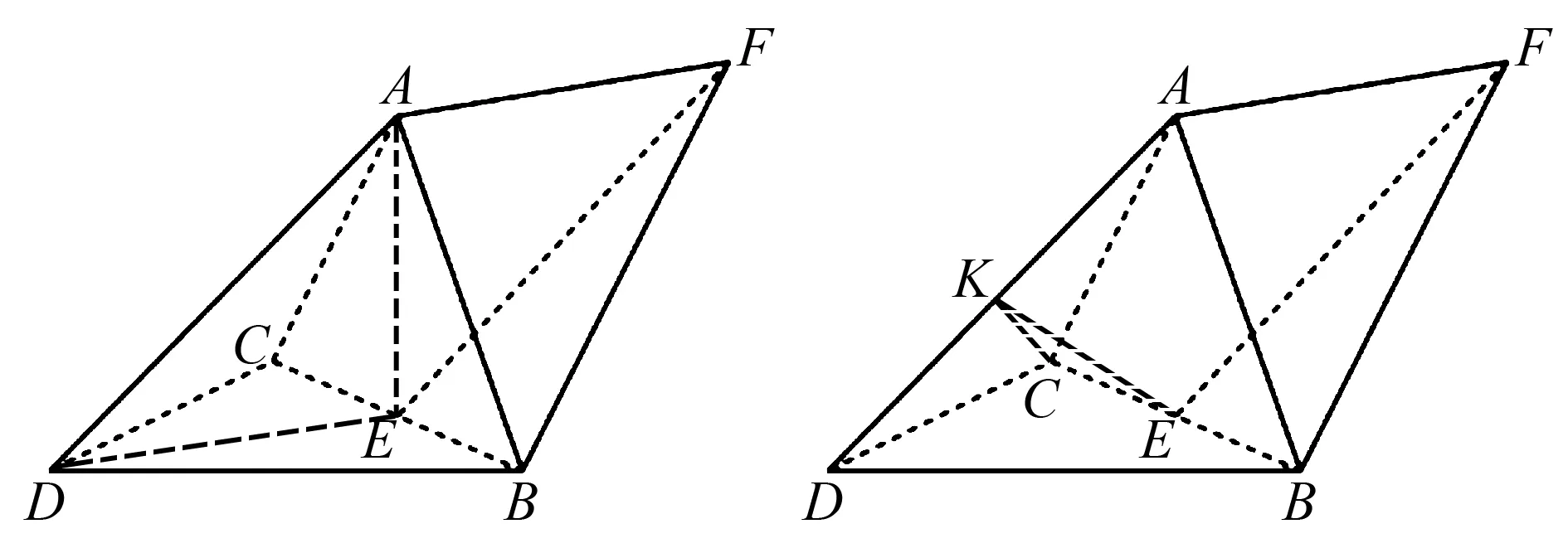
圖2 第(1)問解法1示意圖 圖3 第(1)問解法2示意圖

解法2如圖3,取DA的中點記為K,連接BK,CK,由題知△ADC,△ADB為等邊三角形.故DA⊥BK,DA⊥CK.又BK∩CK=K,所以DA⊥面BCK.

又BC?面BCK,從而BC⊥DA.

解法3如圖4,分別取AC,DC,DB的中點M,N,J,連接MN,MJ,NJ,則要證明BC⊥DA,只需要證明MN⊥NJ.

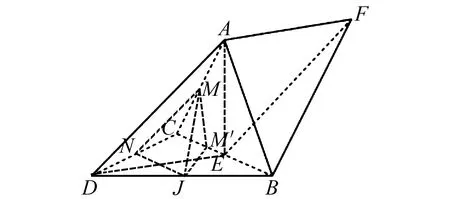
圖4 第(1)問解法3示意圖

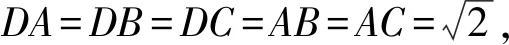
又AE⊥BC,所以AE⊥面BCD.

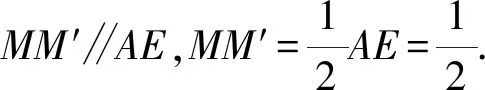
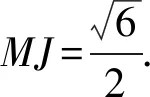
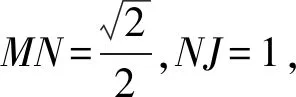
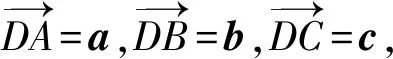
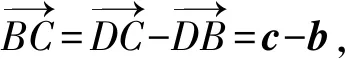
所以BC⊥DA.

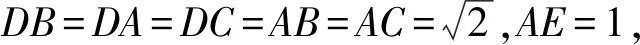
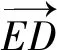
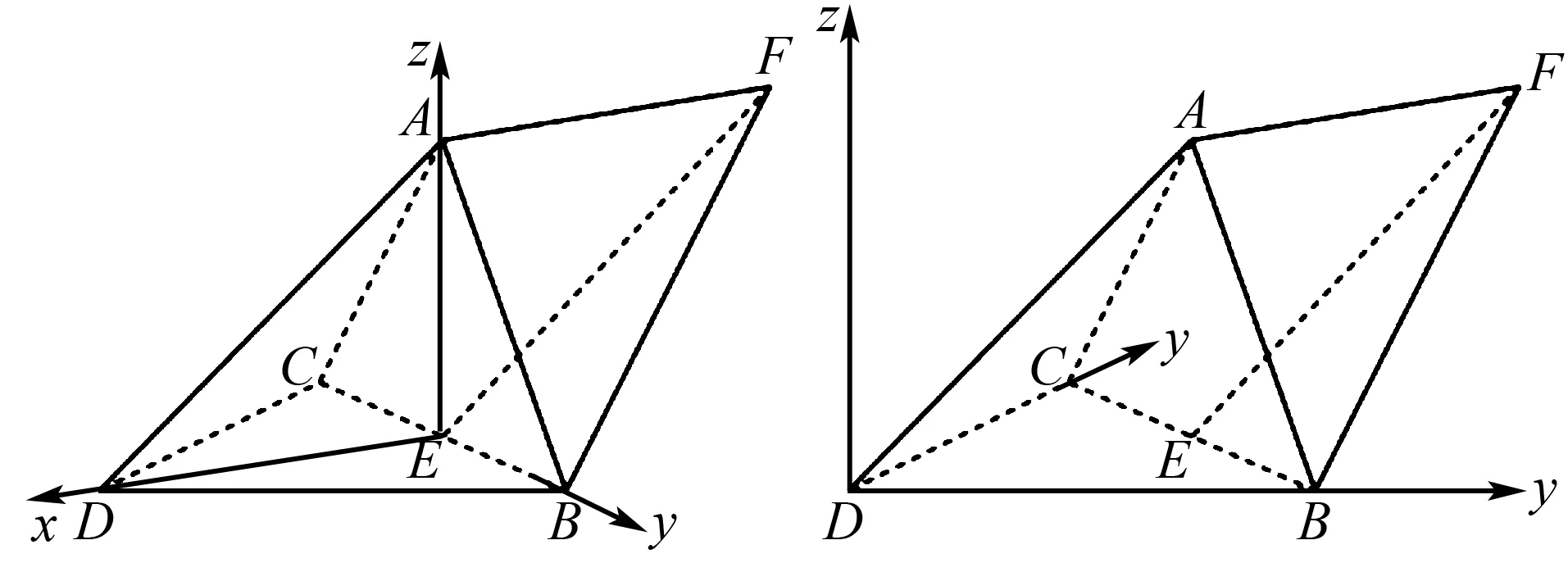
圖5 第(1)問解法5示意圖 圖6 第(1)問解法6示意圖

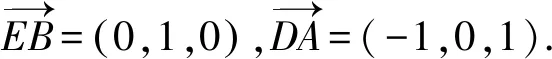
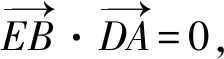
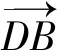
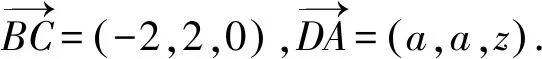
2.2 第(2)問解析

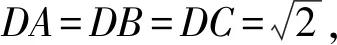
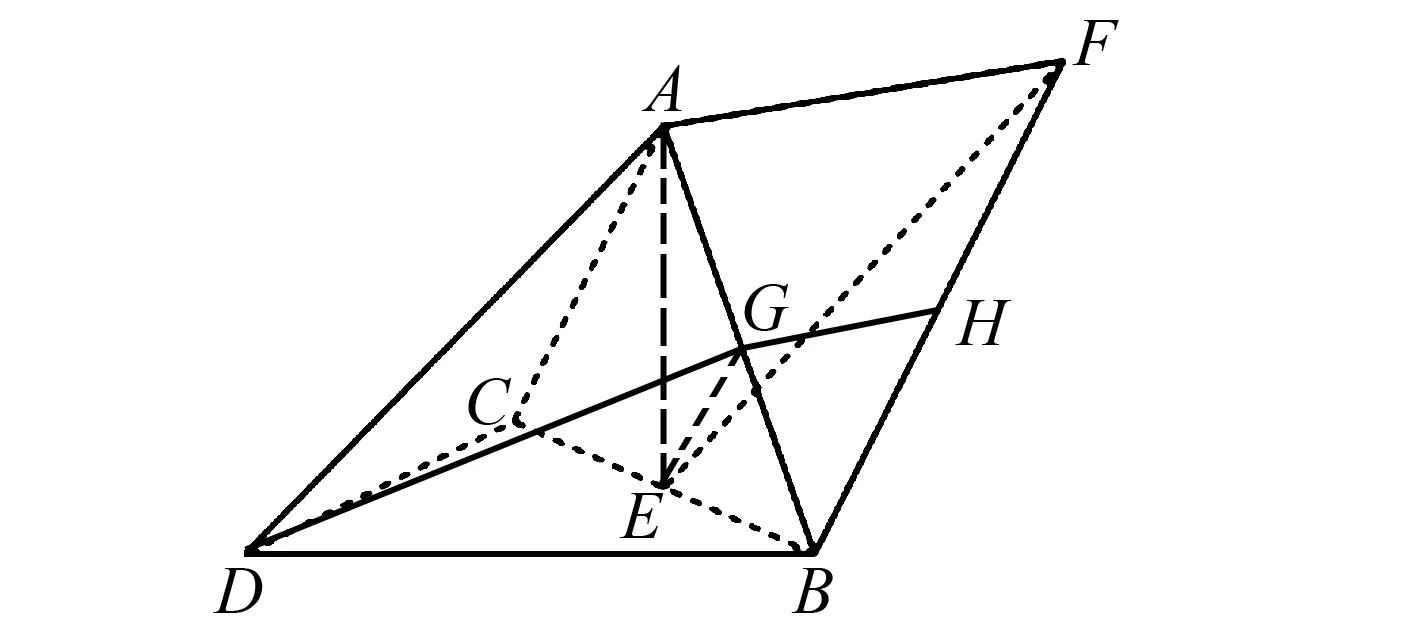
圖7 第(2)問解法1示意圖

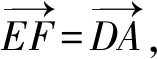
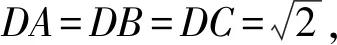
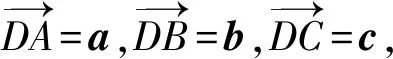
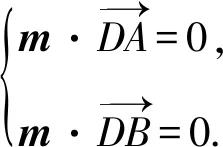
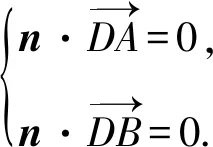
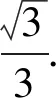
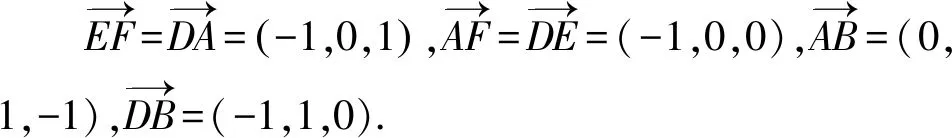
不少老師發聲說,新教材更加重視空間向量,而且對于線面角、面面角的問題,學生幾乎全部選擇建系處理,那么傳統幾何法和向量法更應側重哪一個?章建躍主編曾給予回復說,無論是向量法還是幾何法,我們都要用幾何眼光去觀察圖形,然后才是用向量法解決,對象還是幾何對象,需要了解幾何對象結構的基本關系,如果不了解幾何對象,是無法運用向量法的,如果不熟悉空間結構就無法建系.也就是說對于立體幾何問題的解決,先是直觀想象和邏輯推理能力的考查,再選用向量這個有利工具去程序化地解決問題.