借助圖式辨析，促進概念融通

吳夢媛

【摘? ?要】“倍”用于描述兩個量的比較關系，和乘除法有密切聯系，對學生后續學習分數、百分數和比有重要的作用。理解“倍”的概念，圖式是直觀形象的學習材料。教師可借助圖式設置任務，以任務驅動的方式引導學生對點狀的知識進行補充、完善，促進學生深度理解“倍”的概念。

【關鍵詞】單元復習；圖式辨析；多元表征

單元復習課既要整理、回顧單元知識，關聯數學概念，使學生形成知識結構，又要通過練習查漏補缺，使學生完善認知結構。然而，“理”容易枯燥，“練”容易細碎。如何讓數學概念的復習既不枯燥又整體關聯呢？筆者以人教版教材三年級上冊“倍的認識”的單元復習為例，借助圖式設置任務，進行復習教學的嘗試。

一、解讀概念，明晰單元核心內容

以復習數學概念為主的單元復習課一般包括兩個層面：一是理解數學概念的內涵本質，二是明晰數學概念的外延關聯。“倍”是一種比較關系，與乘除法概念有關聯，“倍”的概念直接關聯后續學習的“分數”“百分數”“比”等知識。

人教版教材把“倍的認識”作為獨立的教學單元進行編排，其意圖是讓學生在理解“倍”的概念后，運用“倍”的關系解決問題，主要包括“求一個數是另一個數的幾倍”和“求一個數的幾倍是多少”兩種情況。此外，教材還在期末“總復習”中，以圖式填空的形式，補充了逆向的“已知一個數的幾倍，求這個數是多少”的解決問題。筆者查閱了其他不同版本的教材，發現這些教材也同樣凸顯了“倍”與乘除法之間的關系，體現了“兩個量的倍比”與“兩個量相差”的區別。

因此，“倍的認識”單元復習的核心內容，應是深入理解“倍”的概念，凸顯基于乘除法概念的比較關系，明晰量與量之間的聯系。復習路徑為：借助幾何直觀，抽象概念，把“兩個量數的抽象關系”轉化為“兩個量圖的具象關系”。由此，讓學生明晰倍數的三個量之間的內部聯系，辨析相差關系，延伸包含的倍比關系。

二、分析學情，找準單元知識難點

單元復習課的任務要針對學生的易錯點和單元知識的難點設置。學生在學習“倍的認識”單元時，哪些題目容易出現錯誤？這個單元知識的難點在哪里？針對這些問題，筆者設置了前置式任務，調研了不同班級共247名同學，并對學生的解答情況進行了分析統計。

此次調研中，第一題主要考查學生能否準確描述兩個量之間的倍數關系，第二題考查學生能否根據倍數關系準確畫出“標準量”和“比較量”，第三題考查學生能否在比較多個量時，排除多余信息，準確寫出兩個量的倍數關系。調研結果顯示，第一題約有87.04%的學生能準確描述兩個量之間的倍數關系；第二題第1小題約有87.04%的學生能用圖式表示倍數關系，第2小題約有70.04%的學生能用圖式表示倍數關系；第三題約有76.92%的學生能正確描述倍數關系。此外，此次前置式任務調研也發現了學生存在的一些典型錯誤（如圖1）。

根據學生的具體解答可以發現，在學完“倍的認識”單元后，學生仍然存在以下問題：（1）對于“倍”的概念的理解不夠深入，容易混淆“標準量”和“比較量”；（2）簡單認為圖式中一共有幾份，兩個量就是幾倍關系；（3）存在見“倍”就“乘”的現象；（4）遇到多個量比較時，難以判斷以誰為“標準量”。

三、圖式辨析，遞推單元核心任務

建立關聯是單元復習課的目標之一。基于任務驅動的復習，要把零碎的知識點整合在核心任務中，以圖式的形式組建系列任務，改變“提問—回答”的單一互動模式。

（一）再現：借思辨性圖式，理解概念本質

在單元復習教學中，教師要借助適切的學習材料，幫助學生再現單元內知識點，梳理知識結構，避免抽象枯燥的重復回顧。用于再現知識的任務情境要能涵蓋全單元相關知識，突出教學重難點，幫助學生逐步抽象理解概念本質。

任務一是一組思辨性的圖式（如圖2），借助該圖式能幫助學生進一步理解“倍”的概念。其中，①號圖根據學生的易錯點區分“標準量”；②號圖通過隨意擺放，讓學生聚焦圖形數量，以數量關系理解“倍”的概念；③號圖具有思維遞進關系，需要學生借助規律得出結論；④號圖用線段圖來表征“倍”的概念。

學生先獨立思考完成任務，然后進行教學反饋。教學反饋時，先反饋正確的圖式，概括概念的共性，再辨析錯誤的圖式，強調“標準量”和“比較量”的關系。

“哪些圖能表示圓的個數是三角形個數的3倍？”教師先以正確的②號圖為例，引導學生回顧“倍”的概念，讓學生通過圈一圈、畫一畫，得出：2個三角形為1份，圓有這樣的3份，就可以說圓的個數是三角形個數的3倍。

教師提問：“③號圖后面的珠子被盒子擋住了，你是怎么看出圓的個數是三角形個數的3倍的？”啟發學生在思辨中理解“△○○○”為一組重復出現的圖形，只要觀察其中一組就可以推測出倍數關系。

教師追問：“④號圖只有兩條線段，沒有對應的數量，為什么也能表示‘圓的個數是三角形個數的3倍？”引導學生思考：如果三角形表示1，圓有幾個？如果三角形有2個、3個、5個……[a]個，圓分別是幾個呢？從而滲透函數思想：雖然不知道三角形和圓分別有幾個，但圓的個數始終是三角形個數的3倍。比較歸納“倍”概念的本質：正確表示的這三幅圖，有什么相同點？

在此基礎上，教師提出質疑：“①號圖中有9個和3個，為什么不能表示圓的個數是三角形個數的3倍？怎樣改就可以了呢？”從而讓學生感悟到要找對標準量。由此可知，教學反饋的重點是通過思辨感悟“倍”的概念，從“關注具體數量”走向“關注兩個量的關系”。

思辨性圖式材料可以幫助學生梳理單元知識，形象化地突破難點，抽象出數學模型。單元復習教學如果用思辨性圖式導入，起點較低，學生就會有話可講。在學生分析圖式的過程中，教師要關注學生的語言表述，引導學生先分析標準量，再分析兩個量的倍數關系。數學概念的學習過程就是先將具體情境抽象成數學模型，再用自己的語言描述數學模型的過程。在單元復習課中再現知識，有助于學生內化知識，形成自己的認知結構。

（二）關聯：借對比性圖式，構建知識結構

單元復習教學要關注相似概念的比較，讓學生理得清、道得明、悟得透。“倍”與之前學習的“誰比誰多”的數學問題都是用于描述兩個量的關系，但“倍”的本質是乘除法結構。借助對比性圖式進行復習，可以讓學生明晰不同關系的聯系和區別。

如圖3所示，這是一組對比性圖式，用于幫助學生理解“倍”的比較關系。教師呈現圖式后，讓學生自主列式，然后通過四幅圖的兩次分類，遞進式地展開教學反饋。第一次分類聚焦比較關系。教師提問：“①號圖、②號圖和④號圖都是用乘法或除法表示，③號圖為什么是用減法呢？”學生發現，③號圖雖然呈現的也是兩個量之間的比較關系，但卻是“求一個量比另一個量多幾”的相差關系，而“倍”是描述乘法的數學模型。第二次分類聚焦“倍”的三個量之間的關系。①號圖、②號圖、④號圖分別對應“求幾倍數”“求倍數”和“求一倍數”，從而完善學生對“倍”的理解，幫助學生構建完整的知識結構。

在上述比較的基礎上，教師刪去表示相差關系的題目，只留下表示倍數關系的三道題目，并提問：“同樣是表示倍數關系的三道題，為什么有的用乘法計算，有的卻用除法計算呢？”學生比較三道題的對應圖式，發現“求幾倍數”用乘法，“求倍數”和“一倍數”用除法。接著教師進一步引導學生用“幾個幾”的乘除法模型進行理解，如④號圖是把27平均分成3份，求1份是多少，這“1份數”就是“標準量”，用除法解決。

將對比性圖式進行比較，有助于學生以“類”的思想統領概念，促進對概念的理解和遷移。因此，單元復習教學要將新舊知識進行關聯，梳理知識脈絡，且這種梳理不僅僅是知識的再現，還要在知識再現的基礎上進行關聯與拓展。

（三）進階：借綜合性圖式，促進思維提升

單元復習教學不僅要明晰概念的內涵，還要辨析概念的外延。借助綜合性圖式關聯后續知識，可以延伸知識，促進思維的進階。

1.選擇包含關系的圖式，延伸后續知識

“倍”是描述“率”和“比”的基礎。如“甲是乙的2倍”還可以說成“乙是甲的[1/2]”“甲和乙的比是2∶1”“乙是甲的50%”等。人教版教材在“倍的認識”這一單元研究的均是兩個獨立量之間的倍數關系。但實際上，存在包含關系的兩個量之間也存在倍數關系，比較常見的是在扇形統計圖中用百分數描述倍數關系。

任務三是一組包含性圖式（如圖4）。教師出示任務三，意圖通過變式，幫助學生理解“倍”的比較關系。

教師提問：“你能在圖中找到哪些倍數關系？”針對這樣的開放性問題，學生會有不同的說法，如“桃樹的棵數是梨樹棵數的3倍”“男生人數是女生人數的1倍”“女生人數是男生人數的1倍”等。也有一些學生會關注部分與整體的關系，感受到圖式的包含關系，發現“果樹的總棵數是梨樹的4倍，全班人數是女（男）生人數的2倍”。于是教師進一步追問：“反過來，女生人數是全班人數的多少？”學生會想到“一半”或“[1/2]”。這種“一半”或“[1/2]”的表達，表示學生對標準量的理解更進一步，突破了整數倍，為后續學習“一個數是另一個數的幾分之幾”做了鋪墊。

2.遞進多個量比較的圖式，綜合運用知識

利用開放性的素材，設計綜合性和挑戰性的任務，可以提升單元復習教學的拓展性，具體可以采用條件的開放、問題的開放和方法的開放等方式。

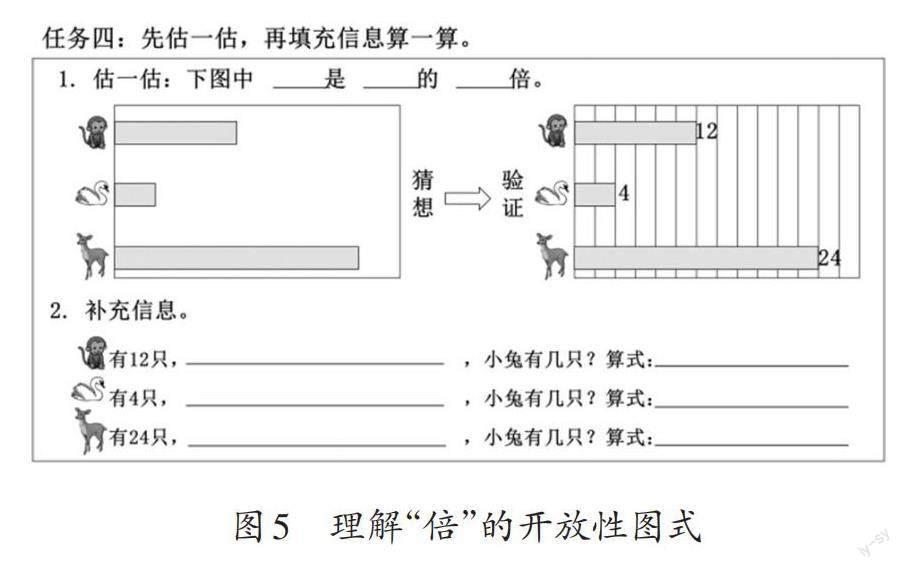
任務四是一組開放性的圖式（如圖5），學習材料從兩個量的比較過渡到多個量的比較。教師出示任務四，旨在培養學生解決問題的綜合能力。

首先，結合條形的長短猜想倍數關系體現了問題的開放。教師提問：“請你估一估，小猴、天鵝、小鹿的只數可能存在哪些倍數關系？”在此基礎上呈現網格和具體數據，引導學生驗證猜想，關注多個量的比較，判斷標準量，用“誰是誰的幾倍”進行描述。其次，條件和解題方法也具有開放性。教師可以引導學生思考：小兔也來湊熱鬧了，請在橫線上補充跟小兔只數有關的信息，并列式計算小兔的只數。這樣的學習任務充分激發了學生的學習興趣，學生既有補充相差關系的，如“小兔比小猴多（少）2只”“小猴比小兔多（少）2只”等，也有補充倍數關系的，如“小兔的只數是天鵝只數的2倍”“小猴的只數是小兔只數的2倍”等。不同學生采用不同的數量關系和表述方式，補充的數據和解題的方法也有不同。他們在這些眾多的表達中，發展了綜合運用知識的能力。

學習的過程是知識不斷同化和順應的過程，而圖式是同化和順應過程中的重要工具。借助圖式設置單元復習課的核心任務，有助于核心任務的整體呈現，契合學生的認知特征，能體現解題的過程化和思維的可視化，從而促進學生對概念的理解和認知結構的建構。

參考文獻：

［1］方舒云.互助式單元復習課的教學實踐與思考：以“倍的認識”單元復習教學為例［J］.小學數學教育，2022（23）：23-26.

［2］張優幼.以實證分析促進概念的深度理解：“有余數的除法”的教學重構［J］.教學月刊·小學版（數學），2023（5）：55-59.

［3］徐曙華.借圖促思? ?深度學習：以“倍的認識”單元整理與復習課為例［J］.教育界，2022（22）：2-4.

（浙江省臺州市學院路小學）