基于響應面法的液壓機械臂結構優化

孫 凱

南京市特種設備安全監督檢驗研究院 南京 210019

0 引言

在半個世紀前，計算機技術的發展給結構優化設計帶來新的發展契機，涌現出大量的工程優化設計算法和軟件[1]。高效的機械結構優化流程的實施離不開基礎理論、力學分析手段和軟件方法實現，這些基礎學科的發展為工程設計者提供了清晰的設計思路和工具。目前，針對機械結構的優化設計主要分為尺寸優化、形貌優化、拓撲優化等，優化設計理論比較完備，且在各領域均有廣泛應用案例，如Ansys、Nastran和Hyperworks等CAE分析軟件中均已加入優化分析功能模塊[2]。

近年來，國內外學者已將結構優化設計理論應用到機械臂設計中。Rout B K等[3]以平面機械手和四自由度機械臂為研究對象，以尺寸和質量為優化目標開展機械臂的優化設計，將對運行精度和重復定位精度的影響降到最小；Hedge G S等[4]采用拓撲優化技術對機械臂進行結構優化設計，以柔度、質量降低為優化設計的目標，將彈性位移、速度作為約束條件，實現了初步的優化目標；Zhou L L等[5]以機械臂的動力學性能為約束條件，利用有限元分析技術進行動應力計算，系統全面地考慮了傳動鏈、零件尺寸等因素，對五自由度機械臂結構開展了以減重為目標的輕量化研究；羅忠等[6]針對細長機械臂結構優化問題，提出了一種基于剛度靈敏度分析的參數優化方法；管貽生等[7]將動力學分析與有限元分析相結合，基于動力學仿真尋找到最危險的機械臂姿態，對工業機械臂進行尺寸優化和拓撲優化，取得了良好優化效果；劉延杰等[8]以機械臂各臂的制造板材厚度為優化設計變量，提出了以柔性關節結構模態頻率為目標的優化設計新方法，為了避免結構柔度過小，在優化過程中還增加了靜態偏移量為約束條件；任亮等[9]利用靈敏度分析技術篩選優化設計參數，大大降低了待優化參數規模，并在此基礎上對六自由度機械臂進行參數優化，同時達到了增大機械臂的模態頻率、改善力學性能和輕量化等多個目標。

機械臂的結構優化設計以結構疲勞壽命、動柔度、經濟性、可制造性等指標為約束條件，通過對機械臂的結構尺寸、形狀、拓撲構型、材料、工藝等方面進行合理調整，使指定的性能指標達到最優（如質量最輕、能耗最小等）[10，11]。如圖1所示，船用起重液壓機械臂的主要功能是離岸吊裝（如將船上的重物，通過起重機械臂運輸到碼頭地面）一些重要精密設備對起吊過程中的沖擊振動、平穩性要求尤為嚴格，需要對機械臂進行精密主動控制。機械臂自身的質量直接影響控制系統的響應速度，故起重機械臂的輕量化設計是重中之重。

圖1 船用起重液壓機械臂示意圖

本文以圖1中船用液壓機械臂的實驗室樣機（相似縮比模型）為研究對象，進行剛柔耦合動力學建模，計算其在典型、完整工作循環中的各關節載荷時域響應。以機械臂結構輕量化設計為優化目標，以機械臂主承力構件—主臂板材厚度為待優化參數，以主臂最大米塞斯應力為約束邊界，建立待優化參數與約束邊界之間的多項式響應面模型；采用蒙特卡洛法在約束邊界內進行全局尋優，得到機械臂輕量化設計結果；再將優化后的結構參數帶入有限元模型中，驗證優化結果的正確性。

1 基于多項式響應面法的優化設計理論

響應面法的基本核心是采用多項式或其他方法（如支持向量機函數、神經網絡等）建立可以模擬實際系統輸入輸出關系的數學模型，避免求解規模巨大的有限元、多體模型，在提高分析效率的同時保證符合要求的精度。其中，多項式擬合法因其構造簡單、物理意義明確，在工程實踐中使用最廣泛。多項式法線性擬合多元自變量與因變量的關系式為

式中：X1、X2、…、Xm為m個一般自變量，Y為因變量，β0、β1、…、βm為未知的回歸系數，ε為隨機誤差。

為了計算回歸系數，需要對X1、X2、…、Xm做n次測量，得到n組測量數據（Yi、Xi1、Xi2、…、Xim），i＝1、…、n，n＞m，則回歸關系為

多項式響應面中的二階多項式方法在工程應用中較普遍，其形式可表示為

式中：y（x）為系統的響應，可以為加速度信號值、應變值、模態特征值等；x＝（x1，x2，…，xm）為響應面中的樣本點，即試驗設計點；m為試驗參數數量；β為回歸系數。

結構優化設計的目的是在滿足結構功能要求的前提下獲得最優的解決方案，如尺寸最小、質量最輕，其流程主要包括定義目標響應和待優化參數、定義邊界約束、優化計算等。

2 機械臂剛柔耦合動力學建模及分析

在機械臂結構優化設計中，需將結構最危險工況下的載荷作為邊界條件輸入到力學模型中。傳統的篩選典型靜力學工況的分析方法由于忽略了系統加減速過程、振動沖擊等因素，且人工考慮極限工況可能會有遺漏，不能反映機械臂真實工作受力情況。為了計算液壓機械臂在工作過程中各關節點的真實動態載荷用于后續結構優化的載荷輸入條件，需進行剛柔耦合動力學分析。

在多體動力學軟件MSC.ADAMS中，建立機械臂的剛體模型，并進行運動學仿真，評估模型的機構運動特性是否符合設計要求。再將有限元軟件生成的包含機械臂主臂、伸縮臂網格信息、模態結果信息等的.mnf文件導入MSC.ADAMS軟件中，并建立機械臂剛柔耦合動力學模型。剛柔耦合模型既可模擬機構運動學，又可同時研究柔性體的彈性位移、應變等力學響應。

模擬機械臂在真實工作狀態將貨物從船上運輸到地面等各起吊工況下的動力學特性，同時進行主臂關節節點力計算。主臂關節動態載荷即為主臂結構優化載荷輸入條件。機械臂剛柔耦合動力學模型及將貨物從船上運輸到地面時各關節節點的載荷如圖2所示。

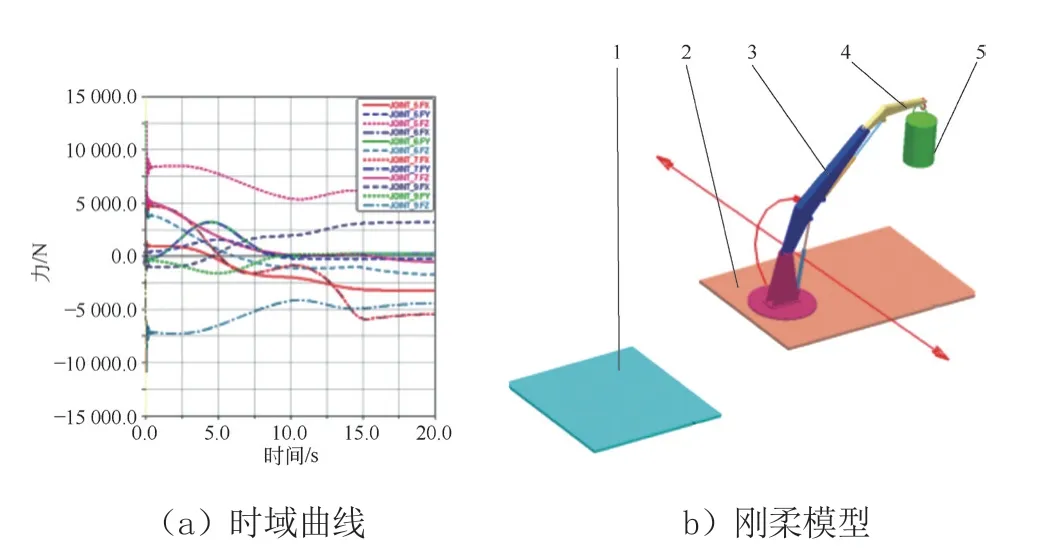
圖2 機械臂剛柔耦合模型及關節載荷

在圖2b中，液壓機械臂的剛柔耦合模型將一個圓柱體重物負載從船舶平臺運輸到另外碼頭岸上，此為一個作業循環。機械臂的主臂和伸縮臂各具有前后2個關節，每個關節的受力沿X、Y、Z方向進行分解，共計12個分量，如圖2a所示。在剛柔耦合動力學模型中，液壓機械臂將貨物從船上運輸到地面的過程中4個典型時刻（即起吊開始、提升階段、平移運送負載、釋放負載等時刻）的機械臂米塞斯應力云圖如圖3所示。

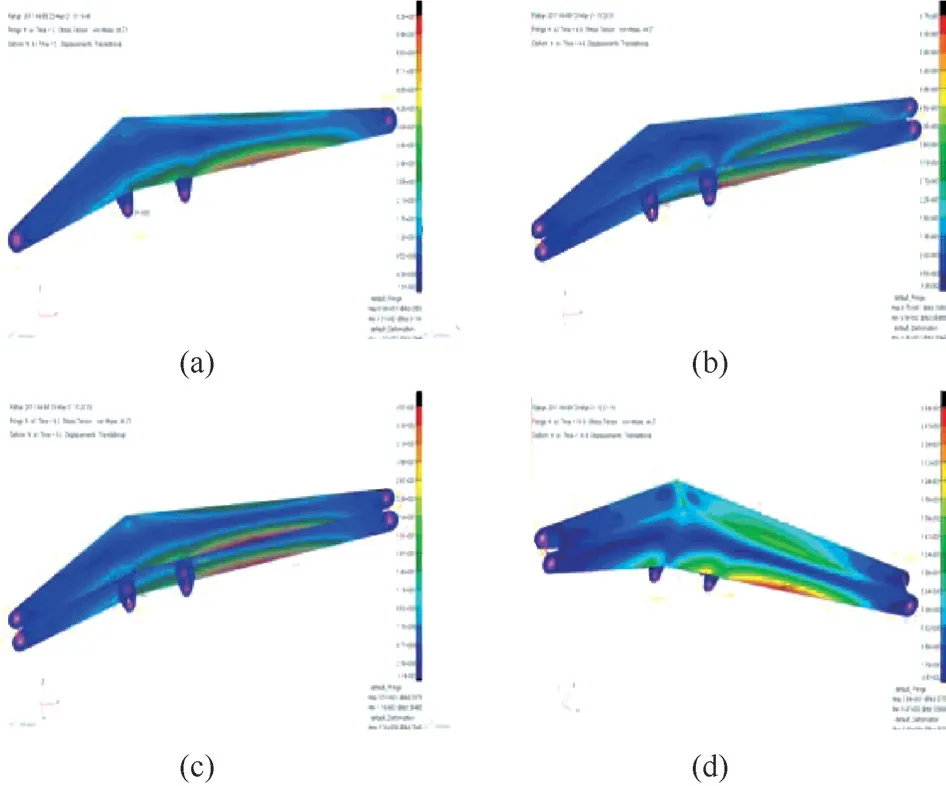
圖3 4個時刻主臂米塞斯應力云圖

由圖3可知，主臂米塞斯應力較大的部位在其內側受壓處，且受力較均勻，應力集中情況較少。保證應力云圖中每一點都符合安全系數要求是輕量化過程中的約束條件，主臂總質量只需用其板材厚度和密度經過簡單代數運算即可求出，而主臂板材厚度與主臂最大米塞斯應力之間無顯式的數學關系表達式，需要采用響應面模型進行描述。

3 基于響應面法的機械臂結構優化

3.1 試驗設計

試驗設計是關于怎樣合理安排試驗的數學方法，其確定了設計點的數量及分布規律，是建立高精度響應面的首要步驟。常用的試驗設計方法包括全因子、均勻試驗設計、正交試驗設計等。拉丁超立方抽樣（Latin Hypercube Sampling，LHS）是一種分層的隨機抽樣方法，可改進抽樣策略，使產生的隨機數更具代表性。LHS抽樣能以較少采樣次數獲得較高的采樣精度，其采樣點均勻分布于設計區間內，而非集中在中值區域。如圖4所示，將主臂按加工過程中的板材結構分布進行材料劃分。

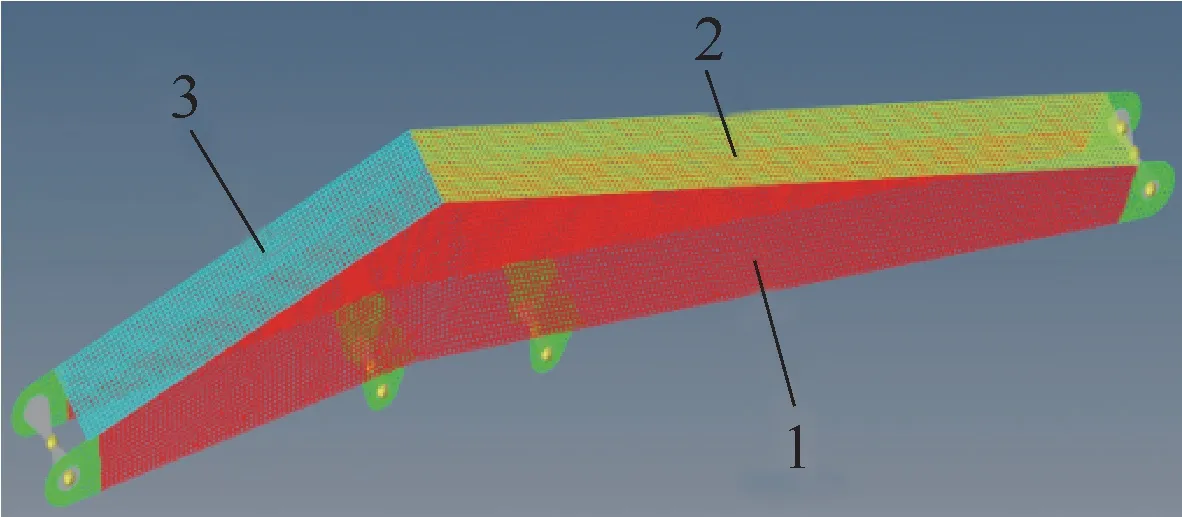
圖4 參數分區示意圖

在圖4中，1、2、3為在機械臂制造過程中的鋼板分區，每個分區由一整塊金屬板材焊接而成，每個分區采用同一厚度規格的板材，選取板材厚度為待優化參數。采用LHS方法對主臂區域Ⅰ、區域Ⅱ、區域Ⅲ（對應的板材厚度參數為P1、P2、P3）進行抽樣，綜合考慮建模速度和精度，抽樣點數為100個，參數P1、P2、P3的初始值為10 mm。根據工程經驗，抽樣上下邊界均為參數初始值的50%～150%。

3.2 多項式響應面建立

建立響應面模型可以模擬原始有限元模型的輸入輸出關系。在結構優化迭代過程中，只需在響應面模型中進行擬合計算，即可避免反復調用耗時較長的有限元求解器。此外，該方法同時具有數據精度高、計算速度快等優點。將100個試驗設計點分別輸入有限元模型中，計算出100個對應的主臂最大米塞斯應力。通過嘗試，選用5階多項式方法擬合樣本點，建立3個設計參數（P1、P2、P3）和主臂最大米塞斯應力之間的響應面模型，其中區域Ⅰ、區域Ⅱ的板材厚度與最大應力之間的響應面模型如圖5所示。

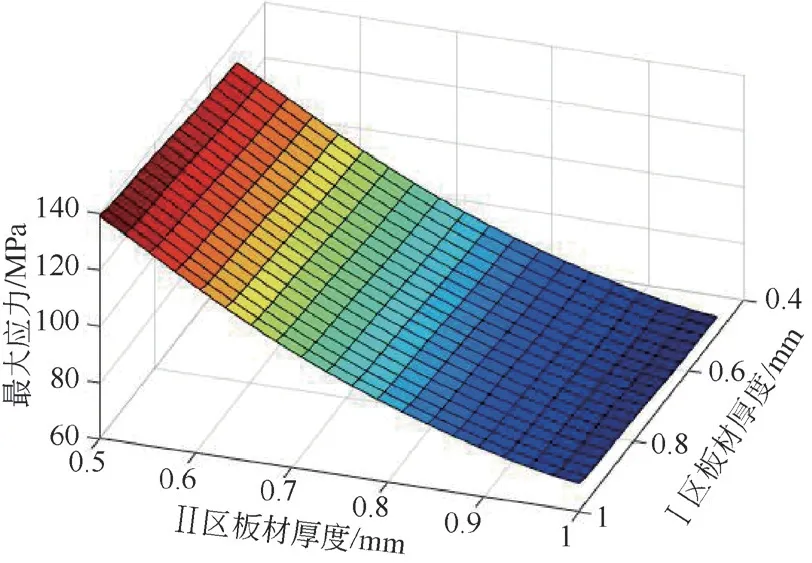
圖5 區域Ⅰ、區域Ⅱ響應面模型

在圖5中，橫縱坐標表示當區域Ⅰ、區域Ⅱ板材厚度從0.5 mm變化到1.0 mm時，豎坐標表示主臂最大米塞斯應力從62.0 MPa變化到145.0 MPa。

在實際工程問題中，響應面模型的精度和泛化能力必須滿足一定的要求，故所建立的響應面模型都要按照一定的指標進行精度評價。本文通過常用的均方根誤差(RMSE)及決定系數R2這2種標準對響應面模型精度進行評估。其表達式為

式中：y、ys為設計空間中各樣本點對應的試驗真值和代理模型預測值；為設計空間上各點的均值；RMSE為設計空間各點試驗真值和代理模型預測值之間誤差占平均幅值的百分比；R2為決定系數，即試驗真值與代理模型預測值之間的總體差異程度，取0～1。

如果R2越接近1、RMSE越接近0，則代理模型越能反映真實的參數和響應之間的關系。通過對響應面進行檢驗，決定系數R2均大于0.99，相對均方根誤差RMSE均小于0.001，響應面模型精度滿足工程要求。

3.3 基于蒙特卡洛法的響應面尋優

采用蒙特卡洛法求解響應面最優問題既可避免求解過程陷入局部最優，也可兼顧較高的求解效率。在設計參數的取值空間內，再次采用拉丁超立方抽取2萬個樣本點。由于LHS為分層均勻抽樣，2萬個樣本點從概率學上能完全覆蓋3個參數的取值空間。

將2萬個樣本點帶入響應面模型中，計算主臂在嚴苛工況工作下的最大米塞斯應力。結果顯示，米塞斯應力為62.0～145.0 MPa。機械臂采用LY12材料制造，其屈服強度為325.0 MPa。在實際工程中，結構取4倍安全系數，即材料許用應力為81.25 MPa。在圖6中，區域Ⅰ、區域Ⅱ、區域Ⅲ板材厚度為一個參數取值的組合，如區域Ⅰ、區域Ⅱ、區域Ⅲ的板材厚度取6.5 mm、8.2 mm、9.8 mm時為一個滿足許用應力要求的參數組合，即一個樣本點。圖6為從2萬個樣本點中篩選出的3 799個滿足材料許用應力要求的樣本點。計算3 799個樣本點對應的主臂質量，最小質量為74.5 kg，區域Ⅰ、區域Ⅱ、區域Ⅲ的最薄板材厚度組合為8.49 mm、5.60 mm、5.27 mm。

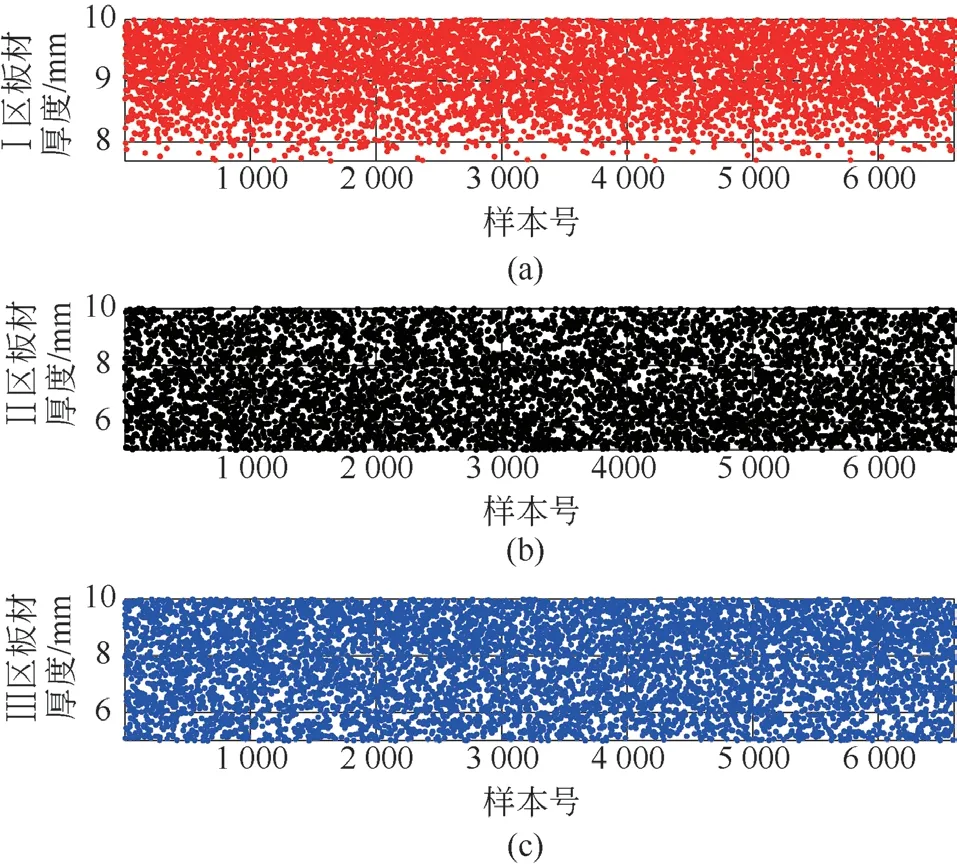
圖6 滿足條件的樣本點

4 優化結果二次驗證

考慮到板材厚度為標準化、系列化，取3個板材厚度分別為8.5 mm、5.6 mm、5.3 mm。相比優化前的10 mm初始厚度，主臂板材厚度下降了15%～47%，總質量降低了26%。將上述優化設計結果帶入原始有限元模型中，進行結果二次驗證確認。在機械臂主臂上，選取應力最大的區域內6個典型位置，計算每個位置危險有限元網格單元的米塞斯應力。圖7為一個工作循環中機械臂應力最大的6個區域的米塞斯應力曲線。

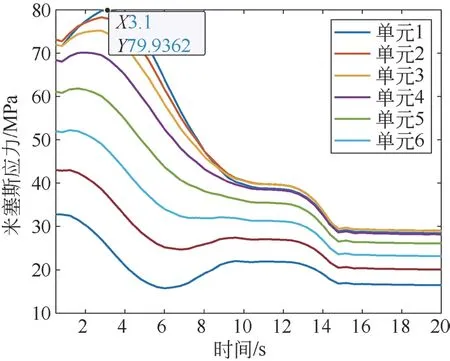
圖7 驗證優化設計結果

由圖7可知，優化設計后主臂在嚴苛工況下的一個工作循環0～20 s，6個危險位置的有限元網格單元米塞斯應力隨起吊、舉升、下降、卸載等過程發生連續變化，其中舉升過程米塞斯應力最大。工作過程中最大米塞斯應力為79.9 MPa，滿足4倍安全系數下許用應力的要求，且冗余量較小，同時也滿足輕量化設計目的。

5 結論

1）采用剛柔耦合動力學方法，建立了機械臂力學模型，計算了其在典型動態工作循環下的主臂受力情況，更精確地模擬了結構的真實受載狀態。

2）以機械臂輕量化設計為目標，以材料許用應力為約束條件，以主臂板材厚度為待優化參數，建立了待優化參數與約束條件之間的響應面模型，并進行了響應面質量檢驗。響應面可以在保證較高求解精度的同時，大大提高求解效率。

3）采用蒙特卡洛法對響應面模型進行優化求解，既可避免求解過程陷入局部最優，也可兼顧較高的求解效率。對優化結果進行二次驗證，證實本算法優化結果為全局最優，安全可靠。

4）從結構可靠性和輕量化角度對主臂優化結果進行評價。相比于原始方案，主臂板材厚度下降了15%～47%，總質量降低了26%，達到了輕量化、經濟性的目標，也為類似結構的優化設計，提供了良好的工程案例。