基于GMM的聽障兒童聽覺辨識能力機器檢測研究

徐 杰, 韓雪晴, 廖慶洲, 廖盛斌*

(1.華中師范大學經濟與工商管理學院, 武漢 430079;2.國家數字化學習工程技術研究中心, 武漢 430079; 3.武漢軟件工程職業學院人文學院, 武漢 430205)

1 聽障兒童聽覺辨識能力測試背景

聽覺是人類感知世界、接受信息的先天能力之一.聽障兒童由于聽覺能力先天性不足導致語言發展滯后,進行干預訓練成為發展聽障兒童聽覺能力的關鍵因素[1].目前,聽障兒童聽覺干預訓練廣泛采用聽覺口語法(auditory-verbal therapy,AVT),即通過聽力輔助設備,擴大并利用聽障兒童聽覺能力,進行個別化診斷式教學,主要訓練其傾聽能力,進而使之能開口溝通[2].聽覺口語法首要環節是測試聽障兒童聽覺辨識能力,檢查兒童能否辨識到正常言語頻率范圍內聲音.人工林氏七音是檢測兒童聽覺辨識能力一種簡便易行、行之有效的方法.

聽覺口語法是專業教師或治療師面向聽障兒童家庭提供的康復服務,教學時間通常為1～1.5 h,頻次一般為每周1～2次[4],通常聽覺干預訓練前聽障兒童需要分別測試雙側耳朵的情況.在專業教師緊缺的情況下,人工進行林氏七音測試耗時費力,縮減了聽障兒童學習聽力訓練時間,間接影響了聽障兒童聽覺能力發展進程.

語音識別技術的出現,為測試人員改良林氏七音測試帶來了新的可能性,語音識別技術因能夠將人類語言轉化成計算機可以讀取和識別的形式,實現人機交互,而被應用到工業、農業、軍事、交通、醫療以及教育等各行各業中[5].在教育領域中,劉文開等[6]研究利用語音識別建構智慧教室,提高智慧教室的信息化程度.曹雪燕等[7]研究了語音識別技術在聾人大學生課堂教學中的應用,認為使用語音識別技術彌補了手語對大學專業詞匯表達的不足.

針對人工檢測聽覺辨識能力存在耗時耗力的問題,將語音識別技術應用于聽障兒童聽覺辨識能力測試有望減少對人力的依賴,從而大幅提升效率.本文主要探討如何利用語音識別技術快速、高效測試聽障兒童聽覺辨識能力.

2 研究方法

本研究將采用語音識別算法針對聽障兒童林氏七音發音數據設計識別模型.目前,有許多算法應用于語音識別,如動態規劃算法[8]、高斯混合模型(Gaussian mixture model,GMM)[9]、隱馬爾科夫模型[10]以及RCNN[11]等,本研究在文獻研讀基礎上選取高斯混合算法對林氏七音建模,利用隱馬爾科夫模型進行對比實驗.

2.1 數據來源與處理

本研究使用的語音數據集來源于湖北省聾兒康復中心,錄制聽障兒童AVT課程13節.首先,對課程視頻進行分析,提取林氏七音音頻數據.接著,對數據進行清洗并人工標注,最終得到音頻數據91條.采用留出法將數據集D劃分為兩個互斥集合S訓練集70條和T測試集21條,部分音頻數據波形圖示例如圖1所示.

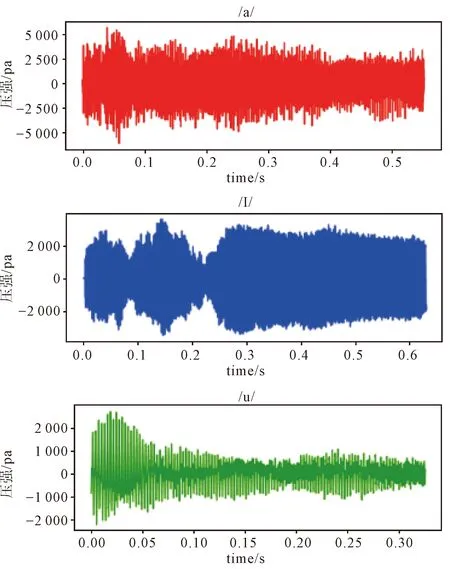
圖1 音頻數據集波形圖示例

2.2 聲學特征提取

聲學特征指表示語音聲學特性的物理量,是聲音諸要素聲學表現的統稱.如表示音色的能量集中區、共振峰頻率、共振峰強度和帶寬,以及表示語音韻律特性的時長、基頻、平均語聲功率等.

聲學特征提取是語音識別的關鍵步驟.提取聲學特征的方法有多種,如基于人耳聽覺特性梅爾頻譜系數(mel-frequency cepstral coefficients,MFCC)特征[12]、能量特征、頻譜特征[13]等,以及基于這些特征的融合與改進[14-15].其中,MFCC是一種廣泛應用于語音識別的特征參數[16-17].梅爾倒譜系數是在Mel標度頻率域提取出來的倒譜參數,Mel標度描述了人耳頻率的非線性特性,本研究利用Mel頻率倒譜系數提取林氏七音數據集的聲學特征,具體提取MFCC步驟如圖2所示.

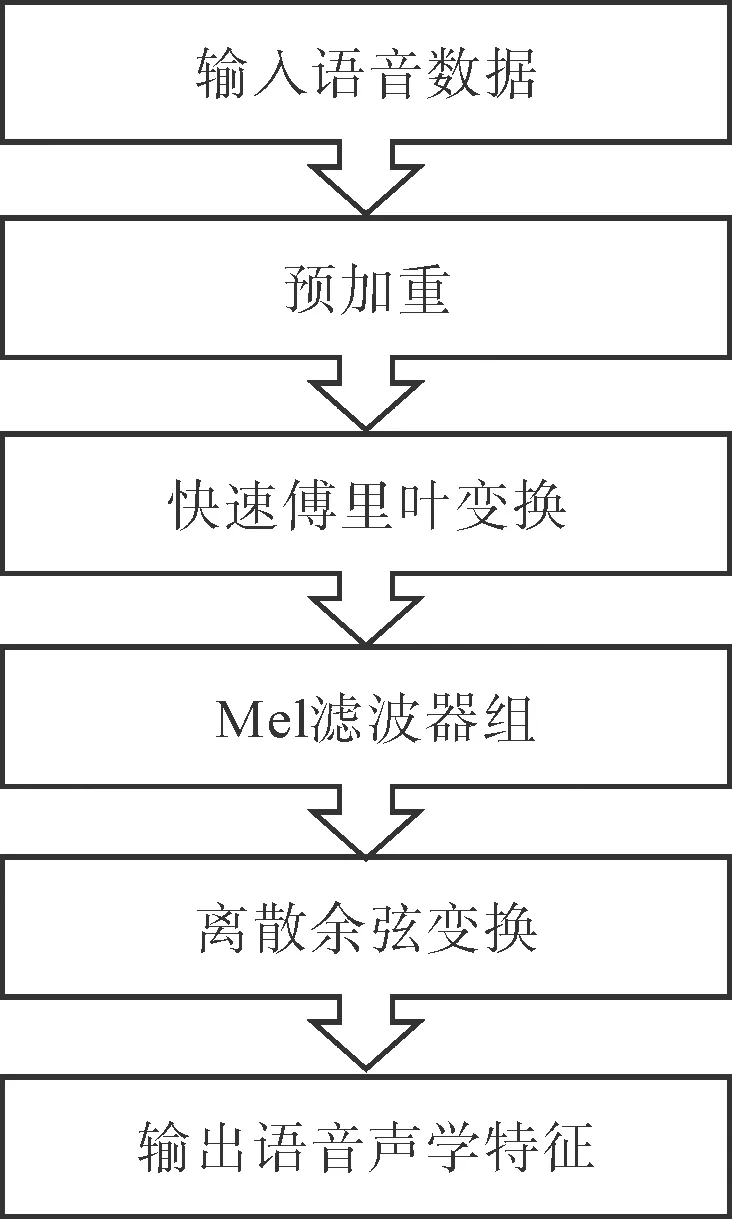
圖2 MFCC提取步驟

2.2.1 預加重 提取MFCC特征第一個階段是預加重,由于林氏七音中存在元音,可能出現頻率高而能量下降的聲譜斜移現象.采用預加重補償語音信號所壓抑的高頻部分,突顯高頻共振峰.

2.2.2 快速傅里葉變換 原始信號經過處理后,需要將時域信號轉化為頻域信號,抽取信號聲譜信息,利用快速傅里葉變換(Fast Fourier Transform,FFT)得到信號在頻譜上的能量分布.

2.2.3 Mel濾波器組 FFT計算得到的結果是關于每一個頻帶上能量大小的信息.由于人耳對不同頻率的敏感程度不同,且成非線性關系,因此需要將頻譜按人耳敏感程度分為多個Mel濾波器組,

用對數表示Mel聲譜值是由于人類對信號級別的反應按照對數計算,使用對數來估計特征時,對于輸入的變化也不太敏感.

2.2.4 離散余弦變換 由于濾波器之間是有重疊的,Mel濾波器組計算出的濾波器組系數高度相關,應用離散余弦變換去除相關濾波器組系數并產生濾波器組的壓縮表示,獲得最后的特征參數.

將林氏七音音頻數據集部分MFCC進行可視化,如圖3所示.

圖3 數據集MFCC示例

2.3 建立聲學模型

在建立模型階段,通過高斯混合模型為提取的聲學特征矢量建模并指派聲學似然度.

單變量高斯分布通過參數一個均值μ和一個方差σ2來定義,可以對一個單獨的倒譜特征計算聲學似然度[18].由于MFCC是一個多維的矢量,可以使用多變量高斯分布來指派聲學似然度.多變量高斯分布使用N維的均值矢量μ和協方差矩陣Σ來定義.

多變量高斯分布將特征矢量每一個維度作為高斯分布來建模,而一個特定的倒譜特征可能非正態分布,高斯混合模型通過把若干個多變量高斯分布加權混合建模以避免非正態分布的情況,高斯混合模型如下式所示,

f(x│μ,Σ)=

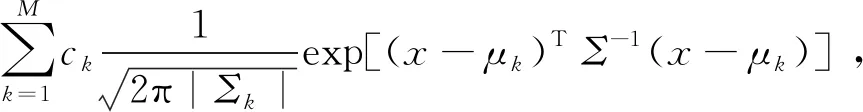
其中,μ為均值,Σ為協方差矩陣,ck為混合系數,M為混合的高斯分布個數.

2.4 訓練聲學模型

訓練聲學模型通過計算高斯混合模型參數最大化聲學似然值.本文將采用測試集訓練聲學模型,利用EM算法估計模型中參數,具體步驟如下.

1) 音頻聲學特征作為樣本集D={x1,x2,…,xn}.

2) 初始化高斯混合模型的參數μ、Σ、ck.

3) E步:根據當前參數計算每個樣本屬于每個高斯成分zi的后驗概率

γij=P(zj=i|xj).

4) M步:計算新的均值μ,

計算新的協方差矩陣Σ,

計算新的混合系數ck,

重復以上E步、M步,將最終得到的參數代入到目標函數中完成模型.

3 實驗結果與性能評估

將林氏七音測試識別設計為一種多分類任務,七音分別代表七個種類.多分類任務的評估指標比較復雜,一般將多分類任務視為n個二分類任務.對n個二分類任務通常使用宏平均(macro-average)、微平均(micro-average)、加權平均(weighted-average)等方法評估模型表現情況.其中,宏平均計算方法區分樣本不同類別,先分別計算每個類別的Precision、Recall,然后所有類別度量值平均.微平均不區分樣本類別,計算整體的Precision、Recall.加權平均是對宏平均的一種改進,考慮了每個類別樣本數量在總樣本中占比,為樣本分配權重.由于本研究利用留出法劃分數據集,為每種樣本分配相同數量音頻,在此基礎上綜合考慮三種評估指標,最終采用宏平均中Macroprecision(式(1))和Macrorecall(式(2))作為評估模型的指標.宏平均注重區分類別,缺乏對整體數據集的考察,選取精確率(式(3))作為補充,評估模型在整體數據集的表現情況.

(1)

其中,PrecisionPj的計算方法如下:

(2)

其中,RecallRj的計算方法如下:

(3)

在二分類任務中,TP、FP、TN、FN分別為被模型預測為正類的正樣本、被模型預測為正類的負樣本、被模型預測為負類的負樣本、被模型預測為負類的正樣本,具體如表1所示.

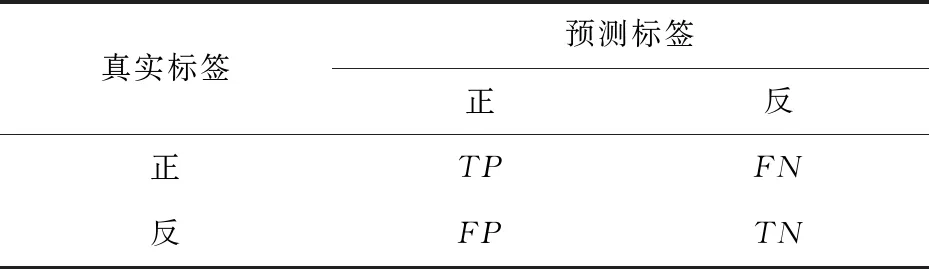
表1 評估模型

多分類任務可以用一個混淆矩陣來表示,混淆矩陣是一個n×n的矩陣,n表示多分類的類別數,混淆矩陣對角線上表示的是分類正確的樣本.行代表了真實類別,列代表了預測類別.圖4為高斯混合模型的混淆矩陣.

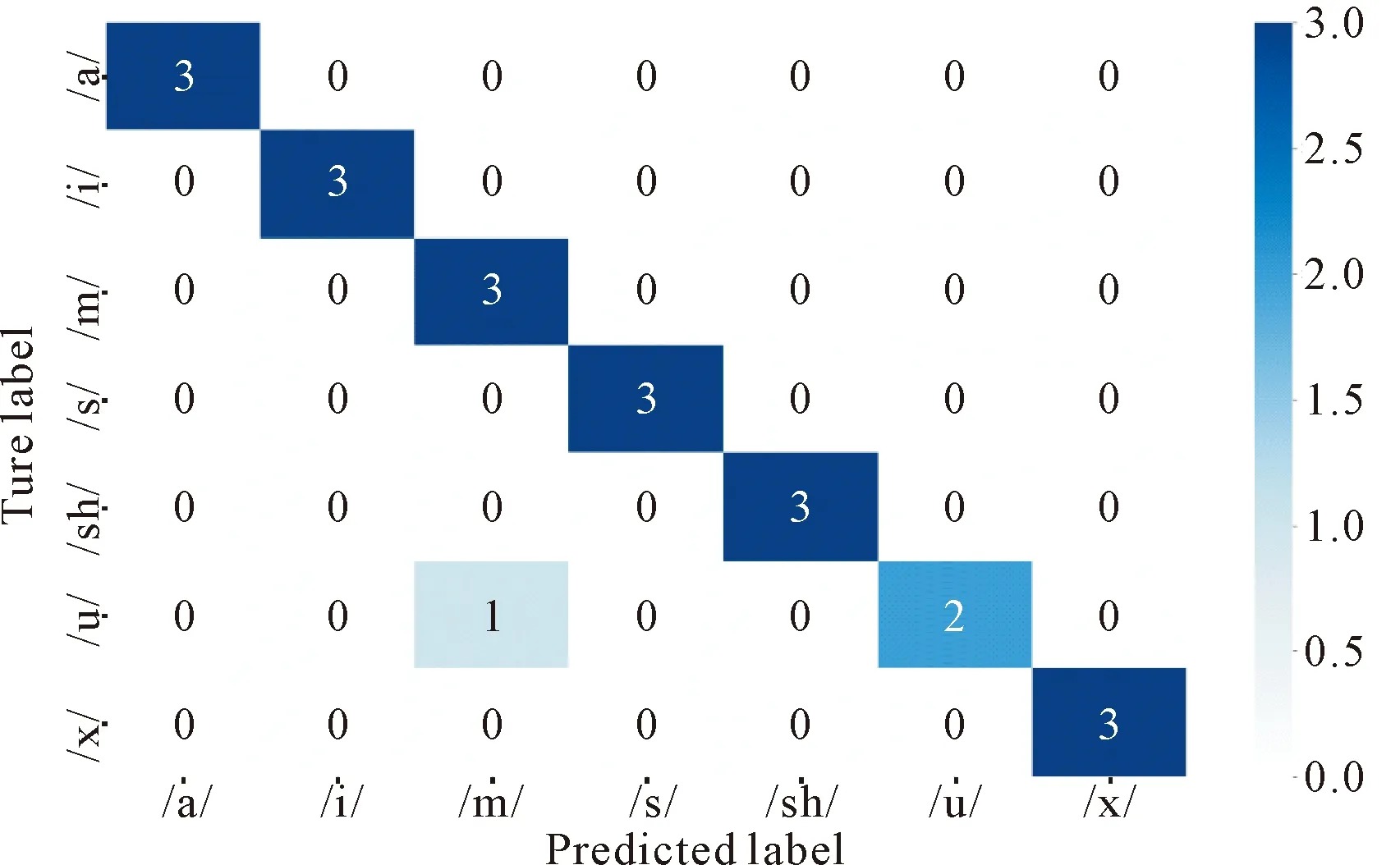
圖4 GMM混淆矩陣

Macro precision、Macro recall兩種指標只反映了模型對數據集整體的表現,表2展示了高斯混合模型每個音的具體分類以及準確率表現情況.

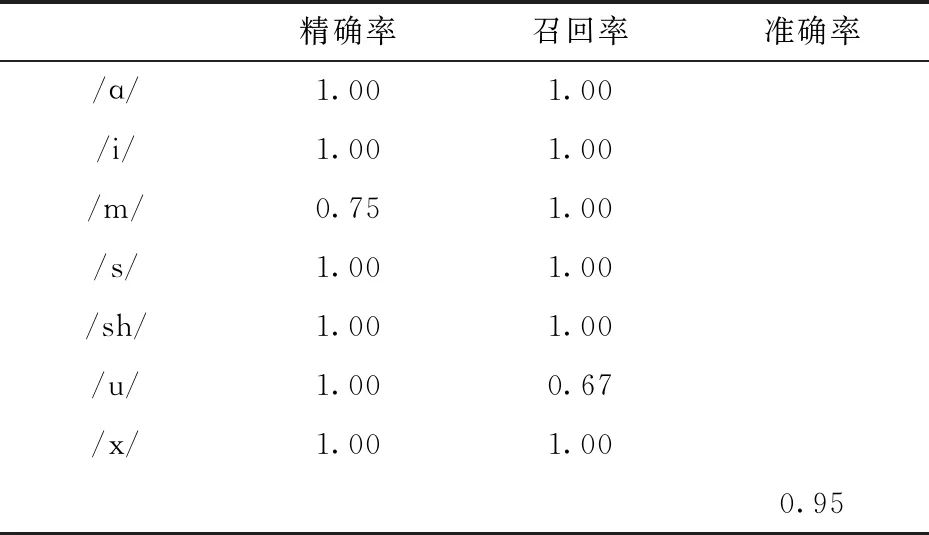
表2 GMM分類報告

實驗結果表明,高斯混合模型林氏七音分類精確率為0.96, 召回率為0.95,準確率為0.95,其中,/m/音預測正確的數量低于其他六音,/u/音真實正例被分類器召回數量低于其他六音.

3.1 高斯混合模型與隱馬爾科夫模型對比

為了進一步驗證高斯混合模型在機器識別林氏七音中的準確性,本研究分別采用高斯混合模型和常用來處理音頻數據的隱馬爾可夫模型對相同數據集建模進行對比實驗,圖5為隱馬爾科夫模型預測類別的預測結果與真實結果.

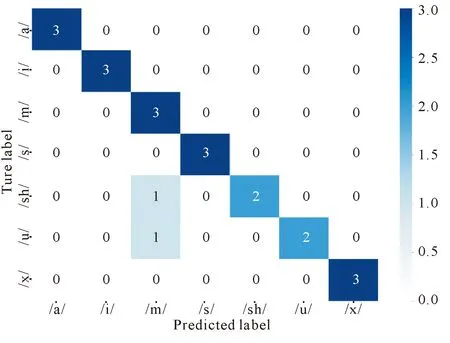
圖5 HMM模型預測類別結果

HMM每個音具體分類以及Accuracy表現情況如表3所示.

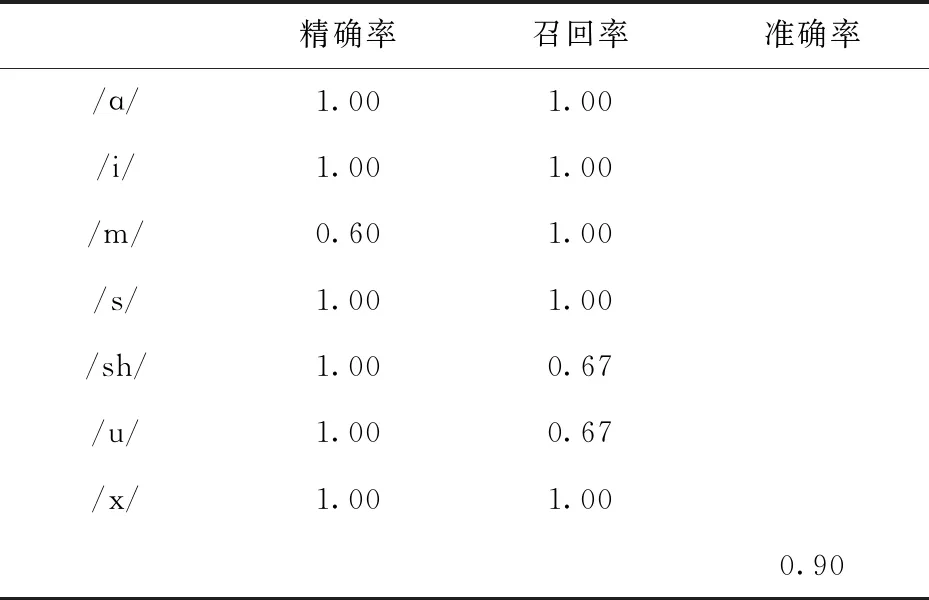
表3 HMM分類報告

最終,HMM模型分類的精確率為0.94, 召回率為0.90,準確率為0.90.兩種模型實驗在三個指標中對比情況如表4所示

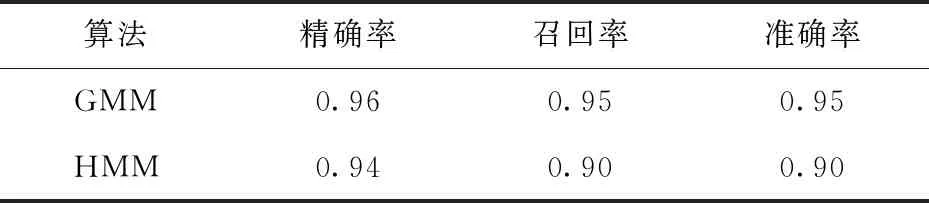
表4 GMM與HMM的表現比較

實驗結果表明,高斯混合模型在正確分類的數量以及分類的精確率上有較大優勢,在總體三個指標的性能表現中也均優于HMM模型,能夠較好地識別林氏七音.

4 結論

本研究提出了一種基于高斯混合模型的機器識別普通話版林氏七音測試方法.首先,在湖北省聽障兒童康復中心采集并制作林氏七音數據集;接著,提取普通話版林氏七音數據集的聲學特征;然后在普通話版林氏七音訓練集的基礎上建立并訓練高斯混合聲學模型,將模型設計為多分類任務,通過Macro precision、Macro recall、Accuracy三個指標評估模型的表現情況.本研究將高斯混合模型和隱馬爾可夫模型在同一數據集上進行對比實驗,結果表明,基于高斯混合模型林氏七音測試模型能更好的識別普通話版林氏七音.