橫向噴流對低速大攻角細長旋成體非對稱氣動特性影響研究

徐一航 劉 偉 ,?,

* (江南機電設計研究所,貴陽 550000)

? (南京航空航天大學航空學院,南京 210016)

引言

垂直發射導彈在頭部安裝側向噴流裝置是實現導彈快速轉彎的技術之一[1].導彈在垂直發射離筒后的短時間內,須完成導彈的快速大角度轉彎,尤其是當橫風非常大的時候(如較大的臺風、甲板風等),導彈初始時刻的速度較低、而橫風速度很大,這就導致了導彈在剛發射的短時間內處于低速大攻角狀態.因此,需要對低速大攻角條件下細長旋成體橫向噴流的氣動特性有足夠的認知.

目前,國內外已有許多學者對低速條件下無噴流細長旋成體的大攻角氣動特性進行了研究.Allen等[2]首次在實驗中發現大攻角時細長旋成體背風面會產生非對稱渦,使得細長旋成體在大攻角時會產生側向力.Siclari 等[3]的研究證實了非對稱流動是真實存在的,而不是由數值模擬誤差引起的.細長旋成體大攻角非對稱流場產生的原因分為兩種:流體動力不穩定性[4]和流動分離的不對稱性[5].Jiménez等[6]對細長旋成體從流體動力穩定性方面進行了分析,采用數值模擬和試驗相結合的方法對比分析了細長旋成體的渦量分布,認為全流場都存在不穩定性;在流動分離的不對稱研究方面,Obeid 等[7]認為分離點微小的不對稱會導致兩側剪切流不一致,而兩側剪切流不一致是造成分離渦不對稱的原因.Taligoski 等[8-10]進一步解釋了邊界層會影響剪切流的不對稱性,導致背風區分離渦非對稱現象的產生,并研究了頭部存在微小加工缺陷時旋成體的側向氣動特性和表面壓力分布特性.Moskovitz 等[11-12]研究了頭部粗糙度對細長旋成體大攻角非對稱流場的影響.大量試驗[13-15]和數值模擬[16-19]的結果都表明:細長旋成體頭部的初始非對稱擾動會觸發下游流場強烈的非對稱性.

在大攻角橫向噴流方面:梁偉等[20-21]對亞、跨、超聲速大攻角條件下細長旋成體的氣動特性進行了研究,分析了自由來流與噴流之間的相互干擾對旋成體法向氣動特性的影響.Wang 等[22]分析了尾部帶有橫向噴流的細長旋成體大攻角條件下的法向氣動特性.Zhang 等[23]對橫向噴流條件下大攻角細長旋成體不對稱分離特性進行了研究,分析了馬赫數為0.3～0.8 條件下細長旋成體的側向氣動特性.葉楠等[24]對微吹氣前體細長旋成體進行了試驗研究,分析了不同攻角下吹氣量對細長旋成體非對稱流動分離的控制效應及其流動機理.

從細長旋成體的研究情況來看,對于無噴流低速大攻角條件下的非對稱氣動特性國內外學者已經進行了較為詳細的研究.對于有噴流大攻角條件下的非對稱氣動特性研究較少且主要集中在亞音速,只有少部分學者從流動控制角度對微吹氣前體細長旋成體的非對稱流動分離進行了研究.本文對直接力控制下(大吹氣量)細長旋成體橫向噴流在低速大攻角條件下的非對稱氣動特性進行研究,通過測力風洞試驗捕捉大攻角非對稱現象,采用數值模擬方法對大攻角非對稱現象的流場特性進行分析,為低速大攻角細長旋成體的橫向噴流設計提供理論基礎.

1 測力風洞試驗

1.1 風洞裝置

實驗在南京理工大學HG-1 風洞中進行,該風洞為開口環流式風洞.風洞實驗段截面積為700 mm×700 mm、長1.1 m、速度范圍為0.1～25 m/s,湍流度0.97%.

1.2 天平載荷能力與靜校指標性能

風洞的天平載荷能力與靜校指標性能如表1 所示,天平的靜校中心距離前端面距離為83.00 mm.

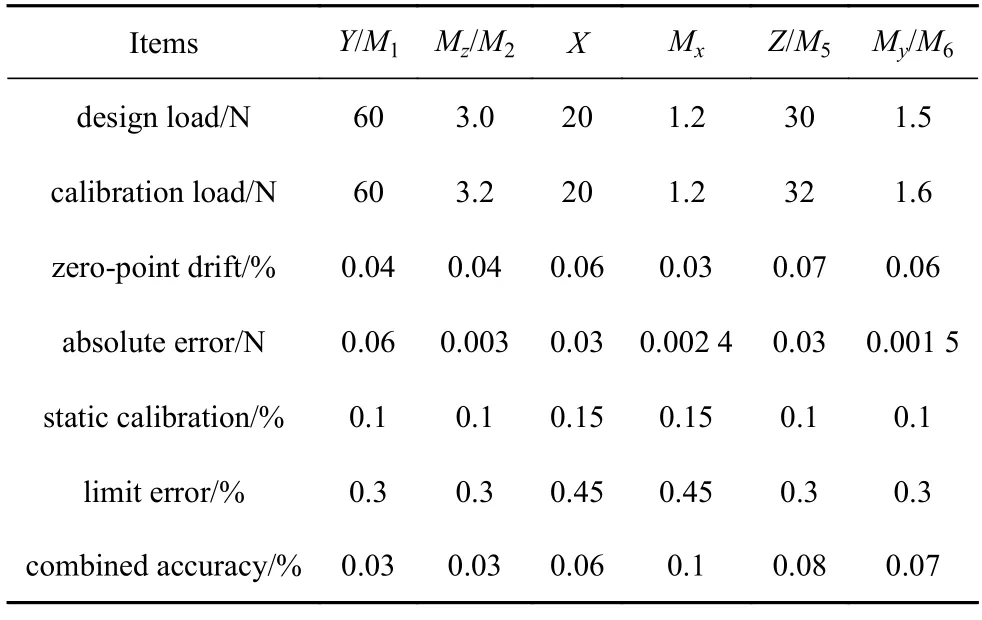
表1 天平載荷能力與靜校指標性能Table 1 Balance load capacity and static calibration index performance

1.3 噴流模型試驗裝置

如圖1 所示為噴流模型試驗裝置示意圖,坐標系定義如下:xoy平面為風洞試驗裝置的俯視圖平面.ox為來流方向,oy垂直于ox指向風洞外側,oz的方向由右手定則確定指向上方.xoy為攻角平面,定義旋成體的攻角α沿oz軸逆時針旋轉為正,攻角范圍為-80o～80o.活塞式壓氣機將高壓氣體壓縮到氣瓶內,通過調節減壓閥得到穩定的氣流輸出.

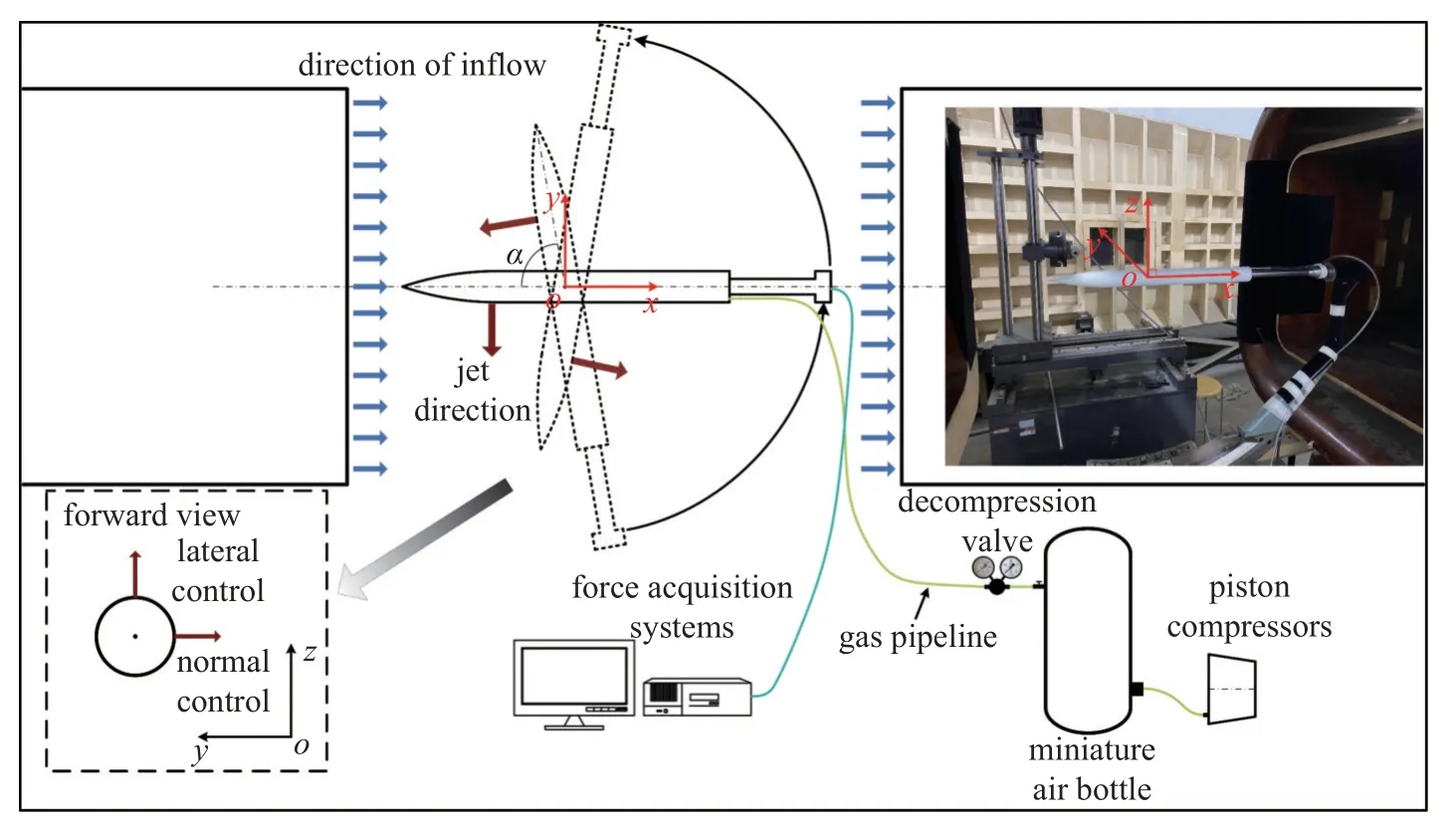
圖1 噴流模型試驗裝置示意圖(俯視圖)Fig.1 Schematic diagram of the jet model test setup (top view)

如圖2 所示為模型尺寸圖,細長旋成體的長細比為12.5,長度為500 mm.橫向噴流采用漸縮噴管,噴管入口處截面半徑為2.25 mm,出口處截面半徑為1 mm,噴管與后方輸氣管相連,噴口中心距離頭部122.0 mm,在旋成體頭部xoy平面、oz正向位置安置一個固定的擾流片.

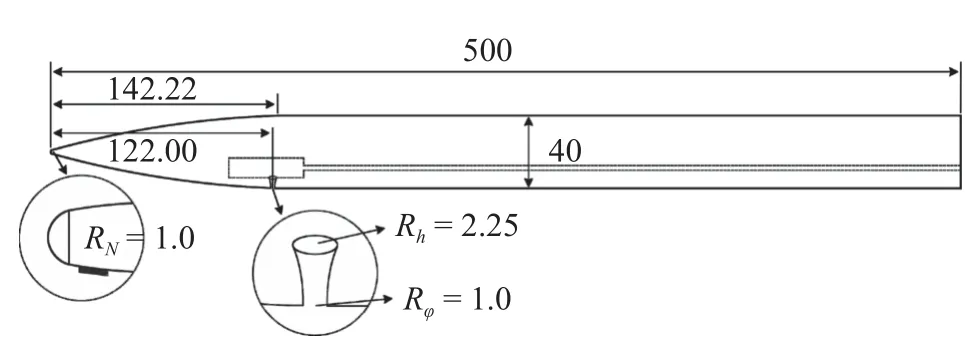
圖2 模型尺寸圖(單位:mm)Fig.2 Dimensional diagram of the model (unit:mm)

1.4 試驗工況說明

試驗雷諾數為Re=55000 (參考長度為直徑D=40 mm),橫向噴流的總壓為0.406 MPa,將熱線探針置于噴管出口處測得出口速度為237.1 m/s.相關試驗參數如表2 所示,攻角范圍-80o～80o,每5o采集一次測力數據,每組數據采集時間為10 s,采樣頻率5 kHz.

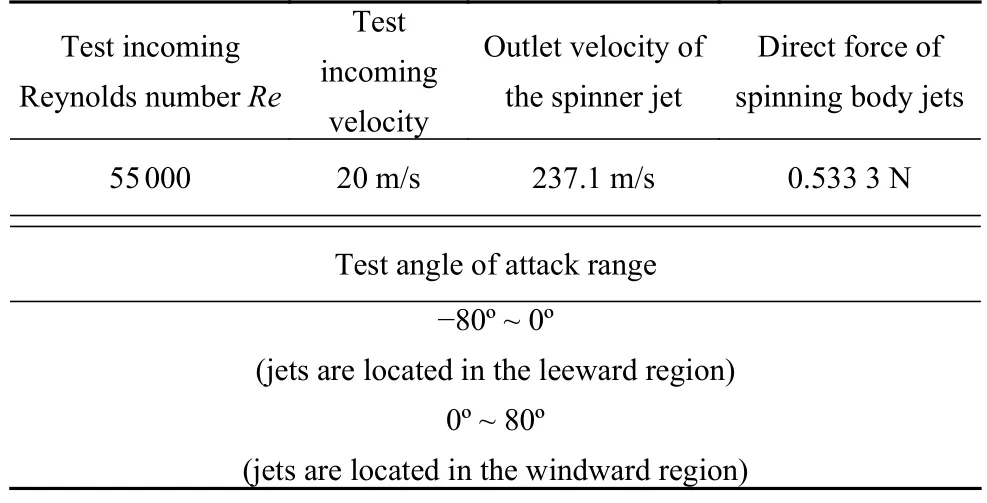
表2 試驗參數表Table 2 Test parameters

進行兩組橫向噴流試驗,自由來流方向為ox,噴流方向分別為oy負向和oz正向(如圖1 中前視圖所示),xoy為攻角平面.oy負方向打開橫向噴流為旋成體進行法向控制,oz正方向打開橫向噴流為旋成體進行側向控制.

1.5 試驗分析示意圖說明

為了能夠更加清晰地分析細長旋成體在噴流影響下的非對稱特性,對試驗分析做如下定義:試驗工況中細長旋成體攻角的正、負性切換代表了法向控制時噴流出口由迎風面切換到背風面,因此在試驗結果分析時采用如圖3 所示的方式將法向控制時的噴流分為迎風區噴流和背風區噴流來分析.側向控制時由于正、負攻角情況下流動是對稱的,因此分析其正攻角情況下的非對稱特性.如圖3 所示在分析試驗結果時定義軸向方向為ox,法向方向為oy,側向方向為oz,定義Cz為側向力系數.

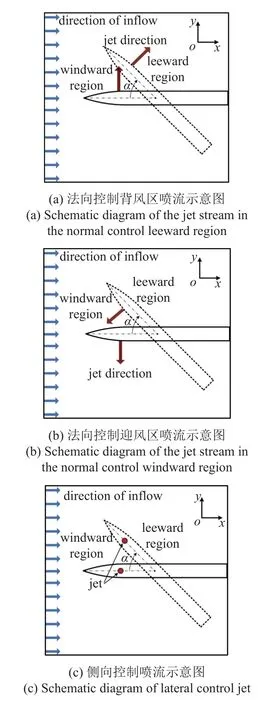
圖3 噴流試驗結果分析示意圖Fig.3 Diagram of the analysis of the jet test results

1.6 試驗結果

1.6.1 細長旋成體法向控制側向力系數

如圖4 所示為法向控制時細長旋成體側向力系數隨攻角變化曲線,圖中給出了無噴流和噴流處于迎、背風區時旋成體側向力系數隨攻角變化曲線.

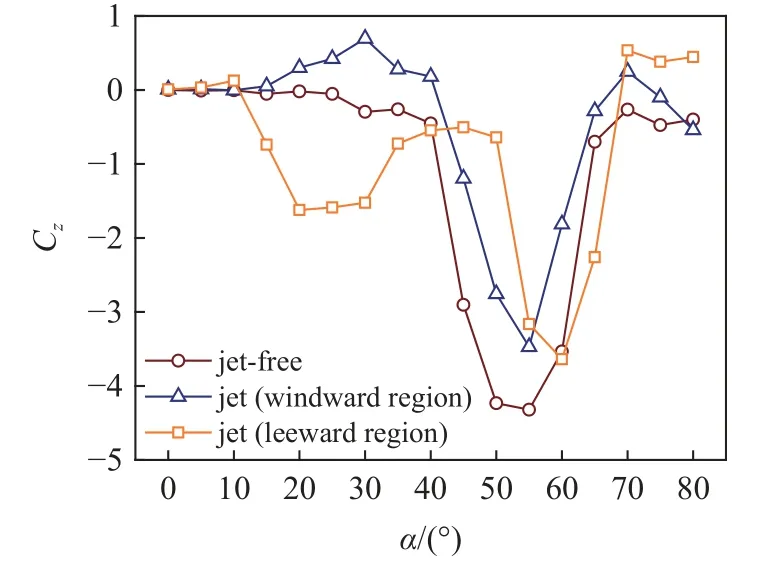
圖4 法向控制時細長旋成體側向力系數隨攻角變化曲線Fig.4 Variation of lateral force coefficients with angle of attack for normal control of slender spiniform bodies

當沒有橫向噴流時:側向力系數在攻角0o～25o范圍內幾乎為0,當攻角大于25o之后側向力系數絕對值開始逐漸增加,并在55o時達到峰值.當橫向噴流處于迎風區時:攻角大于15o后側向力系數絕對值逐漸增加,但是攻角范圍在20o～40o之間有噴流和無噴流時旋成體所產生的側向力方向相反.攻角大于40o之后側向力系數的方向發生了改變,與無噴流時的側向力系數方向相同,但是其絕對值要比無噴流時的側向力系數小.當橫向噴流處于背風區時:攻角小于10o情況下側向力系數絕對值較小,但是攻角在15o～35o之間有噴流時的側向力系數絕對值要明顯比無噴流時大,在隨后的35o～50o之間旋成體側向力系數絕對值變小,之后又變大并在60o時達到峰值,但是其產生較大側向力的攻角要比無噴流時大.

如圖5 所示為無噴流時細長旋成體側向力系數曲線和功率譜密度(PSD),當攻角較小時沒有發現明顯的主頻,此時旋成體的側向力系數為0.隨著攻角的增加旋成體的側向力系數增大,其功率譜密度出現了較為明顯的主頻.小攻角時旋成體的側向力系數平均值較小、振蕩幅值較低,隨著攻角的增大側向力系數平均值增大,彈身渦呈現周期性脫落.當攻角為55o時,旋成體的側向力系數平均值也較大且其幅值震動較大,由非對稱渦分離所導致的旋成體側向力系數周期變化曲線變得較為無序.

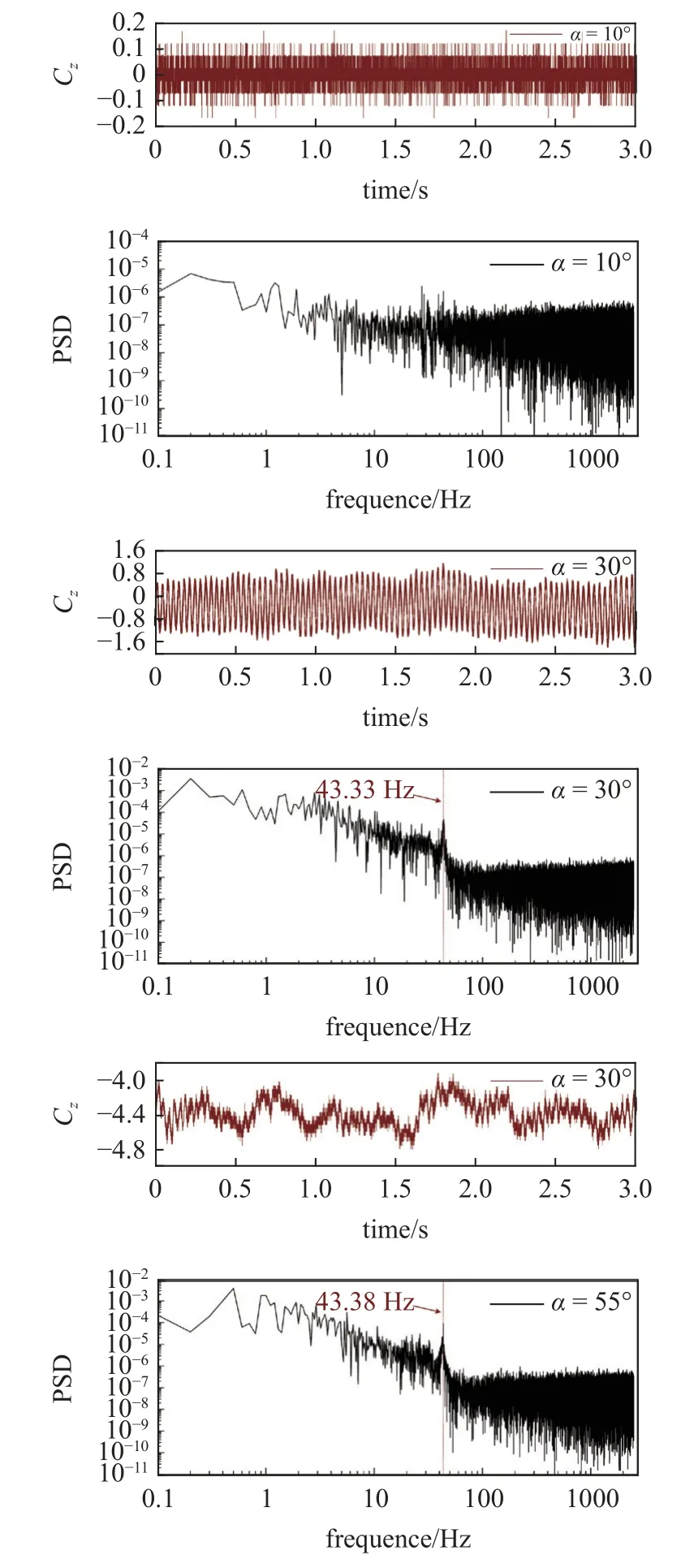
圖5 無噴流時細長旋成體側向力系數曲線和功率譜密度(法向控制)Fig.5 Lateral force coefficient curves and power spectral densities(PSD) of slender spiniform without jets (normal control)

從以上分析可以看到,不同攻角下細長旋成體的非定常流動體現出了不同的側向力特性,主要分為以下兩種情況:首先是攻角較小時,旋成體表面無流動分離和非對稱渦脫落,此時側向力系數平均值很小、其功率譜密度無明顯主頻.其次是攻角較大時,由于渦的非對稱分離和脫落所誘導的較低主頻.因此將特征頻率進行無量綱化,提取出脈動主頻的斯特勞哈爾數St

式中,f為側向力系數的脈動主頻,D為細長旋成體直徑,V為來流速度.

圖6 為有、無噴流時細長旋成體的斯特勞哈爾數,有、無噴流情況下斯特勞哈爾數的變化規律都是隨著攻角的增大先減小后增大、再減小.噴流處于背風區時細長旋成體的斯特勞哈爾數普遍要比無噴流時大,噴流處于迎風區時細長旋成體的斯特勞哈爾數普遍要比無噴流時小,這說明噴流在迎風區和背風區對細長旋成體非對稱流動分離所產生的脫落渦影響不同,使得脫落渦的主頻發生了改變.

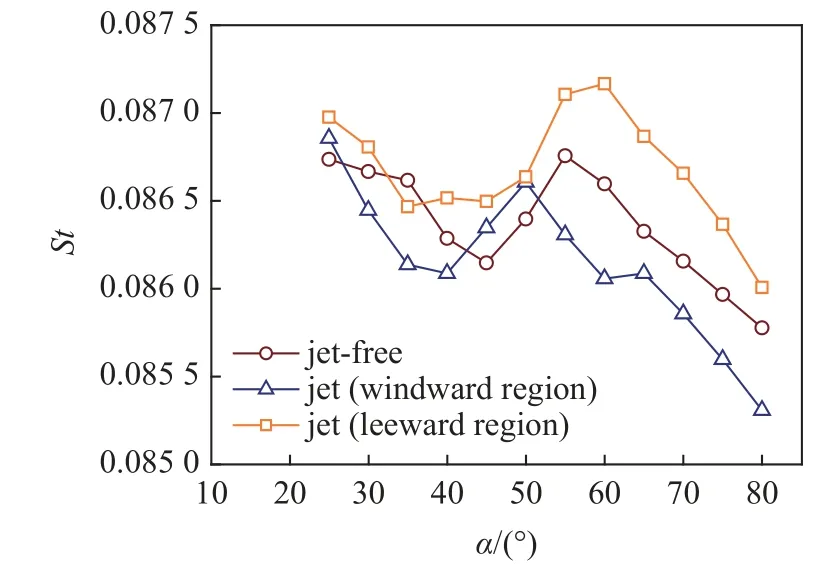
圖6 有、無橫向噴流時細長旋成體斯特勞哈爾數(法向控制)Fig.6 Strouhal number of slender spiniform with and without transverse jets (normal control)

1.6.2 細長旋成體側向控制側向力系數

如圖7 所示為有、無橫向噴流時細長旋成體側向力系數隨攻角變化曲線,此時噴流方向為oz(即噴流對旋成體進行側向控制).有、無噴流時旋成體的側向力系數在正負攻角時的變化規律是相同的,因此此處只展示正攻角的情況.當有噴流時小攻角條件下旋成體也存在較大的側向力系數,這是由于噴流產生的直接作用力所導致的.但是當攻角增加到25o時側向力系數絕對值開始減小,在攻角為35o時旋成體的側向力系數幾乎為0,這說明此時由于旋成體不對稱流動分離所導致的側向力與橫向噴流所產生的直接作用力方向相反、大小相當.隨著攻角的進一步增大側向力系數絕對值逐漸增大,并在50o時達到最大值隨后減小,其側向力系數絕對值的最大值要比無噴流時大.

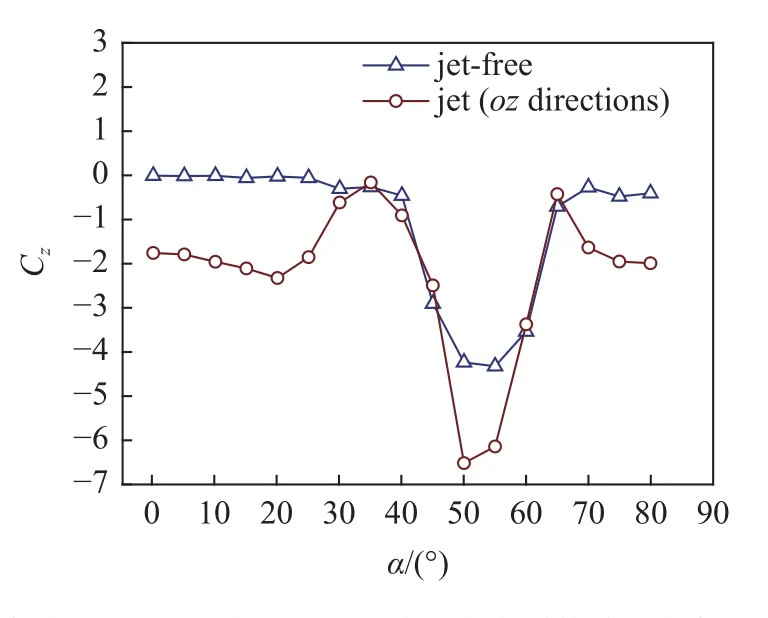
圖7 橫向噴流oz 方向細長旋成體側向力系數隨攻角變化曲線(側向控制)Fig.7 Lateral force coefficient curve of slender spiniform with angle of attack in the direction of transverse jet oz (lateral control)

圖8 為有、無噴流時細長旋成體進行側向控制時的斯特勞哈爾數,有噴流時的斯特勞哈爾數明顯比無噴流時大.旋成體進行法向控制時斯特勞哈爾數隨攻角的變化規律與無噴流時的趨勢是相同的,但旋成體進行側向控制時斯特勞哈爾數隨攻角的變化規律與無噴流時有較大的差別,這說明沿oz方向進行噴流時噴流對旋成體脫落渦的主頻產生了較大的影響.

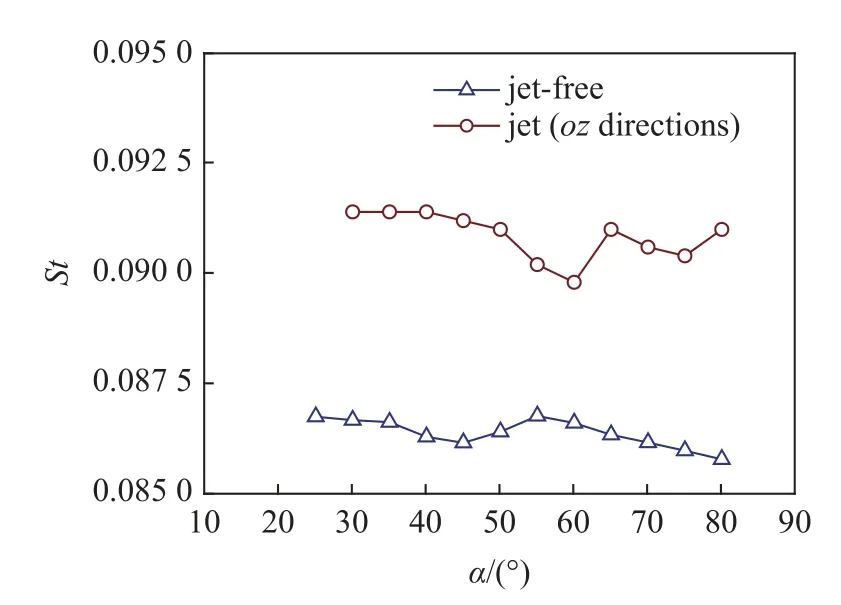
圖8 有、無橫向噴流時細長旋成體斯特勞哈爾數(側向控制)Fig.8 Strouhal number of slender spinner with and without transverse jets (lateral control)

2 數值計算分析

為了進一步分析橫向噴流對細長旋成體大攻角非對稱氣動特性的影響,采用數值模擬方法對有、無橫向噴流條件下的細長旋成體氣動特性進行分析.

2.1 數值方法與可信度驗證

采用基于k-ωSST 的DES 方法[25-26],DES 方法是一種用于解決三維非定常大分離流動的湍流求解方法,DES 方法在近壁面網格分辨率不適合大渦模擬(LES)的區域使用雷諾平均(RANS)湍流模型,遠壁面網格分辨率不適合RANS 的區域使用LES,具有較高的精度.

SST-DES 方法是在兩方程SST 模型基礎上提出的DES 類混合方法,其模型方程如下

其中,FDES為SST-DES 方法的開關函數

式中,LRANS為RANS 模型的特征尺度,FDES在近壁面等于1,在遠壁面大于1.網格尺度Δ為3 個空間方向上的最大網格步長,CDES為自適應參數

算例驗證采用DES 方法對細長旋成體進行數值模擬,與文獻中的風洞實驗結果進行了對比[9].文獻中的細長旋成體直徑62 mm,前段為尖拱型的錐柱體長細比為2,模型全長L=700 mm,長細比L/D=11.3,文獻中試驗來流雷諾數Re=55000,實驗結果得到的是細長旋成體側向力系數隨攻角變化曲線.數值模擬驗證計算網格量為1430 萬,設置非定常流動的時間步長為Δt=1.0×10-5s,旋成體前方采用速度入口邊界條件,后方采用壓力出口邊界條件,結果如圖9 所示,細長旋成體側向力系數隨攻角變化規律與實驗值吻合較好,因此采用DES 方法對旋成體的流動分離進行計算具有可信性.

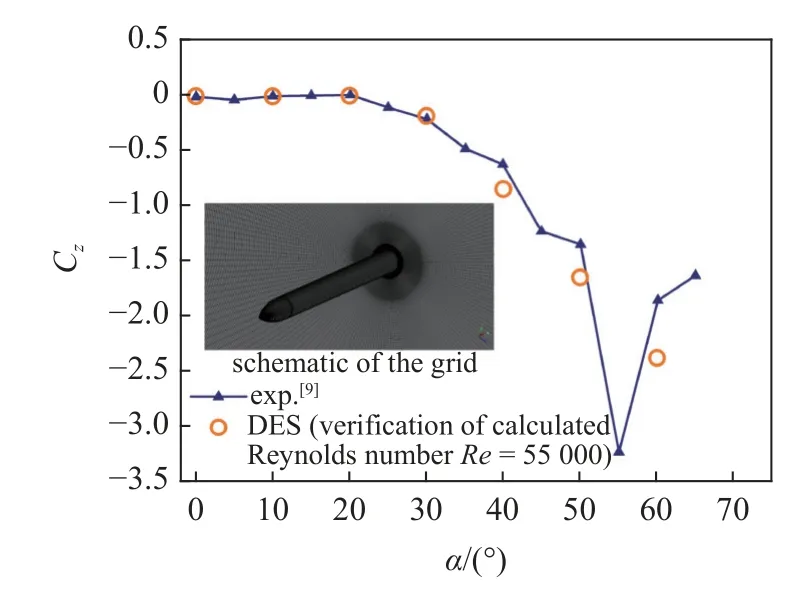
圖9 細長旋成體側向力系數對比圖Fig.9 Comparison of lateral force coefficients for spinning bodies

2.2 細長旋成體網格及其數值驗證

如圖10 所示采用O 型網格拓撲,遠場網格向前延伸8 倍彈長,向后延伸8 倍彈長,徑向約20 倍彈徑.貼近物面的第一層網格厚度保持y+～1 以確保邊界層的準確模擬,將網格內邊界設置為無滑移絕熱壁,細長旋成體前方采用速度入口邊界條件,后方采用壓力出口邊界條件,噴嘴處采用速度入口邊界條件,對細長旋成體有、無橫向噴流時的流場進行數值模擬,對細長旋成體進行數值模擬時的雷諾數Re=55000.

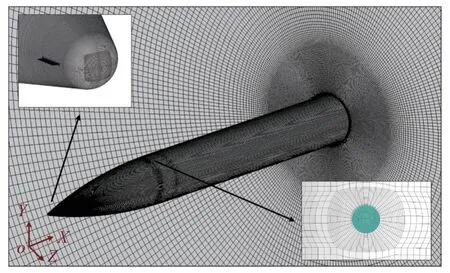
圖10 細長旋成體網格示意圖Fig.10 Grid schematic of slender spinner

表3 為采用4 套網格進行網格無關性驗證時網格的相關參數表,網格量分別為540 萬、1020 萬、1570萬和2080 萬,4 套網格采用相同的第一層網格高度和不同的近壁面網格增長率.利用普朗特假定的順流光滑平板紊流邊界層厚度計算公式δ=0.37(Rex)-1/5x預測邊界層厚度,計算時間步長均為1.0×10-5s.從表中的計算結果可以看出網格量的增加對側向力系數的計算結果有一定的影響,隨著網格量的增加,當網格量達到1570 萬以上時其側向力系數變化較小,因此最終選擇1570 萬網格進行數值計算.圖11 為時間步長無關性驗證的結果,分別選擇5.0×10-5,2.0×10-5,1.0×10-5和5.0×10-6s 這4 個時間步長進行計算,隨著時間步長的減小側向力系數變化逐漸變小,最終選擇時間步長為1.0×10-5s,每一次步長的內迭代為60 次.數值計算中坐標系的定義與試驗分析時相同(即圖3 所示),法向控制時噴流分為迎風區和背風區,側向控制時噴流沿oz正向.

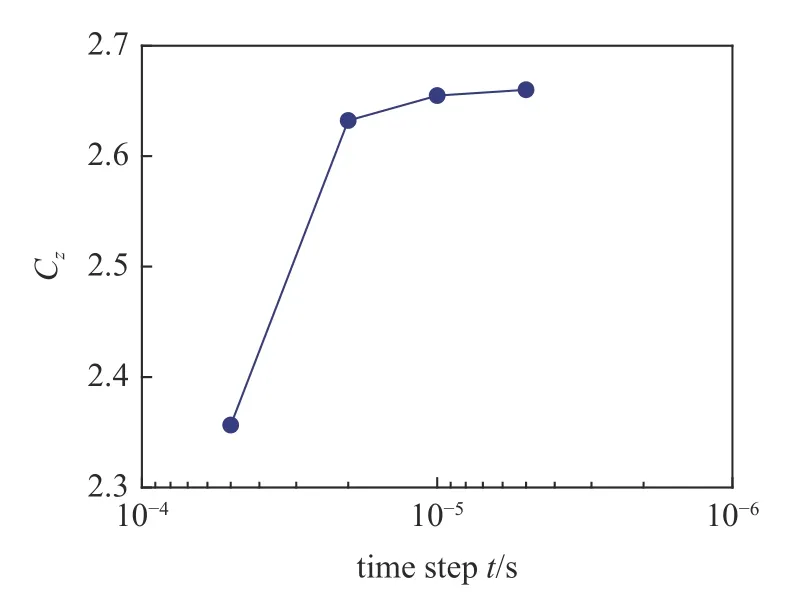
圖11 數值模擬結果與試驗值對比圖Fig.11 Comparison of numerical simulation and experimental values

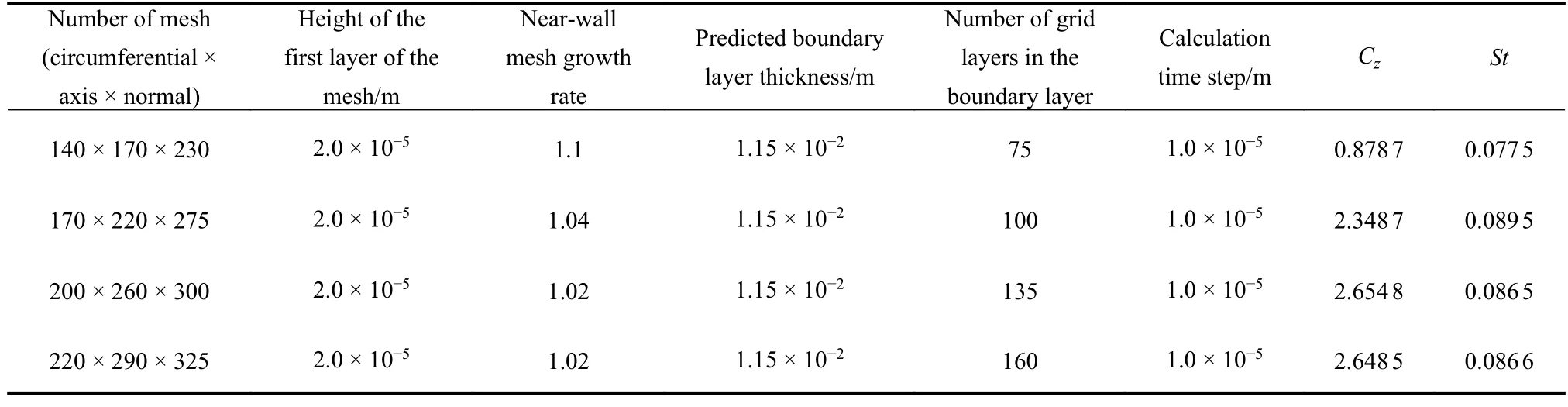
表3 網格無關性驗證參數表Table 3 Verification of grid-independence

圖12 為采用基于k-ωSST 的DES 方法計算得到的周期平均側向力系數與試驗值的對比圖,結果表明采用DES 方法能夠較為準確地模擬細長旋成體低速大攻角下的非對稱氣動特性.

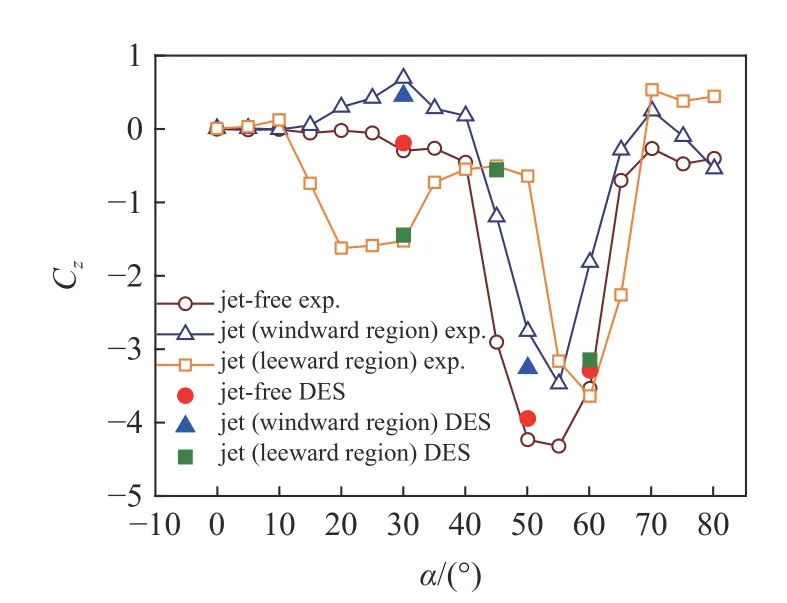
圖12 時間步長無關性驗證Fig.12 Time step independence verification

2.3 細長旋成體法向控制數值模擬

2.3.1 噴流位于細長旋成體背風區

當細長旋成體噴流位于背風區時其側向力特性與無噴流相比會發生改變,最為明顯的是當攻角處于15o～35o之間時有噴流旋成體的側向力系數絕對值要明顯比無噴流時大.圖13 為α=30o時有、無噴流條件下(噴流位于背風區)旋成體流線圖,當無噴流時旋成體背風區的流動分離較為對稱,從頭部拖出的流線可以看出其流動分離點的位置較為接近,有擾流片的一側先發生流動分離,在彈體的后段先產生高壓區.但是當噴流存在時,旋成體背風區的流動分離出現了明顯的非對稱特性.在噴流的影響下旋成體無擾流片一側的流動首先發生了分離,而有擾流片一側的流線在左側流動分離的影響下向彈體左側流動,從而使得彈體右側出現大面積高壓區,產生較大的側向力.

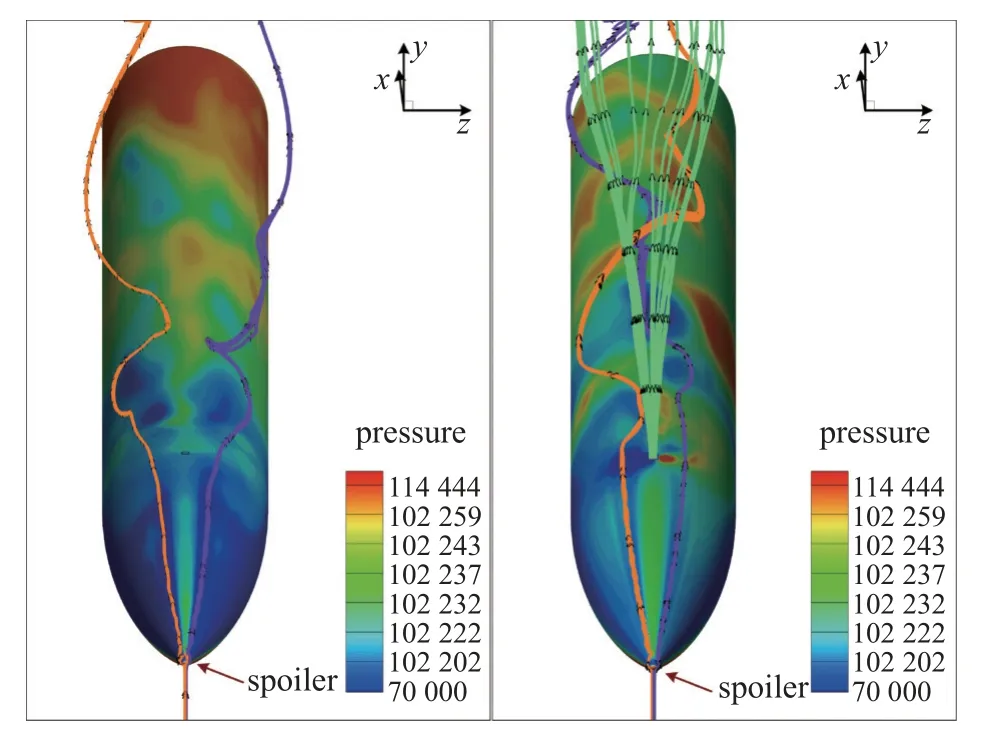
圖13 α=30o時有、無噴流旋成體流線圖(噴流位于背風區)Fig.13 Comparison of vortex volume of spinner with and without jets at α=30o

從圖14 中的三維流線圖可以看出從頭部拖出的左右兩側流線在受到噴流影響之后距離彈體的高度不同,有擾流片一側流線到彈體的距離L1明顯大于無擾流片一側的L2,從頭部拖出的流線具有一定的渦量,因此其流過的地方會形成低壓區.左側流線受到噴流的影響在噴流之后發生了流動分離,因此其在彈體中間偏左的較高位置產生了低壓區.而右側的流線恰好處于這個高度,在左側低壓區的影響下向彈體左側流動,使得彈體右側出現大面積高壓區.

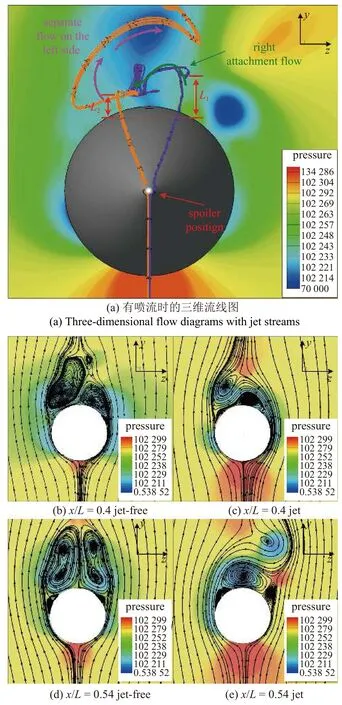
圖14 α=30o時有、無噴流旋成體流線圖Fig.14 Flow line diagram of spinner with and without jets at α=30o

在噴流后方不同截面上的流線圖也可以看出:當無噴流時左右兩側的渦較為對稱,有噴流時右側的渦明顯向左側偏移.如圖15 所示,噴流的存在對彈體側向力系數的分布產生了較大的影響,由于噴流的存在使得噴流周圍及其后方彈體產生了較大的側向力,從而導致了旋成體側向力系數絕對值的增大.無噴流時旋成體背風區表面壓力分布較為對稱,彈體不同橫截面上壓強分布較為對稱,只有在后方出現了小范圍的不對稱,從而產生了一定的側向力.有噴流時由于噴流的影響使得背風區表面壓力分布變的不對稱,彈體表面壓強分布曲線在噴流之前是對稱分布的,在噴流之后受到噴流的影響出現了不對稱分布.

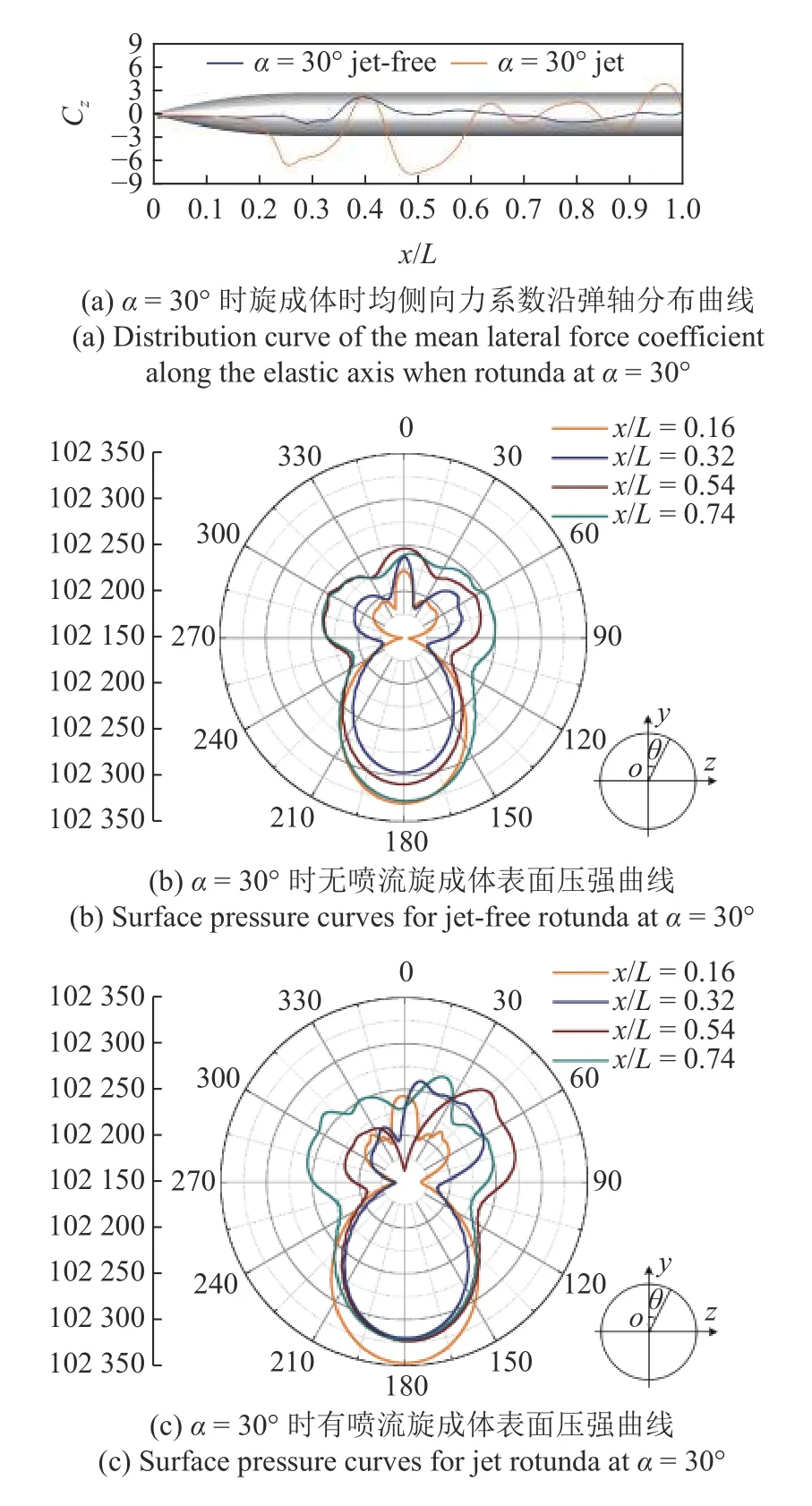
圖15 α=30o時旋成體時均側向力系數沿軸向分布曲線與表面壓強曲線(噴流位于背風區)Fig.15 Average lateral force coefficients along the axial distribution curve and surface pressure clouds when spinning into a body at α=30o(jet stream is located in the leeward area)

2.3.2 噴流位于細長旋成體迎風區

當細長旋成體噴流位于迎風區時其側向力特性與無噴流相比也發生了較大的變化,較為明顯的是當攻角處于20o～40o之間時有噴流旋成體的側向力方向與無噴流時相反.同樣以攻角30o為例,圖16 為噴流位于迎風區時旋成體周圍流線圖.從背風區吹過來的噴流對無擾流片一側的流動產生了較大的影響,使得左側的流動在旋成體前部發生了分離.有擾流片一側的流線有一部分沿著彈體表面流動并未發生流動分離,而沒有擾流片的一側提前發生了流動分離.

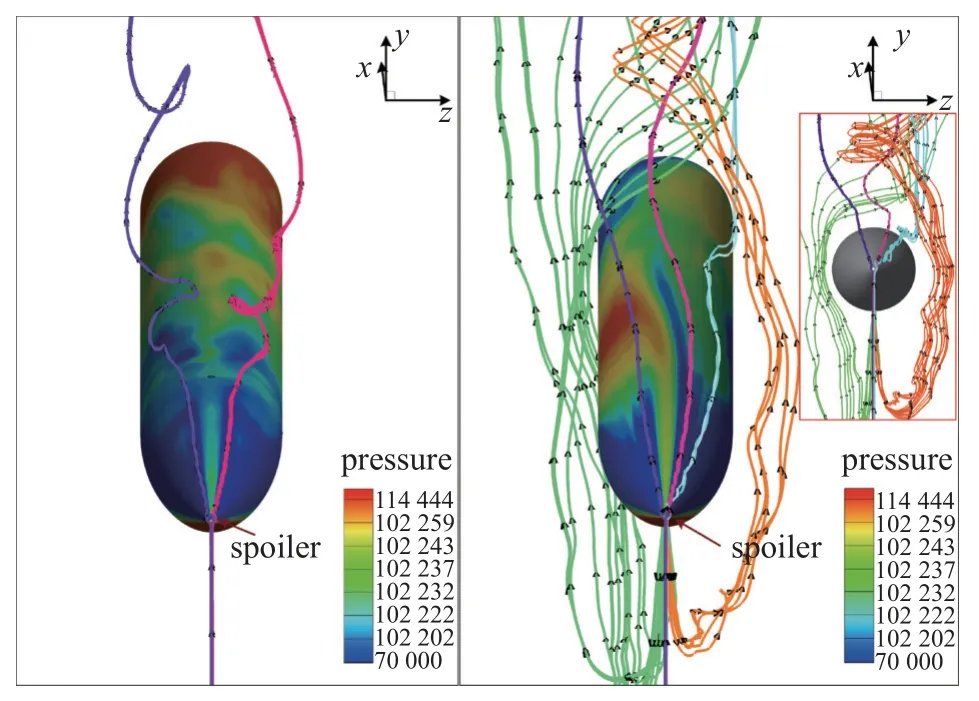
圖16 α=30o時有、無噴流旋成體流線圖(噴流位于迎風區)Fig.16 Flow diagram with and without jet streamline spinning into a body at α=30o (jet stream in windward area)

圖17 為噴流位于迎風區α=30o時旋成體時均側向力系數沿軸向分布曲線與表面壓強曲線,當有噴流存在時彈體中前段部分產生的側向力方向與無噴流時相反,從而導致了側向力方向的改變.從不同截面的表面壓強分布可以發現:當噴流位于迎風區時其對彈體迎風區和背風區表面壓力分布都產生了較大的影響,迎風區和背風區的壓力分布均表現出了非對稱性.而當噴流位于背風區時,其只對旋成體背風區的壓力分布產生了影響.

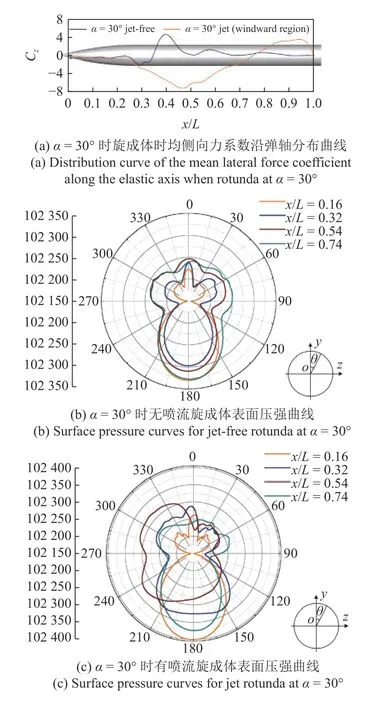
圖17 α=30o時旋成體時均側向力系數沿軸向分布曲線與表面壓強曲線(噴流位于迎風區)Fig.17 Average lateral force coefficients along the axial distribution curve and surface pressure clouds when spinning into a body at α=30o(jet stream is located in the windward area)

圖18 分別給出了細長旋成體無噴流、噴流位于背風區和噴流位于迎風區情況下Q準則等值面示意圖,由于噴流與主流的相互作用使得噴流之后彈體背風區域的流動分離渦發生了變化.無噴流時細長旋成體后方的渦流動較為對稱,從頭部拖出的渦沿彈體兩側向彈尾部發展.當噴流位于背風區域時,從頭部產生的渦在噴口附近受到噴流的影響,z軸負向的渦向z軸正向偏移并擠壓z軸正向的渦,從而使得z軸正向一側的流動首先發生了分離.當噴流位于迎風區域時,噴流與主流首先在彈體的迎風面相互作用,之后在彈體的中后部分沿彈體兩側向背風區發展.此時從頭部拖出的位于z軸正向的渦與迎風區吹來的噴流洗流發生一定程度的卷吸并在噴流洗流的擠壓下向z軸負向移動,從而使得z軸負向一側的流動首先發生了分離.

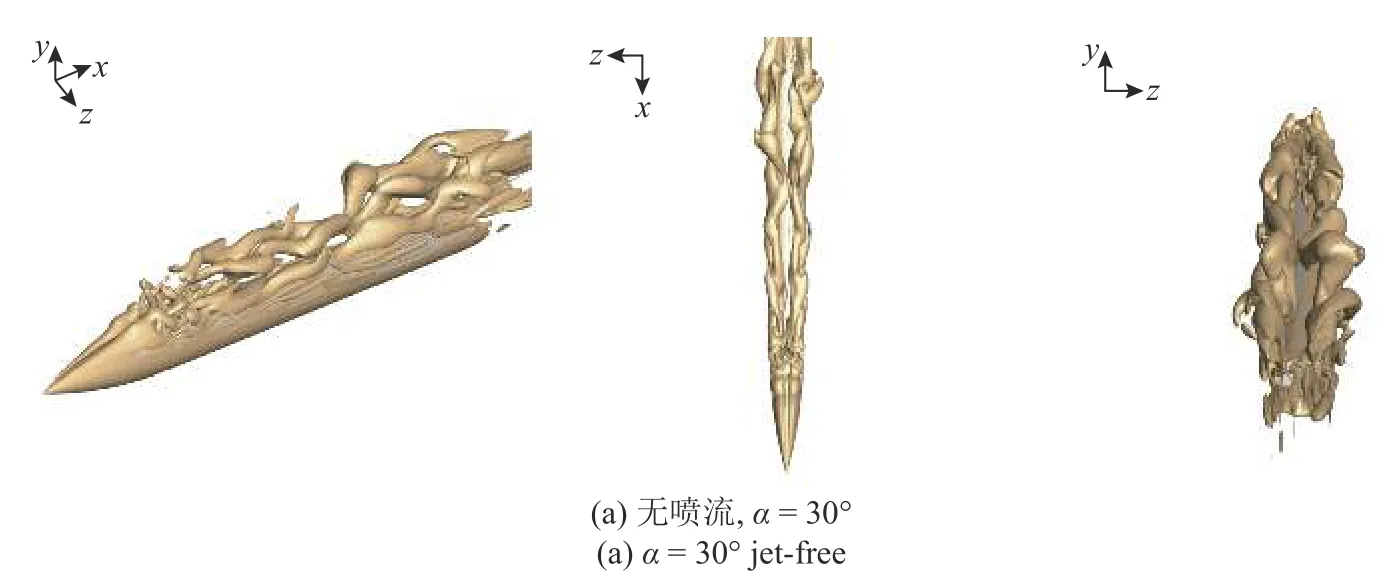
圖18 Q 準則等值面示意圖(Q=7)Fig.18 Iso-surface of Q-criterion (Q=7)

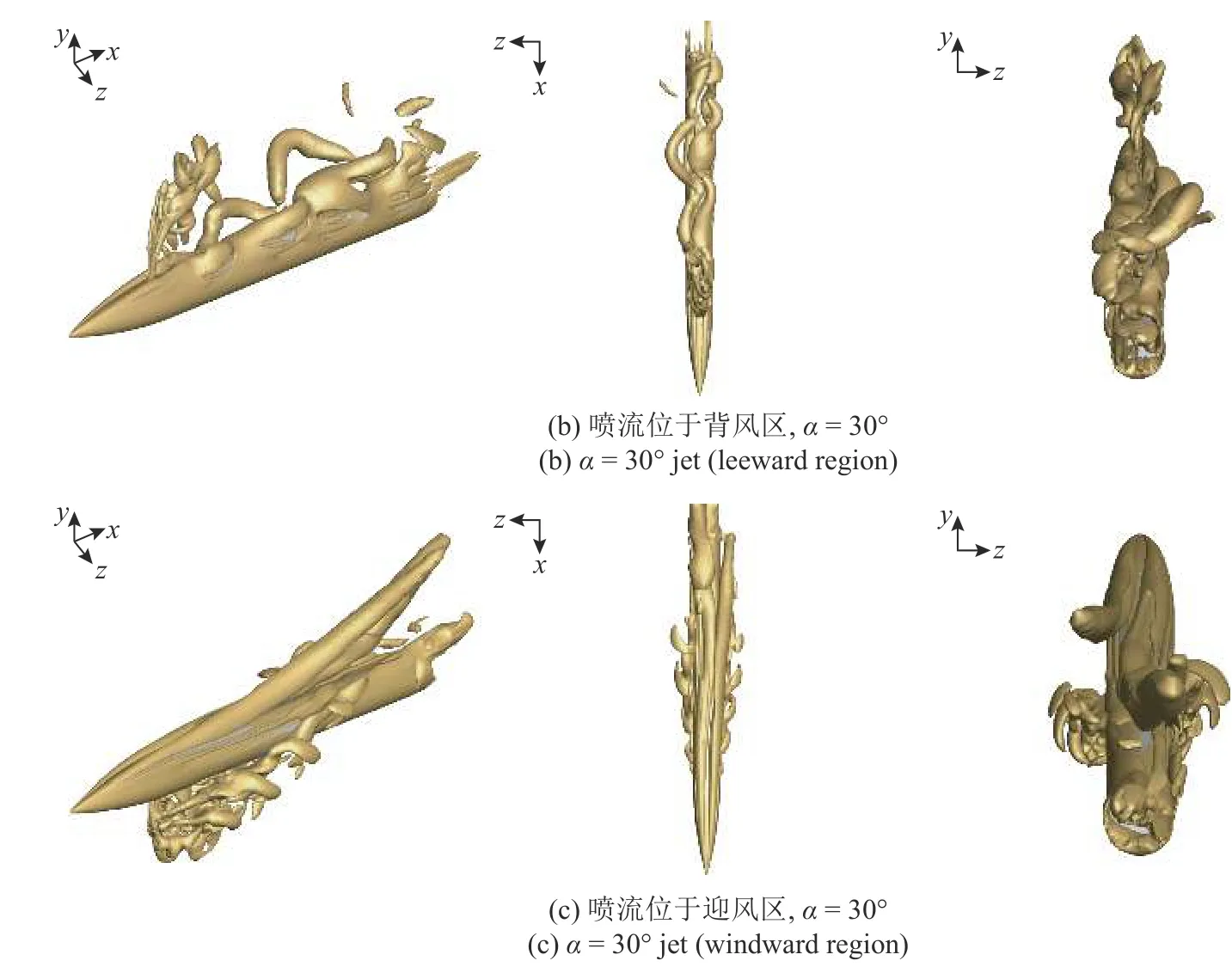
圖18 Q 準則等值面示意圖(Q=7) (續)Fig.18 Iso-surface of Q-criterion (Q=7) (continued)

2.3.3 大攻角下細長旋成體噴流非對稱特性

對于大攻角條件下的細長旋成體,有、無噴流時其非對稱流動分離都較為明顯,因此產生了較大的側向力.圖19 為α=60o時有、無噴流旋成體不同截面處的時均壓強分布圖,由于旋成體的非對稱流動使得旋成體表面時均壓強出現了非對稱分布.當無噴流時彈體前半段不同截面上彈體右側(θ=0o～180o)的壓強要大于彈體左側(θ=180o～360o),因此產生了方向為z軸負向的側向力.但是當有噴流存在時,由于噴流的影響使得彈體表面時均壓力分布出現了一定的變化.當噴流處于迎風區時其對噴口前方的流動產生了較大的影響,使得彈頭部的壓強分布變得更為不對稱,彈體后方的壓強分布與無噴流時相同,都表現出了較為對稱的壓強分布.當噴流處于被風區時,噴流的存在加劇了噴口附近的非對稱特性從而產生了負向的側向力.但是噴流對彈體尾部表面壓強時均分布產生了不同的影響,使得彈體右側(θ=0o～180o)的壓強小于彈體左側(θ=180o～360o),因此產生了方向為z軸正向的側向力,使得旋成體側向力系數絕對值減小.

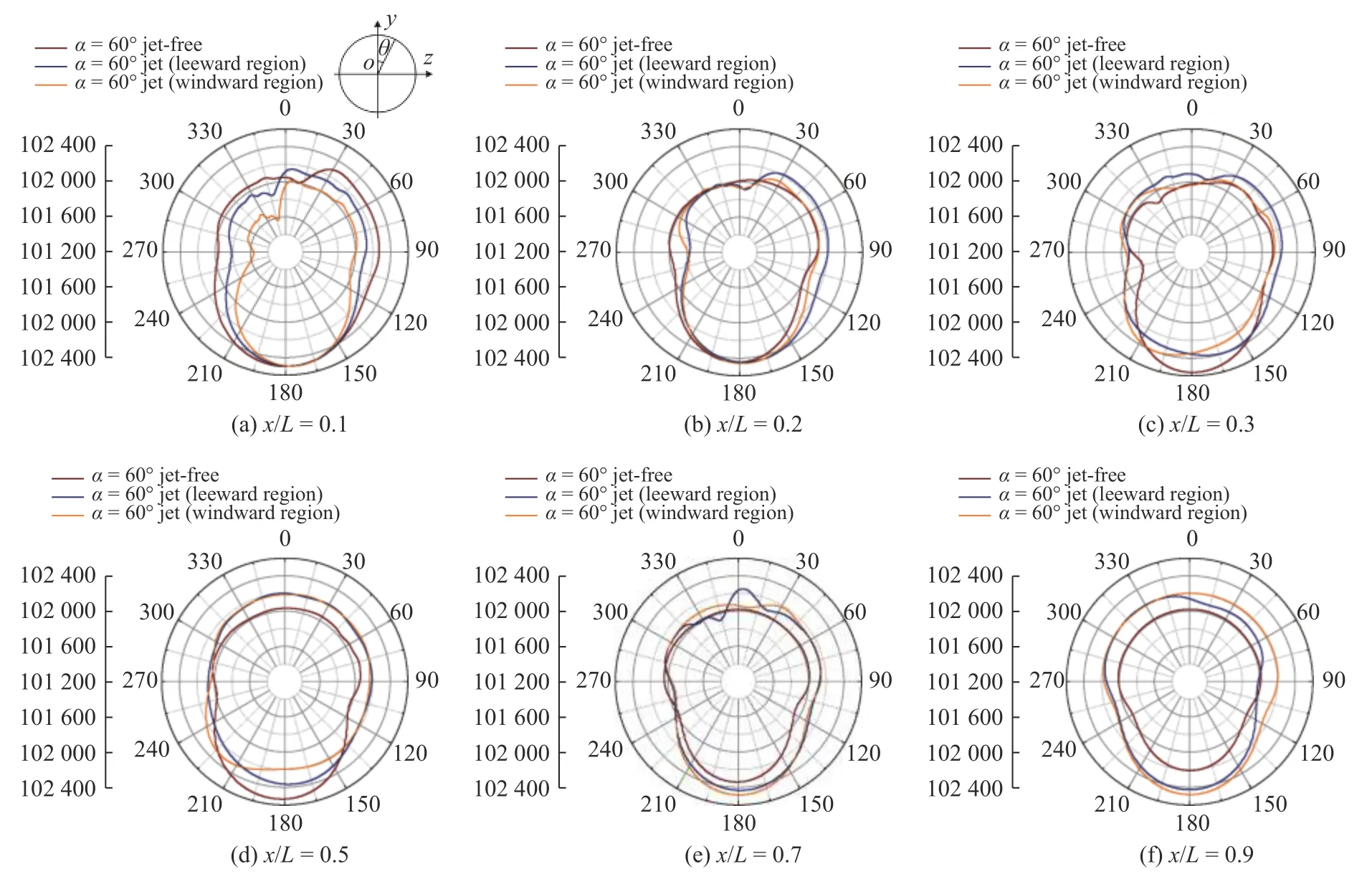
圖19 α=60o時不同截面旋成體表面時均壓強分布曲線Fig.19 Time-averaged pressure curves on the surface of a spinning body with different cross-sections at α=60o

2.3 細長旋成體側向控制數值模擬

當細長旋成體進行側向控制時,由于有沿z軸正向的側向噴流存在,使得其產生沿z軸負向的反作用力.通過分析圖7 中有噴流時的側向力系數可以發現,當攻角在0o～20o之間時旋成體存在較大的側向力,噴流產生的直接力大小為0.5333 N,其產生的側向力系數大小為1.7323,這說明小攻角下的側向力系數是由于噴流的反作用力產生的.當攻角大于50o時旋成體也存在較大的側向力,這是由于大攻角條件下非對稱流動分離和噴流的反作用力兩者共同作用產生的.但是攻角在20o～50o之間時旋成體的側向力較小,甚至在35o時幾乎為0,這說明噴流對彈體產生干擾所導致的氣動力與噴流所產生的直接作用力大小相當、方向相反.

從圖20 中可以看出沒有擾流片的一側流動首先發生了分離,有擾流片的一側后發生流動分離.從表面的壓力云圖可以看出無擾流片一側的流動分離之后旋成體中后部分產生了高壓區,旋成體有擾流片一側由于噴流的影響在彈體噴嘴附近及后方產生了低壓區,從而使彈體產生了沿z軸正向的側向力,這與噴流產生的直接力方向相反、大小相當,從而出現了旋成體攻角在20o～40o之間時旋成體的側向力較小,甚至在35o時幾乎為0 的情況.

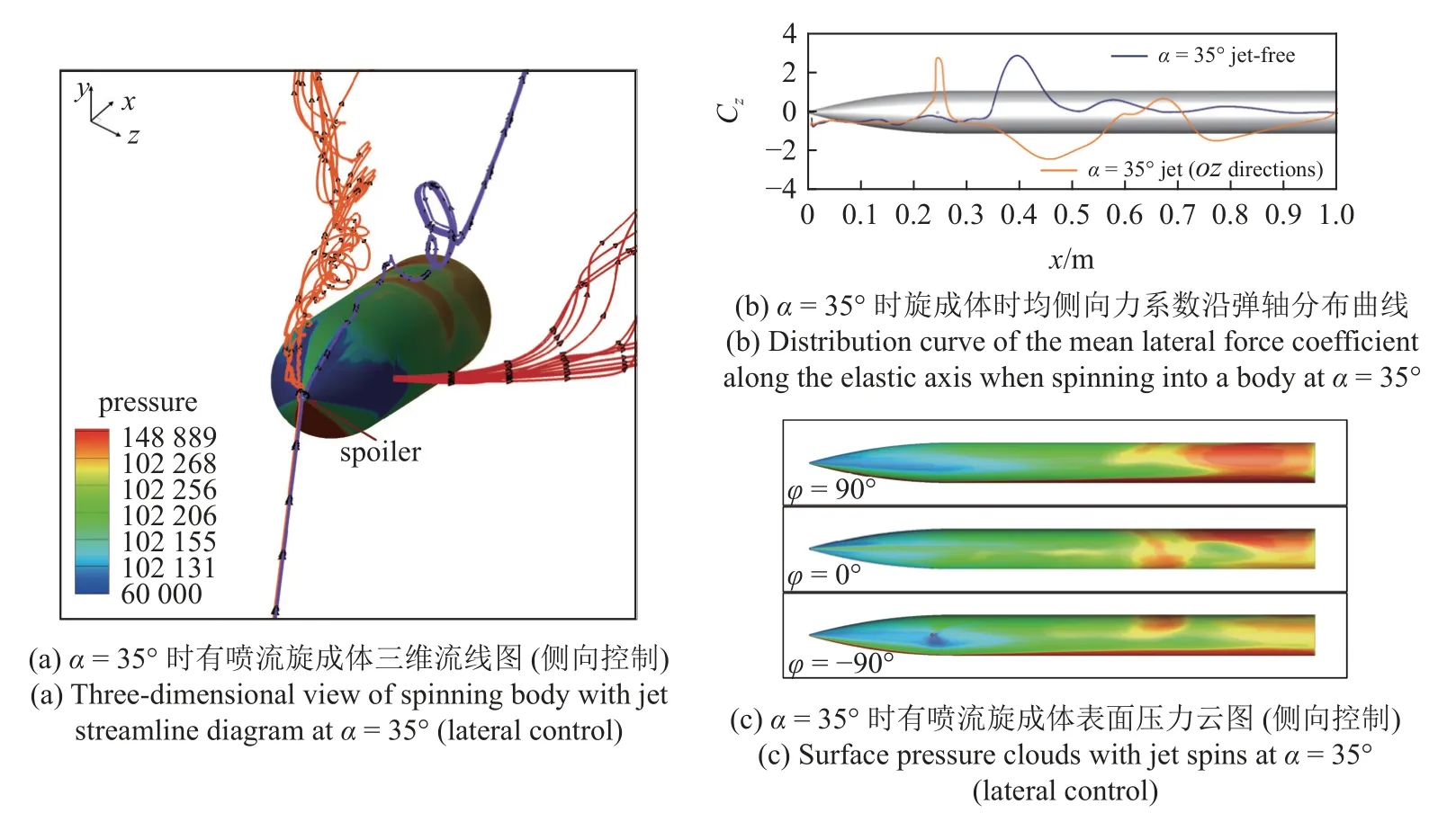
圖20 α=35o時旋成體時均側向力系數沿軸向分布曲線與表面壓力云圖Fig.20 Average lateral force coefficients along the axial distribution curve and surface pressure clouds when spinning into a body at α=35o

圖21 為噴流位于側向時的Q準則等值面示意圖,如圖中A處所示噴流的存在對主流起到了阻擋的效應,在其側后方主流會卷起分離渦(如圖中藍線所示),該分離渦會與頭部拖出的渦相互纏繞使得渦結構發生了變化.如圖中B,C位置所示,B處的渦受到噴流側后方渦的影響與C處的渦表現出了不同的特性.從頭部拖出的z軸正向的渦與噴流側后方卷起的分離渦相互纏繞、卷吸,使得其相比另一側提前破碎成了較多小渦,從而對彈體后方的流動分離、表面壓力分布產生了影響.

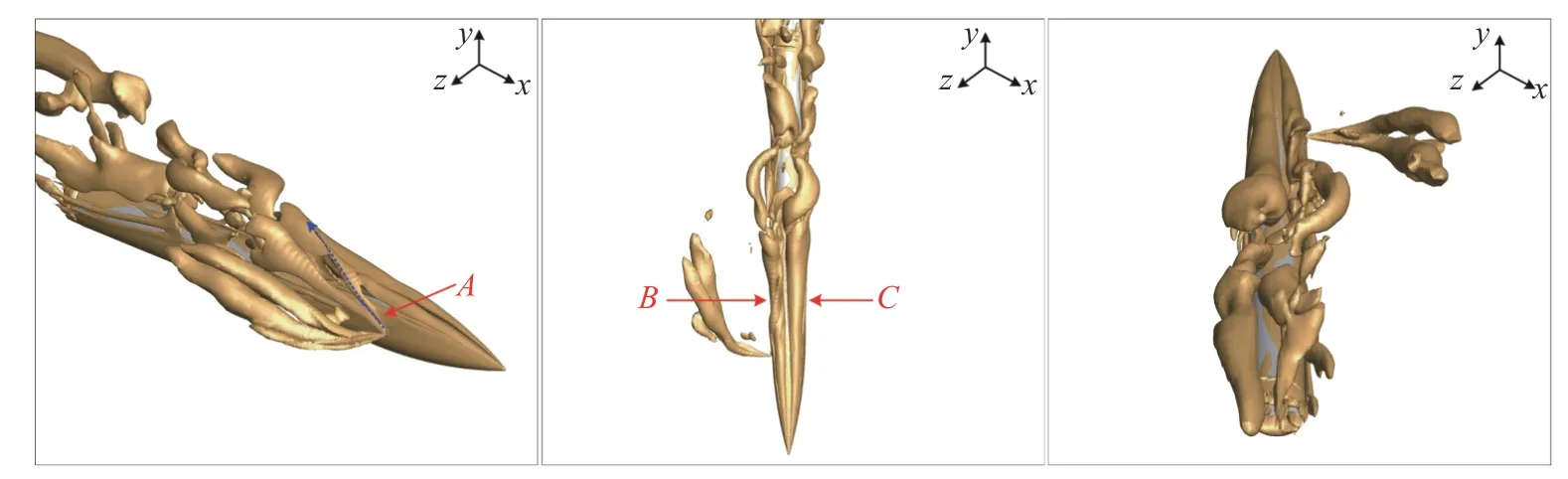
圖21 Q 準則等值面示意圖(Q=7)Fig.21 Iso-surface of Q-criterion (Q=7)

3 結論

本文采用風洞試驗和數值模擬相結合的方法,對雷諾數Re=55000 條件下細長旋成體有、無橫向噴流時大攻角非對稱特性進行了分析.通過風洞試驗發現了旋成體在法向和側向進行噴流時其大攻角非對稱氣動特性與無噴流時的區別,通過數值模擬方法對幾個典型工況下旋成體有、無噴流時的非對稱氣動特性進行了分析,揭示了噴流對旋成體非對稱流動分離的影響,得到了如下結論.

(1)通過風洞試驗發現當細長旋成體進行法向控制時無噴流、噴流位于迎風區和噴流位于背風區的旋成體表現出了不同的非對稱流動特性:首先噴流位于迎風區時攻角范圍在20o～40o之間有噴流和無噴流旋成體所產生的側向力方向相反,攻角大于40o之后側向力系數的方向發生了改變,與無噴流時的側向力系數方向相同,但是其絕對值要比無噴流時的側向力系數小.其次噴流位于背風區時攻角在15o～35o之間有噴流的側向力系數絕對值要明顯比無噴流時大,在隨后的40o～70o之間旋成體側向力系數變化規律與無噴流的趨勢相似.噴流處于背風區時細長旋成體的斯特勞哈爾數普遍要比無噴流時大,噴流處于迎風區時細長旋成體的斯特勞哈爾數普遍要比無噴流時小.

(2)通過風洞試驗發現當細長旋成體進行側向控制時由于沿側向的噴流所產生的直接力使得攻角范圍在0o～20o之間和大于45o時有噴流的旋成體側向力系數絕對值要比無噴流時大,但是攻角在25o～40o之間時旋成體的側向力系數減小,甚至在35o時幾乎為0.有噴流時細長旋成體的斯特勞哈爾數明顯比無噴流時大.

(3)通過數值模擬發現當細長旋成體進行法向控制時,噴流位于迎風區和背風區時噴流都對有擾流片一側的流動分離產生了影響,使得其與無噴流時的流場結構不同.無噴流時細長旋成體有擾流片的一側首先發生流動分離,但是當噴流存在時無擾流片的一側首先發生流動分離,從而導致了側向力絕對值增大以及側向力方向發生改變等現象.

(4)通過數值模擬發現當細長旋成體進行側向控制時,沒有擾流片的一側流動首先發生了分離,有擾流片的一側后發生流動分離.旋成體有擾流片一側由于噴流的影響在彈體噴嘴附近及后方產生了低壓區,無擾流片一側的流動分離之后旋成體中后部分產生了高壓區,使彈體產生了沿z軸正向的側向力,這與噴流產生的直接力方向相反、大小相當,從而出現了旋成體攻角在20o～40o之間側向力較小、甚至在35o時幾乎為0 的情況.