爆轟驅動多介質問題的Lagrange 多分區自適應數值模擬研究1)

周 蕊 李 理 田保林 ,?,

* (北京應用物理與計算數學研究所,北京 100094)

? (北京大學應用物理與技術研究中心,北京 100091)

引言

爆轟波是包含快速化學反應的強間斷面.凝聚炸藥爆轟過程釋放的巨大壓力或能量可以使周圍介質變形、屈服,甚至產生巨大的損傷效應[1-2].因此,凝聚炸藥爆轟在惰性材料約束下的傳播發展過程,及其驅動效應一直是工程應用中被廣泛研究的關鍵問題之一[3-5].目前,對于惰性金屬材料與凝聚炸藥爆轟的相互作用機制認識還存在不足,尤其對于不同約束條件下非理想爆轟過程的規律性認識還有待系統深入地研究[6].

考慮到實驗成本和觀測手段的局限性,多年來數值模擬一直是研究爆轟驅動多介質問題的重要手段.這一問題是典型的爆轟彈塑性多介質大變形問題,模擬該問題的數值方法大概可以分為兩類.一類是歐拉框架下的高精度數值方法[7-12],這類方法的優點是網格固定不動,對大變形問題的適應性強,但存在無法清晰捕捉物質界面,界面附近存在數值耗散等不足.另一類是Lagrange 框架下的數值方法[6,13-14],這類方法因網格跟隨流體自適應運動,可以自然地捕捉物質界面或自由面.特別地,Lagrange 框架下適應多分區的考慮接觸滑移的交錯型數值方法在模擬彈塑性、多介質、薄殼和大空腔等復雜問題時具有獨特的優勢[15-16],成為工程應用中爆轟驅動多介質問題不可或缺的數值模擬手段[17-19].

為了揭示炸藥爆轟和惰性金屬介質相互作用時內部的細致流場結構和演化過程,需要在相當密的網格下開展數值模擬研究.然而,Lagrange 方法在較小的網格尺度下對多介質大變形問題進行數值模擬時,存在因網格畸變導致計算不健壯的問題.在上述問題中,我們主要關注的是爆轟反應區附近及金屬材料中沖擊波附近區域的流場結構和相互作用規律,為了避免整體密網格Lagrange 計算帶來的效率和健壯性困難,發展適應凝聚炸藥爆轟驅動多介質問題的Lagrange 網格自適應方法(adaptive mesh refinement,AMR)是十分必要的.這可以在保障我們關心區域網格分辨率的同時,粗化爆轟波或激波后膨脹區的網格尺度,提升波后大變形區域Lagrange計算的健壯性.

已有AMR 方法多是基于歐拉框架[20],采用分層的結構網格塊自適應加密所關心的流場區域.在歐拉框架下因網格固定不動,不同層網格分別計算后,一般通過時間自適應處理不同層網格邊界之間的銜接,這方面已發展了相對成熟的數值算法.在Lagrange 框架下的AMR 方法研究并不多見,Anderson等[21]曾將歐拉框架下結構網格AMR 方法拓展到Lagrange 框架下,發展了相適應的層間耦合算法.Wang[22]發展了適應復雜材料響應過程的ALE-AMR方法.王瑞利等[23]基于多介質流體力學程序LAD2D發展了非結構網格Lagrange 自適應方法.然而,以上工作都未見在復雜幾何邊界、多分區和多介質問題上的應用.Morrell 等[24-25]基于CORVUS 程序發展了基于cell 的非結構網格自適應方法,實現了跨不同物質區的自適應模擬.然而,他們采用基于“連通數組”的數據結構,這類數據結構與程序緊耦合,不易推廣,且隨著加密層數的增多,程序實現的復雜程度越來越大.

本文針對凝聚炸藥爆轟驅動多介質問題精密化模擬需求,提出了一種新的Lagrange 非結構網格多層自適應方法,及其與接觸滑移的自適應耦合算法,實現了彈塑性、多介質和多分區問題的Lagrange 自適應數值模擬能力.該方法既發揮了非結構網格分層數據結構的靈活性優勢,也通過將有效網格壓至一層進行Lagrange 計算,避免了傳統AMR 中不同層級網格分別計算帶來的層間耦合困難.采用該方法開展了拐角爆轟、多層炸藥隔爆和有限尺寸彎道爆轟等復雜問題的數值模擬研究.計算結果顯示,在保障爆轟波、激波附近網格分辨率的前提下,該模擬方法可大幅縮減可計算網格規模,提升Lagrange計算的健壯性,獲得了豐富的凝聚炸藥爆轟與惰性金屬材料相互作用的流場信息,可為揭示其中的相互作用規律提供豐富的定量數據.

1 適應多分區的Lagrange 非結構網格多層自適應方法

本文基于二維爆轟彈塑性流體力學Lagrange 程序發展非結構網格多層自適應方法,基礎算法的具體細節可參考文獻[13,26].該程序的主要控制方程是考慮彈塑性[27]和復雜狀態方程的流體力學守恒方程組,具體形式如下

其中 β=1 為平面問題,β=0 為以z方向為對稱軸的軸對稱問題.ρ 和e分別代表密度和比內能.vr和vz分別是r方向和z方向的速度.σrr,σzz,σθθ和σrz是Cauchy 應力張量.τ 是偏應力張量,應力與偏應力滿足如下關系

式中 τ 由以下本夠方程求得,壓力p由狀態方程求得.

為了使方程系統封閉,需要引入不同材料的狀態方程,本文凝聚炸藥采用JWL 狀態方程[28].其中未反應炸藥的狀態方程形式如下

炸藥爆轟反應產物的狀態方程形式如下

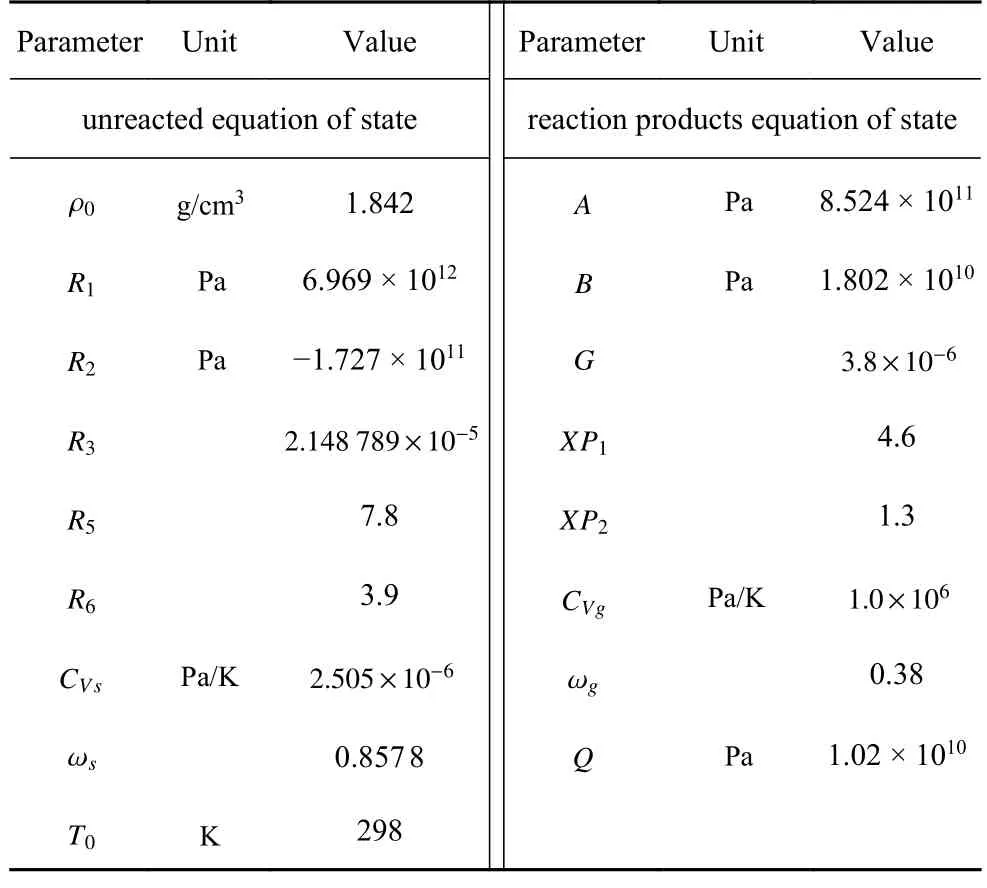
表1 炸藥狀態方程參數取值Table 1 The equation of state parameters for high-explosive

凝聚炸藥爆轟反應過程用Lee-Tarver 三項式反應率模型,具體形式如下

其中 λ 為炸藥的反應份額,λ=0 時代表未反應炸藥,λ=1時代表爆轟產物.式中的I,b,a,x,G1,c,d,y,G2,e,g,z為反應率模型參數.本文計算所用的炸藥反應率模型參數取值如表2 所示.

表2 炸藥Lee-Tarver 三項式反應率模型參數取值Table 2 The Lee-Tarver parameters for high-explosive

其中e為比內能,a0,s,Γ0為狀態方程參數.本文數值算例涉及的金屬材料包括鋼和鋁,它們的狀態方程參數取值如表3 所示.

表3 金屬材料 M ie-Grneisen 狀態方程參數取值Table 3 The M ie-Grneisen equation of state for steel and aluminium

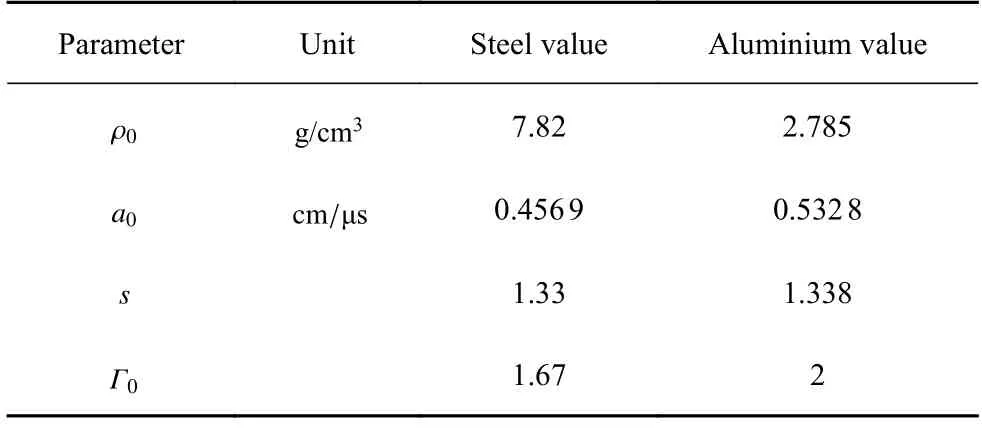
表3 金屬材料 M ie-Grneisen 狀態方程參數取值Table 3 The M ie-Grneisen equation of state for steel and aluminium

上述控制方程的離散基于交錯型Lagrange 格式,詳細的離散過程可參考文獻[26],篇幅原因,本文不再贅述.所有的熱力學量定義在單元中心上,例如 ρ,τ,p,e等;速度v定義在網格節點上.在Lagrange計算中,每一個單元的質量是守恒的,單元密度由初始質量除以當前體積求得.動量方程采用基于面格式的有限元方法離散,內能方程基于有限體積格式離散.在上述方法體系下,需要引入人為黏性捕捉激波間斷,使得人為黏性耗散產生的熵增等于激波引起的物理熵增,以此來達到正確模擬激波波前和波后狀態關系的目的.本文采用文獻[26]中人為黏性形式,具體形式如下

其中,二維問題中l=為網格的特征尺度,A為網格面積,為應變率張量,a為聲速.C0和C1為無量綱參數,在本文的算例中取值分別為1.5 和0.06.

為了適應多分區多介質問題,采用接觸滑移算法處理不同物質之間的相互作用.本文采用基于分配參數思想的接觸滑移算法[29-30],它可以處理接觸后兩接觸面具有相對切向滑移、由分開到接觸、由接觸到分開等復雜情況的問題.這類方法在我們關心的多介質大變形相關工程問題中被廣泛應用.

自適應數據結構的構建和層間耦合策略是自適應方法的核心.此外,考慮到我們關心的問題是多介質、多分區的,網格自適應與接觸滑移的耦合算法也是本研究需要解決的關鍵問題之一.下邊將分別介紹這些內容.

1.1 非結構數據結構及加密準則

非結構多層數據結構是實現Lagrange 多層AMR 的重要基礎.在這個數據結構中,我們設計了“單元類”、“邊類”、“節點類”等自定義數據類型.

(1) “單元類”中提供單元相關的幾何信息、物理量信息、自適應信息,如表4 所示.具體如下.

表4 “單元類”中定義的變量及其物理含義Table 4 The variables and their meanings in “cell type”

①單元幾何信息:單元在當前網格層上的非結構標識號cell_ID;組成單元的節點在當前網格層上的標識號cell_point(1:N_Point),其中N_point 為組成單元的節點數,本文取值為4;組成單元的邊在當前網格層上的標識號cell_edge(1:N_edge),其中N_edge 為組成單元的邊數,本文取值為4;共邊單元在當前網格層上的標識號sameedge_cell(1:N_edge).

②單元物理量信息:材料標識mat;自適應加密準則用到的單元量,例如壓力pressure、密度density、壓力梯度P_grad、密度梯度ρ_grad、爆轟反應份額fac 等.

③單元自適應信息:在當前網格層上單元即將被加密的層數level;父單元在其所屬網格層上的局部單元標識號father_cell;子單元在下一網格層上的局部單元標識號son_cell(1:4),如果當前網格層上單元被加密,那么相應單元將一分為4,形成4 個小單元加入到下一網格層中.

(2) “邊類”中提供與邊相關的幾何信息和自適應信息,如表5 所示.具體如下.

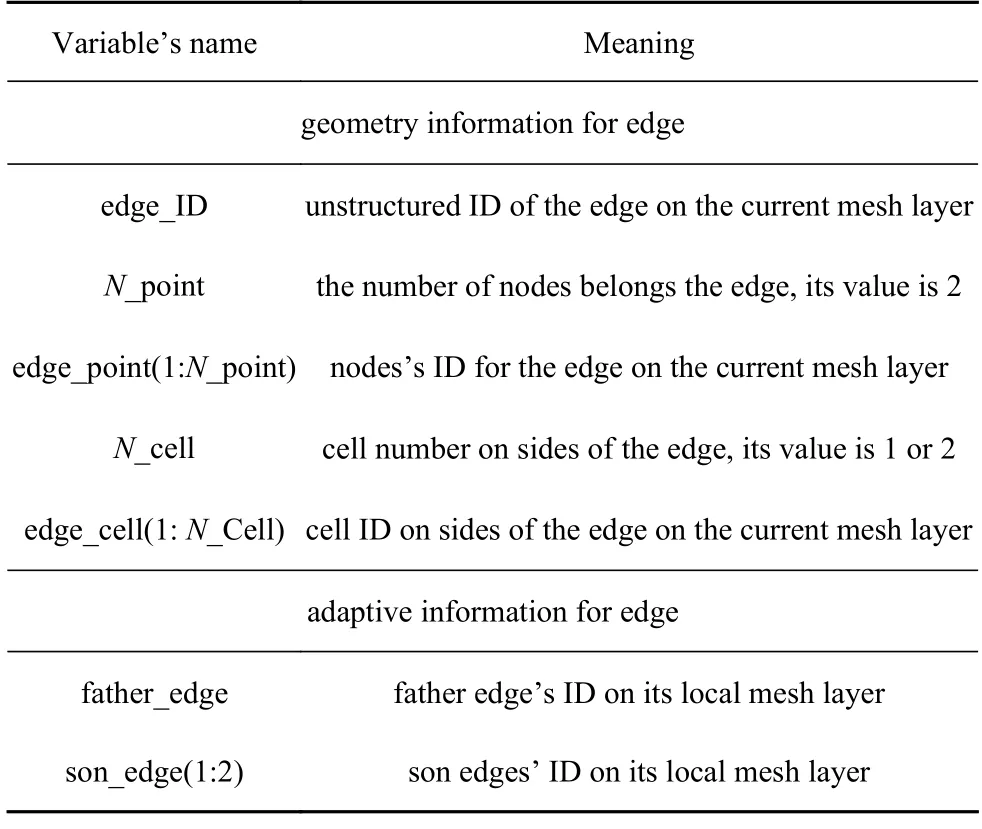
表5 “邊類”中定義的變量及其物理含義Table 5 The variables and their meanings in “edge type”

①邊幾何信息:邊在當前網格層上的非結構標識號edge_ID;組成邊的節點在當前網格層上的標識號edge_point(1:N_point),其中N_point 為組成邊的節點數,本文取值為2;邊兩側單元在當前網格層上的標識號edge_cell(1:N_cell),其中N_cell 為邊兩側的單元數,如果邊是計算的邊界,那么N_cell 取值為1,否則取值為2.

②邊自適應信息:父邊在其所屬網格層上的局部標識號father_edge;如果邊所在的單元被加密,子邊在下一層網格上的局部標識號son_edge(1:2).

(3) “節點類”中提供與網格節點相關的幾何信息、物理量信息和自適應信息,如表6 所示.具體如下.

表6 “節點類”中定義的變量及其物理含義Table 6 The variables and their meanings in “node type”

①節點幾何信息:節點在當前網格層上的非結構標識號node_ID;節點周圍的單元在當前網格層上的標識號node_cell(1:N_cell),其中N_cell 為節點周圍的單元數量,取值在1～4 之間;節點相連的邊在當前網格層上的標識號node_edge(1:N_edge),其中N_edge 為與節點相連的邊的個數,取值為2 或4.

②節點物理量信息:節點位置node_r,node_z;節點邊界條件標識node_boundarycondition,存在3 種類型,0 代表自由邊界,1 代表r方向約束,2 代表z方向約束,3 代表固定不動,4 代表滑移邊界.

③節點自適應信息:對應上一網格層上的節點局部標識號father_node;對應下一網格層上的節點局部標識號son_node.如果當前層節點在上一層或下一層網格上沒有對應的節點,那么對應節點標識號為0.

以上數據結構是普適且獨立的,它不依賴于程序底層和數值算法.根據物理需求,我們首先確定基礎層網格,它可以是整個計算域的網格,也可以是其中的一部分.將基礎層網格信息裝配到上述非結構數據結構中,根據物理過程特點,確定每個基礎層單元的加密層數.對于凝聚炸藥區,我們一般采用反應份額作為網格加密判據;對于金屬材料區,我們采用密度梯度或壓力梯度作為網格加密判據.首先,我們設置最高加密層數為L,通過加密判據先確定基礎層網格上加密層數為L的單元.舉例來說,對于炸藥區,我們將反應份額大于0.01,小于0.99 的單元加密層級標識為L.隨后,通過非結構數據結構中的“單元類”中的共邊單元信息,確定加密L-1 層的單元.以此類推,直到加密層級為1 的單元確定完成為止.因此,所有基礎層網格上的單元加密與否,以及加密層數被確定.在上述加密策略中,相鄰基礎層單元的加密層級最多相差一層,這個約束條件對于后文中的層間耦合是非常重要的.

為了便于理解,我們給出一個簡單的示例來更清楚地解釋基礎層網格單元加密層級確定的過程.如圖1 所示,在一個方形平面計算域中,初始時刻在原點附近給定一個高壓,形成散心爆轟波向外傳播.在某時刻,基礎層網格上的反應份額分布如圖1 所示,我們將反應份額在0.01～0.99 之間的單元加密層級確定為3 層,由此確定了如圖2 左圖所示的紅色單元的加密層級為3.根據基礎層網格上紅色單元的共邊單元信息,確定了如圖2 中間圖所示的綠色單元加密層級為2.進一步地,由綠色單元的共邊單元信息,確定了如圖2 右圖所示的藍色單元加密層級為1.至此,確定了基礎層網格上所有單元的加密層級.

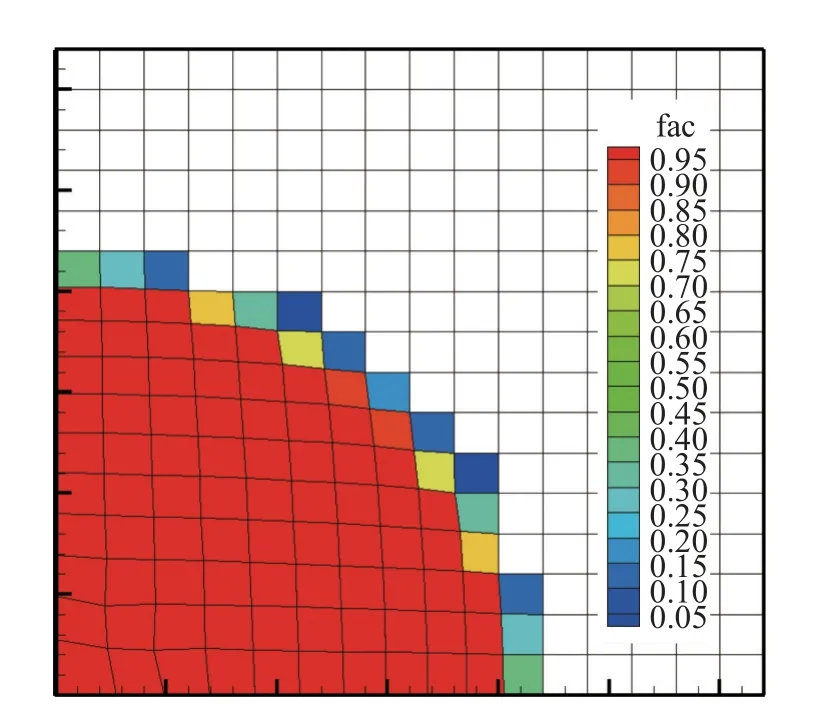
圖1 基礎層網格及爆轟反應份額分布(僅顯示了反應份額大于0.01 的單元)Fig.1 Basic coarse mesh and its reactive variable distribution

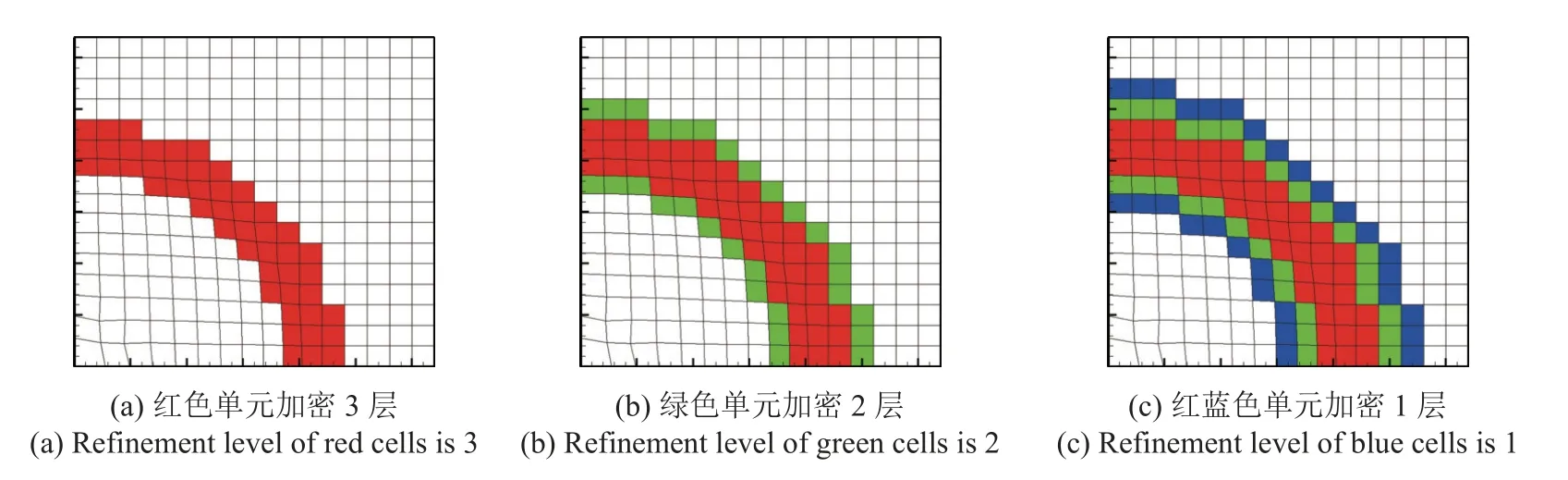
圖2 基礎層網格上單元加密層級Fig.2 Refinement levels of the basic coarse cells

在非結構多層數據結構中,第0 層網格信息與基礎層網格信息一致.按照前述過程確定了第0 層網格上每個單元的加密層級.如圖3 網格細分過程示意圖所示,假設第0 層網格上的4 個單元C0_1,C0_2,C0_3,C0_4 加密層級分別為3,1,2,0.對于單元C0_4 不存在子單元,不會出現在下一層網格信息中.第一層網格數據信息的構建以第0 層數據信息為基礎,在第0 層網格上,如果單元在當前網格層上的加密層級不小于1,那么這個單元被細分為4 個小單元,這4 個小單元加入到第1 層網格數據信息中.在第1 層網格上,所有被0 層網格細分后的小單元都有一個局部標識號,如圖3 中第一層網格上單元C1_1,···,C1_12.這12 個單元在當前網格層上的加密層級等于父單元的加密層級減1,即C1_1,···,C1_4 這4 個單元在第一層網格上的局部加密層級為2,C1_5,···,C1_8 這4 個單元在第一層網格上的局部加密層級為0,C1_9,···,C1_12 這4 個單元在第一層網格上的局部加密層級為1.按照這個思路,就完成了第一層網格非結構數據信息的構建.同樣地,基于第1 層網格的非結構數據信息,如果單元當前加密層級不小于1,那么這個單元被細分為4 個小單元,這4 個小單元加入到第2 層數據信息中,如圖3中第2 層網格上的單元C2_1,···,C2_32.這32 個單元在當前網格層上的加密層級等于父單元的加密層級減1,即C2_1,···,C2_16 這16 個單元在第2 層網格上的局部加密層級為1,C2_16,···,C2_32 這16 個單元在第二層網格上的局部加密層級為0.這樣就構建了第二層網格上的非結構數據信息.以此類推,基于第2 層網格的非結構數據信息,如果單元當前加密層級不小于1,那么這個單元被細分為4 個小單元,這4 個小單元加入到第3 層數據信息中.如圖3中第3 層網格上的單元C3_1,···,C3_64.

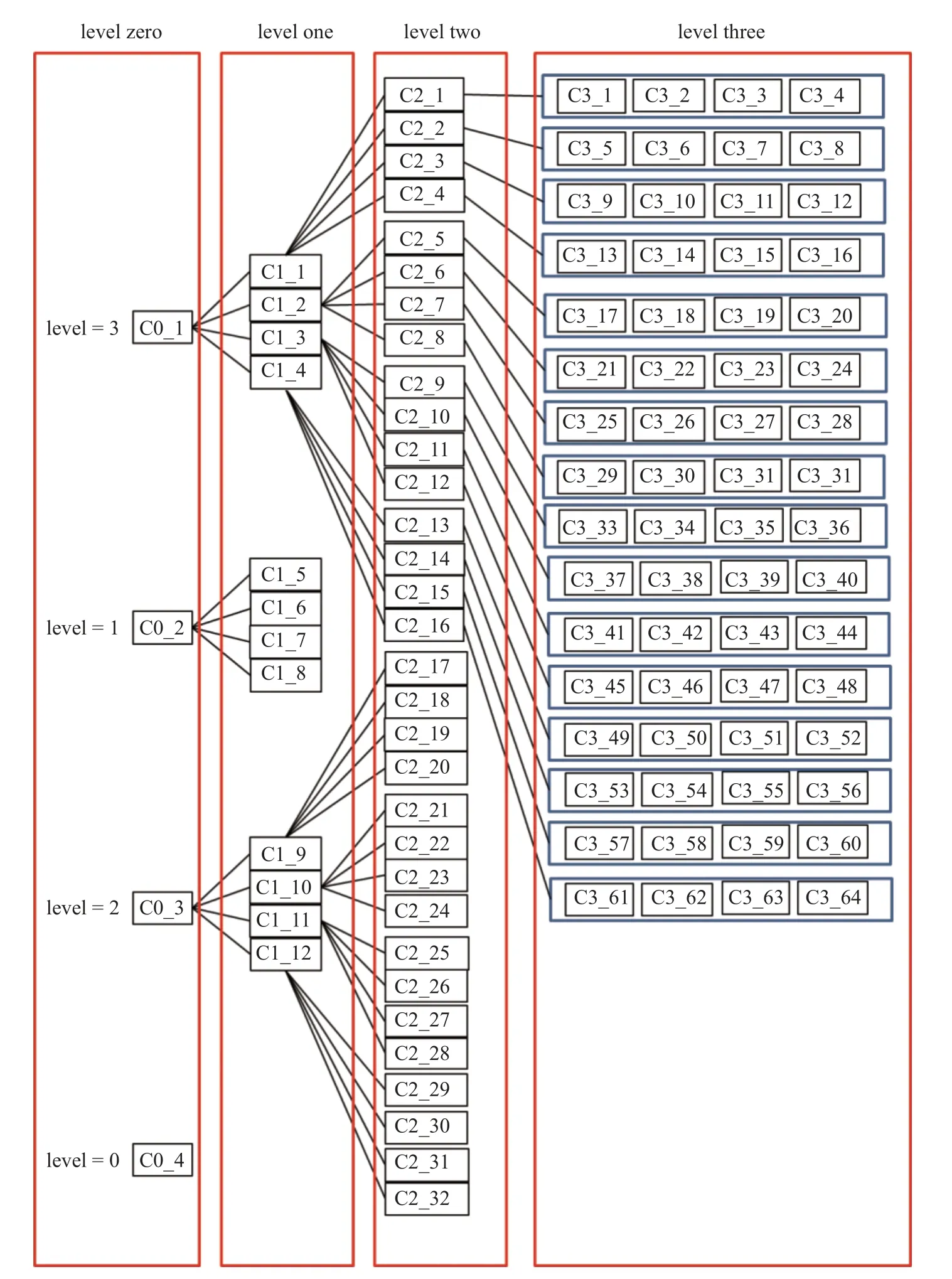
圖3 網格細分過程示意圖Fig.3 Schematic diagram of mesh subdivision progress

按照上述網格細分過程,在每一層網格上都形成了當前層的“單元類”、“邊類”、“節點類”信息,因此,當前層上局部單元-邊(cell_edge)、單元-節點(cell_point)、共邊單元(sameedge_cell);邊-單元(edge_cell)、邊-節點(edge_point);節點-單元(node_cell)、節點-邊(node_edge)等幾何信息被構建.此外,相鄰網格層之間的連通信息也被構建,例如單元-子單元(son_cell(1:4))、單元-父單元(father_cell)、邊-子邊(son_edge(1:2))、邊-父邊(father_edge)、點-上一層節點(father_node)、點-下一層節點(son_node)等.圖1 所示算例按照上述過程,形成了非結構分層網格信息如圖4 所示.

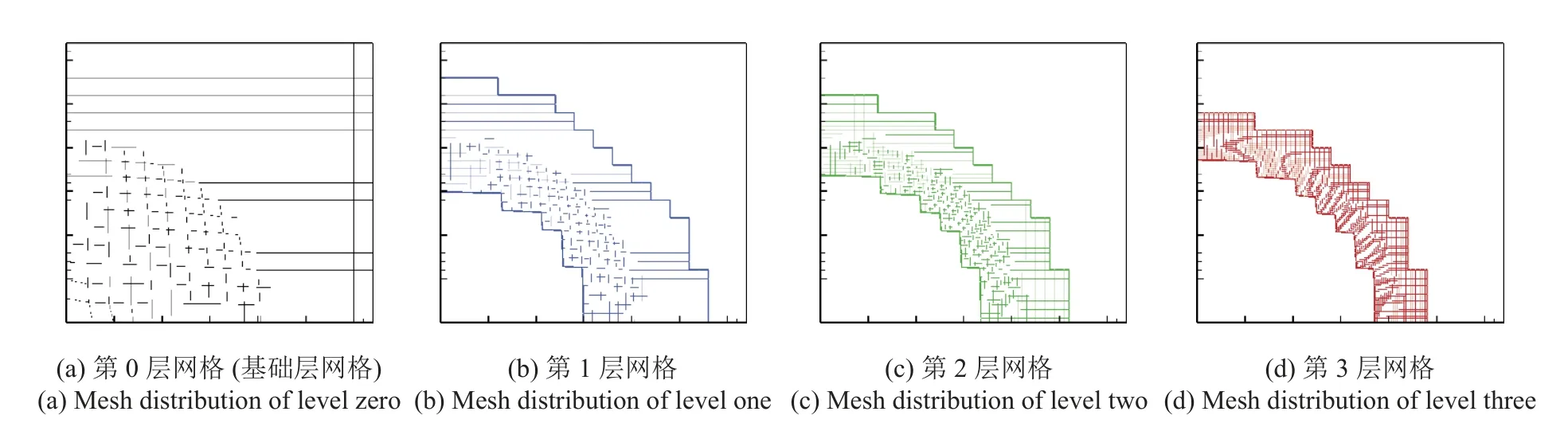
圖4 非結構分層網格信息Fig.4 Unstructured hierarchical mesh information

1.2 層間耦合方法

在傳統的AMR 方法中,在每一層網格上分別進行求解,通過相鄰層之間的邊界條件處理不同層級網格之間的耦合.這類方法在網格固定不動的歐拉框架下是相對成熟和完善的[20].在Lagrange 框架下,網格跟隨流體運動,不同層級網格如果分別進行計算,在層間邊界上會涉及復雜的時間和空間雙重自適應,實現起來是相當困難的.本文通過提取不同層級網格之間的連通信息,實現不同層級上有效網格壓至一層進行Lagrange 計算的AMR 策略,避免了Lagrange 分層計算層間耦合的困難.

具體來說,在第0 層網格上(圖3 第1 列),如果單元的當前加密層級為0,那么該單元加入到有效計算單元隊列中,即C0_4 單元加入到有效計算網格中.在第1 層網格上(圖3 第2 列),如果單元在當前層上的局部加密層級為0,那么該單元被加入到有效計算單元隊列中,即C1_5,···,C1_8 單元加入到有效計算網格中.以此類推,圖3 中第3 列的C2_17,···,C2_32 單元,以及第4 列中的C3_1,···,C3_64 單元加入到有效計算網格中.可見,加入擬計算非結構網格中的有效單元都沒有子單元,在當前層有子單元的網格會被下一層子單元所覆蓋.按照上述思路,圖4所示的多層網格中,有效計算網格如圖5(a)所示,不同顏色代表不同層網格提取的有效網格單元,最終用于Lagrange 計算的整體最密非結構網格構建完成,如圖5(b)所示.通過上述過程,實現了多層非結構網格分層存儲,有效網格壓至一層進行Lagrange計算的AMR 策略.

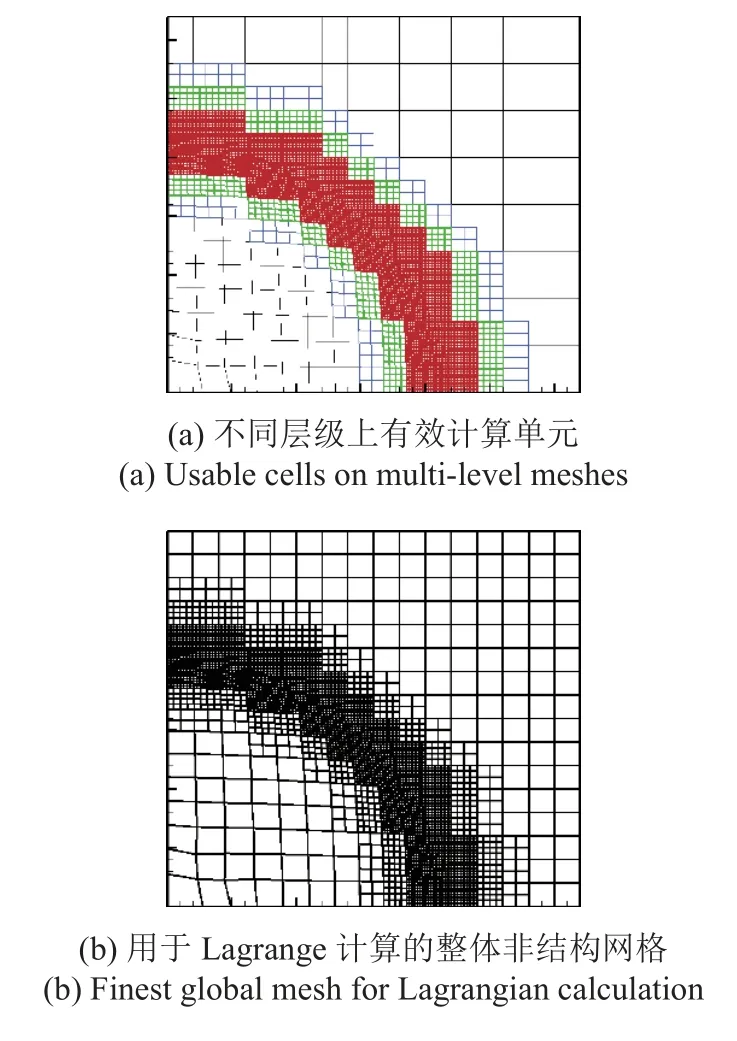
圖5 不同層級上有效網格被壓至一層,形成Lagrange 計算的整體非結構網格Fig.5 Multi-level meshes are flattened onto the final global unstructured mesh

當不同層級網格被壓至一層時,懸點會出現在層間邊界上.在相鄰單元加密層最多相差一層的約束下,網格邊上最多只有1 個懸點,如圖6 所示.本文借鑒文獻[25]中的方法對懸點施加約束.假設懸點為無質量和動量的虛擬點,小單元計算得到的懸點上的節點質量和節點動量按比例分配給相連非懸點節點,懸點的速度和Lagrange 運動位置由相連非懸點節點的速度和位置插值得到.

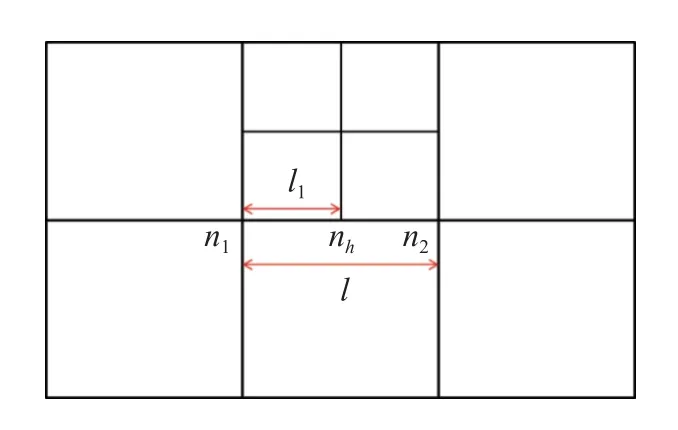
圖6 懸點周圍網格分布示意圖Fig.6 Schematic diagram of mesh distribution around the hang point

具體來說,在圖6 中,節點nh為懸點,節點n1和n2為與nh相連的兩個規則節點.l1為節點n1與節點nh的距離,l為兩個規則節點n1與n2之間的距離.定義比例因子f由下式計算

那么,懸點nh的速度和坐標位置由規則節點n1和n2的速度和坐標位置計算得到,具體形式如下

兩個規則節點的質量和節點力按如下公式進行修正

以上懸點計算方法在文獻[24-25]中被成功應用,該約束方法解決了層間耦合的問題.然而,對于懸點計算方法的深入系統分析還有待后續進一步開展.

1.3 自適應接觸滑移耦合方法

本文采用的接觸滑移算法需要人為事先給定主線和從線,由此得到對應的主點、主單元、從點和從單元.具體計算流程包括:判斷主從點接觸狀態、對符合條件的主點施加接觸約束、計算相互作用后主點的加速度、計算產生碰撞后的主點速度、計算從點的速度和加速度、調整下一步時間步長.在Lagrange 自適應計算的過程中,如果主單元或從單元被自適應加密或粗化,那么滑移線的幾何拓撲勢必會發生改變.本文提出了接觸滑移與Lagrange 自適應算法的“緊耦合”策略.具體來說,在1.1 節中構建的分層非結構數據結構中,在每一層網格上增加滑移線的幾何信息,通過已經構建的不同層級網格之間的連通信息,即能提取出滑移線的單元、節點在相鄰層級上的連通信息.通過提取這些連通信息,可以在形成整體Lagrange 計算非結構密網格的同時,自適應形成新的滑移線幾何拓撲.

圖7 給出了一個示例,計算域中包含兩塊炸藥區,初始時刻在原點附近給定一個高壓,散心爆轟波逐漸向外傳播,從下邊的炸藥區傳至上邊的炸藥區.上邊的炸藥區定義為滑移線的主側,下邊定義為從側.計算到某一時刻,自適應網格分布如圖7(a)所示,圖中藍色線為滑移線所在位置.我們將紅色矩形圍起的區域放大,如圖7(b)和圖7(c)所示.在基礎層網格上,從單元的全局單元編號依次為211,212,213,···,對應主單元的全局單元編號為191,192,193,···,如圖7(b)所示.通過提取和搜索相鄰網格層上的滑移線幾何連通信息,形成新的整體非結構密網格上的滑移線幾何拓撲關系.如圖7(c)所示,新的從單元全局編號依次為184,328,331,540,543,552,555,···,對應的主單元的全局編號為173,325,326,529,530,533,534.

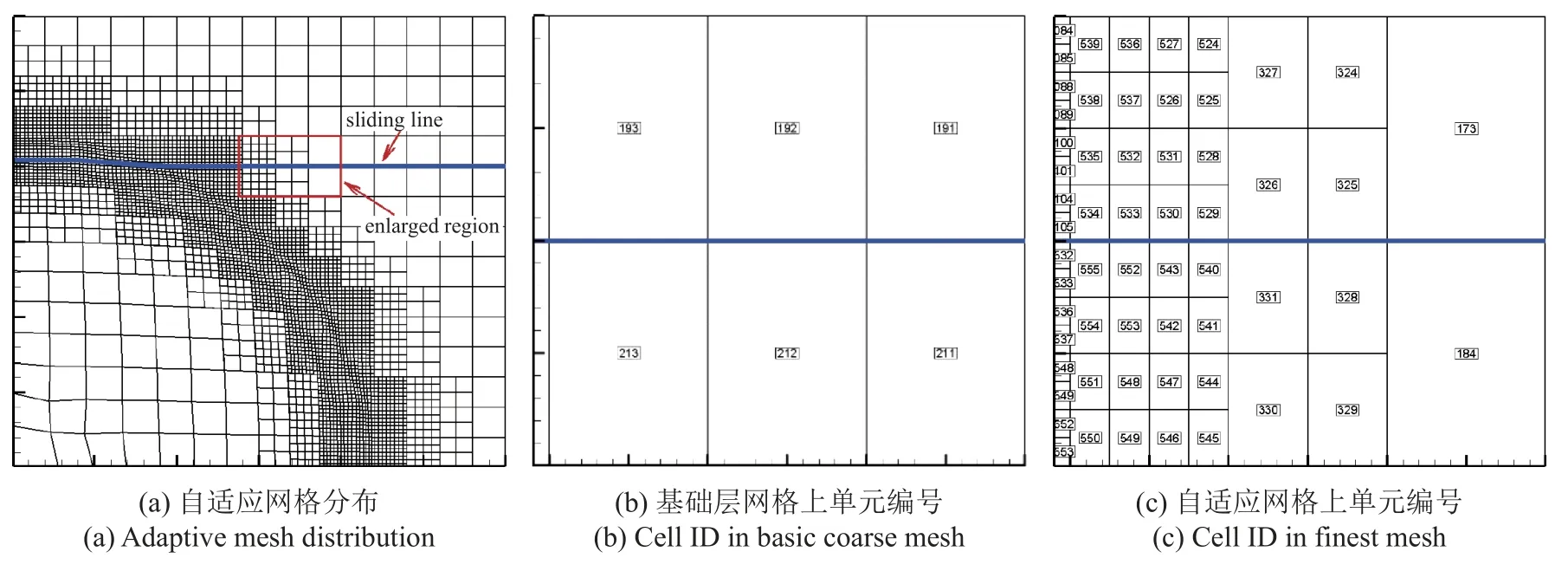
圖7 接觸滑移算法與Lagrange AMR 方法耦合,形成新的接觸滑移幾何拓撲Fig.7 New geometric topology of the sliding interface is rebuilt in the adaptive coupling strategy

1.4 Lagrange 自適應計算流程

完成上述AMR 方法設計的基礎上,按照如圖8所示的流程實現上述AMR 策略與Lagrange 主體算法的耦合.首先,提取用于自適應計算的基礎層網格,將其裝配至非結構自適應數據結構中.然后,根據所關心物理問題的特點確定自適應加密準則,基于此,確定基礎層網格上每個單元的加密層級.隨后,分層構建非結構網格數據信息,得到每一層網格上所有的幾何信息、自適應連通信息以及必要的物理量信息.最后,提取出用于Lagrange 計算的有效非結構網格信息,以及懸點和滑移線信息,將它們傳回給Lagrange 主體算法開展Lagrange 計算.在Lagrange計算的過程中,需要實時監測自適應網格分布是否滿足物理過程特點,根據監測判據開展新的自適應信息的構建.

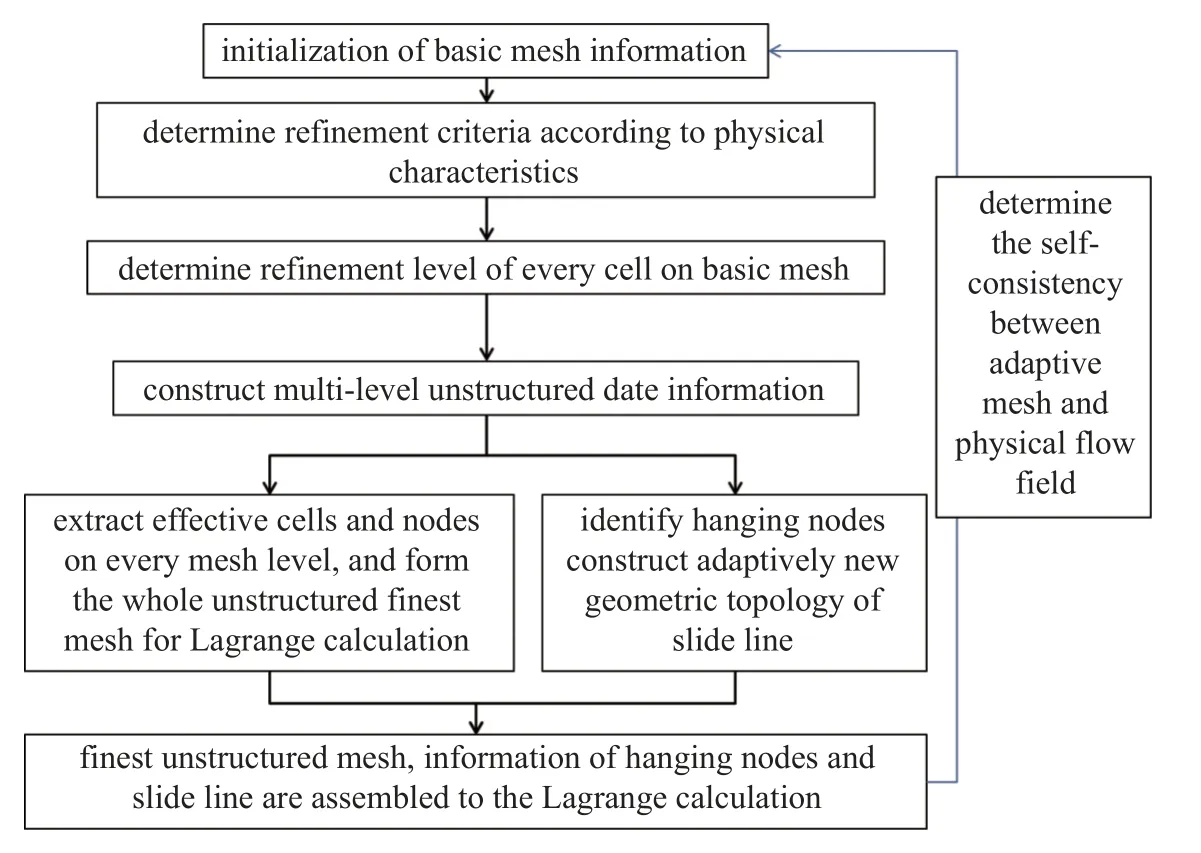
圖8 AMR 與Lagrange 主體算法耦合流程Fig.8 Coupling low between the AMR and Lagrange algorithm

以前文中提到的簡單算例為例,給出自適應網格更新的步驟如下.

(1) 假設自適應計算至某一時間步,Lagrange 計算網格分布如圖9(a)所示,自適應非結構數據結構中存儲了完備的用于計算的非結構網格幾何信息和物理量信息.基于這個密網格,得到對應基礎層網格上的必要物理量.基礎層網格的節點位置由自適應網格上對應節點位置直接賦值得到,物理量由相交重映計算得出.需要強調的是,這個過程中只重映與加密判據相關的物理量即可.例如,對于爆轟問題來說,只重映反應份額即可.基礎層網格上的反應份額分布如圖9(b)所示.

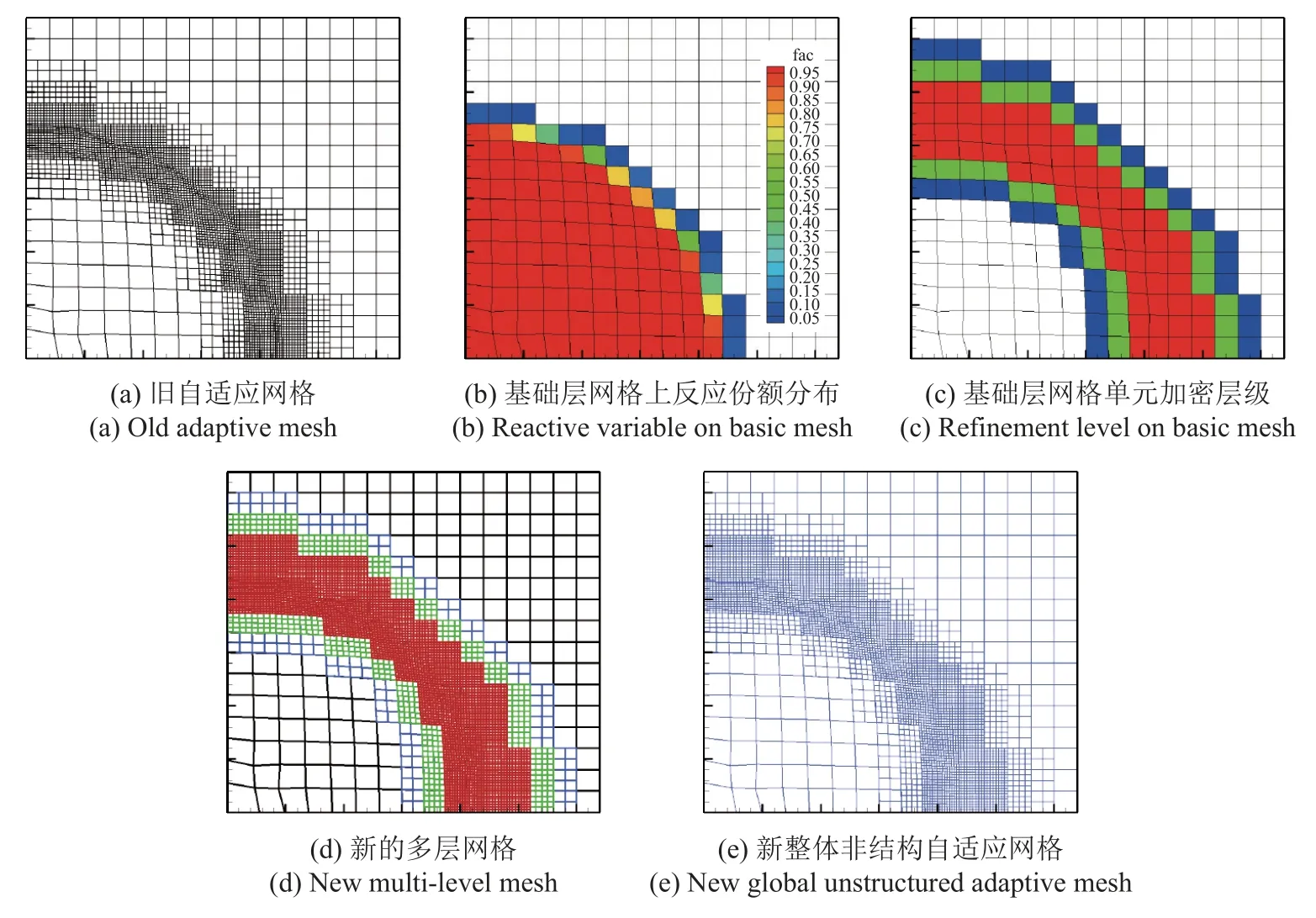
圖9 自適應網格更新流程Fig.9 Update process of adaptive mesh

(2) 根據圖2 所示流程,確定基礎層網格上每個單元是否加密,以及加密層級,如圖9(c)所示.圖中紅色單元加密層級為3,綠色單元加密層級為2,藍色單元加密層級為1.

(3) 按照圖3 所示流程,分層構建非結構數據信息,如圖9(d)所示.由此得到每一網格層上局部幾何拓撲關系,以及相鄰層級之間的自適應連通信息.

(4) 通過提取不同層級之間的連通信息,獲得有效計算非結構密網格的數據信息,新的壓至一層的自適應非結構網格分布如圖9(e)所示.

(5) 通過以上步驟,得到舊自適應網格(圖9(a))的幾何信息和物理量信息,以及新自適應網格(圖9(e))的幾何信息.采用非結構相交重映方法獲得新自適應網格上的物理量信息.

(6) 圖9(e)所示的自適應網格幾何信息和物理量信息傳回給主體程序進行后續的Lagrange 計算.隨后,根據加密判據,返回步驟(1).

2 算例驗證

考慮到采用的爆轟彈塑性流體力學Lagrange程序已經經過多種復雜算例的驗證與確認,對凝聚炸藥爆轟過程的模擬有較高的置信度.例如對于典型PBX9404 炸藥的一維爆轟傳播過程,數值計算得到的穩定爆轟波傳播速度為 0.8817 cm/μs,相同條件下,根據Rayleigh-Hugoniot 關系推導的理論爆轟波傳播速度為 0.8808 cm/μs,可見數值模擬結果與理論解的偏差僅為0.1%.因此,在本節的數值驗證中,一般將一致均勻密網格的數值模擬結果作為基準解,將Lagrange 自適應模擬結果與其定量比較,來說明所提出自適應方法模擬結果的正確性.

我們采用一維爆轟傳播問題考核所提出Lagrange非結構網格多層自適應方法的正確性.圖10 為一維爆轟傳播問題的數值模擬結果.初始時刻,在炸藥左端設置高壓區起爆爆轟波,在爆轟波傳播的過程中,自適應密網格一直跟隨爆轟波陣面移動,使得爆轟反應區附近一直保持預設的網格分辨率.將自適應加密3 層的模擬結果與同程度均勻密網格模擬結果進行定量比較,如圖10 所示,相同時刻爆轟反應區附近的網格分布及壓力分布完全一致.兩種方式計算得到的最大壓力均為36.98 GPa,爆轟波位置均在z=12.5567 cm 處,驗證了Lagrange 自適應模擬方法的正確性.自適應模擬在保證爆轟反應區網格分辨率的前提下,相比于均勻一致加密,節省95%的網格規模.

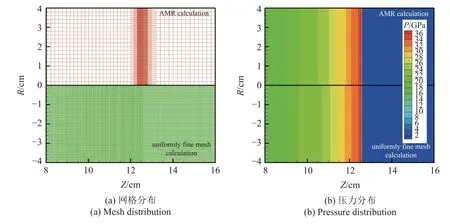
圖10 一維爆轟傳播問題 (上:AMR(加密3 層)計算結果,下:一致密網格計算結果)Fig.10 1D detonation propagation (up:AMR calculation,down:uniformly fine mesh calculation)

為了定量考核Lagrange 多層自適應方法與接觸滑移耦合算法的正確性,我們設計了如圖11 所示的一維爆轟傳播算例.這個算例包括3 個物質區.2 條滑移線、2 種材料,同時還存在滑移線相交的情況.該問題本質上是一維問題,初始時刻,在左側金屬材料鋼區與右側兩塊炸藥之間存在空隙,需采用開穴滑移算法計算.兩塊炸藥之間的滑移線不考慮相對滑動,采用束縛滑移算法計算.初始時刻,在炸藥區左側設置高壓區起爆爆轟波,爆轟產物膨脹會使金屬與炸藥之間的空隙閉合.如圖11 所示,Lagrange自適應方法能正確模擬含復雜滑移線(含相交)情況的算例.圖11(b)和圖11(c)分別為采用自適應方法模擬和同程度均勻密網格模擬的壓力分布,兩種方式模擬在相同時刻的爆轟波位置和爆轟波附近壓力分布定量一致,最大壓力均為36.9548 GPa,爆轟波面位置在z=3.8349 cm 處,驗證了Lagrange 自適應方法與接觸滑移耦合算法的正確性.

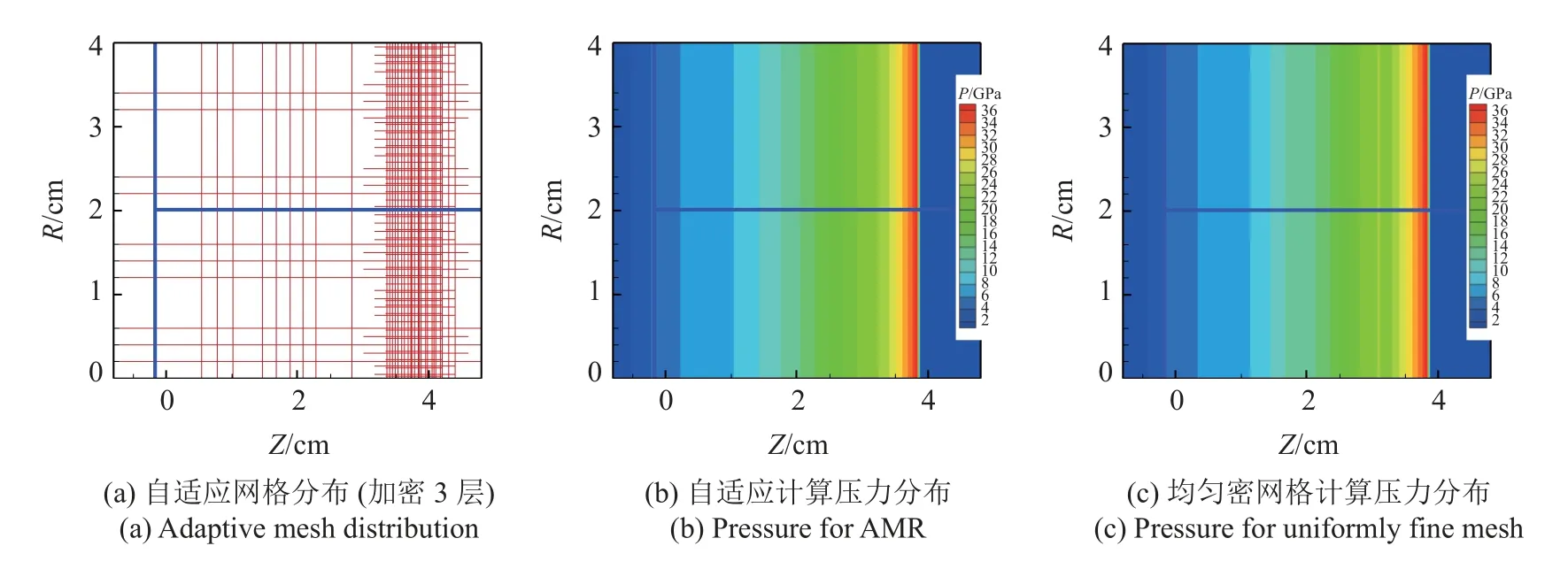
圖11 含多條滑移線的一維爆轟傳播問題,藍色實線為滑移線所在位置Fig.11 1D detonation propagation with slide line,blue solid line is slide line

更進一步地,我們設計了如圖12 所示的二維爆轟傳播與對碰問題,來考察Lagrange 多層自適應方法對于多點起爆、爆轟波對碰等復雜波系結構的適應性.我們分別在兩個角點處設置局部高壓起爆爆轟波,兩道爆轟波相向傳播直至對碰.如圖13 和圖14 所示,在爆轟波傳播與對碰的過程中,自適應密網格有效地跟隨激波運動.隨著兩道爆轟波靠近、對碰,兩塊非結構自適應密網格自動銜接.同時,在相同時刻自適應加密3 層的模擬結果與同程序均勻一致密網格模擬的爆轟波陣面位置和波系結構一致,體現了所發展Lagrange 多層自適應方法對復雜問題的適應性.

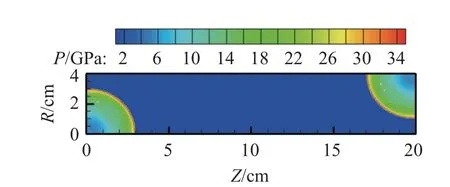
圖12 二維爆轟傳播與對碰問題、壓力分布 (t=3 μs)Fig.12 2D detonation propagation and collision,pressure distribution (t=3 μs)

3 爆轟驅動多介質問題的Lagrange 自適應模擬

本節開展拐角爆轟、多層炸藥隔爆、有限尺寸彎道爆轟等復雜爆轟驅動多介質問題的Lagrange自適應數值模擬研究.

3.1 拐角爆轟問題

本文所模擬的拐角爆轟問題,初始計算域為(0.0,20.0 cm)×(0.0,10.0 cm),其中金屬材料鋼的初始幾何尺寸為(0.0,8.0 cm)×(0.0,6.0 cm),剩下的區域為凝聚炸藥.基礎層網格劃分100×50 個單元,對應網格尺寸為0.2 cm.在這個軸對稱問題中,初始時刻在炸藥區左側設置高壓區域,形成爆轟波遇金屬材料拐角形成復雜的爆轟波繞爆過程.在炸藥中,采用反應份額作為加密判據,當單元反應份額介于0.01～0.99 之間時,單元加密3 層.在金屬材料中,采用密度梯度作為加密判據,當密度梯度大于0.05 時,相應單元加密3 層.自適應加密后,最小網格尺寸為0.25 mm.如圖15 和圖16 所示,自適應計算的密網格始終跟隨爆轟波陣面及金屬中沖擊波移動,有效模擬了爆轟波沿金屬邊界傳播,及遇金屬拐角繞爆的過程.一致密網格模擬得到的爆轟波傳播和繞爆過程與自適應模擬結果一致.自適應計算拐角處節點起跳時間為8.8143 μs,一致密網格計算拐角處節點起跳時間為8.8066 μs,相差小于0.1%.自適應計算中爆轟波附近加密3 層實際計算網格總數不超過3 萬,而同程度一致密網格計算網格總數為32 萬.

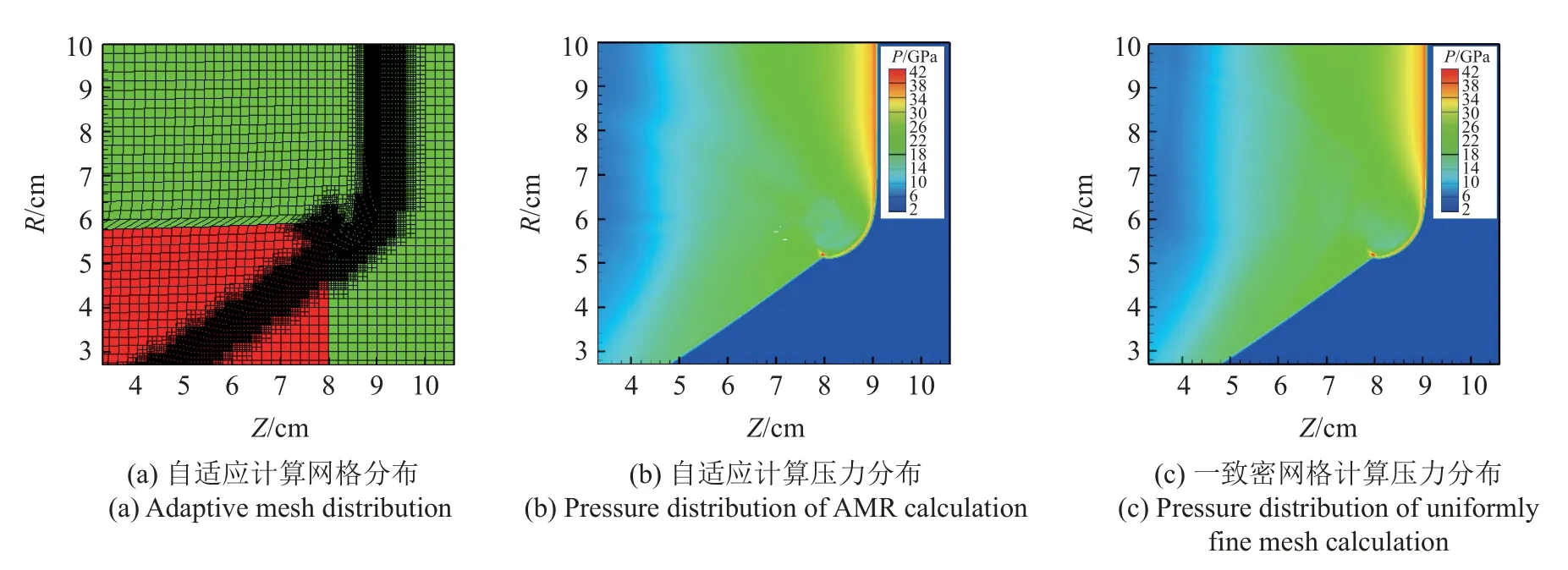
圖16 軸對稱多介質拐角爆轟問題模擬結果 (t=10 μs)Fig.16 Axisymmetric multi-material corner detonation problem (t=10 μs)

3.2 多層炸藥隔爆問題

在實際工程中,除了經常出現爆轟繞爆這一復雜現象,爆轟波過金屬隔爆也是常見現象.為此,設計了如圖17 所示的多分區、多介質問題,這個算例包含4 個物質區、3 條滑移線、3 種材料,存在爆轟波傳播、過金屬隔爆等復雜物理過程.炸藥與金屬之間允許切向移動,接觸滑移計算采用單純滑移算法.兩塊炸藥的初始位置分別為(0.0,20.0 cm)×(0.0,2.0 cm) 和 (0.0,20.0 cm)×(2.4 cm,4.4 cm);兩塊炸藥之間的金屬為鋁,其初始幾何位置為(0.0,20.0 cm)×(2.0 cm,2.4 cm);炸藥外邊界處的金屬為鋼,其初始幾何位置為(0.0,20.0 cm)×(4.4 cm,4.8 cm).初始時刻,在坐標原點附近設置高壓點起爆爆轟波,爆轟波在下方第一塊炸藥中形成散心爆轟向外傳播,驅動中間層金屬材料,壓縮引爆上方第2 塊炸藥,產生隔爆.隨后在兩塊炸藥中形成兩個爆轟波同步向右側傳播.如圖17 和圖18 所示,我們僅在炸藥區采用反應份額作為自適應加密判據,將爆轟波陣面附近網格自適應加密3 層.在整個爆轟傳播發展的過程中,自適應密網格都能有效地捕捉爆轟波所在位置,實現爆轟波陣面附近的高分辨率模擬.自適應加密3 層與同程度均勻密網格模擬的爆轟波陣面附近壓力分布是一致的,驗證了該Lagrange 多層自適應方法對復雜問題的適應性.在這個問題中,自適應模擬最大網格規模為1.3 萬,同程度均勻密網格模擬網格規模為12.84 萬,可見自適應模擬節省了90%以上的計算量.

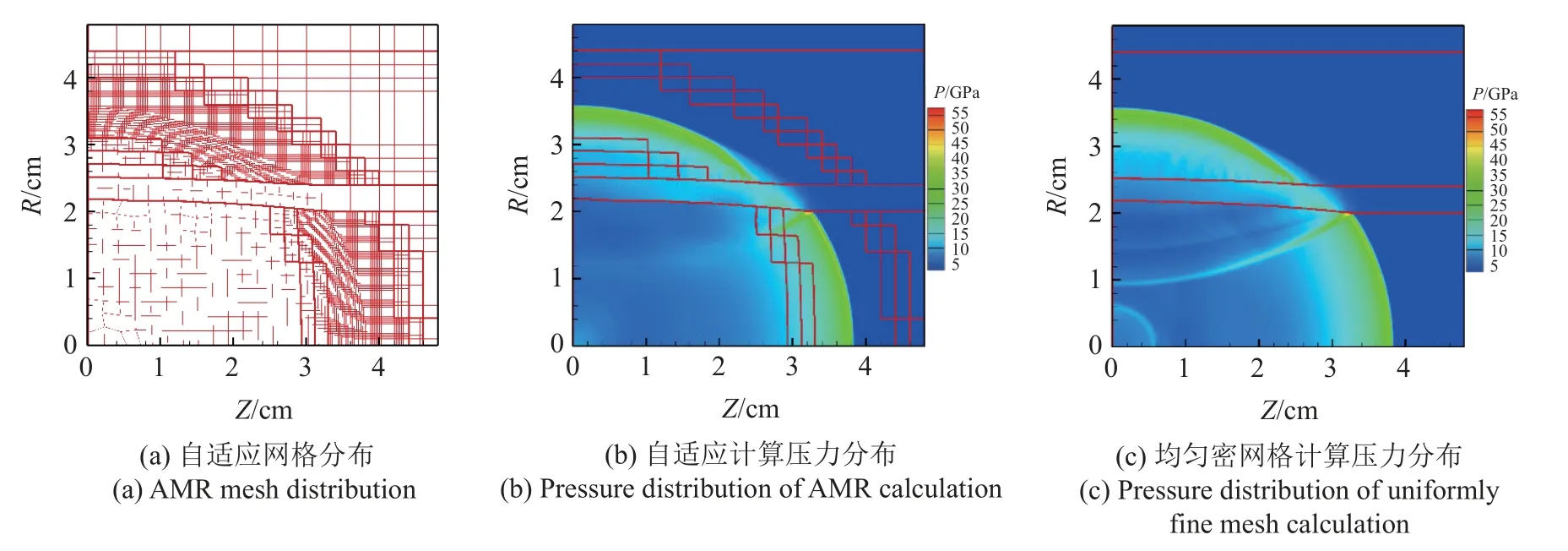
圖17 多分區炸藥爆轟隔爆問題模擬結果 (t=4 μs)Fig.17 Multi-block multi-material detonation problem (t=4 μs)

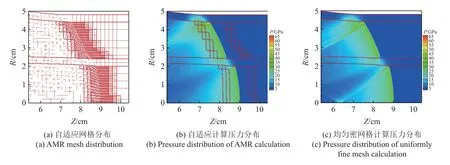
圖18 多分區炸藥爆轟隔爆問題模擬結果 (t=10 μs)Fig.18 Multi-block multi-material detonation problem (t=10 μs)

3.3 有限尺寸彎道爆轟問題

有限尺寸彎道中的爆轟問題廣泛存在于軍用裝備起爆系統的設計中,因炸藥截面尺寸較小,一般在毫米量級,若采用歐拉高精度方法,在彎道與炸藥之間的界面處會存在明顯的數值耗散,使得無法準確獲得爆轟虧損效應等定量結果.針對有限尺寸彎道爆轟問題,我們提出的基于爆轟彈塑性多介質流體力學程序的Lagrange 非結構網格多層自適應方法會比較適用.我們設計了如圖19 所示的算例,直管段長度為1 cm,彎道炸藥內半徑為1 cm,炸藥截面厚度為0.2 cm,彎道炸藥內、外各放置一層金屬鋼,厚度均為0.2 cm.爆轟波在直管端部起爆后,形成一維爆轟進入彎道溝槽中,因金屬材料邊界曲率的影響,凝聚炸藥爆轟與惰性金屬材料之間存在復雜的相互作用.初始時刻沿圓周方向炸藥區設置210 個網格,半徑方向設置10 個網格,內側鋼和外側鋼網格規模與炸藥區一致.初始徑向網格尺寸為0.2 mm,計算中設置自適應加密層數為3,因此最小網格尺寸為0.025 mm.在炸藥區,自適應加密判據為0.01<λ<0.99,其中 λ 為反應份額;在金屬材料鋼中,自適應加密判據為 ?p>3.5,p為網格單元的壓力.采用接觸滑移算法處理炸藥與金屬鋼之間的相互作用,在這個算例中,采用切向不做約束的單純滑移算法,實際計算中炸藥與鋼之間會存在摩擦,這方面的影響在日后的研究中會深入開展.

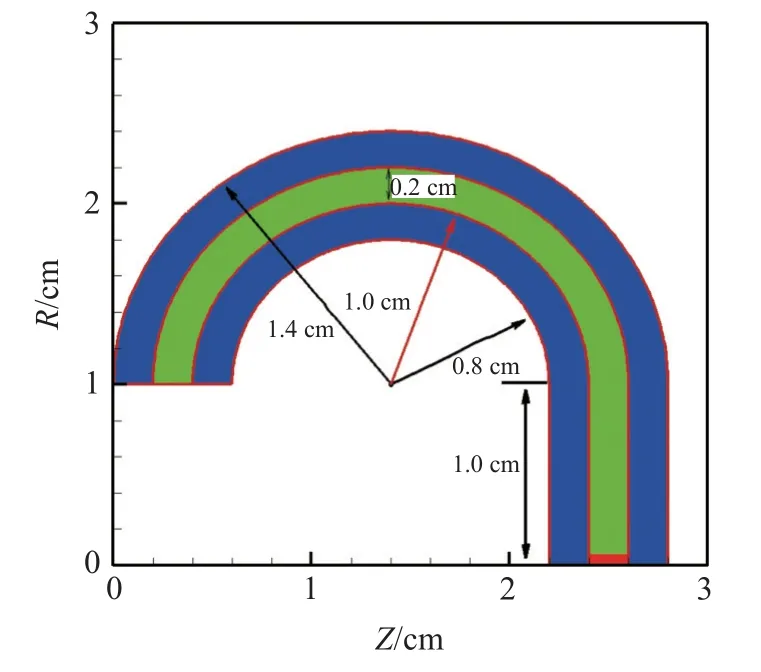
圖19 有限尺寸彎道爆轟問題初始幾何 (綠色:高能炸藥,藍色:金屬鋼,紅色:CJ 狀態爆轟產物)Fig.19 Initial geometry of detonation problem in finite-size curved pipeline (green:high-explosive,blue:steel,red:reactive product of CJ state)

圖20 給出了彎道爆轟不同時刻的流場分布.如圖20(a)所示,在直管中,形成穩態爆轟波自下而上傳播,流場和自適應加密網格沿直管中線左右對稱.需要注意的是,因側向約束的影響,爆轟波陣面在炸藥與金屬交界處略有彎曲,這個側向影響會使爆轟波傳播能量產生一定虧損.隨后,直管中爆轟波傳入彎道中,如圖20(b)～圖20(d)所示,靠近內界面的爆轟波被稀疏,靠近外界面的爆轟波被壓縮,出現了復雜的非理想爆轟現象.爆轟波在彎道中傳播的過程中,密網格始終跟隨爆轟波陣面和金屬鋼中激波自適應加密,波后膨脹區網格自適應稀疏.在這個復雜幾何構型中,Lagrange 自適應模擬即能清晰地保持物質界面,保障激波間斷處網格分辨率的同時,緩解均勻密網格計算該問題時波后流場因網格大變形、畸變導致的計算不健壯的問題.在這個問題中,自適應模擬最大網格規模約4 萬,同程度均勻密網格模擬網格規模為40.32 萬,可見自適應模擬節省了約90%的計算量.

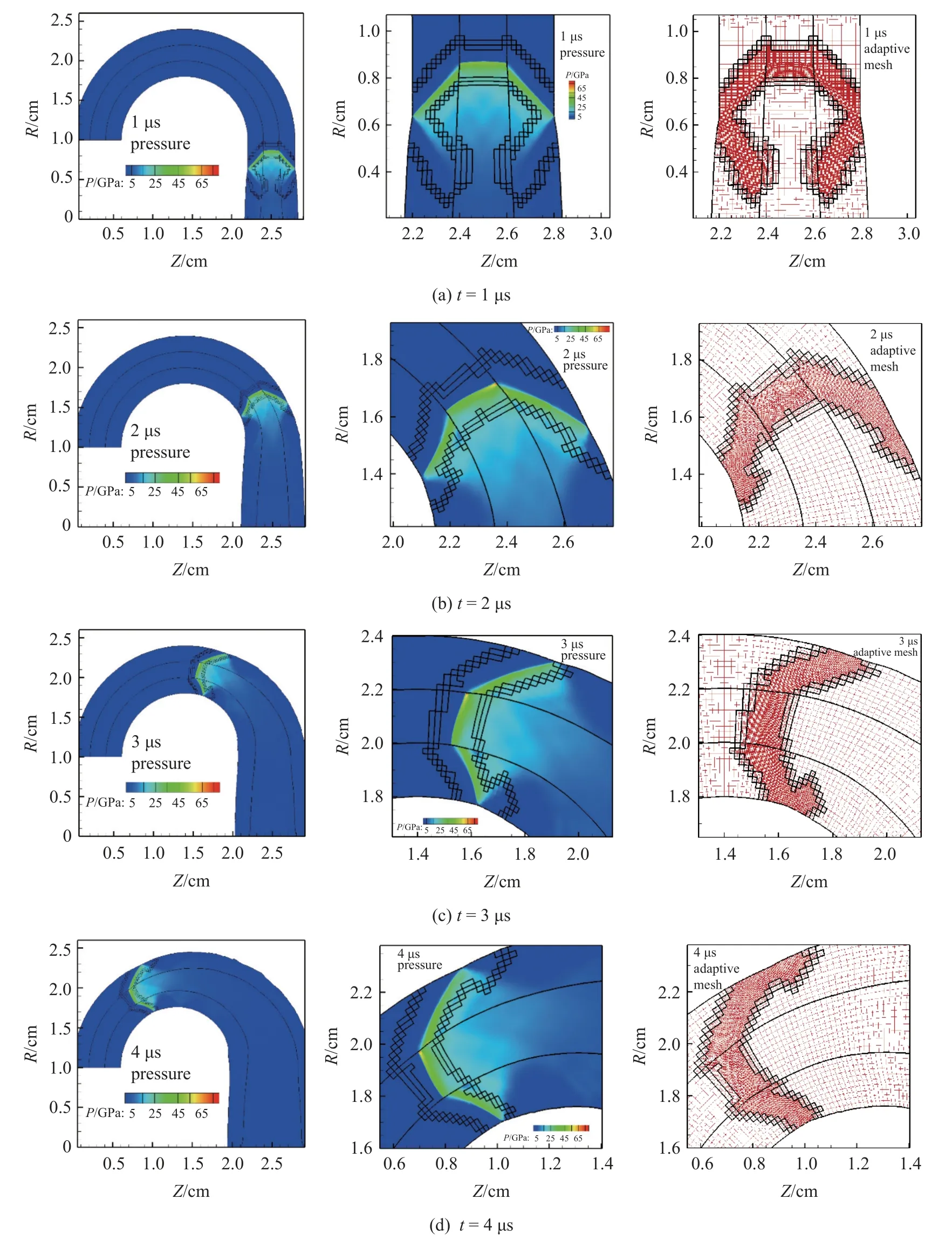
圖20 有限尺寸彎道爆轟傳播問題不同時刻壓力和網格分布 (左:整體流場壓力分布,中:局部放大壓力分布,右:局部放大網格分布)Fig.20 Simulation results for detonation problem in finite-size curved pipeline (left:pressure distribution,middle:local enlarged pressure distribution,right:local enlarged mesh distribution)

4 結論

本文針對爆轟驅動多介質問題的高分辨率健壯數值模擬需求,提出了適應于爆轟彈塑性多介質Lagrange 流體力學程序的非結構網格多層自適應加密與稀疏技術,在發揮非結構多層自適應數據結構靈活性優勢的基礎上,通過將有效網格壓至一層進行Lagrange 計算,避免了Lagrange 框架下多層網格分別計算帶來的層間耦合困難.更進一步地,實現了Lagrange 多層AMR 與接觸滑移算法的自適應耦合,使其對包含復雜幾何邊界的多分區、多介質問題有很好的適應性.采用上述AMR 方法,實現了拐角爆轟、多層炸藥隔爆、有限尺寸彎道爆轟等多個復雜多介質、多分區問題的Lagrange 多層AMR 模擬,獲得了豐富的凝聚炸藥爆轟與彈塑性介質相互作用的流場圖像.

后續工作將針對凝聚炸藥爆轟與惰性金屬材料相互作用規律開展深入系統的研究,包括本文涉及的復雜爆轟驅動多介質問題的計算條件和物理模型參數的定量標定,在此基礎上獲得不同炸藥、不同約束材料和不同幾何構型下爆轟約束效應及其非理想行為的規律性認識.