預測城市河流污染物濃度的對流擴散模型
孫景琛
(山西開放大學,山西 太原 030027)
1 河流概況
實驗河流里韋林河位于英格蘭東北部謝菲爾德市西北部。實驗地區位于是里韋林河的下游地區。平均降雨量為每年834.6 mm。實驗場地西南地勢高于東北部分,實驗地海拔最高為96.2 m(熒光劑投放點)和下游測點海拔最低為88.8 m。
2 實驗方法
2.1 投放熒光劑和測量背景濃度
在里韋林河道上游選擇有利于溶質在河流橫截面方向快速混合的地點作為投放點,為避免對河流水質造成污染,本實驗采用熒光劑示蹤劑作為污染物的替代品,熒光劑的優點是每一個分子有獨特的激發和發射波長,不需要進行生化反應實驗可現場獲取讀數。本實驗采用的熒光劑探測儀的靈敏度為0.02 ppb,由于儀器誤差,在熒光劑從投放點運動到各測點之前,或沒有投放熒光劑時,儀器仍會顯示一些或正或負的背景讀數,同時因為熒光劑經過較長距離的對流擴散等運動,在下游河水中的濃度較低,儀器讀數較低,不易與背景濃度分辨。因此在投放熒光劑之前,需要在投放點和下游各測點取樣,以便作為空白樣本,消除儀器誤差和背景濃度對實驗的影響。
2.2 測量下游熒光劑濃度
下游各測量點之間應有適當的間距,以利于了解河流中污染物濃度時間分布隨距離的變化。本實驗中從上游到下游依次排列為測量點10、測量點6、測量點7、測量點8,測量熒光劑的濃度與時間數據集,并在每個測量站點繪制濃度與時間圖,
本次實驗在同一投放點共投放三次熒光劑,實驗人員需要分別在投放點下游的4 個不同的測量點,在相同的時刻和時間間隔測量河水中的熒光劑濃度,然后繪制四個不同測量點的濃度隨時間變化,見圖1。
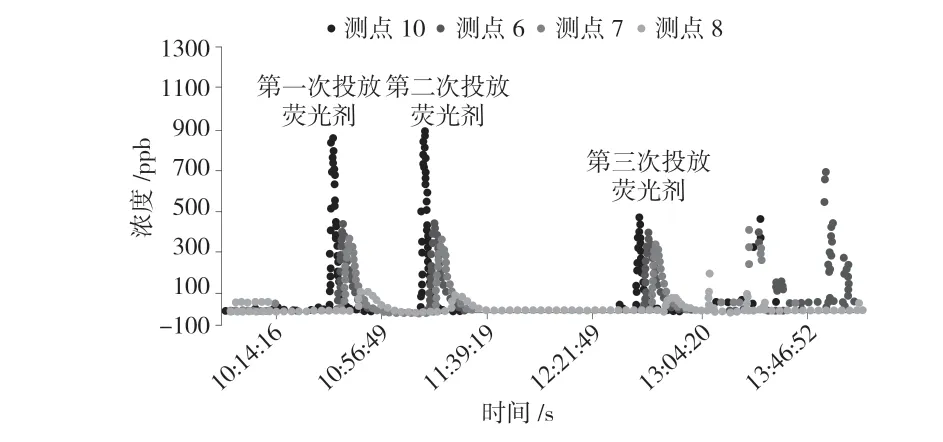
圖1 不同測量點熒光劑濃度隨時間變化圖
2.3 其他相關數據
實驗人員從河流左岸到右岸依次等距(0.5 m)測量從河底到河面的深度,目的是計算河道斷面總面積,需要測量投放點與各測量點之間的直線距離、曲線距離和高度差,以求得計算河床坡度,另外還需要各測點的水流平均流速。
3 建立對流擴散模型
3.1 數據處理
在實際現場實驗中,共投放三次熒光劑,然而第三次投放形成的測點10 濃度時間曲線的峰值比前兩次要低,這意味著它在重復實驗中與前兩次實驗表現不同,此外測點10 的位置接近投放點,因此舍棄測點10 的數據。出于實用性和篇幅的考慮,本文僅以測站6 和測站8 的數據為例,通過第一次熒光劑投放后的濃度時間分布來研究對流和擴散過程,見圖2。

圖2 第一次投放后測點 6 和測點 8 熒光劑濃度與時間關系圖
數據處理需要去除各測點的背景噪音。分別從測點6 和測點8 在熒光劑到達之前的平坦區域選擇5 分鐘時間段,并計算這段時間內的平均濃度,將其作為此測點的熒光劑背景讀數。從所有的濃度數據中減去背景讀數并將負讀數設置為0。圖3 顯示了去除背景讀數前后的0~10 ppb 濃度區間的放大圖。

圖3 背景讀數部分放大圖
在一次投放形成的熒光劑羽流全部離開一個測點后,下一次投放形成的熒光劑羽流會逐漸運動到該測點。因此需要識別該測點上一個羽流與下一個羽流的連接點,即讀數停止減少并開始增加的時刻,數據處理的方式是將所有低于臨界值(由峰值濃度的1%、3%和5%定義)的數據集剪裁,并且識別點之前和之后的濃度應設置為0。圖4 給出了以峰值濃度的5%為裁剪點處理后的測點6 和測點8 的濃度時間圖。
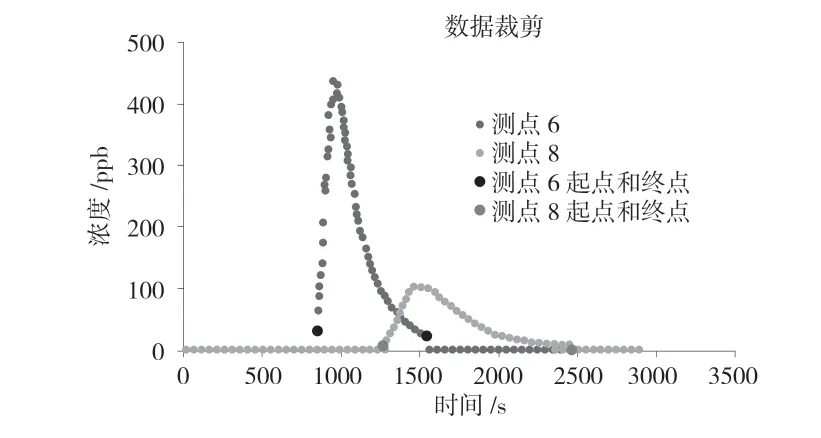
圖4 測點6 和測點8 的5%臨界點
3.2 建立對流擴散模型
在已知上游濃度隨時間變化的情況下,本對流擴散預測模型將有助于了解其運動到下游測點的濃度時間分布。通過計算分散系數,根據一對上下游測站的熒光劑濃度時間剖面,可以建立對流擴散模型。
河流中溶質的混合過程由對流、擴散、局部水流紊動組成。在忽略局部水流紊動的情況下,將前兩個物理過程用下面的對流擴散方程方程來表示。
式中:x、y、z 為坐標尺寸,x 為縱向,y 為橫向,Z 為垂向;u、v、w 為x、y、z 方向的速度分量;e 為擴散系數;c 為濃度。
由于僅研究基于河流流動方向的縱向混合,下游測點的熒光劑濃度的一維解被簡化為如下對流擴散方程:
式中:C(xds,t)為下游測量點xds時間t 時的濃度;C(xus,γ)為上游測量點xus某時刻的濃度;T 為微小時間段內的熒光劑從上游運動到下游測點的時間;Kx為縱向分散系數;t 為預估下游濃度的時刻與上游投放時刻之間的時間間隔;dγ為每個微小時間段的持續時間。
由上游熒光劑濃度Cxus推算下游熒光劑濃度Cxds需要利用微積分的思想,關于上游測點的濃度分布可以看作是很多次熒光劑投放,每一次投放一個微小時間段γ內的熒光劑總量,Cxus以測點6 和測點8 為一對上下游組合,測點6 的熒光劑經過一段行進時間后運動到測點8,測點6 的濃度分布可以拆分成多次的微小投放,每一次微小投放在下游測點8 都會形成相應的濃度Cxds。疊加同時刻各下游測點8的微小濃度值,構成下游熒光劑濃度實際分布,見圖5。
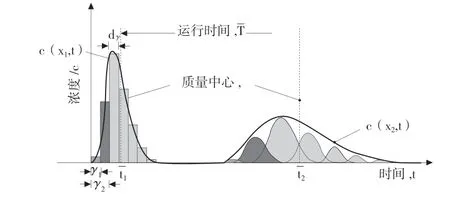
圖5 對流擴散模型疊加原理示意圖
3.3 檢驗質量平衡
上游及其相關下游測量點之間的溶質質量平衡是對流擴散模型的基礎。上下游測點的羽流內溶質質量是分別是其濃度與時間曲線下方的面積,可以通過計算下面的方程來解決。
然而,由于測量誤差和截面混合不完全,上下游的真實數據始終不能進行質量平衡。因此,通過將所有下游數據都乘以上游質量和下游質量之間的比率MB 來實現質量平衡。
通過計算得到測點6 和測點8 質量平衡結果。測點6:Mus=116313.6;測點8:Mds=52453.1;MB=2.2,見圖6。
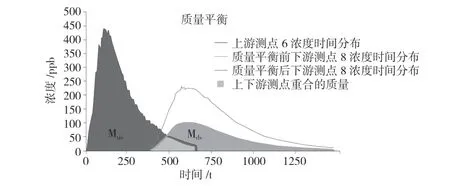
圖6 質量平衡
3.4 確定模型參數
通過求解下面的力矩方程,可以得到方程2 中的臨界系數Kx。
3.5 優化模型參數
本實驗共投放3 次染料,有4 個熒光劑濃度測量點,可以將未用于組建對流擴散模型的上游測點的數據輸入模型中,預測下游測點的濃度,判斷預測值是否與經質量平衡處理后的實際值吻合。之后通過計算參數Rt2來檢查對流擴散模型預測的優劣,使Rt2越接近1 的參數值最好。最后,對參數進行優化,使預測數據與真實數據最大程度地吻合,正式建立模型。
式中:mt為下游經質量平衡后的實際濃度;pt為下游預測濃度。
通過不斷改變Kx、裁剪點和不同的測量點組合,得到在Kx=0.75 時,Rt2等于0.93 接近于1,最終以Kx=0.75 建立用于預測上游污染物排放對下游河流影響的對流擴散模型。
3.6 水質模型耦合
對流擴散模型可以與其他模型相結合,例如借助SOBEK模型與下水道模型結合[1],獲得排污口溢漏特征,可以應用在河流中設置合流式排污口,排放經處理后達到排放標準的城市污水,預測下游不同距離的污染物濃度,以減輕城市污水處理的壓力。又如與河道水文模型結合,有助于獲得準確的河流流量,分析污染物擴散到下游的預測濃度剖面和危害程度,可用于航運過程中的船舶污染物泄露后的情況,及時做好應對措施。
3.7 預測不確定性
就對流擴散模型本身的準確性而言,還存在很多不確定性。一是混合過程還取決于局部水流紊動,而局部水流紊動隨時間和位置的不同而變化很大。更具體地說,局部水流紊動在不同時間的表現并不相同,并且涉及很多物理量,包括粗糙度、泥沙輸送速率等。然而,它們在每個河流斷面都是可變的和多樣的。
此外,對流擴散模型中有很多假設,例如質量平衡甚至流量等。但河床上存在渦流和污染轉化,因此上下游質量不平衡。此外,流量假定為速度乘以橫截面積。然而兩者都是近似值,并且隨時間和空間的變化而變化。
4 結語
對流擴散模型可以定量預測城市河流中污染物的輸移和擴散過程,為保護生態環境和保證水資源安全提供支持,希望此模型可以在類似河流水質預測中起到一定借鑒作用。

