氣體波動引起的彎曲流道氣波機振蕩管結構動態響應研究*

尹 彬,張博旭,王澤武

(大連理工大學 化工機械與安全系,遼寧 大連 116024)

0 引 言

氣波制冷機是利用氣體的壓力能產生激波和膨脹波進行制冷的一種特殊設備,在石油化工[1]、航空航天[2]及食品速凍保鮮[3]等領域得到了廣泛應用。

近年來,胡大鵬等人[4-7]創新性地提出了外循環耗散式雙開口氣波機,解決了傳統氣波機熱能難以回收和積液的問題,使制冷綜合效率得到顯著提升。代玉強等人[8-13]研究了直流道氣波機結構和操作參數對雙開口氣波機制冷性能的影響;然而直流道氣波機同時也存在較大的非等熵流動損失。為此,趙一鳴等人[14]進一步提出了彎曲流道雙開口氣波機,該氣波機既有利于減小高壓射氣損失,又可降低中壓端口內的氣體流動損失,降低熱端能量耗散,因此可顯著改善氣波機的工作性能。在彎曲角度設計參考工況下,各性能參數相對直流道的提升比例可達到25.3%。

波轉子是氣波機的核心工作部件,其振蕩管間插片厚度通常小于2 mm,且越薄越有利于提升氣波制冷機的制冷效率;但是插片也是氣波機中最為薄弱的元件,容易損壞而引發事故。吳響響等人[15-16]對直流道氣波機振蕩管內流場和波轉子模態進行了研究,得到了振蕩管內非定常流體激振力下插片元件的結構動態響應;但是,目前鮮有針對彎曲流道氣波機插片元件在流體流動誘導下動態響應的研究。

此外,為了研究流致振動問題,多場耦合技術在流體機械、輸流管道和航空航天等領域得到了廣泛應用[17-26]。

為研究彎曲流道氣波機在非定常高頻高壓流體激勵載荷作用下能否安全運行,筆者提出采用多物理場耦合方法,開發彎曲流道雙開口氣波機三維流固耦合數值計算模型,研究振蕩管內的非定常流場流動特性,進而提取復雜波動引起的流激力;然后,進行振蕩管插片元件結構動態響應分析和波轉子固有頻率分析;最終,判斷結構改進是否會引起氣波機不安全運行行為。

1 彎曲流道氣波機三維流固耦合模型

1.1 模型簡化

氣波機波轉子三維模型如圖1所示。

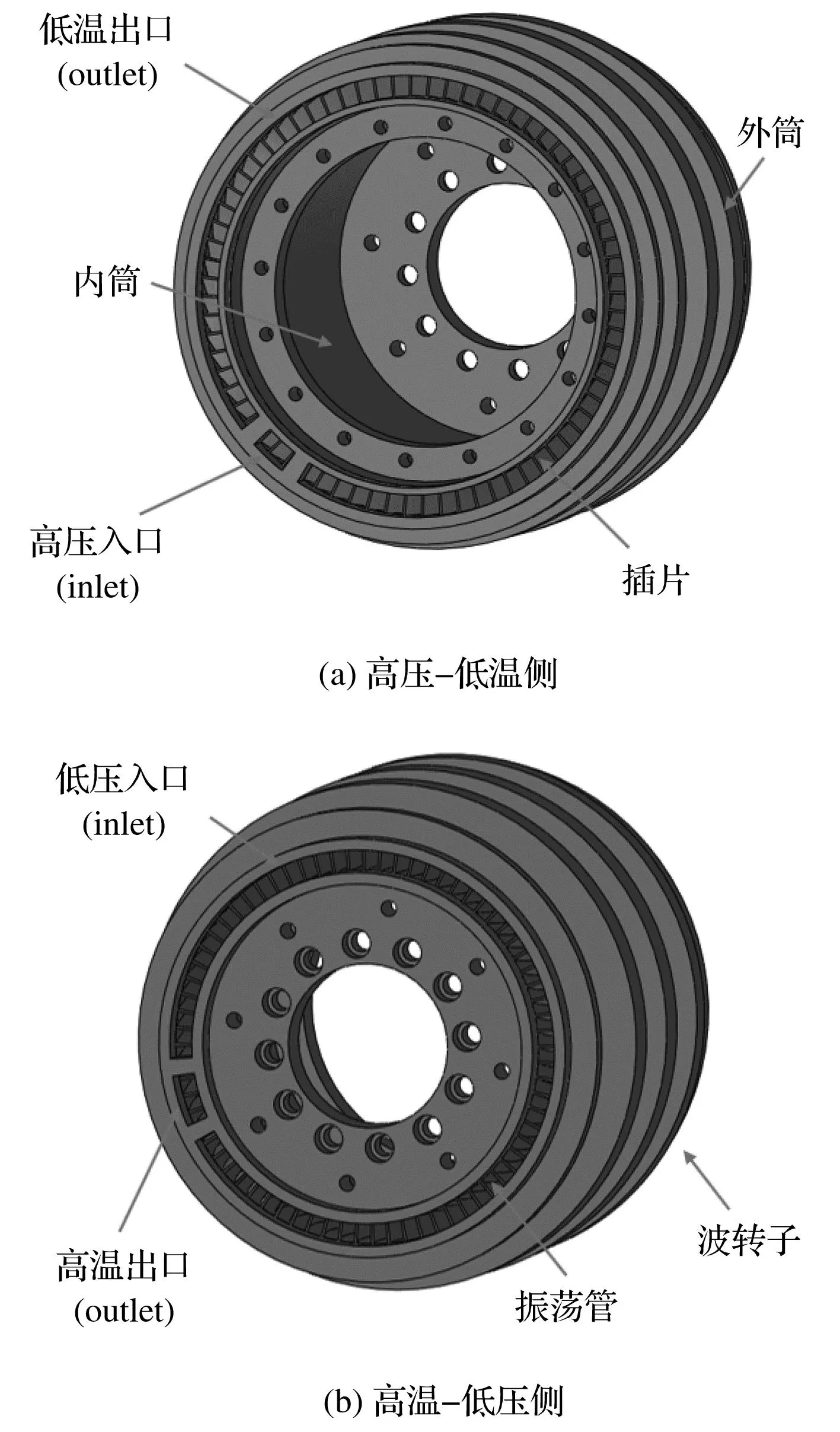
圖1 氣波機波轉子三維模型Fig.1 Three-dimensional model of wave rotor in the gas-wave refrigerator

圖1為雙開口氣波機波轉子,波轉子主要由內外筒、插片及密封元件組成。內、外筒體與插片組成橫截面近似長方形孔的72根振蕩管,圓周方向兩根相鄰振蕩管共用一根插片。

氣波機通過各進出氣口、波轉子與旋轉軸相連,并置于機殼內。為防止動、靜部件摩擦,其進出氣口與波轉子兩端設有微小間隙,一般要求間隙低于0.2 mm。

為確保波轉子變形在可控范圍之內,設計前需要精確計算波轉子在轉動過程中的變形量。

其他雙開口氣波機相關參數如表1所示。

表1 雙開口氣波機結構參數

振蕩管內氣體流動狀態復雜,網格數量、流固耦合數據交換、剛度矩陣求解等均會消耗大量計算資源,因此進行合理的模型簡化十分必要。

考慮到波轉子的振蕩管呈周期性分布,筆者從72根振蕩管取出7根振蕩管進行分析,中間5根管參與流固耦合主計算,外側兩根振蕩管作為支撐以防止內、外圓筒發生過大變形。

簡化后的模型不僅能夠準確模擬固壁反射、相鄰振蕩管端部之間的相互影響,而且還大大降低了計算規模。

流體域模型和對應結構域模型如圖2所示。

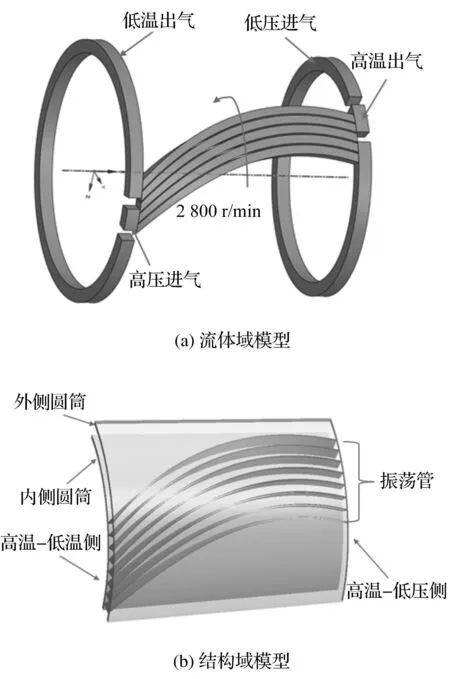
圖2 氣波機波轉子三維簡化模型Fig.2 Simplified three-dimensional model of wave rotor in the gas-wave refrigerator

1.2 三維數值模型開發與可靠性驗證

氣波機三維流體模型邊界條件有以下5種:

“壓力進口”邊界條件包括高壓進氣口和低壓進氣口;“壓力出口”邊界條件包括高溫出氣口和低溫出氣口;兩對“滑移邊界”邊界條件包括振蕩管內流體左端和高壓入口、低溫出口右端的接觸面、振蕩管內流體右端和高溫出口、低壓入口左端的接觸面;振蕩管內部流體默認為“內部”,流固耦合面均設置為壁面。

該彎曲流道氣波機工況壓比(PHP/PHT)為4。

4個進出氣口的壓力、溫度和水力直徑數據如表2所示。

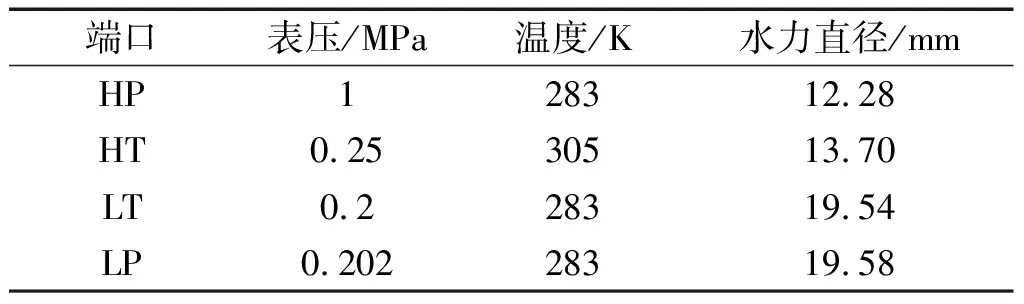
表2 雙開口氣波機進、出氣端口邊界條件

工程應用領域中,對湍流流動的模擬主要以RANS方法為主。在Fluent的相關設置中,筆者選擇k-ωSST模型作為湍流模型,把振蕩管和各進出氣口內氣體視為理想氣體,網格交界面按滑移邊界將各端面匹配,計算前根據表2為各進出氣口內流體設置初值。

在Transient Structural模塊中,筆者為固體域模型賦予不銹鋼金屬材料,流場穩定后,多周期流固耦合結果僅為單周期流固耦合的近似重復。

由于流固耦合計算對計算資源需求極高,因此,筆者根據流體域結果匹配數據量和時間步長,進行一個旋轉周期的流固耦合計算。

由于氣波機波轉子剛度大,其結構變形對流體流動影響甚微。因此,為提高計算效率,筆者選用單向流固耦合方法。流體域采用多區域網格劃分方法,以六面體結構化網格為主。

為準確計算插片附近流場分布與激勵載荷波動,筆者在進出氣口和振蕩管流體域壁面設置了一定的初始厚度和增長率的膨脹層。

接下來需要進行網格無關性和時間獨立性驗證。筆者設置網格尺寸分別為0.5 mm、0.75 mm、1 mm、1.5 mm和2 mm,時間步長分別為1×10-6s、5×10-6s、1×10-5s、2×10-5s和5×10-5s;以網格尺寸和時間步長分別作為自變量,中間振蕩管所受力矩作為變量,將力矩值在不同網格數和不同時間步長下進行連線,得到可靠性驗證結果,如圖3所示。

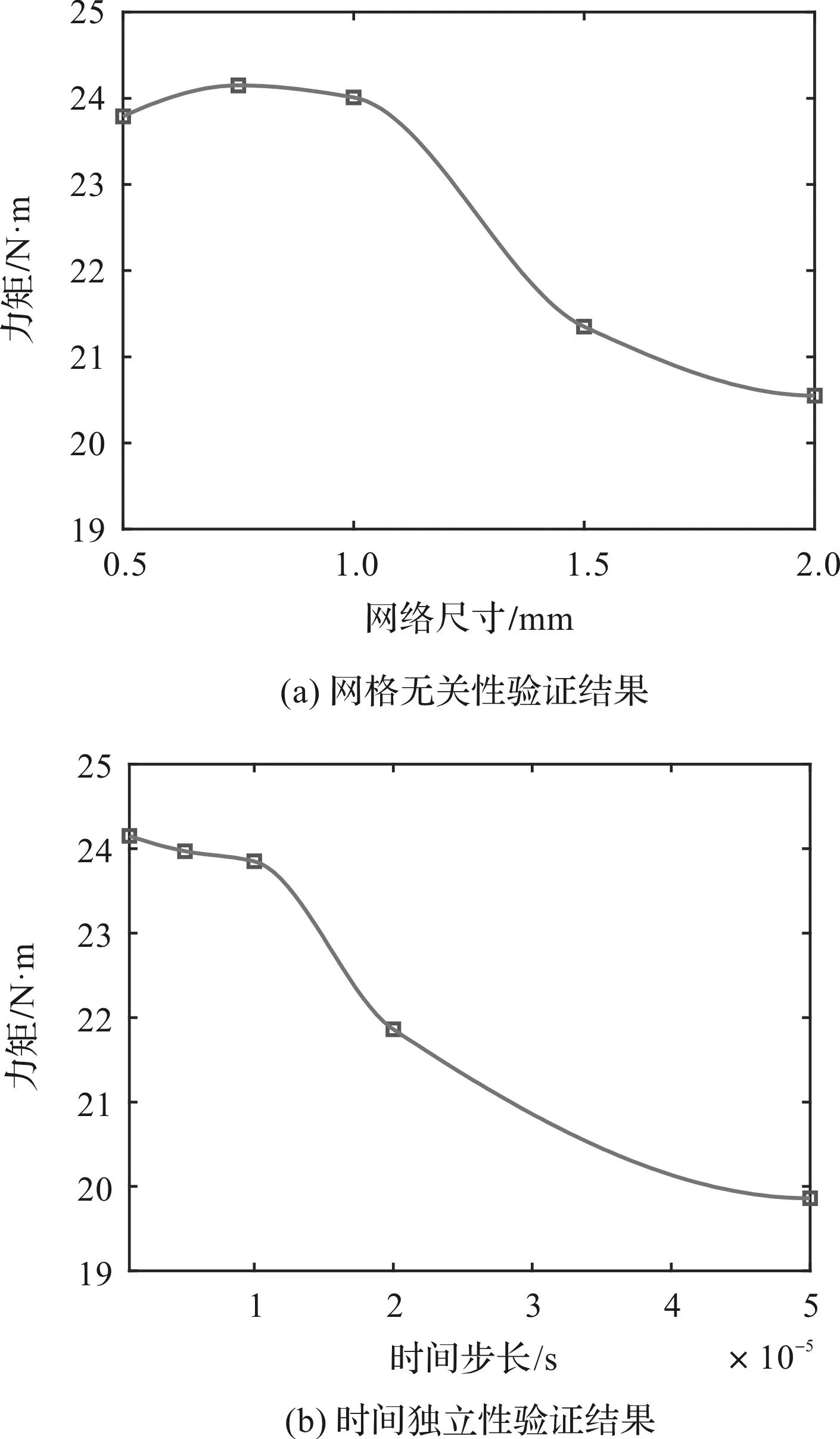
圖3 可靠性驗證Fig.3 Reliability verification

當網格尺寸小于等于1 mm,時間步長小于等于1×10-5s時,中間振蕩管所受的力矩變化不大,說明1 mm的網格尺寸已達到網格無關,時間步長取1×10-5s可保證計算速度和精度。

氣波機波轉子的轉速為2 800 r/min。為更好地捕捉管內激波、壓縮波和膨脹波,筆者設置總時間步為15 000步,波轉子共旋轉約7圈。

為保證流固耦合計算的準確性,筆者設置波轉子插片網格尺寸與流體域一致,內外筒網格尺寸為2 mm,最終得到波轉子數值計算網格模型,如圖4所示。

2 彎曲流道振蕩管流場特性分析

2.1 壓力場分布

彎曲流道氣波機振蕩管插片結構動態響應主要由振蕩管內流體壓力場波動引起。

為了研究振蕩管內壓力場隨波轉子旋轉的波動特性,筆者繪制出5根振蕩管高壓進氣和低溫排氣階段的壓力分布云圖,如圖5所示。

由圖5(a)可知:在高壓進氣階段,振蕩管與高壓入口接通,高壓氣體入射振蕩管并產生激波,隨著時間推移激波逐漸向右側高溫出口傳播,經過之處壓力升高,振蕩管內壓力波動劇烈。

從圖5(b)可知:低溫排氣階段振蕩管與低溫出口接通,管內壓力場較為平穩。振蕩管端口與固壁接觸時產生膨脹波,膨脹波使管內壓力降低。彎曲流道氣波機波轉子壓力在0.069 4 MPa～1.141 0 MPa的范圍內波動,波轉子旋轉,振蕩管兩側端口隨著歷經與各出入口接通和斷開的過程。

振蕩管與高壓入口接通時,管內壓力較大且波動劇烈;與低壓入口接通時,管內壓力較小且分布均勻;當振蕩管左端口與高壓入口完全接通時,靠近高壓入口端管內的局部壓力比高壓入口的入射壓力1 MPa高出14.1%,并且該位置兩側壓力梯度很大。

振蕩管與高壓入口和高溫出口的漸開漸閉過程所引起的氣體波動行為較為復雜,振蕩管內壓力隨著波轉子轉動而呈周期性分布,壓力較大值主要集中在靠近高壓的入口側。

2.2 激勵載荷的提取與分析

振蕩管內高頻波動的非定常壓力場是引起振蕩管插片振動的主要激勵源。因此,對波轉子振蕩管插片所受激勵載荷進行分析是掌握氣波機振蕩管振動特性的基礎。

由圖5(a)可知:振蕩管與高壓入口接通處的壓力較為集中,管內壓力存在強間斷。因此,筆者選取具有代表性的中間振蕩管迎風側第1、第7節點,以提取壓力載荷。

迎風側第1、第7節點位置與壓力-時間曲線如圖6所示。

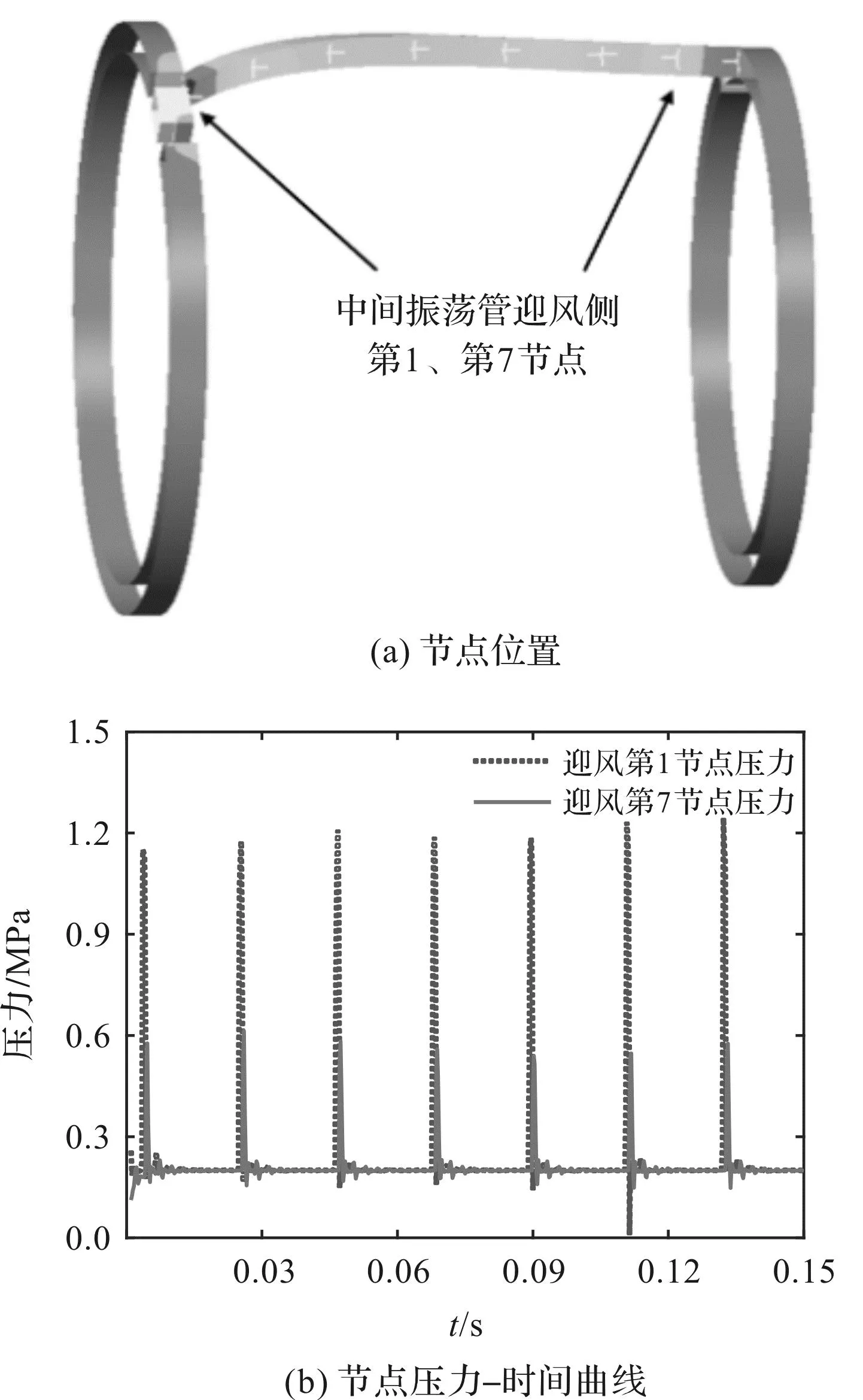
圖6 迎風側第1、第7節點位置與壓力-時間曲線Fig.6 Position and pressure-time curves of the first and seventh nodes on the windward side

由圖6(b)可知:第1周期數據在波峰前有波動,與后續數據呈現的規律存在較大差異,因此,需要舍棄第1周期數據。

迎風側第1、第7兩個節點壓力峰值分別為1.179 MPa和0.559 5 MPa,第7節點壓力峰值時間較第1節點延后0.006 s;兩點壓力均呈現快速的先上升后震蕩衰減的趨勢,到下一個周期重復該規律,第1節點壓力衰減速度快于第7節點。

第5周期第1節點迎風側和背風側壓力與壓差曲線,如圖7所示。

由圖7(a)可知:迎風側第1節點壓力從最大值到最小值僅用時0.000 4 s,背風側壓力波動較小;迎風側比背風側早0.000 2 s到達最大值,早0.000 4 s到達最小值。

由圖7(b)可知:在振蕩管同一位置處,迎風側與背風側壓力存在一定的差值,大約在-0.185 6 MPa～0.971 2 MPa之間,振蕩管插片同時受左右兩側壓力作用;正向壓力主要受迎風側作用,背向壓力受二者共同作用(這樣復雜的壓力波動會引起振蕩管不期望的振動,從而降低氣波機振蕩管的疲勞壽命,尤其是在插片更薄時)。

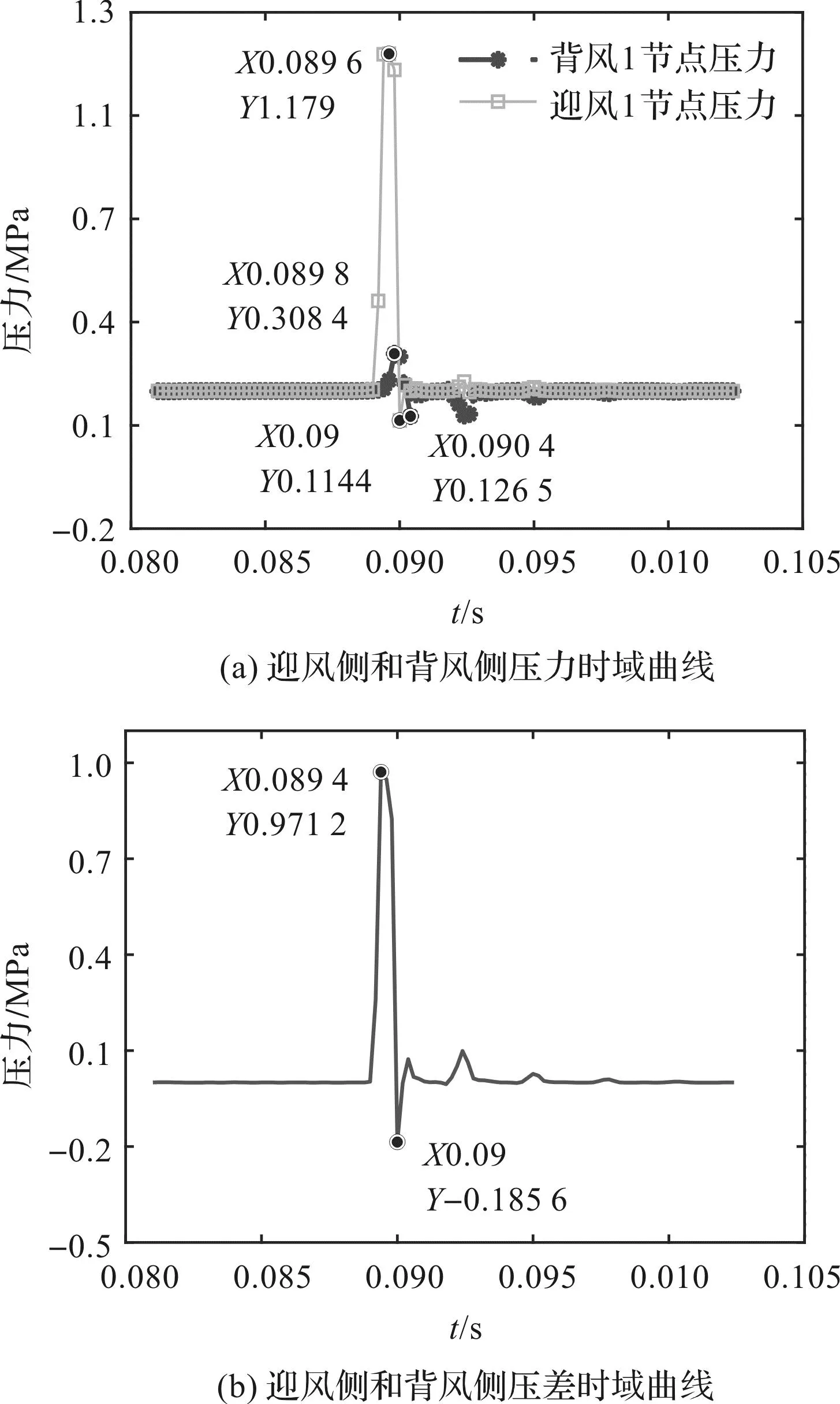
圖7 第5周期第1節點迎風側和背風側壓力與壓差曲線Fig.7 Pressure and pressure difference curves of the windward side and leeward side of the first node incycle 5

3 振蕩管結構動態響應及模態分析

3.1 位移場分析

筆者選取流場計算第5周期的壓力載荷數據,利用Workbench流固耦合平臺,導入Transient Structural模塊,進行振蕩管結構強度的瞬態計算。

為了直觀表示彎曲流道振蕩管的位移場分布,以及不同時刻、不同位置的位移動態變化規律,筆者繪制了中間振蕩管迎風側插片位移云圖和中間振蕩管迎風側插片中線的位移-時間-位置三維曲線,如圖8所示。

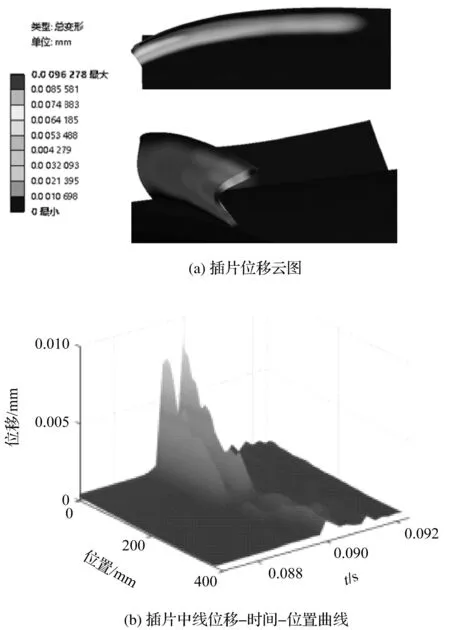
圖8 彎曲流道振蕩管迎風側插片位移場Fig.8 Displacement field of the windward side insert of the oscillating tube with curved channel

為了便于研究振蕩管插片最大位移節點的位移變化規律,筆者繪制迎風側第1節點位移-時間曲線,如圖9所示。

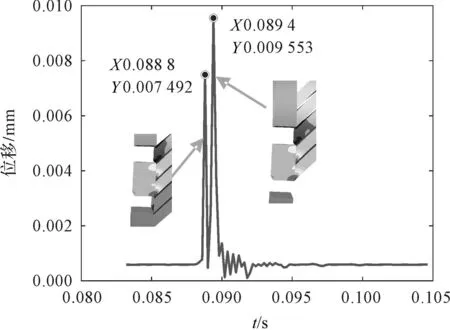
圖9 迎風側插片第1節點位移-時間曲線Fig.9 Displacement-time curve of the first node of the windward side insert

由圖8(a)可知:彎曲流道振蕩管最大位移發生在高壓入口處的插片中間位置,最大位移為0.009 6 mm。

圖8(b)中的兩個峰值表明,振蕩管位移幅值同時受左右兩側壓力的影響,在整個周期內靠近高溫出口處均未發生明顯變形。

由圖9可知:中間振蕩管迎風側插片的最大位移發生在0.089 4 s時刻,此時振蕩管剛好與高壓入口完全分離,而后一根振蕩管與高壓入口尚未分離;次大位移發生在0.088 8 s時刻,中間振蕩管剛與高壓入口完全接通,后一個振蕩管尚未與高壓入口接通。當振蕩管與低壓入口接通時,插片位位移僅有小幅波動。

在非定常流體激勵載荷作用下,彎曲流道氣波機振蕩管插片會產生軸向位移,可能導致波轉子與進出氣口發生動靜部件摩擦。為此,筆者調取了振蕩管插片軸向位移最大時刻的位移云圖,如圖10所示。

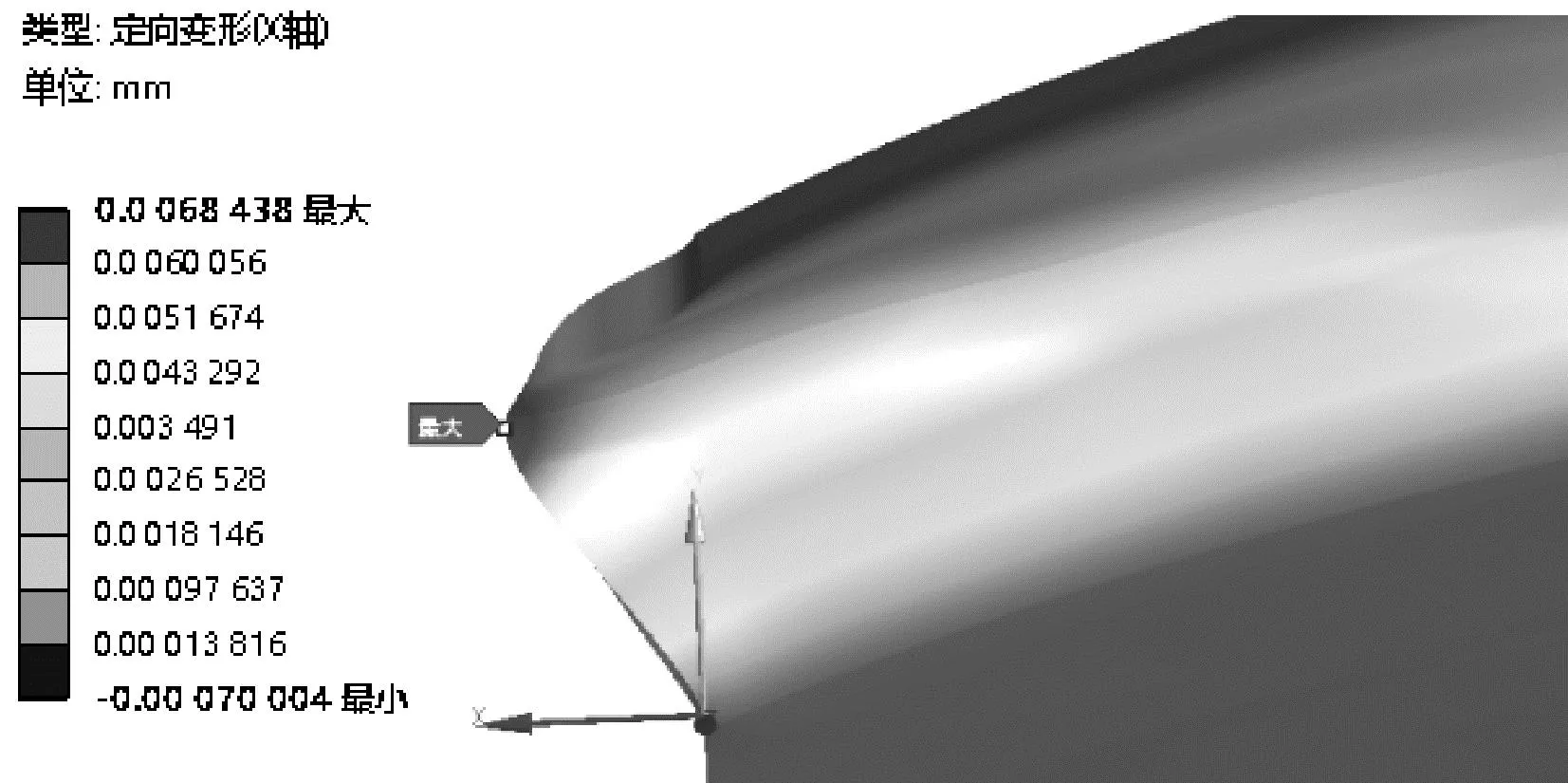
圖10 振蕩管插片最大軸向位移云圖Fig.10 Cloud image of the maximum axial displacement of the oscillating tube insert

由圖10可知:振蕩管插片最大軸向位移為0.006 8 mm,小于設計要求的0.2 mm,由此可以判斷,波轉子與進出氣口不會發生動靜部件摩擦。

3.2 應力場分析

為判斷振蕩管插片是否會發生強度失效,以及直觀表示振蕩管不同時刻、不同位置的應力動態分布,筆者繪制彎曲流道中間振蕩管迎風側插片應力場云圖和插片中線應力-時間-位置曲線如圖11所示。

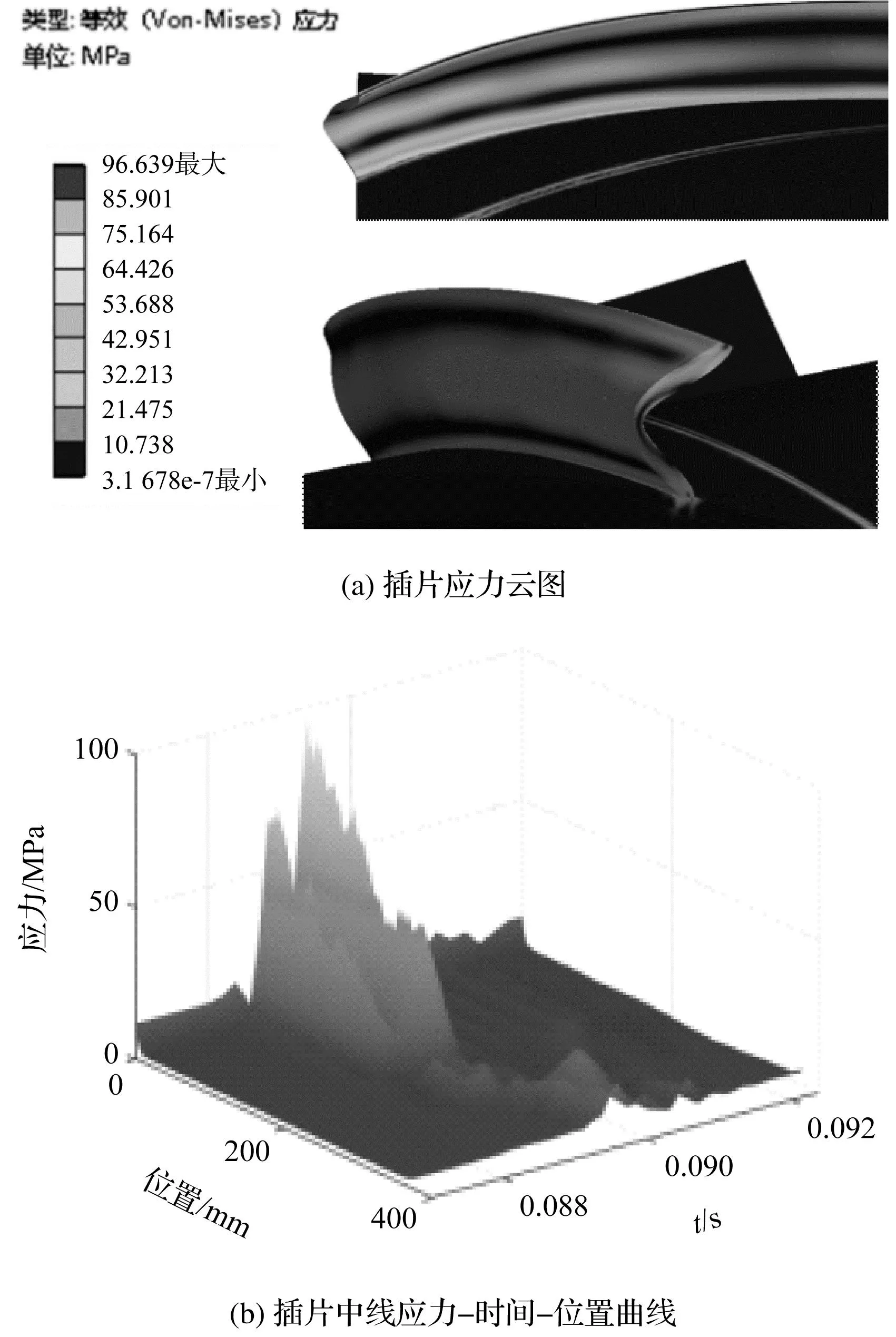
圖11 彎曲流道振蕩管迎風側插片應力場Fig.11 Stress field of windward side insert of oscillating tube with curved channel

筆者繪制插片第1節點應力時域曲線如圖12所示。

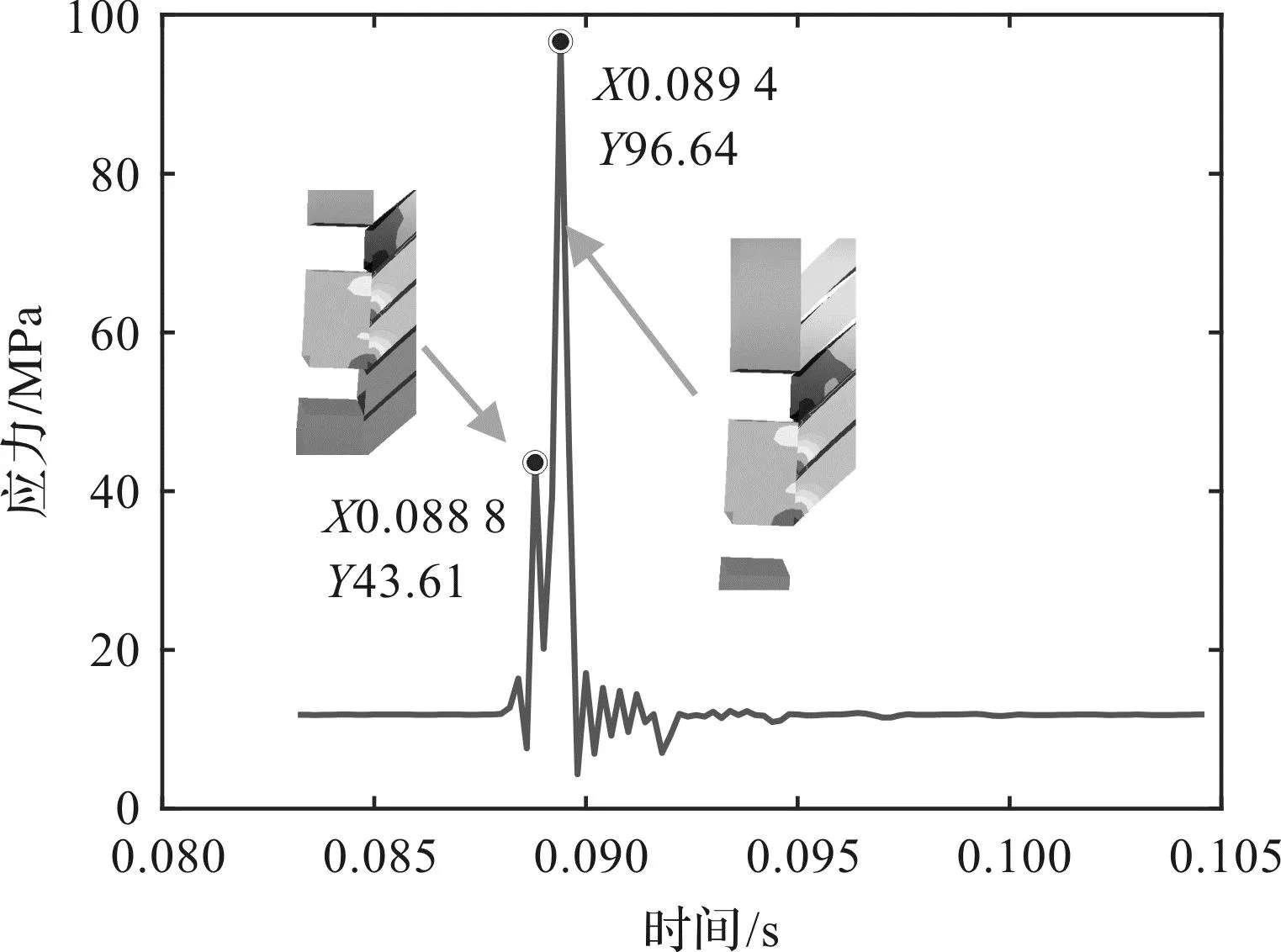
圖12 迎風側插片第1節點應力-時間曲線Fig.12 Stress-time curve of the first node of the windward side insert

由圖8～圖12可知:位移最大時刻與應力最大時刻相同;振蕩管插片應力最大處為插片與內外筒連接處,最大應力值為97 MPa,低于不銹鋼材料許用強度137 MPa;最大應力和次大應力發生時刻與大位移發生時刻規律相同。

3.3 模態分析

彎曲流道振蕩管迎風側插片位移和應力動態響應分析結果表明:在非定常流體激勵載荷作用下,振蕩管插片位移和應力值均在安全范圍內。

為了判斷氣體波動能否引起振蕩管振動問題,筆者對第1節點壓力載荷和振蕩管插片對應位置的位移分別進行傅里葉變換,得到彎曲流道壓力和位移幅頻特性曲線,如圖13所示。

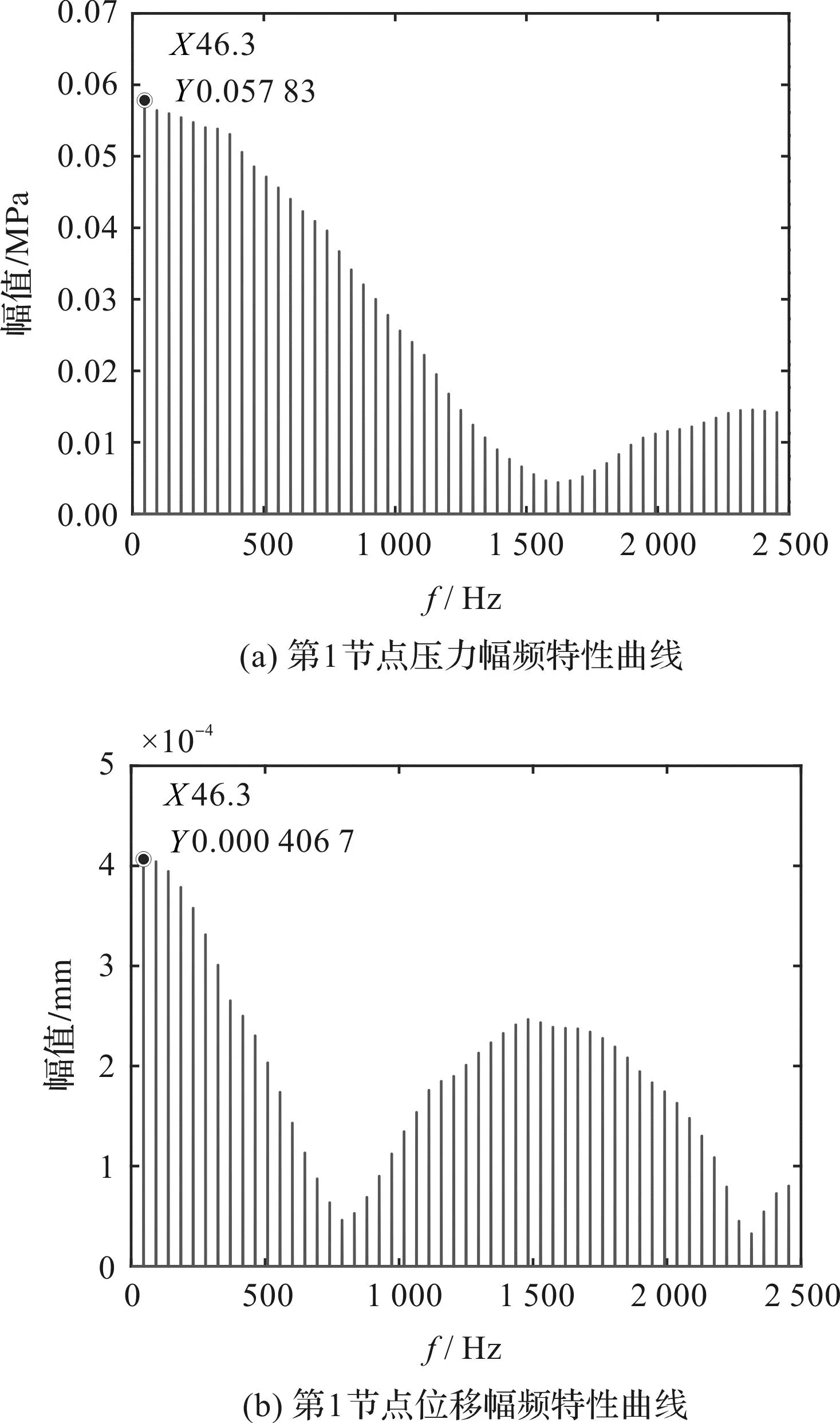
圖13 彎曲流道壓力和位移幅頻特性曲線Fig.13 Pressure and displacement amplitude-frequency characteristic curves of curved channel

由圖13可知:彎曲流道振蕩管迎風側第1節點壓力最大節點的流體激勵載荷和振蕩管插片位移頻率均為46.3 Hz,與該工況下氣波機轉動頻率46.7 Hz基本一致,這表明振蕩管插片的受迫振動是由氣波機電機旋轉引起的。

相同工況下,直流道氣波機振蕩管振動幅值最大節點為第7節點,其直流道位移時程和幅頻特性曲線,如圖14所示。

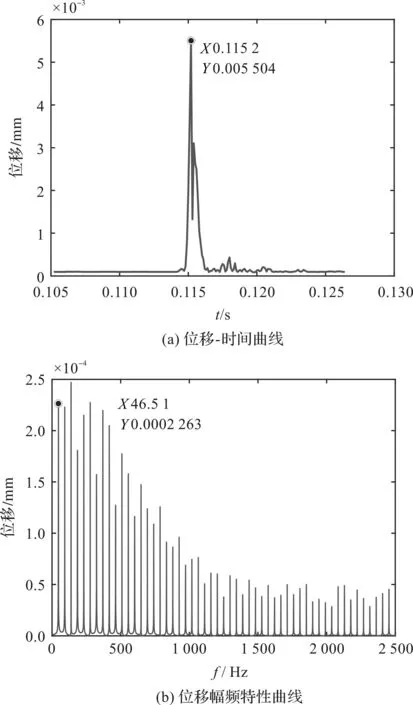
圖14 直流道位移時程和幅頻特性曲線Fig.14 Displacement time-history and amplitude-frequency characteristic curvesof straight channel

對比彎曲流道和直流道氣波機[15]位移動態響應可知:在相同工況下,彎曲流道位移峰值是直流道的1.74倍,但是二者振動頻率基本相同,均與轉速頻率46.7 Hz一致。

為了進一步明確氣波機是否會發生共振,筆者對波轉子進行模態分析,得到了波轉子的前4階模態,如表3所示。

表3 波轉子前4階模態

表3中,波轉子的第1階模態為87.76 Hz,與流體激勵頻率和電機旋轉頻率均不在共振區間內,因此可以判斷氣波機不會發生共振。

4 結束語

為研究彎曲流道氣波機在非定常高頻高壓流體激勵載荷作用下能否安全運行,筆者開發了彎曲流道氣波機波轉子三維流固耦合數值計算模型,并對氣波機振蕩管管內流場、結構動態響應及振動特性進行了研究。

研究結論如下:

1)彎曲流道振蕩管內壓力波動在0.069 4 MPa～1.141 0 MPa范圍內,并且存在明顯的壓力間斷,壓力最大值集中在振蕩管高壓氣體入口處,峰值高于入口壓力的14.1%。在一個旋轉周期內,振蕩管同一點的迎風側與背風側壓差在-0.185 6 MPa～0.971 2 MPa之間;

2)彎曲流道氣波機振蕩管內位移振幅最大值為0.009 6 mm,是直流道的1.74倍。雖然彎曲流道振蕩管氣波機插片位移振幅高于直流道振蕩管氣波機,但是其幅值僅在10-2mm以下,滿足0.2 mm的工程設計要求,因此可以判斷波轉子不會與進出氣口發生動靜部件摩擦;

3)彎曲流道和直流道氣波機振蕩管內流激力及受迫振動頻率均在46 Hz～47 Hz之間,與氣波機電機轉速頻率相當,但遠離氣波機波轉子固有頻率,因此可以判斷其不會發生共振。

筆者后續將重點關注振蕩管進氣角度、排氣角度和插片厚度等對波轉子動態響應特性的影響,以便為波轉子的結構優化提供參考。