基于等效風速的雙饋風力發電機動偏心故障特性分析

繩曉玲，鄧祖賢，萬書亭，韓旭超，豆龍江，張 雄

(華北電力大學 電力機械裝備健康維護與失效預防河北省重點實驗室，河北 保定 071003）

0 引言

根據全球風能理事會(GWEC）發布的《2022年全球風能報告》[1]，2021年全球風電裝機容量新增近94 GW。

風電行業蓬勃發展，大容量機型不斷推陳出新，風力機大型化趨勢愈發明顯。葉片加長，塔筒加高，系統柔性也隨之提升，這將使葉輪掃掠面內各點的風速差異與變化更為明顯。這種差異主要是由風剪切、塔影效應以及湍流等因素導致，并且會隨著時間和空間不斷變化，簡稱為風速時空分布差異。

風速分布的差異性會進一步影響風電機組氣動載荷，使得風電機組動態轉矩、轉速和偏航力矩等產生波動，也會導致機組功率損耗[2]和電力系統波動[3]。

本文選擇雙饋風力發電機的氣隙偏心故障作為研究對象，對等效風速下的偏心故障特征進行分析。發電機正常運行時，定、轉子間的氣隙是均勻分布的。氣隙偏心是發電機定子與轉子間氣隙空間分布不均勻的一種現象，約有90%的機械故障會導致氣隙偏心。學者通過理論分析計算氣隙磁場的變化，分析磁場特性，建立瞬態電磁場與多回路耦合的數學模型[4]，[5]來尋找偏心故障的電氣特性。文獻[6]通過建立時序電路模型來計算偏心量，并利用MATLAB/Simplorer進行電路聯合仿真驗證。文獻[7]，[8]總結了雙饋風力發電機氣隙偏心的研究現狀，給出了偏心故障特征頻率的一般表達式。

針對風力發電機偏心故障的研究大多基于葉輪輪轂中心處的平均風速，由于未考慮風剪切、塔影效應等實際風速影響因素，分析的方法或者結果可能與實際有所偏離[9]。因此，本文首先研究了考慮風速時空分布的等效風速模型，然后基于等效風速模型研究雙饋風力發電機氣隙偏心故障特征的變化，并通過仿真與平均風速下的故障特征進行對比分析，最后用實驗進行驗證。

1 等效風速模型

本文針對葉輪掃掠面內的風速分布問題提出了普適的n-葉片等效風速模型來表示風速分布的時空差異，根據相關研究[2]，[9]，葉輪掃掠面內的等效風速VE可表示為輪轂平均風速VH、風剪切影響風速分量VQ和塔影影響風速分量VT之和。

式中：R為葉輪半徑；H為輪轂高度；α為風剪切指 數；βb為 槳 葉 的 方 位 角；下 標b=1，2，3，分 別 代表3個葉片；D為塔筒半徑；l為葉輪旋轉平面到塔中心線的距離；ωY為葉輪轉動角頻率；r為分析點到風輪轉軸的徑向距離；M為輪轂風速與空間平均風速的轉換差率。

對 式(2）和 式(3）化 簡 得：

將 式(6），(7）帶 入 式(1）并 化 簡，得 到 等 效 風速的完整表達式。

根據式(8），繪制不同型號風力發電機在輪轂風速VH=11 m/s時的等效風速波動曲線(圖1）。

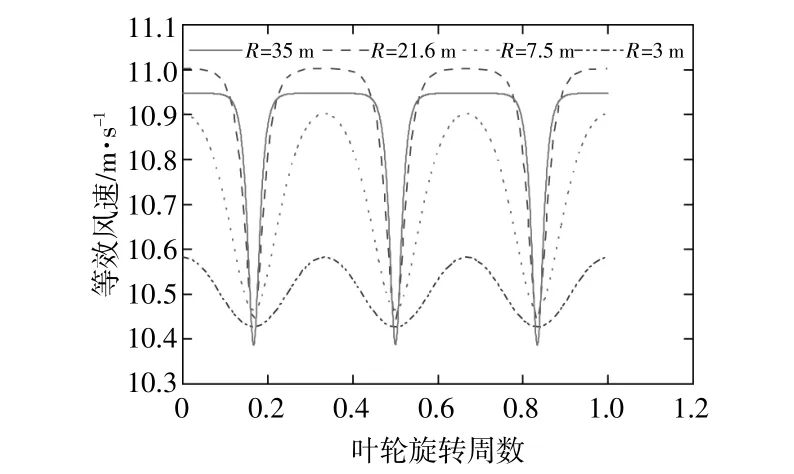
圖1 不同葉輪半徑對應的等效風速曲線Fig.1 Equivalent wind speed curves for different impeller radii

使用MATLAB中的Fourier擬合工具對R=3 m時的風力機等效風速曲線進行擬合，結果見圖2。

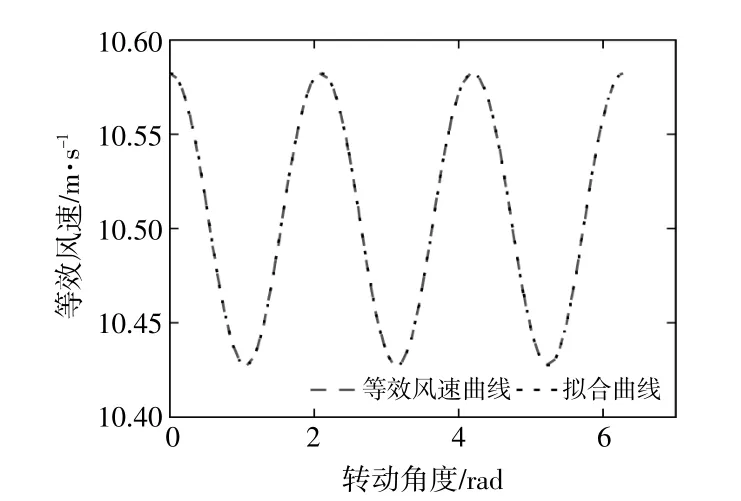
圖2 風速曲線和擬合曲線Fig.2 Wind speed curve and fitted curve

圖2中的擬合曲線表達式見式(9），式(9）中的參數見表1。

表1 擬合曲線參數Table 1 Fitted curve parameters

從圖2可以觀察到擬合曲線與原始風速曲線重合度非常高，a0值接近VH=11，擬合精度為1。其中x=ωYt。

因此，等效風速VE可近似為

式中：ak為風速第k項對應的系數。

2 機組特性分析

根據式(10）以及風力機輸出機械轉矩與風速二次方的正比關系，得到風力機輸出的機械轉矩T為

式中：T0為風機 氣動 轉矩 的穩 態 成 分 ，T0=0.5ρπR3CpV2H/λ；ρ為 空 氣 密 度；Cp為 最 佳 風 能 利用系數；λ為最佳葉尖速比；Tk為轉矩各諧波分量的幅值。

設角速度 ωY對應的頻率為P，由式(11）可知，受等效風速的影響，風力機轉矩也出現3kP的振蕩波動。

雙饋風力發電機的運動方程可表示為

式中：Te為電磁轉矩；ωr為發電機轉子角速度；J為機組的等效轉動慣量。

根據式(12）可以得到雙饋發電機的 ωr。

式中：ωr0為轉子角速度穩態分量。

Ansoft中仿真的風力發電機功率為5.5 kW，葉輪半徑為3 m，設兩對極雙饋發電機轉子以vr=1 000 r/min正常運行，葉輪轉動速度為60 r/min，則ωY=6.28 rad/s。根 據 式(9）～(13），由 表1中 的 風速擬合數據可以求得式(13）中電機角速度的各項附加參數，從而可以得到該轉速下受等效風速影響的發電機波動轉速，利用該波動轉速可以在Ansoft中進行考慮等效風速影響的電機故障研究。

3 氣隙偏心故障的影響分析

本文對動偏心故障下的電磁特性進行分析。雙饋發電機動偏心簡化結構如圖3所示。

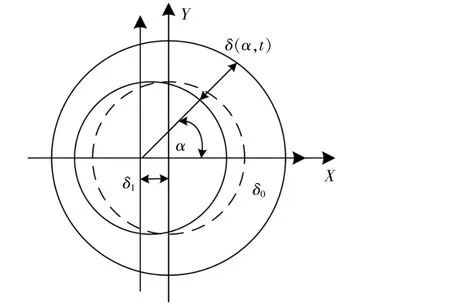
圖3 動偏心簡化示意圖Fig.3 Simplified schematic of a dynamic eccentricity

圖3中，δ1為轉子旋轉中心與轉子幾何中心的距離。以X軸水平方向為起點，得到氣隙δ(α，t）隨時間和轉子轉動位置變化的表達式：

式中：δ0為未偏心的平均氣隙。

根據磁導與氣隙之間的關系，并對其進行冪級數展開，忽略高階分量，可得：

青島中山路歷史街區(以下簡稱中山路街區)位于青島市南區中西部，西鄰青島火車站，南接棧橋公園.創始于1897年的德國占領時期，在改革開放以后逐漸蕭條[1].天主教堂位于中山路的東側山坡臺地之上，塔身高56 m，是整個中山路街區的重要節點，構成中山路歷史街區輪廓線的控制高度[2] (圖1).

式中：μ為真空磁導率；Sδ為有效磁導面積；Λ0為未偏心下氣隙磁導常值成分；Λ1為動偏心成分。

由磁路歐姆定律得到主磁通表達式：

式中：F為磁通勢；ω1為風力發電機旋轉磁場轉速。

動偏心故障下的主磁通表達式中，出現了新的轉速為 ω1±ωr的附加磁場。新的附加磁場將會導致定子繞組中出現對應頻率的定子電流成分[10]。這部分定子電流會與基波磁通互相作用，導致主磁通受到相位調制，使定子電流中出現 ω1±kωr一系列成分。從結果而言，即轉子動偏心故障下，定子電流受到了頻率為轉頻fr的信號調制。

雙饋風力發電機定子直接與電網相連，轉子通過變流器與電網相連。當雙饋發電機轉速變化時，通過變流器調節饋入轉子繞組的電流頻率與相位，保持定子端輸出頻率穩定，即轉子轉頻和轉子勵磁電流頻率之和等于定子電流頻率。

由上述分析可知，等效風速使發電機轉子旋轉頻率中出現了3kP成分，導致轉子繞組中勵磁電流產生相應頻率的波動。為了獲得穩定的機電能量轉換，并使定子與轉子之間的旋轉磁場保持相對靜止，轉子繞組中的諧波又會在定子繞組中感應出對應的諧波。因此，發電機定子繞組中也應存在調制頻率為3kP的磁場分量。

等效風速下電機主磁通可表達為

式中：ck為系數Tk/(3kJωY）在定子中引起的波動系數。

式 中：dk=Tk/(3kJωY）。

引入等效風速后，動偏心故障下發電機主磁通的頻率成分非常復雜，必然導致定子電流成分也發生相應變化。在定子電流頻率中除了基頻 ω1和偏心故障特征頻率 ω1±k1ωr0之外，在這些頻率的附近均會出現3kP的調制邊帶，也即 ω1±3kP和 ω1±ωr0±3kP，以及前兩者進一步相互作用產生的 頻 率 ω1±k1ωr0±3kP。

4 仿真及結果分析

為驗證理論分析的正確性，在Ansoft中搭建了雙饋風力發電機的2D仿真模型，模型結構如圖4所示，參數見表2。

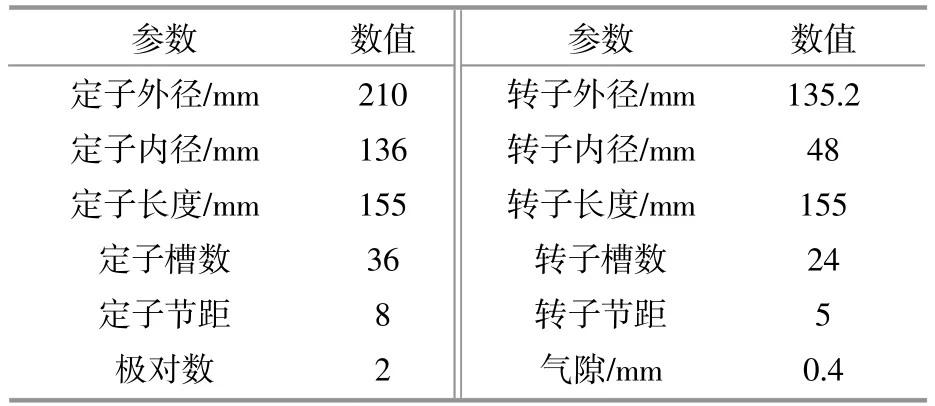
表2 模型參數Table 2 Model parameters

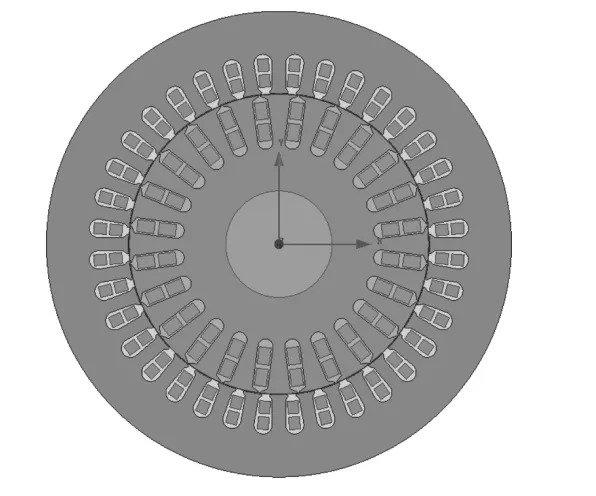
圖4 風力機2D模型Fig.4 2D model of a wind turbine

對該雙饋風力發電機模型分別進行正常工況、動偏心工況和等效風速疊加動偏心工況下的仿真，發電機轉子轉速為1 000 r/mim，采樣頻率為5 kHz。采集定子電流數據，并對結果進行功率譜密度(PSD）分析。正常運行的定子電流頻譜見圖5(a），單獨添加動偏心故障(偏心距離為0.15 mm）情況下的定子電流頻譜如圖5(b）所示。由圖5可知，偏心故障下，定子電流頻率中出現了f±fr和f±2fr成分，符合理論推導中動偏心故障下定子電流新增f±kfr頻率成分。

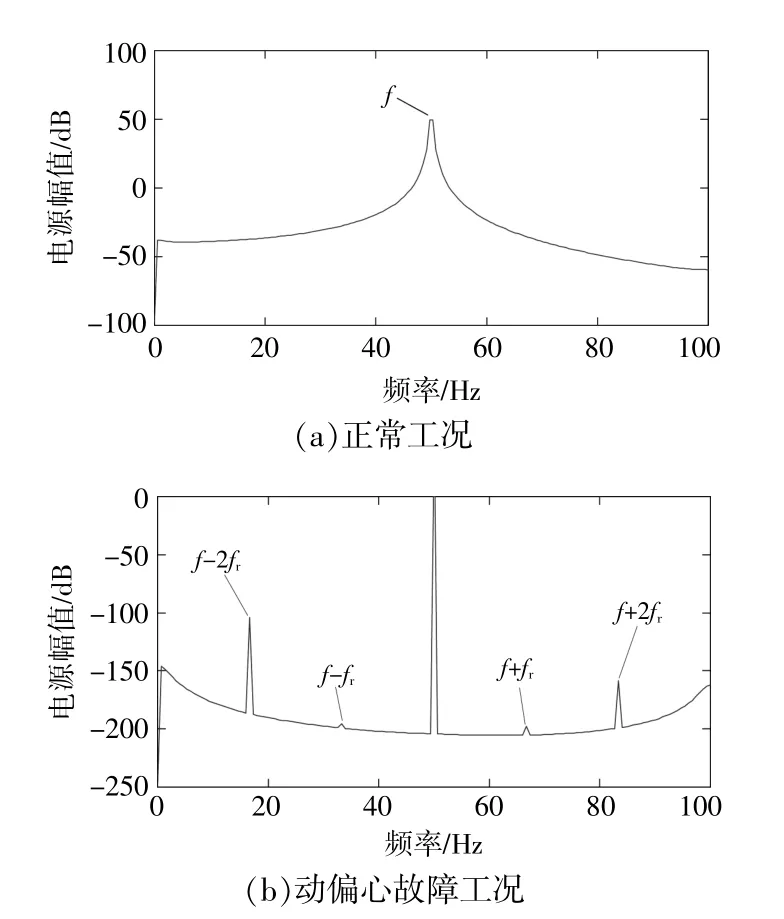
圖5 定子電流PSD譜Fig.5 PSD spectrum of stator current

根據前述理論分析，將轉子轉速設置為受等效風速影響的轉速，然后進行動偏心疊加等效風速工況下的仿真，結果如圖6所示。

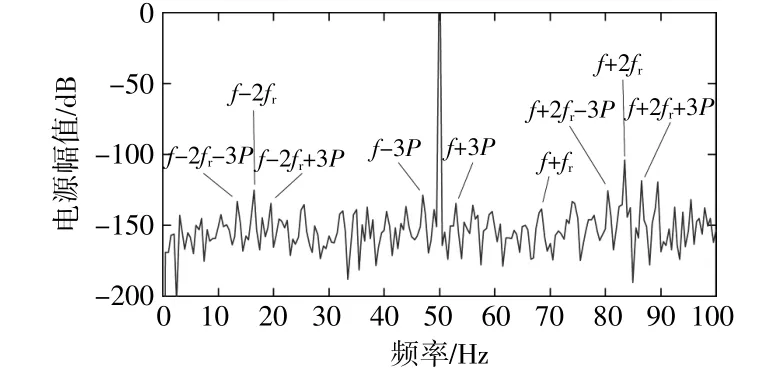
圖6 等效風速影響下的動偏心故障定子電流頻譜(0.15 mm）Fig.6 Dynamic eccentric fault stator current spectrum under the influence of equivalent wind speed(0.15 mm）

由圖6可知，定子電流基頻f附近出現由等效風速引起的f±3kP頻率成分，動偏心故障特征f±2fr頻 率 成 分 十 分 明 顯，且 附 近 出 現f±2fr±3kP的頻率成分，即仿真結果與理論推導一致。在此基礎上，將動偏心增加到0.18 mm，重復實驗，結果如圖7所示。

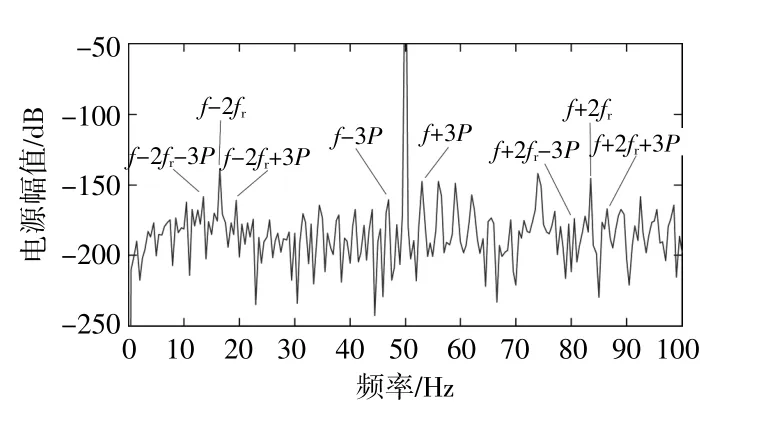
圖7 等效風速影響下的動偏心故障定子電流頻譜(0.18 mm）Fig.7 Dynamic eccentric fault stator current spectrum under the influence of equivalent wind speed(0.18 mm）

為了進一步觀測不同葉輪角速度下等效風速的影響，在0.15 mm偏心故障仿真基礎上，將葉輪角速度設置為之前的一半，即 ωY=3.14 rad/s，轉子轉速不變，重新擬合等效風速，并進行仿真，處理后的結果如圖8所示。

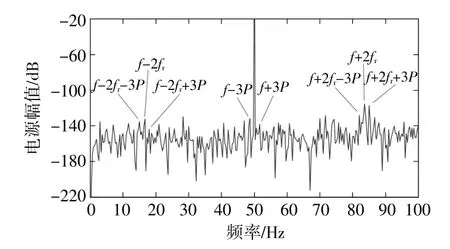
圖8 等效風速影響下的動偏心故障定子電流頻譜(0.15 mm，ωY=3.14 rad/s）Fig.8 Dynamic eccentric fault stator current spectrum under the influence of equivalent wind speed(0.15 mm，ωY=3.14 rad/s）

與圖6相比，圖7中的故障特征頻率成分更為突出，且等效風速所引起的3kP調制邊帶十分明顯。在圖8中，能觀測到動偏心故障特征頻率成分，與圖6相比，橫軸上3P的值明顯減小，等效風速引起的3kP調制邊帶更加密集，符合理論推導。

等效風速和動偏心故障均對發電機主磁通產生了影響，于是導出定子繞組的磁鏈數據，并對其進行處理，繪制其頻譜(圖9）。由圖9可知，在等效風速影響下，動偏心故障的定子繞組磁鏈中出現了較為明顯的動偏心故障頻率成分f+2fr和f+4fr，且這兩個頻率周圍也有3kP的邊帶，與理論推導吻合。

圖9 磁鏈PSD譜Fig.9 Flux PSD spectrum

5 實驗及數據分析

為了更進一步驗證理論推導與仿真的正確性，本文利用雙饋風力發電機實驗臺進行等效風速影響下的轉子動偏心故障實驗。圖10為雙饋發電機及偏心調節裝置，在發電機轉子加長部分切割了一段槽。

圖10 發電機及氣隙偏心故障模擬裝置Fig.10 Generator and the air gap eccentricity fault simulation platform

正常運行時，這段切槽的轉子在發電機定子的外側。需要模擬動偏心故障時，通過圖10所示的螺栓，推動發電機定子，使切槽的轉子進入到定子，模擬定轉子之間的動態氣隙偏心。

本次實驗模擬的 ωY值設定為1.05 rad/s，并在此轉速基礎上生成等效風速曲線。對應的3P值為0.5 Hz，發電機轉子轉頻fr為20 Hz。采樣頻率為10 000 Hz，采樣時間為20 s，將采集的定子電流數據進行處理并繪制頻譜圖(圖11）。由圖11可知：在基頻50 Hz附近出現了因等效風速周期性波動導致的3kP邊帶；圖11(b）中動偏心故障特征頻率f-fr較為明顯，且附近存在一系列3kP成分；圖11(d）中f+fr頻率成分不明顯。

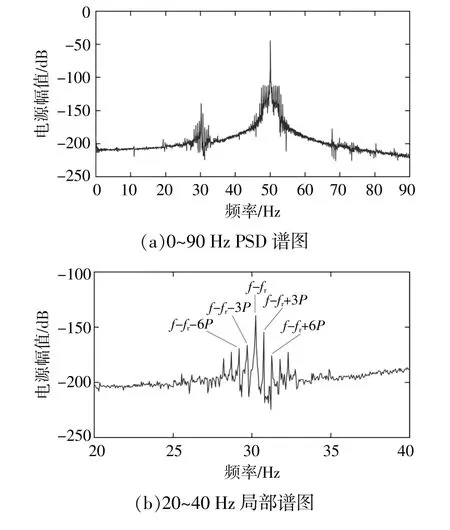
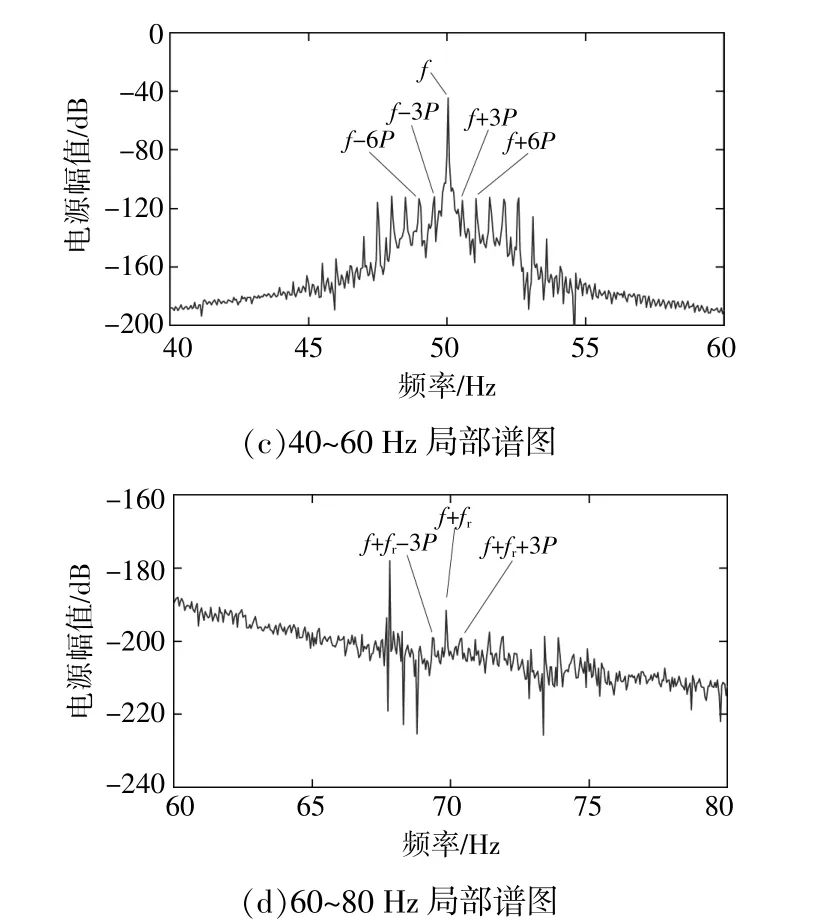
圖11 實驗臺定子電流PSD譜(1.05 rad/s）Fig.11 Stator current PSD spectrum of test rig(1.05 rad/s）

在圖11所示實驗結果的基礎上，又增加一組葉輪角速度ωY為0.525 rad/s的實驗，并重新擬合等效風速。對應的3P值為0.25 Hz，發電機轉子轉頻fr為10 Hz，實驗結果如圖12所示。

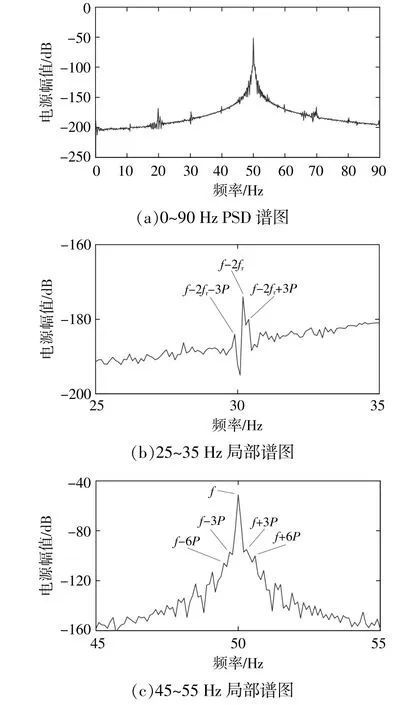
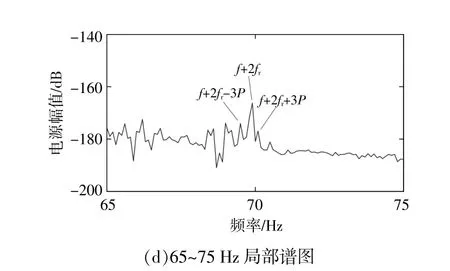
圖12 實驗臺定子電流PSD譜(0.525 rad/s）Fig.12 Stator current PSD spectrum of test rig(0.525 rad/s）

由 圖12可 以 觀 察 到f±fr，f±2fr，f±3fr，以 及 周圍的3P邊頻帶，結果與圖11基本類似。但與圖11相比，隨著葉輪角速度的降低，等效風速所引起的3P數值隨之減小，3kP邊帶也隨之變得更加密集。實驗結果與理論推導和仿真結果吻合。

6 結論

本文從等效風速和雙饋風力發電機組動偏心故障的機理出發，通過理論推導、仿真分析以及實驗驗證，得出以下結論。

①實際風況中的風剪切和塔影效應影響風力機的氣動特性，造成氣動轉矩和轉速波動，并進一步通過傳動部件影響到發電機轉子轉速，導致電機電磁參量發生變化。

②考慮等效風速后，動偏心故障特征發生變化，且比較復雜。在定子電流中，除了定子電流基頻外，還有動偏心特征頻率轉子轉頻、等效風速所引起的3kP調制頻率以及上述頻率的相互耦合產生的新頻率。研究結果為實際工況下的動偏心故障診斷和監測提供了一定的理論依據。