一境二構三問:促進概念教學的深度理解

龔玲　徐良盛

［摘 要］深度理解是小學數學核心素養發展的重要前提。在概念課“倍的認識”教學中創設了一個充滿童趣的教學情境并一以貫之，“從2倍著手到3倍、4倍等更多倍的認識”這一教學明線及“變中有不變”的教學暗線，構建了明暗疊加的雙層次結構化教學，激起了學生思維的火花。在教學難點處的三次追問，將課堂一次次推向高潮，引領著學生的思維步步深入，實現了從具體到抽象、從課堂到生活的雙重教學目標。

［關鍵詞］概念教學；深度理解；情境；結構化；追問

［中圖分類號］ G623.5［文獻標識碼］ A［文章編號］ 1007-9068（2023）29-0040-05

【教學背景】

“倍的認識”是人教版教材三年級上冊第五單元的內容，該內容是在學生已經初步了解了乘法和除法意義的基礎上進行教學的。“倍”是一個重要但相對抽象的概念，與“分數”“百分數”和“比”等概念密切相關，為學生的后續學習提供了基礎。

通過前測發現，班級里大約5%的學生能夠描述倍數關系，但對于倍的確切含義的理解還較為模糊。例如，對于蘋果6個、梨3個這樣的情境，學生能理解蘋果的數量是梨的2倍，但當蘋果和梨的具體數量改變后，有些學生可能感到困惑。這反映部分學生對于“倍”的理解仍然比較表面，還未深入掌握。

基于此，筆者在設計“倍”這一教學內容的教學環節時，有意突出了以下兩點。第一，以“2倍”為切入點，緊緊圍繞這個基本的倍數關系開展教學。通過構建直觀的“倍”模型，幫助學生充分理解“倍”的本質。第二，通過“變中求不變”的方法，逐步引導學生更深入地理解“倍”的含義。教師鼓勵學生從在具體情境中對比逐漸過渡到形式上的對比，同時引導學生通過分析多種具體事物的共性，抽象出事物的數量特征。

【課堂實錄】

一、創設情境，初步認識“倍”

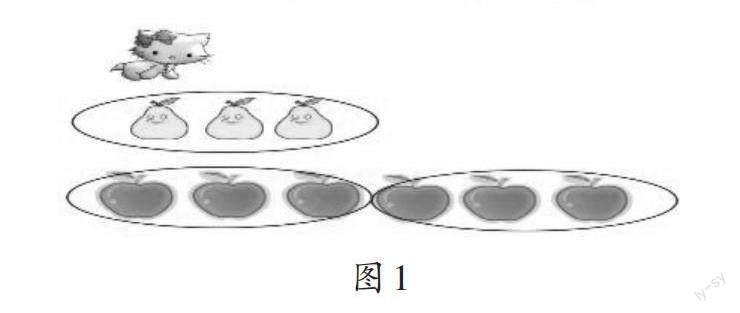
師（出示圖1）：秋天來了，果園豐收了，小動物們忙著摘水果。請仔細觀察，看看能從圖中獲得哪些數學信息？

師：蘋果和梨的個數有怎樣的數量關系？

生1：蘋果比梨多3個。

生2：梨比蘋果少3個。

生3：蘋果的個數是梨的2倍。

師：你是怎么知道蘋果的個數是梨的2倍的？

生3：蘋果有6個，梨有3個，6里面有2個3。

生4：3+3=6。這也能看出6里面有2個3。

師：是的，兩個數量之間，除了“多”和“少”的關系，還有著“倍”的關系。如果我們把3個梨看作一份（邊說邊在黑板上圈），蘋果有這樣的幾份呢？對，有這樣的2份。我們就說，蘋果的個數是梨的2倍。今天我們就要來研究有關“倍”的知識。

【設計解讀：學生喜聞樂見又充滿童趣的“小動物摘水果”的教學情境，能抓住小學低段學生的心理特點，激發學生的好奇心和求知欲。數一數、算一算這些都是學生常用的方法，為后續新知的教學做好了鋪墊。】

二、探究新知，對比中認識“2倍”

1.在變中求不變

師：看！小狗也來摘果了，小狗摘的水果個數有沒有倍數關系呢？（出示圖2）你是怎么想的？

生1：蘋果有4個，草莓有2個，4里面有2個2。

師：誰聽懂了？

生2：如果把2個草莓看作1份，蘋果有這樣的2份，因此，蘋果的個數是草莓的2倍。

師：是的，如果把2個草莓看作1份，蘋果有這樣的2份，我們就說蘋果的個數是草莓的2倍。

師（出示圖3）：小象也來了， 它摘的水果個數又有著怎樣的倍數關系呢？（學生回答略）

師：我們看看三個小動物摘的水果，它們摘的個數一樣嗎？（不一樣）為什么各自摘的兩種水果數量都有2倍關系？

師（將圖4-1的信息隱去，得到圖4-2）：如果把上面的水果看作1份，下面的水果有這樣的幾份？（學生回答略）

師：如果把上面的水果看作1份，下面的水果都有這樣的2份，因此下面的水果個數都是上面的2倍。同學們真會觀察，能從不同中找到相同點，真棒！

【設計解讀：該環節采用圖像表征、操作表征、啟發談話、深度思考、合作交流等形式，引導學生將思考過程用“把（）看作1份，（）有這樣的2份，我們就說（）是（）的2倍”這樣準確、精練的語言表達出來。一系列學生喜愛的“小動物摘水果”的教學情境充分建構“倍”的直觀模型，學生通過觀察思考“在變中求不變”，進一步認識“倍”，教師通過追問“水果個數不一樣，為什么都有‘2倍關系？”引導學生深入理解“倍”的本質。】

2.無序中滲透有序思想

師（出示圖5）：小豬摘的水果看上去有點亂。你能從這么亂的圖中看出倍數關系嗎？你用的是什么辦法？

生3：圈一圈，將4個西瓜看作1份，菠蘿有這樣的2份。（教師出示圖6）

生4：理一理，一一對應重新擺。（教師出示圖7）

生5：也可以列式得“8÷4=2”。

師：你們不僅看到了圖，還從中看到了數；不光看到了數，還看到了數量之間的關系。真棒！

【設計解讀：本環節繼續利用“小動物摘水果”的教學情境，由易到難、從有序到無序，層層遞進。開放的問題情境，激起了學生思維的火花，滿足了不同學生的需求，讓不同層次的學生得到不同的發展。】

三、練習中過渡到“多倍”，完善“倍”的認識

師：剛才我們說了那么多2倍，那么有沒有3倍、4倍甚至更多倍呢？請大家看練習題，找找看兩個數量之間的關系。（出示圖8）

【設計解讀：在學生充分認識了2倍，基本建構了“倍”的模型后，教師通過類比遷移，引導學生自主認識3倍、4倍等多倍關系。】

四、錯例辨析中深入理解“倍”

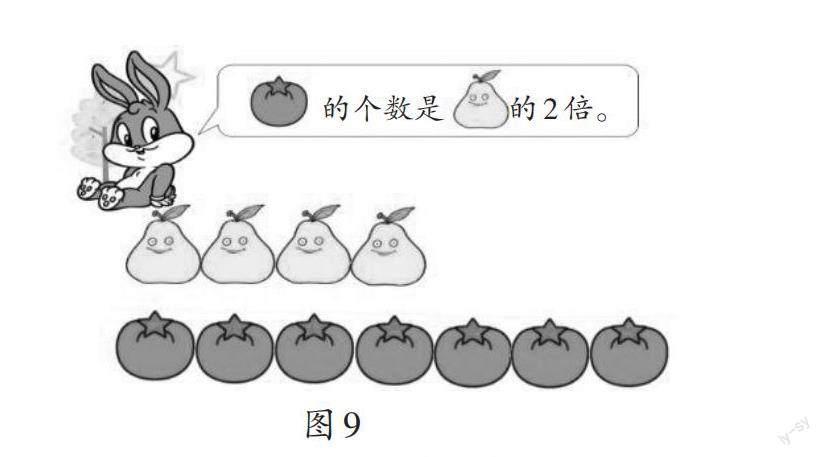
師（出示圖9）：小兔也來湊熱鬧了。小兔說的對嗎？

生1：不對，梨有4個，蘋果只有7個，它們之間不是2倍關系。

師：你分析得很有道理。這里是把什么看作1份？

生2：把4個梨看作1份。

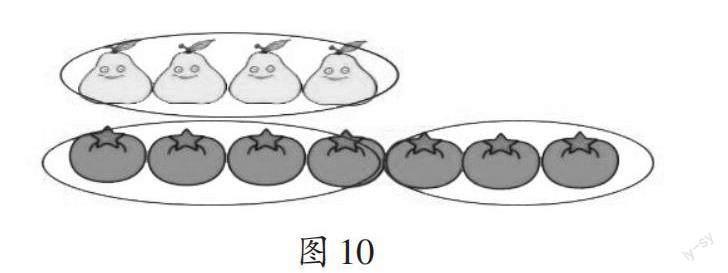
師（出示圖10）：這樣看，柿子算兩份嗎，為什么？

生3：不算，因為下面的其中一份只有3個柿子，必須4個4個地圈，4個為一份，不能隨便圈。

師：把4個梨看作1份，柿子也要4個4個地圈，1份數必須相同。把4個梨看作1份的話，怎么改一改柿子的個數才能讓柿子的個數是梨的2倍？

生4：加1個柿子。

生5：還可以分別去掉1個梨和1個柿子。

師：你的想法很有創意。這樣的話，原來1份數就變成了3個。它們還是2倍關系，即1份數在變，總數也隨之改變。

【設計解讀：在學生面對一系列問題，對于“倍”能正確理解后，設計一道“有問題”的練習引發學生的認知沖突，學生呈現“心求通而未得，口欲言而弗能”的憤悱狀態。此時提供給學生自主嘗試的機會，使學生在暢所欲言中加深對“倍”的理解，同時收獲多種糾錯的方法。特別是學生還提出了“可以分別去掉1個梨和1個柿子”的打破常規的思路， “倍數關系不變，1份數在變，總數也隨之改變”這一結論的提出也水到渠成。心理學家蓋耶曾說過“若不允許學生自主嘗試和犯錯，就將錯過最富有成效的學習時刻”，的確如此！】

五、操作中感受比的標準，認識“1倍”

師（出示圖11-1）：果園的柿子可多啦，小狗和小兔又來了。小兔想知道她摘的個數是小狗的幾倍。小兔摘了幾個？你們發現了什么？哦，小狗摘的個數不知道。那你們猜一猜，小狗有可能摘了幾個？有幾種可能？每一種情況中，小兔摘的個數是小狗的幾倍？先獨立探究，然后完成下面練習（如圖11-2）。

師：什么情況下是1倍的關系呢？

生1：當兩個數量一樣時。

師：為什么小兔摘的個數一直沒有變，而這里的倍數關系卻在不斷地變化呢？

生2：因為小狗摘的個數在變，也就是1份數在變化，所以倍數關系也會隨之改變。

【設計解讀：這是一道開放題，倍數關系不是獨立存在的。小兔摘了12個，小狗摘的個數不知道，那么小狗摘的個數和12存在倍數關系的情況就有多種。而題中“ 摘的個數是 的（ ）倍”，實則是求“12是（ ）的（ ）倍”，也就是大數是小數的幾倍。學生很容易得出1、2、3、4、6、12與12的倍數關系，其中難度較大的是1倍和12倍。當小狗摘的個數是12個，也就是和小兔摘的一樣多時，小兔摘的個數是小狗的1倍；當小狗只摘了1個時，小兔摘的個數是小狗的12倍。此題的教學意義不僅是讓學生理解“1倍”，隨著問題“為什么小兔摘的個數一直沒有變，而這里的倍數關系卻在不斷地變化呢？”的提出，學生的思維進入了更深處。】

六、游戲：翻一翻，變中再次感受比的標準

師：小貓咪摘水果累了，想和小朋友們玩個游戲。這里總共有12個白圓（出示圖12-1），老師把其中一個翻了過來，瞧，它變成了黑圓（出示圖12-2）。這時白圓有幾個？（11個）黑圓呢？（1個）。你能用一句話說一說白圓的個數和黑圓的個數之間的倍數關系嗎？

生1：11白、1黑，白圓的個數是黑圓的11倍。

師：再翻一個呢？請說出其中的倍數關系。

生2：10白、2黑，白圓的個數是黑圓的5倍。

師：如果再翻一個呢？

生3：9白、3黑，白圓是黑圓的3倍。

師：再翻一個呢？

生4：8白、4黑，白圓是黑圓的2倍。

師：猜一猜，接下來還可以怎么翻？誰愿意來翻一下？

……

師：為什么前面我們說“白圓是黑圓的幾倍”，現在卻變成了“黑圓是白圓的幾倍”呢？

生5：因為黑圓個數比白圓的多了。

生6：前面我們是把黑圓看作1份，白圓有這樣的幾份，就是黑圓的幾倍；隨著黑圓個數越來越多，我們把少的白圓看作1份，黑圓有這樣的幾份，我們就說黑圓是白圓的幾倍。

師：不難發現，比的標準不一樣，倍數關系也會隨之變化。

【設計解讀：教學接近尾聲，高潮沒有落幕。游戲環節再次激起學生思維的火花，課堂氛圍活躍，學生沉浸在快樂而有深度的學習中。隨著白圓不斷減少、黑圓不斷增加，比較的標準發生了變化，倍數關系也會隨之變化。從“倍數關系不變，1份數在變，總數也隨之改變”到“1份數在變，倍數關系隨之改變”，再到“比較的標準發生了變化，倍數關系也會隨之變化”，真正實現了教學的“三進階”。】

七、回歸生活，全課總結

師：同學們在生活中遇到過倍數關系嗎？“把（ ）看作一份，（ ）有這樣的（ ）份，我們就說，（ ）是（ ）的（ ）倍。”你能像這樣說一說生活中遇到的倍數關系嗎？

生1：弟弟有5支鉛筆，我有10支鉛筆，我的鉛筆支數是弟弟的2倍。

生2：我有10本書，同桌有50本書，同桌的書本數是我的5倍。

生3：我們學校三年級有8個班，四年級也有8個班，三年級的班級數是四年級的1倍，也可以說四年級的班級數是三年級的1倍。

師：同學們真是生活的有心人，能舉出來這么多關于倍數的例子。的確，有幾個1份數這么多，我們就說它與1份數之間存在幾倍的數量關系。

師：今天我們認識了“倍”這個新朋友，你知道了關于“倍”的哪些知識呢？（學生回答略）同學們，祝賀你們成功走進了“倍”的世界，感悟到了數學是源于生活，并應用于生活的。我們將在生活中繼續探索更多有關“倍”的知識！

【教學反思】

本節課遵從課程標準要求，精準把握學情，透徹分析教材，將教學內容趣味化、結構化、懸疑式，以培養學生建構“倍”概念這一模型的基本推理意識和推理能力。本課例主要有以下特點。

一、趣味化創設教學情境

正如于漪老師所說，“課的第一錘要敲在學生的心靈上，激發起他們思維的火花”。的確，好的開頭可如磁石一般能將學生牢牢吸引。本節課圍繞“小動物摘水果”這一教學情境開展“倍”的認識教學，并且這一情境貫穿始終，符合學生身心發展特點，充滿童趣又高潮迭起的課堂牢牢吸引了學生的注意力。

二、結構化梳理教學重點

本節課從重點突破“2倍”入手，引導學生初步理解“倍”的概念，再類比遷移到3倍、4倍及更多倍的學習——這是一條教學的明線; 從“倍數關系不變，1份數在變，總數隨之改變”到“總數不變，1份數在變，倍數關系隨之改變”，再到“比較的標準發生變化，倍數關系也會隨之變化”，變中有不變——這是一條教學的暗線。皮亞杰指出：“數學是對結構的構建而建立起來的。”明暗疊加的雙層次結構化教學設計，將教學步步引向深入。

除此之外，構建“倍”的教學模型過程中，教學板書的結構化為有效突破教學難點提供了有力保障。教師帶著學生在圈圈畫畫中打造了簡潔明了、重點突出的板書，有力地引導學生不僅“想得通”，更要“說得清”，將內在思維外化為語言輸出，為突破語言表達這一教學目標提供了強有力的“腳手架”。與此同時，在課的最后，教師利用此板書（如圖13-1、13-2），將學生的視域從有限的課內數學轉移到了廣闊的生活數學，實現了從具體到抽象，從課堂到生活的雙重教學目標。

三、懸疑式追問教學難點

教學中，教師的主要任務在于“引”，而學生的主要任務在于“思”。本節課教師在教學難點處的三次追問，將學生的思維步步引向深入。教師的問，問在了教學內容的難點處，問在了學生思維的盲點處。只有教師有的放矢、“撥開迷霧”地追問，才能讓學生體會到抽絲剝繭、漸入佳境的“豁然開朗”，學生對“倍”概念的深度理解才能一步步實現！

任何一種教育理念都只有根植于課堂實踐這片肥沃的土壤才會具有鮮活的生命力。基于深度理解的教學設計不僅符合認知負荷理論，也是數學智慧課堂的必然選擇。這種設計有助于學生深入理解和系統掌握知識，同時感悟到學習內容所體現的思維方法。唯有教師深度理解的教學實踐才能促進學生的深度理解真正發生；唯有教師自身在教學上深入思考，才能引領學生的思維進入更深處！

［ 參 考 文 獻 ］

[1] 劉加霞.從加法結構到乘法結構：“倍”是轉折點：評析高麗杰老師的“倍的初步認識”[J].小學教學，2010（Z1）：17-19.

[2] 安富海.促進深度學習的課堂教學策略研究[J].課程·教材·教法，2014，31（11）：57-62.

[3] 劉月霞，郭華.深度學習：走向核心素養[M].北京：教育科學出版社，2018.

（責編 金 鈴）