基于田口法和遺傳算法的取向硅鋼片直線電機優化設計

高子晏,董 婷

(沈陽工業大學 電氣工程學院,沈陽 110870)

0 引 言

在工業機器人、軍工和航空航天等領域,對電機的體積、推力密度和定位精度等指標要求十分苛刻,希望電機做到輕量化的同時,具有短時高過載能力[1-3]。取向硅鋼片的磁性能與軋制方向密切相關,多應用于變壓器鐵心且只應用高磁導率的軋制方向[4]。文獻[5]采用取向硅鋼片制作永磁同步電機定子,利用其軋制方向高磁導率的特點,緩解了電機定子齒部的飽和程度,提高了電機的功率密度。文獻[6]利用取向硅鋼片構建了拼接齒結構的永磁力矩電機,提高了電機的轉矩密度和過載能力。文獻[7]利用取向硅鋼片降低了電機的鐵耗,提高了電機的效率和輸出轉矩。旋轉電機應用取向硅鋼片多采用拼接或榫卯結構,這會提高電機的制造成本和制作難度。

近年來,電機多目標優化逐漸向代理模型結合優化算法方向發展。文獻[8]采用Pearson相關系數對各優化變量進行分層,基于Kriging模型和NSGA II對各層參數進行多目標優化,降低了電機的轉矩脈動和損耗。文獻[9]基于田口法對組合磁極永磁同步電機的轉矩與懸浮力進行快速尋優。文獻[10]結合響應面法和遺傳算法對圓筒型永磁直線電機進行多目標優化,提高了電機的綜合性能指標。田口法可以提高尋優效率但全局尋優能力較差,遺傳算法全局優化能力強但存在早熟收斂導致無法尋得全局最優的問題。結合田口法和遺傳算法可以充分發揮兩者的優勢,具有更好的多目標優化效果。

本文介紹了取向硅鋼片直線電機的結構特征,構建了該電機的磁網絡模型,結合該模型以電磁推力、推力波動和永磁體利用率為優化目標,研究了一種基于靈敏度分析的分層優化方法。針對顯著優化變量,結合田口法與遺傳算法進行多目標優化,普通優化變量則采取單參數掃描法,針對長行程和高推力密度兩種應用場合分別給出了兩種最優方案。

1 取向硅鋼片直線電機磁網絡模型

1.1 取向硅鋼片直線電機

以一臺傳統永磁直線同步電機為例,將其初級鐵心替換為取向硅鋼片,作為取向硅鋼片直線電機的初始方案,圖1為30P120型取向硅鋼片和DW465-50型無取向硅鋼片的磁導率-磁通密度曲線,表1為直線電機初始方案的結構參數。

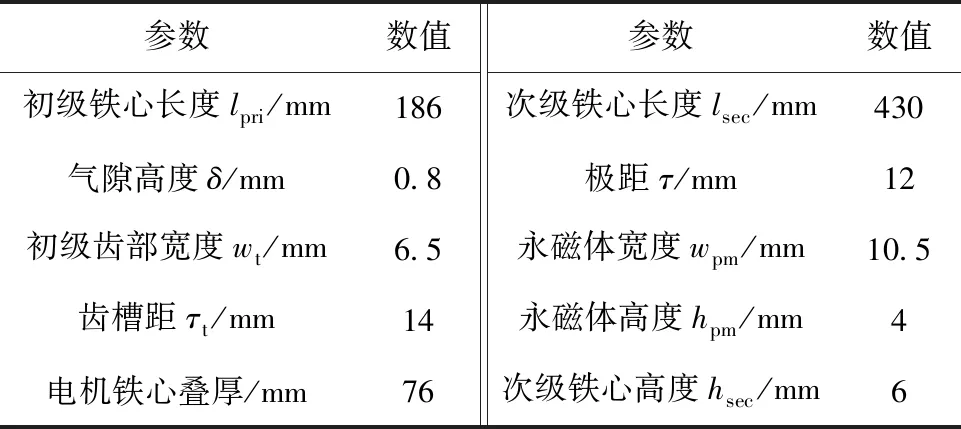
表1 12槽14極直線電機初始方案結構參數

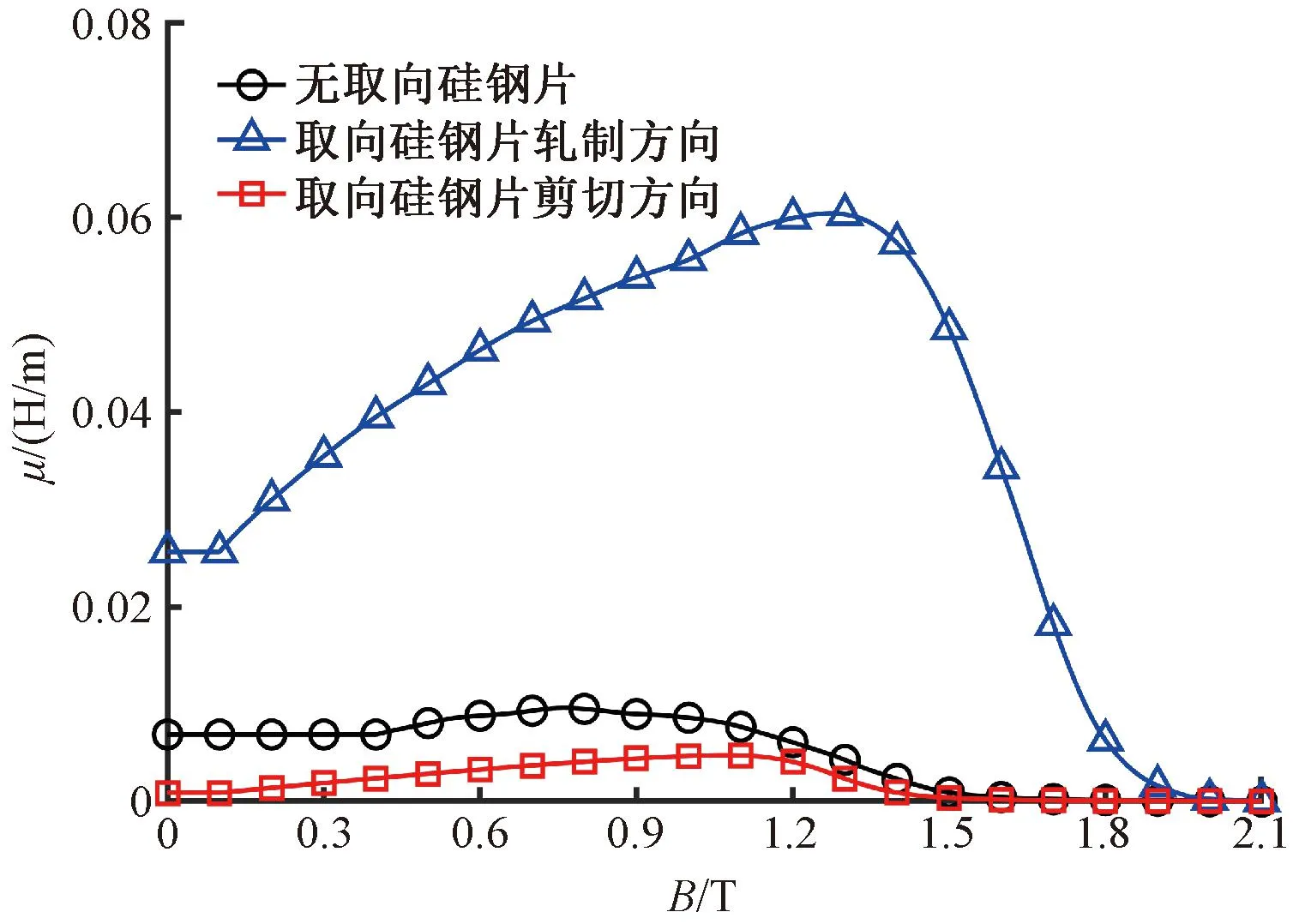
圖1 磁導率-磁通密度曲線

將取向硅鋼片軋制方向與直線電機齒部主磁通方向保持一致,其軋制方向磁導率更高,剪切方向與軛部磁路方向相對應,取向硅鋼片直線電機拓撲結構如圖2所示。近極槽直線電機的軛部磁路較短,即使取向硅鋼片剪切方向的導磁能力不佳,對直線電機性能的影響仍然很小。本文直線電機額定負載電流為4.5 A,圖3為兩種材料直線電機推力-電流曲線。取向硅鋼片直線電機相比傳統直線電機,在額定負載和3倍過載情況下推力分別提升4.03%和8.13%。

圖2 取向硅鋼片直線電機拓撲結構

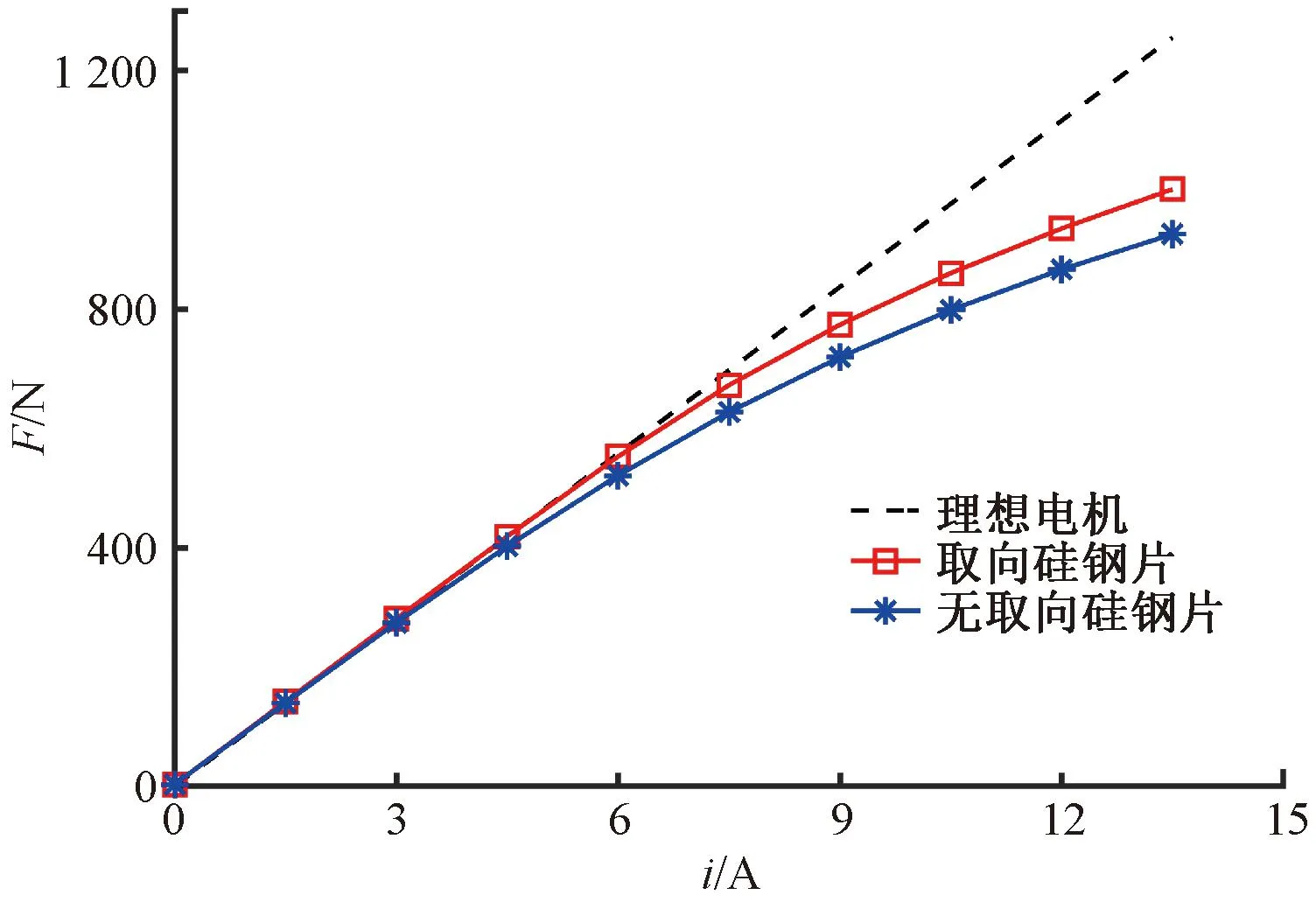
圖3 推力-電流曲線

1.2 磁網絡模型

結合取向硅鋼片直線電機的拓撲結構和磁通路徑構建磁網絡模型,其電樞和永磁體磁動勢:

(1)

式中:N為電樞繞組匝數;i為電樞電流;hpm為永磁體高度;HC為永磁體矯頑力。

應用積分計算各支路磁阻,直線電機磁網絡模型中磁阻多為矩形,其計算公式如下:

(2)

式中:hcom為元件寬度;μ0和μr為真空磁導率和相對磁導率;wcom為元件寬度;lef為鐵心有效長度。

直線電機初級齒軛連接處各向異性磁阻:

(3)

式中:μt和μy為軋制方向和剪切方向磁導率;θ為與軋制方向的夾角。

本文構建的取向硅鋼片直線電機磁網絡模型如圖4所示。有限元法計算耗時30 min,磁網絡法用時45 s。有限元法和磁網絡法求解的A相空載與負載反電動勢和推力對比如圖5和圖6所示。兩種方法的反電動勢計算結果基本吻合,兩種方法的推力計算結果為418.61 N和425.86 N,偏差為1.73%。

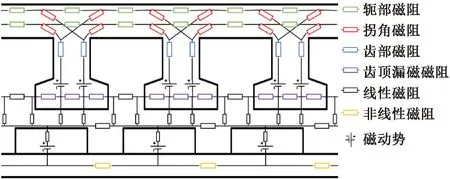
圖4 取向硅鋼片直線電機磁網絡模型

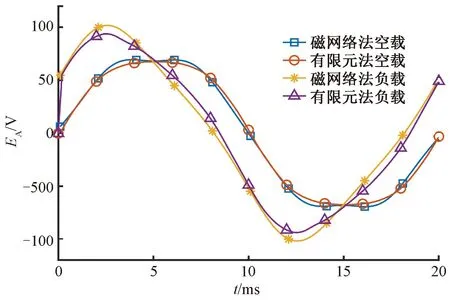
圖5 A相空載和負載反電動勢對比

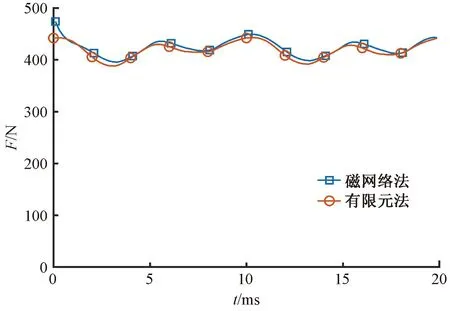
圖6 額定負載推力

基于磁網絡模型求解直線電機的電磁特性相較于有限元法偏差在5%以內,驗證了所構建模型的正確性,為后續直線電機的深度優化奠定了基礎。

2 電機結構參數的靈敏度分析

直線電機的多目標優化屬于高維多物理場耦合問題,某些優化參數與優化目標之間存在交叉耦合,部分參數則較為獨立且影響較小。如果對所有優化參數均采用優化算法,會使工作量呈指數增加,降低直線電機的優化效率。因此,需要根據靈敏度分析對優化參數進行分層,針對綜合靈敏度大于0.3的顯著優化變量,采用田口法結合遺傳算法進行多目標尋優,普通優化變量則采用單參數掃描法優化,進而獲得取向硅鋼片直線電機的最優設計方案。直線電機的多目標優化流程如圖7所示。基于磁網絡模型確定優化參數的變化范圍并對其進行靈敏度分析,后續采用有限元法進行深度優化。

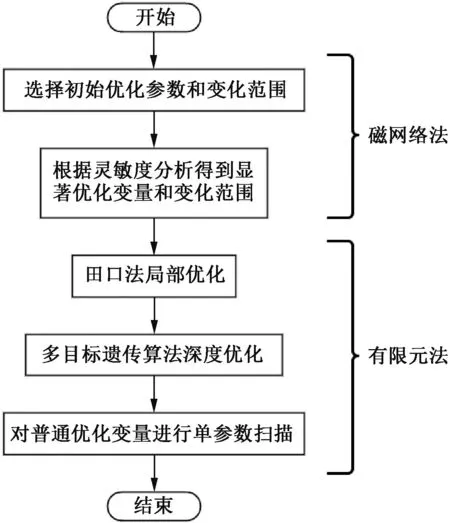
圖7 磁網絡法聯合有限元法優化流程

選出直線電機合適的初始優化參數,通過磁網絡模型確定各優化參數合理的變化范圍,保持電流密度不變,J≈5 A/mm2,在槽面積變化時改變槽中繞組匝數,保證槽滿率相同,sf≈0.7,電負荷與銅耗隨每槽導體數變化。表2給出了8個初始優化參數及其變化范圍。

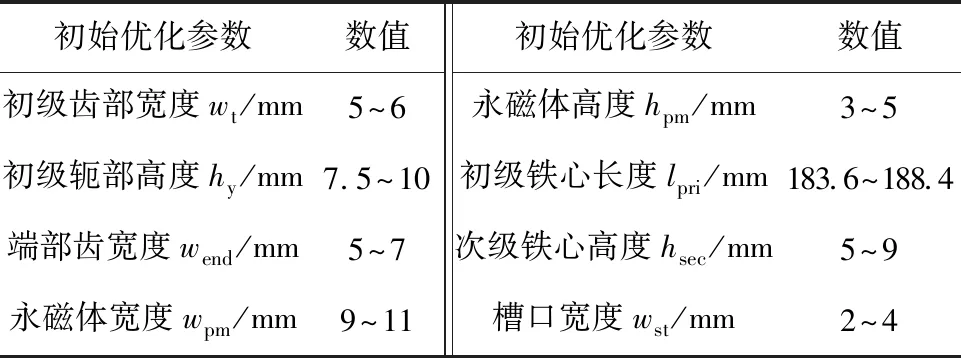
表2 初始優化參數和變化范圍

初級鐵心長度的改變體現在端部槽寬度的變化,初級鐵心長度發生變化時端部齒寬度保持不變。端部齒寬度發生變化時初級鐵心長度保持不變,改變端部槽寬度。選擇取向硅鋼片直線電機的電磁推力、推力波動和永磁體利用率作為優化目標,其目標函數:

(4)

式中:F′ave、F′rip和F′den表示初始模型取向硅鋼片直線電機的電磁推力、推力波動和永磁體利用率;σ1、σ2、σ3為權重系數,滿足σ1+σ2+σ3=1;Fave(n)、Frip(n)和Fden(n)表示當優化參數為n時,所對應的優化目標數值。

取向硅鋼片直線電機更適用于高推力密度場合,因此電磁推力是考慮的重點;降低推力波動可以提高直線伺服系統的控制性能;隨著行程的增加,永磁體用量較大會帶來成本的激增,應合理利用永磁材料。因此,電磁推力和推力波動的權重系數σ1和σ2別取0.5和0.3,永磁體利用率的權重系數σ3為0.2。

永磁體利用率為電磁推力與單塊永磁體截面的比值:

(5)

利用磁網絡模型計算取向硅鋼片直線電機的電磁性能,對優化參數進行靈敏度分析:

(6)

式中:Fi(n)為當優化參數取值為n時優化目標i的數值;Fi為優化目標i的初始值。

引入權重系數得到優化參數的綜合靈敏度:

S(n)=σ1|save(n)|+σ2|srip(n)|+σ3|sden(n)|

(7)

式中:save、srip和sden分別為優化參數對應優化目標的靈敏度。

圖8和表3為8個初始優化參數對應優化目標的靈敏度和綜合靈敏度。初級齒部寬度wt、永磁體寬度wpm、永磁體高度hpm和初級鐵心長度lpri的綜合靈敏度較高,均大于0.3;齒部寬度和永磁體參數對電磁推力和永磁體利用率的影響較大,wt、hpm和lpri對推力波動有較大的影響。

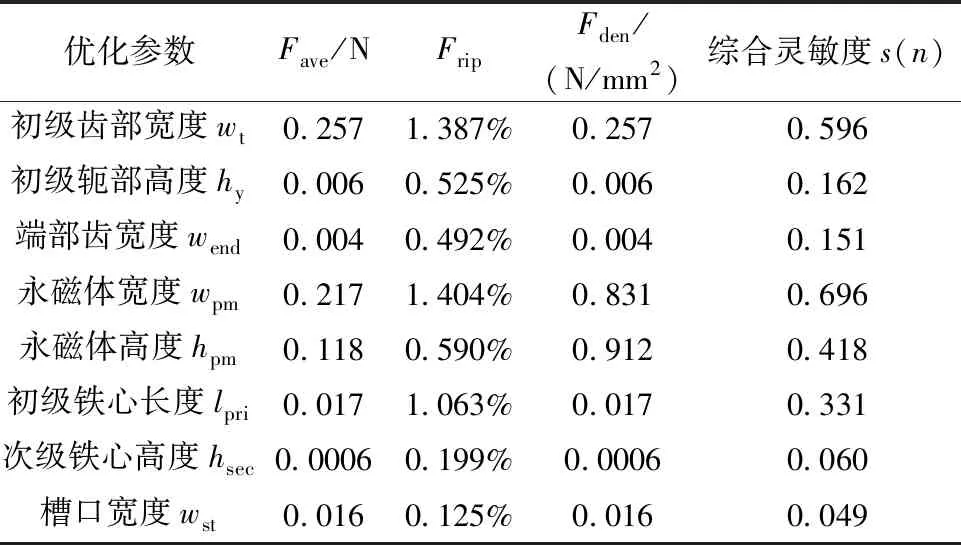
表3 優化參數的靈敏度分析結果

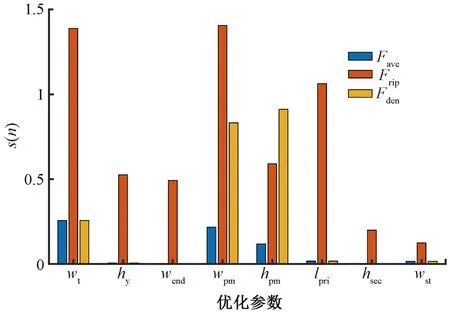
圖8 優化參數的靈敏度分析

綜上所述,選取wt、wpm、hpm和lpri為顯著優化變量,采用優化算法進行深度優化;軛部高度hy、槽口寬度wst、次級鐵心高度hsec和端部齒寬度wend作為普通優化變量,僅采用單參數掃描法進行優化。

各顯著優化變量對應目標函數的函數值如圖9所示。函數值大于1說明該結構參數下的電機綜合性能更優異。為了盡可能提高取向硅鋼片直線電機的性能,并提升多目標優化效率,根據圖9針對性選取優化變量的取值范圍,其中初級齒部寬度wt為5.2～5.5 mm,初級鐵心長度lpri為186～189.6 mm,永磁體寬度wpm為10～10.9 mm,永磁體高度hpm為3.1～4 mm,利于田口法尋取最優參數組合。

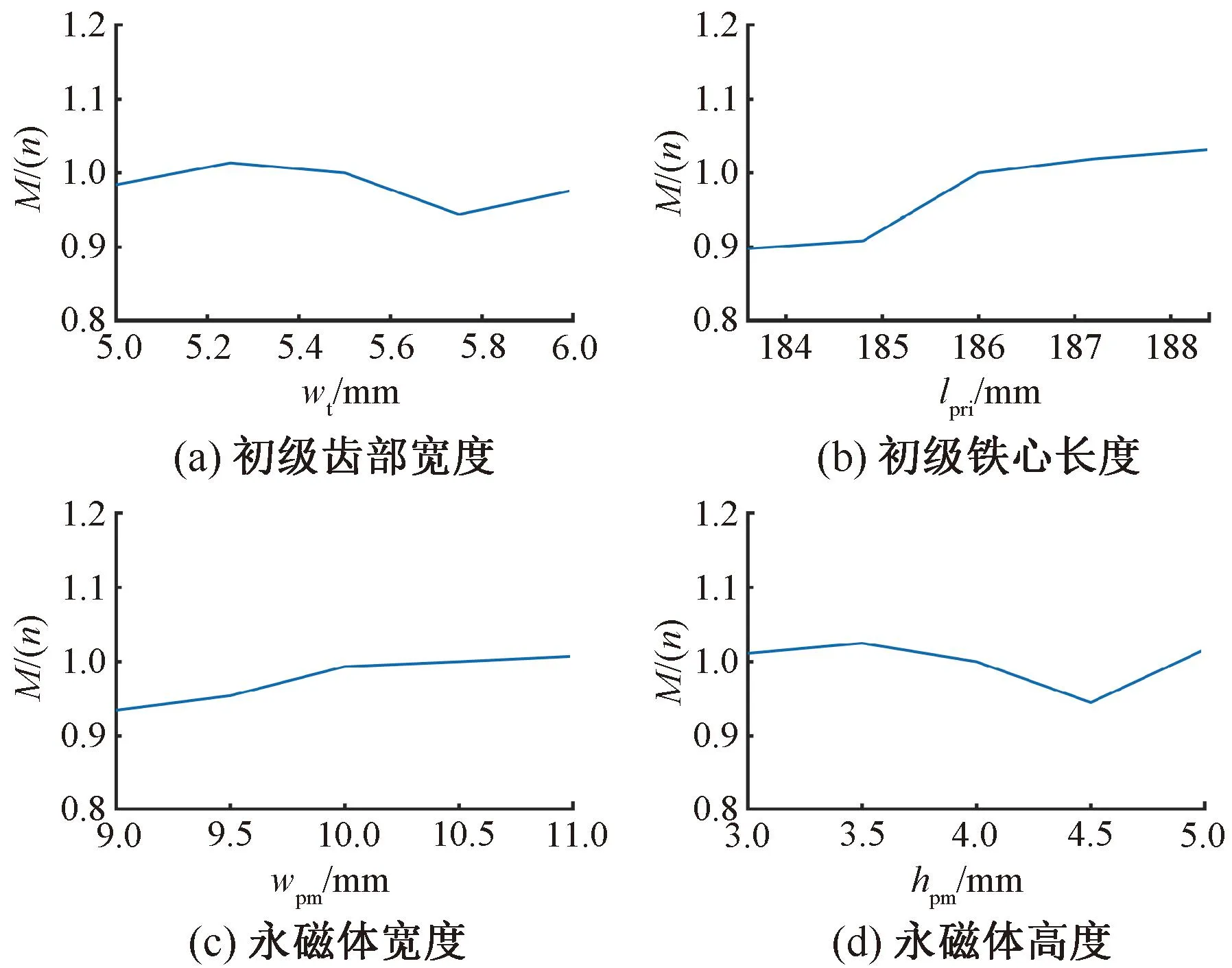
圖9 顯著優化變量與目標函數關系

3 基于田口法的優化設計

基于上一節對各優化參數的靈敏度分析和對優化變量取值范圍的優化,將顯著優化變量作為田口正交試驗的因數,各顯著優化變量及其水平數如表4所示。根據表5,采用田口正交矩陣僅需構建16組試驗方案的仿真模型。基于有限元法計算各組試驗的優化目標數值,根據優化變量的平均值、方差和比重選取田口法的最優方案。圖10為各優化變量對優化目標的影響趨勢。

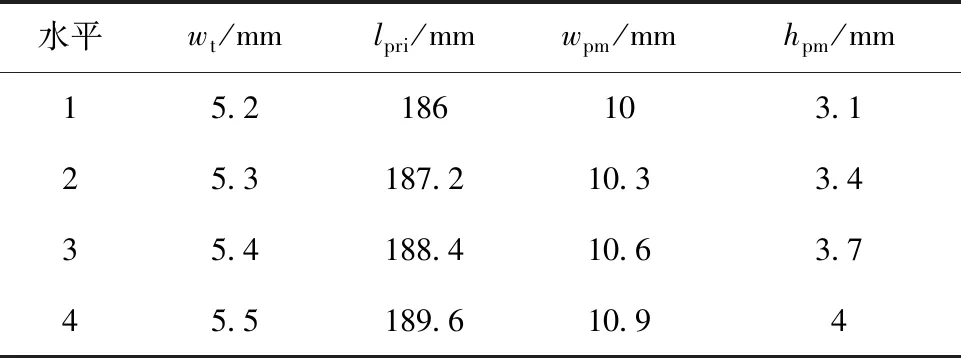
表4 優化變量及水平數

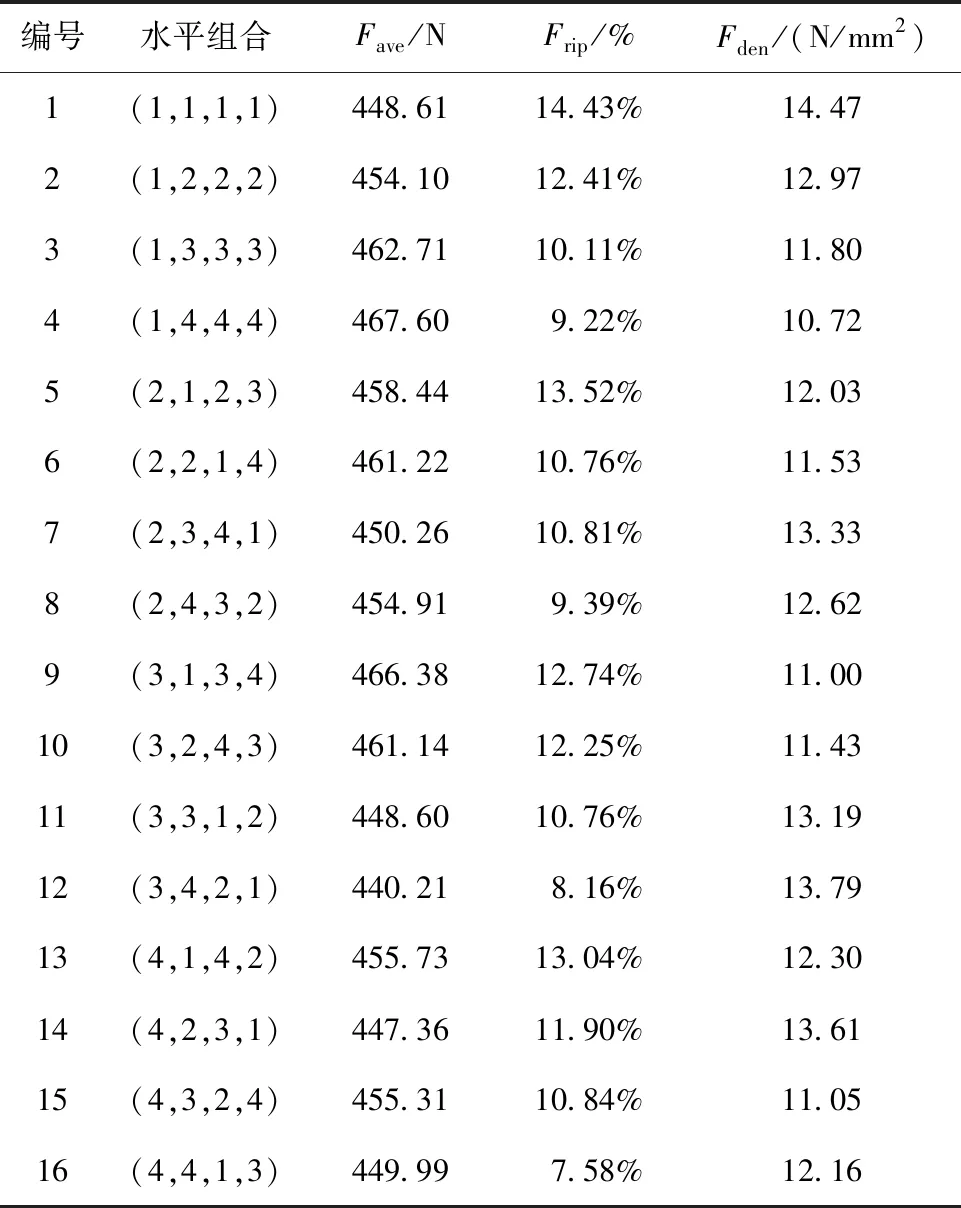
表5 田口正交試驗矩陣L16(44)

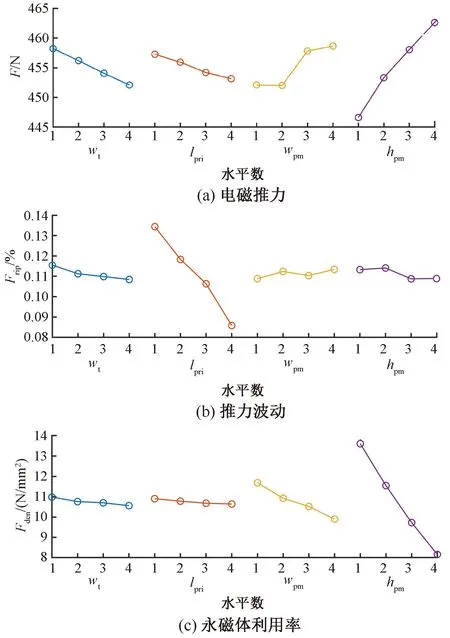
圖10 優化變量對性能指標的影響

方差可以反映一組數據各樣本點偏離總平均值的程度,優化變量方差的計算公式:

(8)

式中:Fia為優化目標i的總平均值。

取向硅鋼片直線電機各優化變量對應優化目標的比重如圖11和表6所示。

表6 優化變量的方差和比重

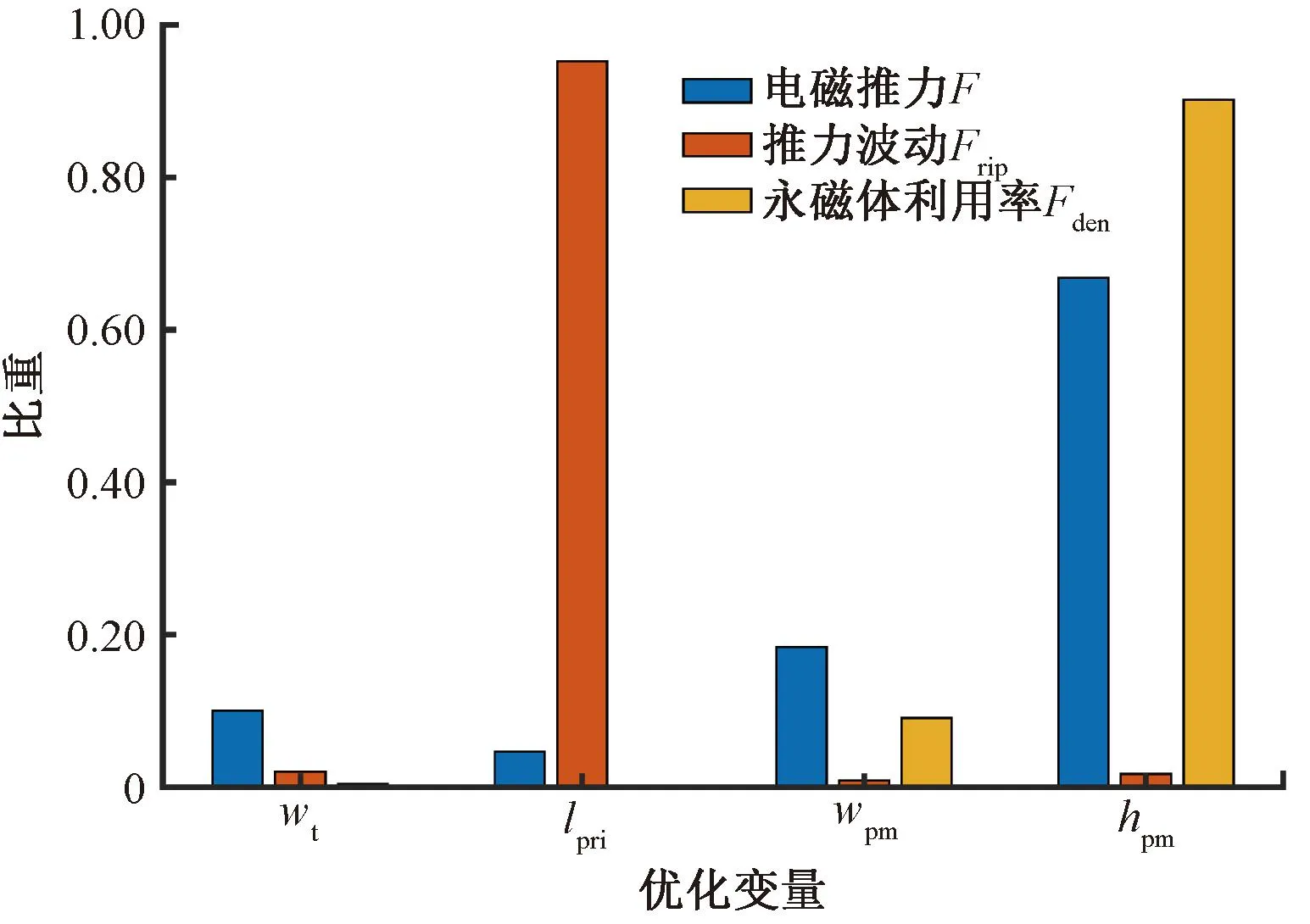
圖11 優化變量對應優化目標的比重

根據方差分析和比重分析,wt對電磁推力的影響最大,lpri對推力波動的影響最大,wpm對電磁推力的影響最大,hpm對永磁體利用率的影響最大。選擇優化變量比重最大的優化目標對應的最優水平參數,田口法的最優方案為wt(1) ,lpri(4),wpm(4),hpm(1),初始方案與田口法結構參數對比如表7所示,優化后電機的初級鐵心長度略微增加。

表7 田口法優化方案結構參數對比

由圖10可知,wpm和hpm對電磁推力和永磁體利用率兩個優化目標的作用趨勢截然相反。田口法的優化原理為將多目標優化簡化為多個單目標優化,基于該方法對取向硅鋼片直線電機進行多目標優化存在弊端,無法全面考慮各優化目標之間的耦合矛盾關系。

4 基于遺傳算法的優化設計

取向硅鋼片直線電機的優化目標之間存在拮抗關系,采用田口法優化電機并沒有實現多優化目標的解耦。遺傳算法具有高效的全局搜索能力,可以解決取向硅鋼片直線電機多目標優化中各優化目標相互制約的問題。將田口法各方案的計算結果作為遺傳算法的初始種群,替代隨機生成的初始種群,可以為遺傳算法的全局優化提供參考。

基于上一節田口法的優化結果和各優化變量的比重分析,針對性選取顯著優化變量的變化范圍,可以減少優化變量的樣本空間,提高優化效率,使優化算法快速向最優參數組合收斂。遺傳算法參數取值如表8所示,以取向硅鋼片直線電機初始方案為基準,對優化目標進行約束:

(9)

表8 遺傳算法參數設置

基于遺傳算法的取向硅鋼片直線電機優化結果如圖12所示。由圖12可知,電磁推力與永磁體利用率近乎呈反比關系,針對不同工程實際需求,在Pareto最優解集中選取方案,本質為在不同優化目標之間折衷。由于遺傳算法優化變量的參數值為隨機生成,考慮到實際加工的可行性,構建尺寸數據僅保留小數點后一位的有限元模型,新有限元仿真結果與遺傳算法理論最優方案可能存在差距。

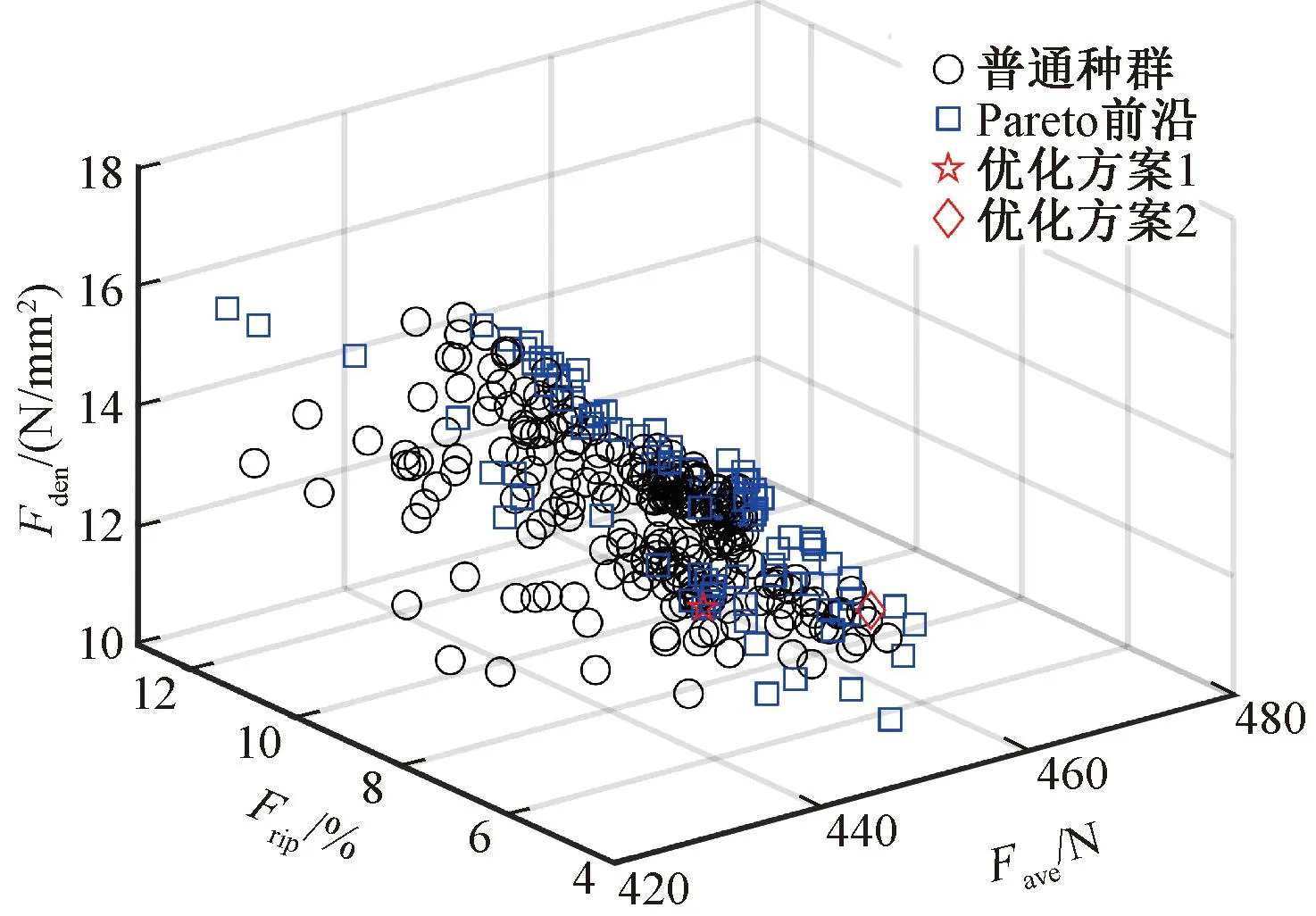
圖12 取向硅鋼片直線電機三維Pareto前沿

以式(4)目標函數值最大為最終優化目標,在Pareto前沿中選取優化方案1,為了方便對比分析遺傳算法的優化效果,在Pareto前沿中選取永磁體結構參數與初始方案相似的優化方案2作為對照組,兩方案的結構參數如表9所示。優化方案1的結構參數與田口法優化結果相似,進一步驗證了田口法優化的有效性。

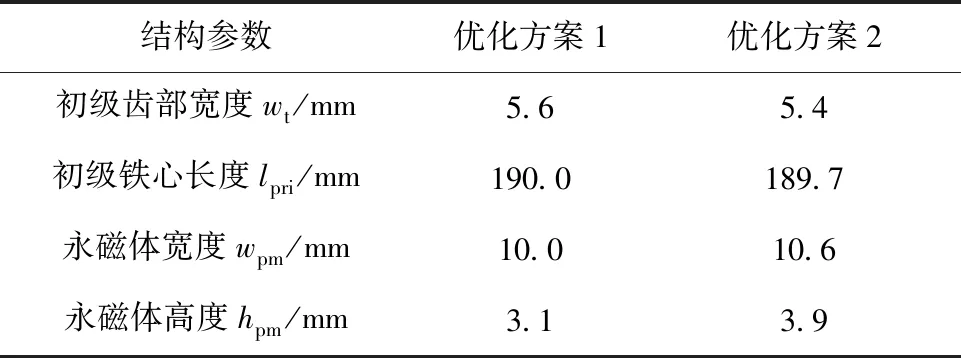
表9 遺傳算法優化方案結構參數

在基于田口法和遺傳算法對顯著優化變量進行多目標優化的基礎上,對普通優化變量采取單參數掃描法尋優,由表3的靈敏度分析結果可知,wy、wst、hsec和wend對直線電機的電磁推力和永磁體利用率的影響較低,相比之下對推力波動的靈敏度大于0.1。因此,以推力波動最小為優化目標,對4個普通優化變量采取單參數掃描法優化,推力波動的優化結果如圖13所示。

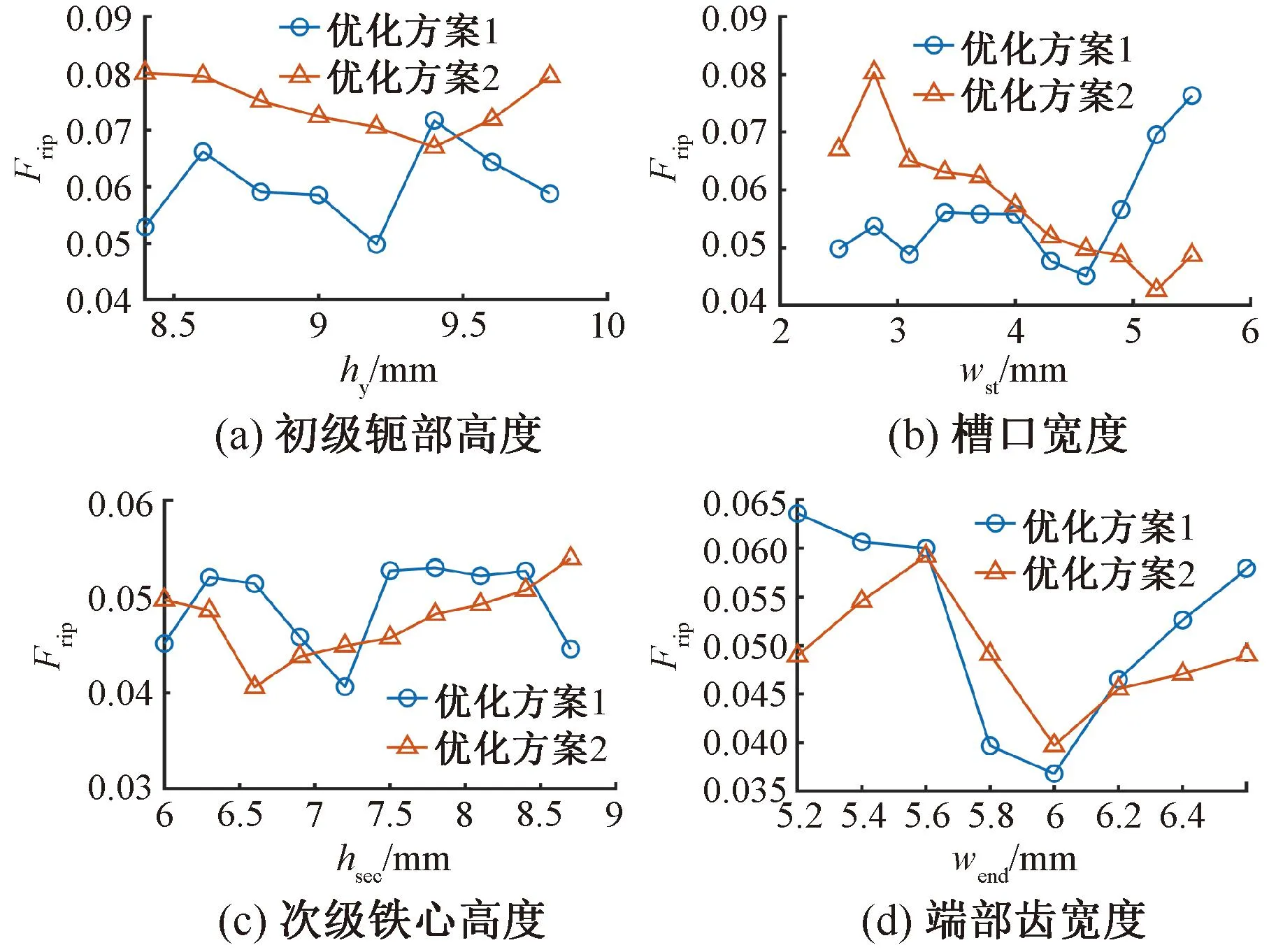
圖13 單參數掃描法優化結果

由圖13可知,普通優化變量對推力波動的影響呈現非線性,根據圖13中推力波動最小值,選取普通優化變量的參數值,結合前文顯著優化變量優化結果,得到最終優化方案如表10所示。田口法、優化方案1和優化方案2的初級鐵心長度相比初始方案都略有增加,3個優化方案的初級齒部寬度wt相比初始方案都有所降低,直線電機的電負荷與銅耗增加。

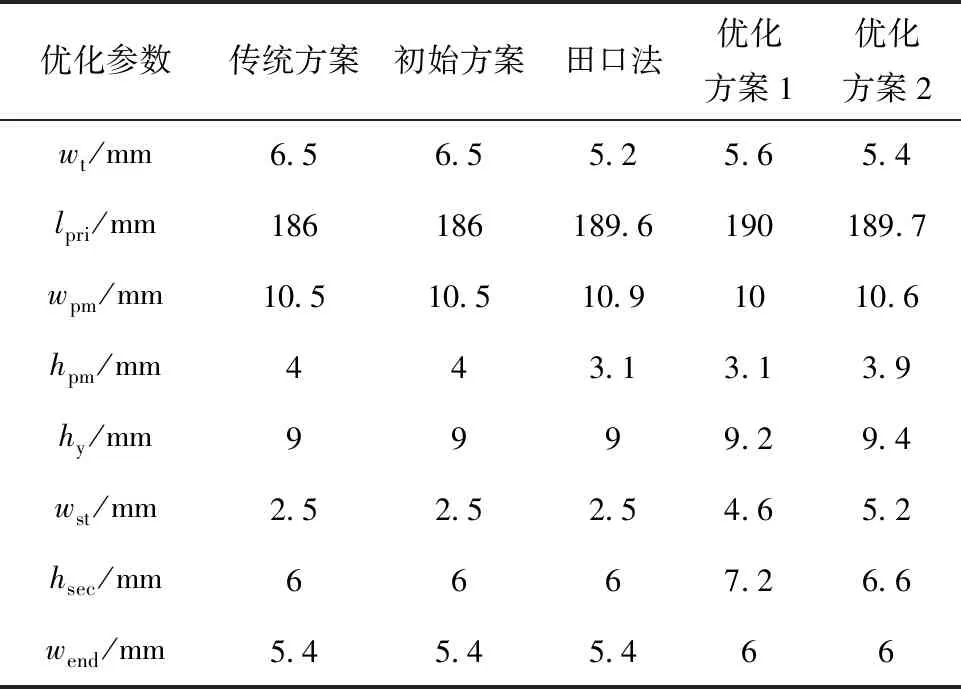
表10 最終優化方案對比

無取向、取向硅鋼片直線電機電磁性能對比如圖14和表11所示。由表11可知,優化方案1和優化方案2的推力波動都低于4%。優化方案1的電磁推力為432.09 N,相比田口法降低了3.96%,但推力波動僅為3.73%,相較田口法下降了55.01%,其永磁體利用率在5種方案中最高,永磁體用量相比田口法降低了8.26%,更適合應用于長行程直線電機,可以有效降低直線電機的制造成本。優化方案2的永磁體用量與初始方案接近,其電磁推力為456.12 N,相較于初始方案提高8.96%,相比傳統直線電機提升13.35%,其永磁體利用率相比初始方案提升了10.63%,該方案更適合應用于對推力密度要求較高的場合。

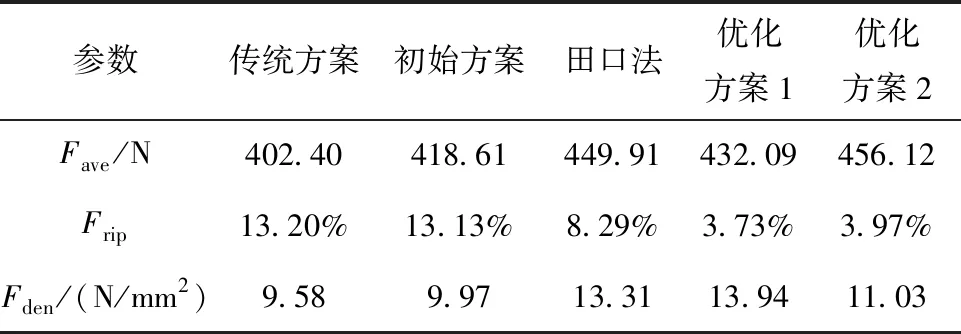
表11 優化結果電磁性能對比

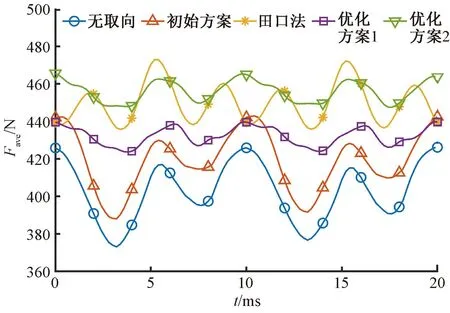
圖14 優化結果對比

結果表明,基于靈敏度分析,采用田口法結合遺傳算法和單參數掃描法對各優化變量進行分層優化的方法,可以有效提高取向硅鋼片直線電機的電磁性能,各優化方案的綜合性能指標均高于初始方案。

5 結 語

本文以一臺12槽14極傳統永磁直線同步電機為例,介紹了取向硅鋼片直線電機的拓撲結構。基于該電機的磁網絡模型,通過靈敏度分析對優化參數進行分層優化,得到以下結論:

1)取向硅鋼片直線電機可以提升直線電機的推力密度。

2)磁網絡模型求解電機的電磁性能相較于有限元法偏差在5%以內,有效降低了計算的時間成本,為取向硅鋼片直線電機的設計和優化奠定了基礎。

3)采用田口法結合遺傳算法和單參數掃描法對各優化變量進行分層優化,可以有效提高取向硅鋼片直線電機的綜合性能指標。通過改變本文目標函數的權重系數,可以根據實際應用需求選取最優方案,為工程實踐提供參考。