最值問題教學“三步走”:建模、運用與變式

作者簡介:殷成葉(1981—),本科學歷,一級教師,從事初中數學教育教學工作.
[摘 要] 中考幾何最值問題是各地熱點考題,學校備課組在復習備考期間都會加強對這類問題的復習研究.如果能將一些同類的最值問題“集中”在一起,根據由易到難、由特殊到一般的邏輯順序展開教學,并注重預設“啟發式問題”促進學生自主發現思路,這樣做不但能讓學生掌握一類最值問題的解答策略,還可以促進學生明辨形異質同的同類問題,發展學生的數學思維.
[關鍵詞] 幾何最值問題;微專題教學;形異質同;啟發式問題
中考幾何最值問題是各地中考試卷中的熱點問題,如何開展這類問題專題訓練與復習備課,成為不少學校備課組集體備課的一個重要課題. 在最近一次集體備課活動中,筆者承擔了一節中考幾何最值微專題的主備任務,經過全組教師的交流討論,最后打磨成一節具有特例引路、變式鞏固、拓展挑戰的幾何最值微專題課例. 本文整理該課教學設計,并給出教學立意的闡釋,提供研討.
教學環節1:特例出發,積累模型
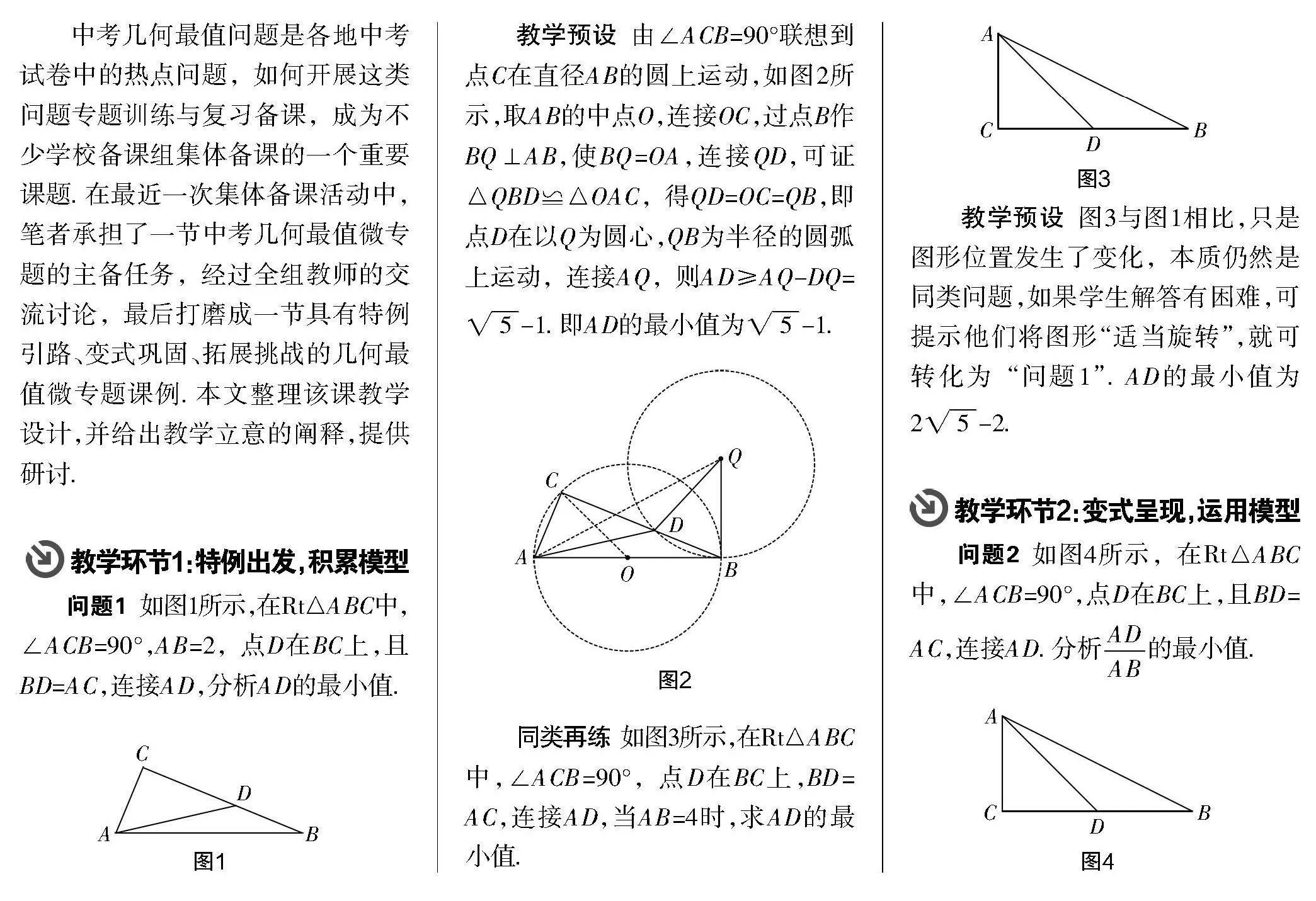
問題1 如圖1所示,在Rt△ABC中,∠ACB=90°,AB=2,點D在BC上,且BD=AC,連接AD,分析AD的最小值.
教學預設 由∠ACB=90°聯想到點C在直徑AB的圓上運動,如圖2所示,取AB的中點O,連接OC,過點B作BQ⊥AB,使BQ=OA,連接QD,可證△QBD≌△OAC,得QD=OC=QB,即點D在以Q為圓心,QB為半徑的圓弧上運動,連接AQ,則AD≥AQ-DQ=-1. 即AD的最小值為-1.
同類再練 如圖3所示,在Rt△ABC中,∠ACB=90°,點D在BC上,BD=AC,連接AD,當AB=4時,求AD的最小值.
教學預設 圖3與圖1相比,只是圖形位置發生了變化,本質仍然是同類問題,如果學生解答有困難,可提示他們將圖形“適當旋轉”,就可轉化為“問題1”. AD的最小值為2-2.
教學環節2:變式呈現,運用模型
問題2 如圖4所示,在Rt△ABC中,∠ACB=90°,點D在BC上,且BD=AC,連接AD. 分析的最小值.
教學預設 與“問題1”相比,本題沒有提供三角形的邊長,待求中,分子、分母都是“變量”,讓我們先“控制”其中一個變量AB. 取AB中點O,連接OC,過B點作BQ⊥AB,使QB=AO,連接DQ,由“問題1”的分析經驗,不妨設AB=2c,AO=BQ=DQ=c,ADS7gZyTGyvAlSkBR/cgX8lNHZj4zeAytupS26tBLnAsg=≥AQ-DQ=(-1)c. 于是AD的最值為(-1)c. 即的最小值為.
同類再練 如圖6所示,四邊形ABCD是正方形,點P在直線AD上,連接BP,CP. 分析的最小值.
教學預設 如果學生感覺有困難,預設如圖7所示的圖形位置,用虛線隱去正方形,補出垂線段PH,可發現PH=BC,這樣問題就轉化為圖4、圖5的“結構”,分析的最小值仍然是.
教學環節3:走向一般,成果擴大
問題3 如圖8所示,在△ABC中,BC=2,∠A=60°,在AC上有一點D,且CD=AB,連接BD,分析BD最小值.
教學預設 首先聯想到△ABC的外接圓,如圖9所示,設它的圓心為P,連接AP,BP,CP,可得∠BPC=2∠BAC=120°,所以BP=PC=2,過C作CO⊥BC,使OC=PB,連接OD,導角得到∠OCD=∠PBA,這樣可證△OCD≌△PBA(SAS),于是OD=PA=PB=PC=2,在Rt△BCO中,BO=4,由BD+DO≥BO,可得BD的最小值為2.
變式 如圖10所示,在△ABC中,BC=2,∠A=60°,在邊AC上有一點D,且CD=AB,連接BD,分析BD的最小值.
教學預設 思路與“問題3”類似,只是構造出的△OCD∽△PBA,相似比為,這樣在Rt△BCO中,BO=,由BD+DO≥BO,可得BD的最小值為-1.
成果擴大 如圖11所示,在△ABC中,BC=a,∠BAC=θ,在邊AC上有一點D,且BD=k·AB,連接BD,分析BD的最小值(用含a,k,θ的式子表示).
教學預設 與前面“特例圖形”的思路類似,構造如圖12所示分析,BP=,OC=k·BP,OB2=BC2+OC2=BC2
+1,進一步可求出BD=OB-OD=(-k).
教學環節4:課堂小結,布置作業
小結問題1 本課研究的系列問題中,前后都有一定的關聯,你是如何理解它們之間的聯系的?舉例說說.
小結問題2 你對本課中哪道問題印象較深?你能否對它做一些變式,提出一個同類問題,并讓你的同桌說說解題的思路?
布置作業 在△ABC中,AB=4,∠C=60°,在邊BC上有一點P,且BP=AC,連接AP,分析AP的最小值.
解法預設 構造如圖13所示,△PBO∽△CAK,則∠CAB=30°+∠CAK,∠ABC=90°-∠CAB,OP=OB=AK=2,∠ABO=∠ABC+∠PBO=90°,AO=2,AP≥AO-PO=2-2.
對于微專題教學,教師要重視同類問題的研究,要促進學生辨明“形異質同”,要善于預設“啟發式問題”.

